基于LMI的空间站角动量管理控制器多级设计*

王梦菲 张 军 李金哲

1.北京控制工程研究所，北京 100190 2.空间智能控制技术国家级重点实验室，北京100190

空间站长期在轨飞行时，采用控制力矩陀螺(Control Moment Gyros, CMGs)作为姿态控制的执行机构。由于其大质量、大惯量的特点，长期飞行时无法像普通卫星一样利用磁力矩器进行CMGs的角动量卸载，而需要借助空间环境力矩进行系统的角动量卸载；同时CMGs还要进行空间站的姿态控制。在轨运行时，这2个任务是同时完成的，从而导致了空间站这种大型组合体航天器所特有的姿态控制和角动量管理(Attitude Control and Momentum Management, ACMM)问题[1-2]。

目前国内外对于空间站姿态控制和动量管理方面已有不少研究成果。Wie等解耦空间站姿态，引入滤波状态量并采用线性二次型调节器(Linear Quadratic Regulator, LQR)设计控制器，减小了由气动力矩引起的空间站姿态和CMG角动量振荡[3]；Sunkel等基于矩阵符号函数，将高维系统分解成块解耦较低维子系统，再利用循环次优LQR算法设计控制器，将极点配置在扇形开区域内[4]；Harduvel等基于三轴耦合模型，引入滤波状态量将原系统扩维，利用传统的LQR算法设计了一种ACMM控制器，能有选择性地抑制姿态或动量状态中恒定或周期性干扰，这种算法在国际空间站中得到了应用[5]；Elgersma等利用μ分析技术评估了H∞控制算法和简化控制补偿器设计方法(内环姿态控制和外环动量管理)对于系统惯量变化的鲁棒性[6]；倪茂林等对于线性不确定系统提出一种具有二次性能指标的鲁棒稳定控制器设计方法，对某型空间站的俯仰动力学控制系统进行了鲁棒设计并取得了较好的控制效果，但需要冗余的CMG且被控对象维数较低，反馈增益阵求解相对容易[7]；李新峰等建立了轨道系下的空间站线性化动力学模型，在Sunkel等提出的解耦算法基础上还考虑了空间站特有的干扰特性，通过带极点配置的LQR方法将闭环极点配置在扇形区域内，但未考虑系统不确定性[8]。

通过上述文献可以看到，ACMM控制对象是高维的多输入多输出系统，传统上多采用LQR方法，但LQR方法面临着加权矩阵选择的问题，一般靠试凑来获得加权阵，通过设计与仿真的反复迭代以达到满意的控制效果，矩阵的选取缺乏理论依据。大型航天器系统控制维数高，控制状态变量中的姿态角和角速度与系统角动量在数值量级上相差能达到5个量级以上，采用LQR方法一次性进行控制器设计时，还常常会导致数值计算奇异问题[4,9]。

针对上述传统方法遇到的问题，本文提出一种新的控制器设计方法，通过线性矩阵不等式(Linear Matrix Inequality, LMI)描述系统期望的极点配置区域，同时满足不确定系统一定的鲁棒稳定要求；通过求解LMI问题得到控制器，避免了传统LQR方法中加权矩阵的选择，弥补了带极点配置的LQR方法由于分步设计而导致极点难以配置在指定梯形区域的不足；通过符号矩阵和求解Lyapunov方程将原系统解耦为维数较低的子系统，经过多步设计实现极点的逐步配置，避免高维矩阵求解中的数值奇异问题。

1 系统模型

1.1 动力学模型

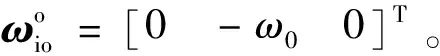
(1)

(2)

(3)

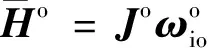
(4)

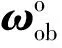
(5)

CMG动力学可表示为：

(6)

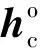
(7)

(8)

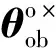
在小角度情况下，从体坐标系oxbybzb内的转动惯量Jb到Jo的转换可近似为：

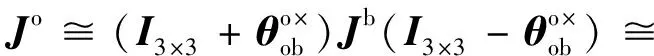
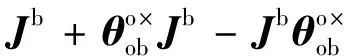
(9)

(10)

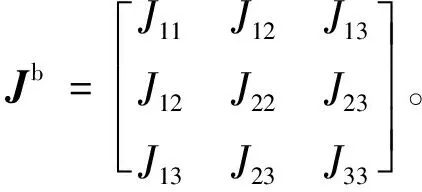
(11)

式中：常值Ai(i=0,1,2)为由三轴分量构成的向量。

重力梯度力矩为：

(12)

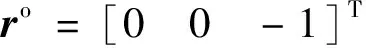
将式(9)代入式(12)得：

(13)

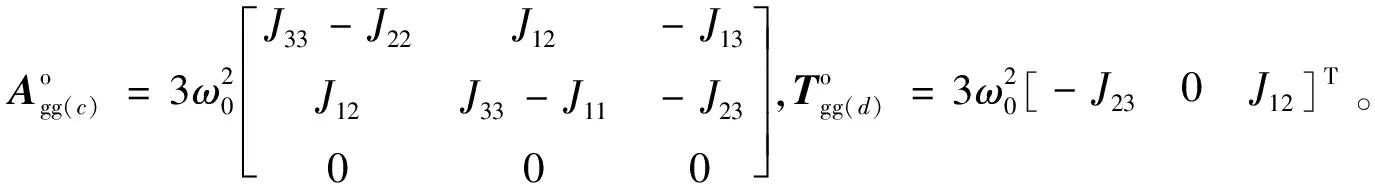
由式(2)、(4)和(13)得如下动力学方程：

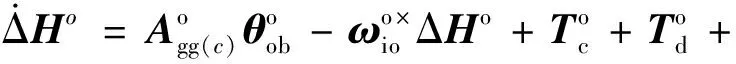
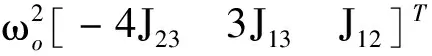
(14)

将式(5)、(7)和(9)代入式(8)并忽略小量高阶项得到如下运动学方程：

(15)

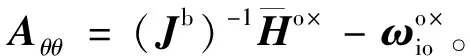
联合式(6)、(14)和(15)，得到线性化的 ACMM 状态空间模型为：

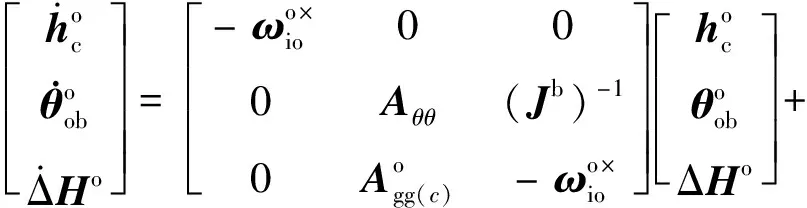
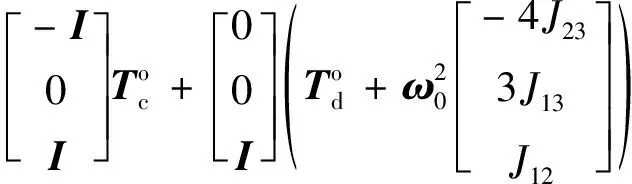
(16)

1.2 基于内模原理的控制模型

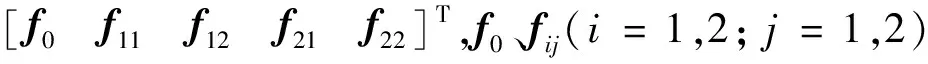
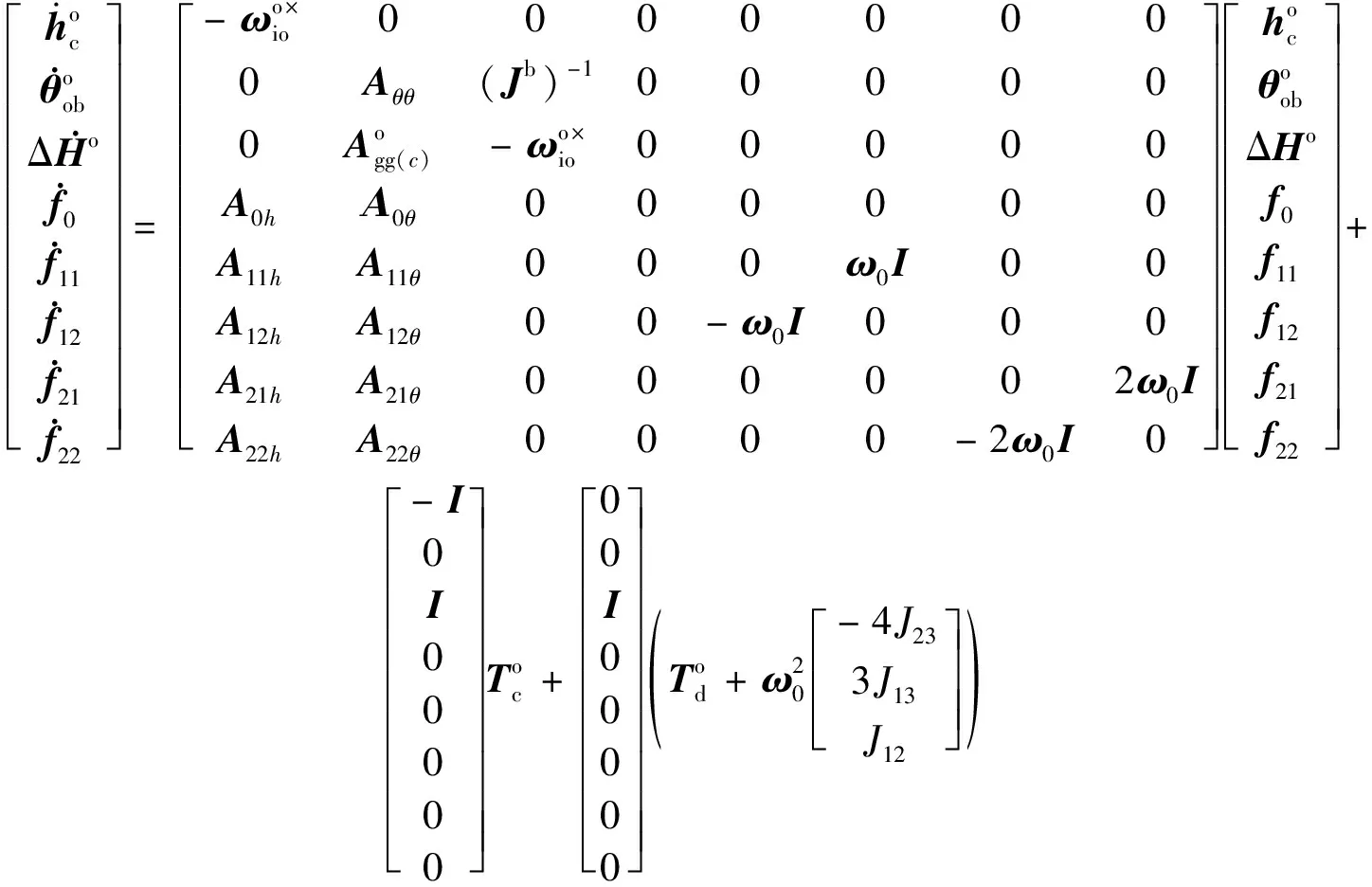
(17)

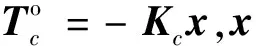
2 控制器设计

2.1 基础引理

定义1[10].对于复平面中的区域D，如果存在一个对称矩阵L∈Rm×m和矩阵M∈Rm×m，使得

(18)

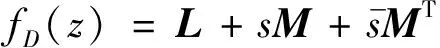
定理1[10]在给定2个LMI区域D1和D2的情况下，矩阵A同时是D1-稳定和D2-稳定的充要条件是存在对称正定矩阵X，使得

(19)

考虑如下不确定系统：

(20)

式中:x(t)为系统的状态变量；u(t)为系统的控制输入；v(t)为干扰项，Δ是一个反映模型参数不确定性的未知矩阵，并假设其满足ΔTΔ≤I。A、H、E、B为相应维数的常矩阵。

定理2 对于式(20)定义的系统，采用状态反馈u(t)=Kx(t)，将极点配置在由条形区域和扇形区域共同构成的梯形区域内(如图1)且保证一定鲁棒稳定性的充要条件是：存在标量ε>0和一个对称正定矩阵X、矩阵W同时满足

(21a)

(21b)

反馈增益矩阵为K=W/X。

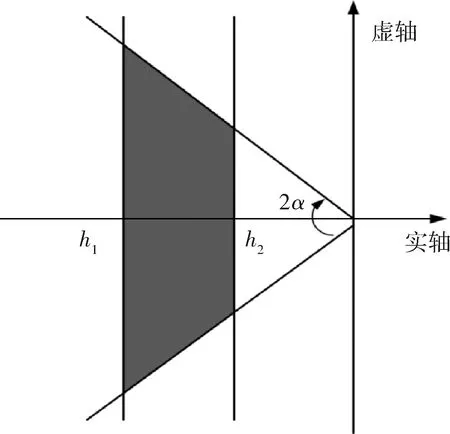
图1 极点配置的梯形区域

证明：由定理1及参考文献[10]可知，矩阵A的特征值位于区域D1(条形)和D2(扇形)组合而成的梯形区域内的充要条件是存在对称正定矩阵X，同时满足

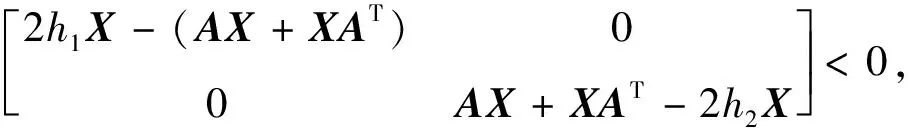
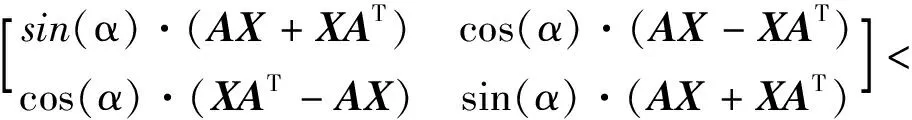
对系统(20)引入状态反馈u(t)=BKx(t)，同时使其在区域D1内具有一定的鲁棒稳定性，上面两式可变为

(Ⅰ)

(Ⅱ)

其中，A1=A+BK+HΔE；A2=A+BK，对式(Ⅰ)分解可重新写成

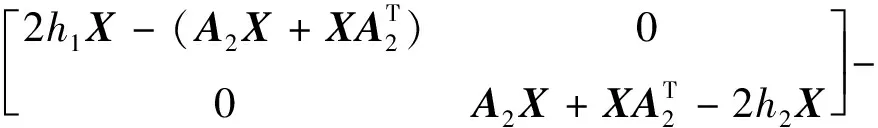
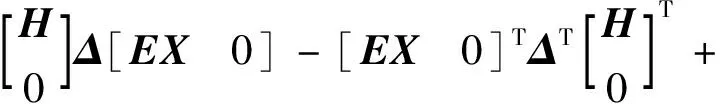
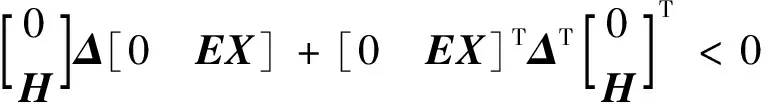
由文献[10]可知，上式对满足ΔTΔ≤I的所有不确定矩阵Δ成立当且仅当存在标量ε>0，使得

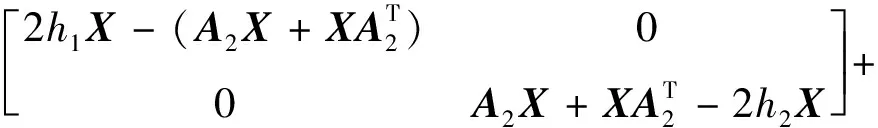
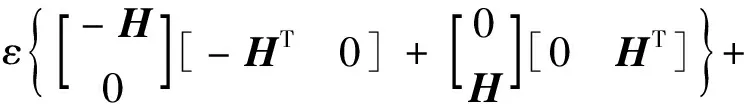
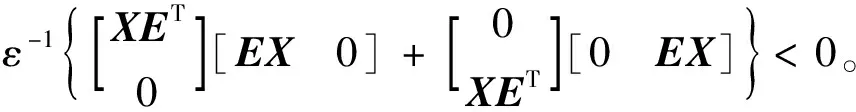
整理上式并联立式(Ⅱ)可得

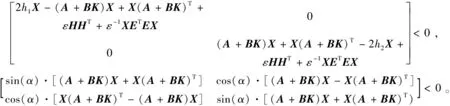
记W=KX，并应用矩阵Schur补性质可得与上面两式等价的式(21)。定理得证。

定理3[4,11]定义变量h∈R，矩阵A∈Rn×n的特征值为λi(i=1,…,n)，令A0=A-hIn×n，In×n为n×n单位阵，下面给出2个矩阵符号函数的定义：

sign+(A0)=1/2[In×n+sign(A0)]

(22a)

sign-(A0)=1/2[In×n-sign(A0)]

(22b)

定义矩阵

(23)

式中：S1=ind[sign+(A0)]∈Rn×n1；S2=ind[sign-(A0)]∈Rn×n2，ind(·)表示(·)的线性无关列向量集合，n1+n2=n。

2.2 基于LMI的控制器设计

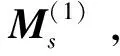
(24a)

矩阵B转化成

(24b)

(25)

(26)

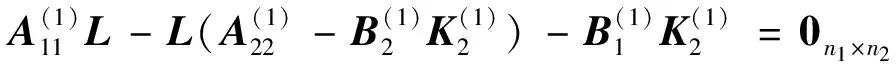
(27a)

(27b)

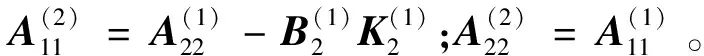
(28)

综上两步设计，累计状态反馈增益矩阵为：

Kc=-[K(1)+K(2)(T(2))-1](T(1))-1

(29)

此时闭环系统矩阵(A-BKc)的特征值位于图1所示的阴影区域内。

3 数学仿真

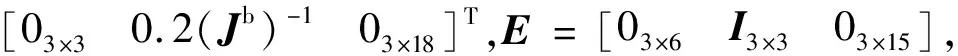
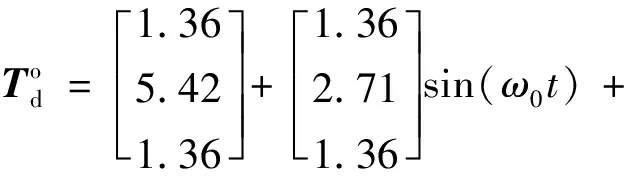
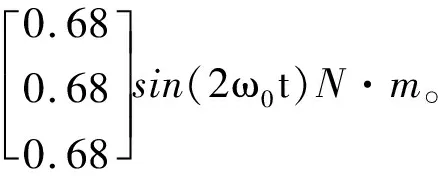
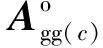
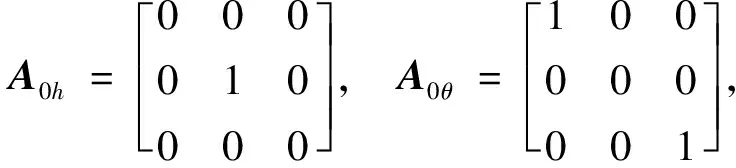
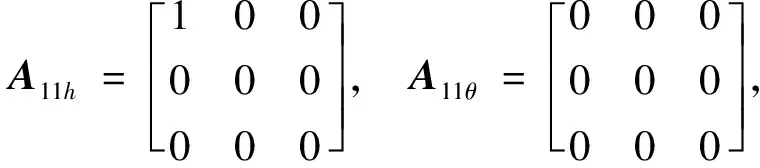
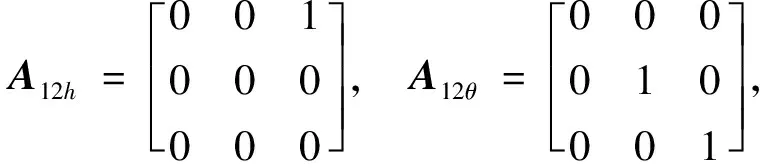
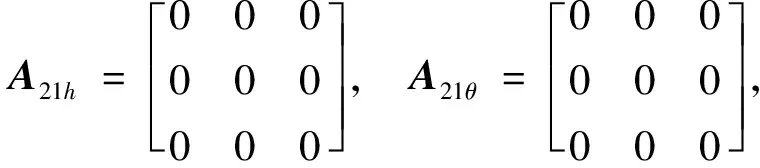
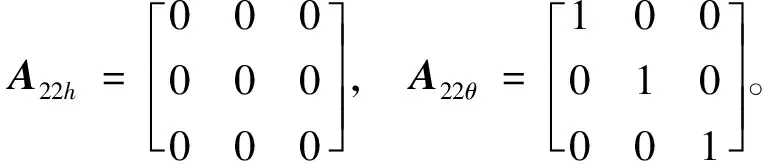
仿真时稳定裕度-h2取0.25ω0，阻尼角α取45°，-h1取值为3.6ω0。设置实数h=-0.5ω0，将原系统分为了3维(h左侧)和21维的子系统，通过控制器多级设计最终极点配置结果如表1、图2和3。

表1 闭环极点(/ω0)

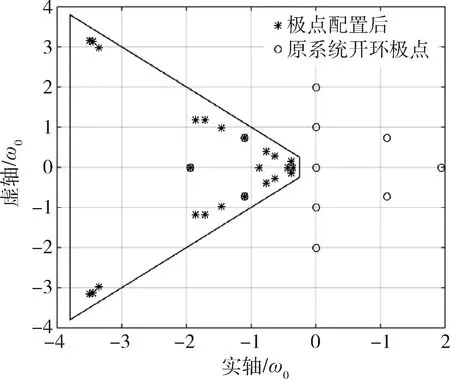
图2(a) 第1步设计后闭环系统极点和原系统开环极点对比

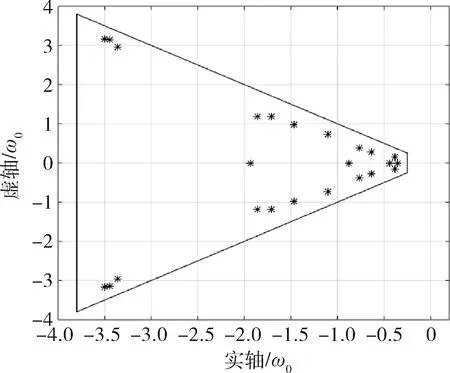
图2(b) 第1步设计后闭环系统极点分布

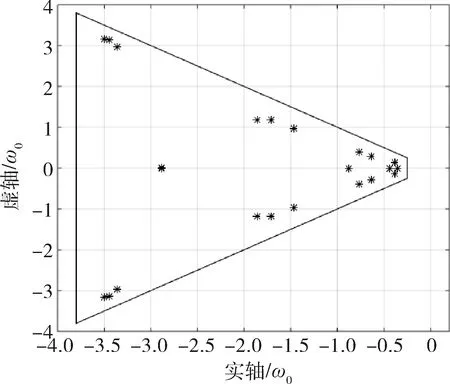
图3 第2步设计后闭环系统极点分布

从图3中可看到所有极点均被配置到了复平面虚轴左边0.25ω0～3.6ω0，且上下张角±45°的梯形区域内。图4～6分别为姿态角、姿态角速率和CMG角动量时域响应曲线，基本在2个轨道周期附近达到稳定状态。从图4可以看到，仿真结果与前面理论计算分析的结果相符，稳态时x0轴姿态具有均值为0°、幅值为0.36°的正弦振动；y0轴姿态偏置接近-8.861°(与前面理论结果一致)，以消除重力梯度力矩和干扰力矩常值造成的角动量累积；z0轴姿态角趋于0°。图5显示空间站三轴姿态角速率也处于较小的量级以内。从图6中还可以看出CMG角动量呈周期性波动，可以消除一部分周期性干扰对姿态的影响，但并没有角动量的积累，所以本文设计的带极点配置的控制器可以达到角动量管理的目的，并得到了预期的结果。

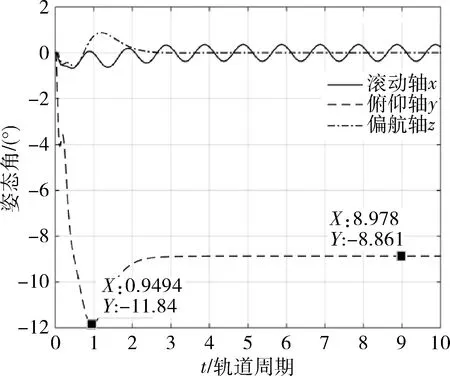
图4 姿态角

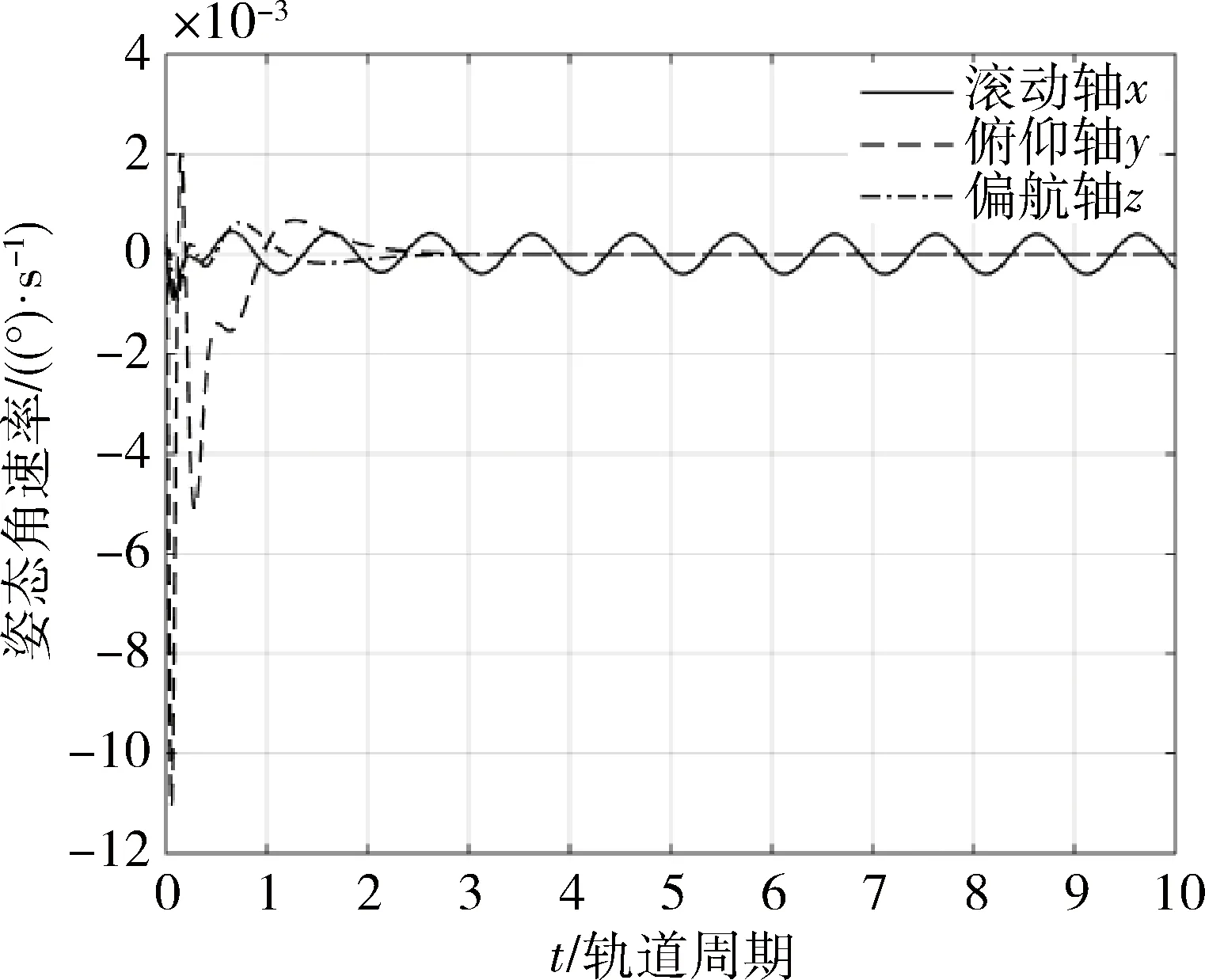
图5 姿态角速率

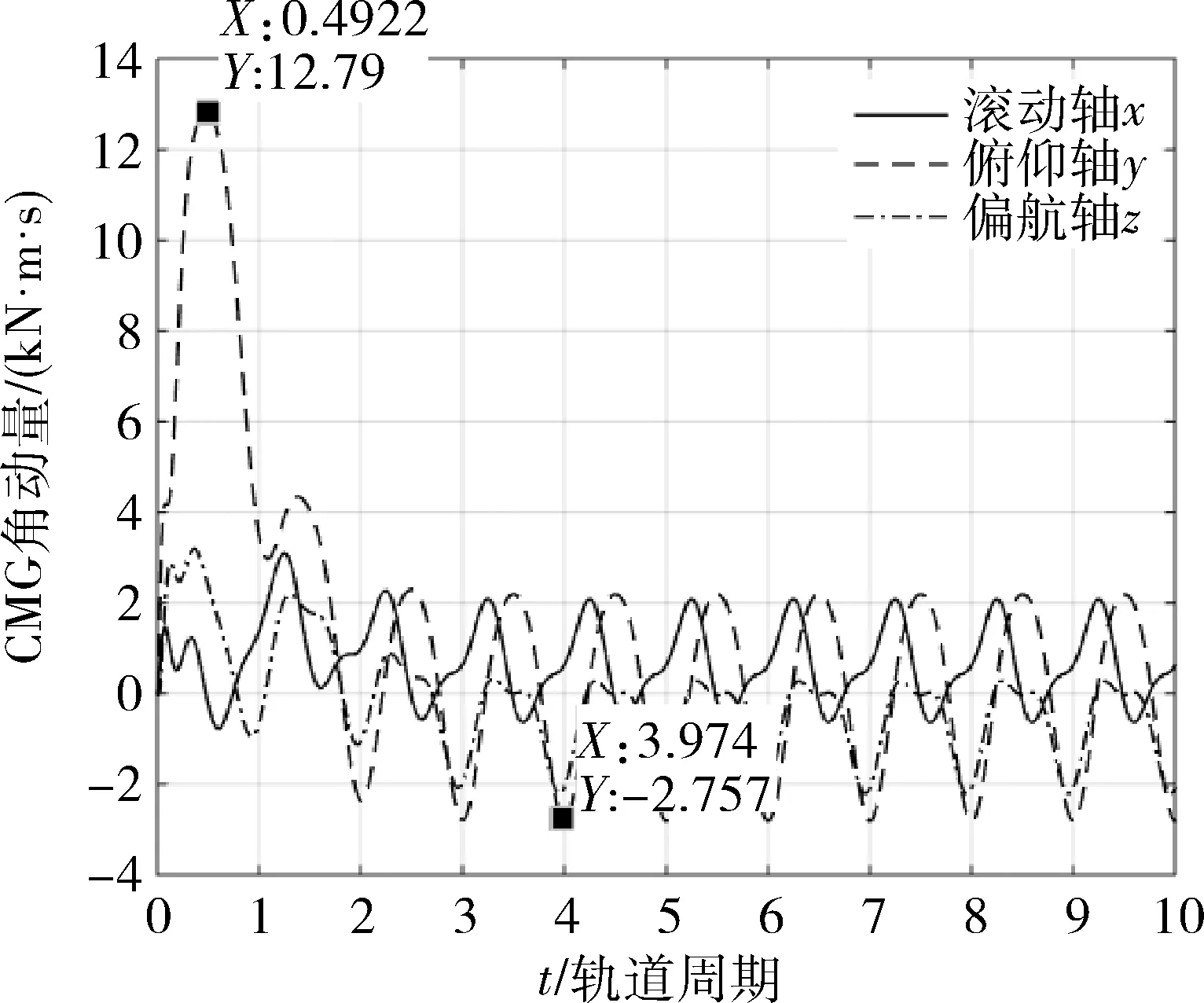
图6 CMG角动量

从表2对比可看出，2种算法下稳定时间、俯仰角超调量以及稳态时偏航与俯仰角变化范围基本一致；相比文献[8]中最新方法，本文算法下角动量超调增加约5%，但是稳态时角动量幅值减小约19%。而且相较LQR算法，本文基于LMI算法的区域极点配置还考虑了不确定系统的鲁棒稳定性；同时通过求解LMI问题实现了梯形区域极点配置，避免了带极点配置的LQR算法中求解Riccati方程时容易遇到的数值奇异问题，以及弥补了LQR算法中扇形区域右边界上限难以事先指定的不足，所以本文方法在取得较好的控制效果的同时更具一般性。

表2 不同算法性能比较

4 结论

针对大型航天器姿态与角动量管理控制问题，基于线性矩阵不等式方法进行了其姿态角动量管理控制器的多级设计。基于矩阵符号函数将高维被控系统解耦为维数较低的子系统，避免了一次性进行反馈增益阵求取时可能遇到的数值奇异问题，采用凸线性矩阵不等式进行系统多目标约束描述，实现了系统极点在指定梯形区域的极点配置，弥补了传统LQR方法加权矩阵的选取和迭代试凑的问题，以及带极点配置的LQR算法因分步设计而无法进行指定封闭区域极点配置的不足，实现了系统动态、稳态性能以及鲁棒稳定设计，仿真验证了控制器的有效性。