永磁直线电机结构参数的DFSS和响应面法优化
张 啸,肖文生,王全宾,王舒慧
(1.中国石油大学(华东)机电工程学院,山东 青岛 266580;2.中国石油勘探开发研究院,北京 100083)
1 引言
圆筒型永磁同步直线电机是往复电潜柱塞泵采油系统的动力机,具有推力大、传动刚度高、行程不受限等优点,它能将电能直接转换为往复直线运动,减少了机械转换环节,提高了传动效率。同时可以实现大功率、大位移的无摩擦驱动,近年来已成为原油开采领域的热点[1]。六西格玛设计(DFSS)[2]是一种以质量经济性为原则,以顾客为中心的高效设计理念和方法。结合数理统计理论对相关设计参数与系统性能之间关系进行量化,在保证可靠性、低成本、短周期的基础上,实现六西格玛质量水平,在产品优化设计方面具有很高实用价值。在直线电机设计过程中,参数组合对电机性能影响显著,各个参数的优化匹配,能大幅提高电机运行性能。文献[3]针对低速大扭矩潜油同步电机研究了影响电机效率与齿槽转矩的电磁结构参数;文献[4]根据麦克斯韦张量定理研究了圆筒永磁直线电机的结构参数与单边磁拉力的关系;文献[5]等基于响应面法以平板型直线电机重量因素为优化目标进行了参数优化研究,实验结果证明响应面法在电机参数匹配研究中的可行性;文献[6]对类哈尔巴赫排列下不同永磁体本体结构参数进行研究,对比分析了其对磁场分布和电磁推力的影响;文献[7]采用支持向量机回归建模方法建立直线电机数学模型,并结合遗传算法对5个本体结构参数进行了多目标优化;文献[8]针对圆筒型直线电机提出了满足工况要求的减小损耗增大效率的定动子外径比、永磁体排列角度、极距3个参数的优化设计方法,对各参数与电磁性能关系进行了量化分析。但是对实际较为复杂的电机结构多参数优化问题,上述分析的因子变量较少,综合多因素变量对电机性能的影响仍然缺少准确高效的优化方法。
针对一种新型的圆筒型永磁同步直线电机为研究对象,开展电机优化方法研究。基于DFSS部分析因实验设计,对直线电机本体结构参数进行量化分析,寻找关键因素,结合响应面优化方法建立显著因子二阶响应模型,并利用多目标算法寻优获取最优参数组合,为潜油直线电机参数优化设计提供了一套行之有效的方法。以114系列半闭口槽10极9槽低速圆筒型潜油永磁同步直线电机单体电机为载体进行电磁参数的优化设计研究,电机参数,如表1所示。

表1 单体电机额定数据Tab.1 Single Motor Rated Data
2 基于DFSS部分析因实验设计
2.1 电机模型及本体结构参数
电机结构模型,如图1(a)所示。电机为隐极式交流电动机,主要由定子铁芯、集中绕组、永磁体、导磁体、隔磁环等几部分组成。电机初级为模块化硅钢结构,次级采用梯形和矩形永磁体复合阵列,实际工作过程中由单体电机多级串联以实现电机额定行程。影响圆筒型永磁直线电机性能指标的结构参数较多,定义了模型主要电磁结构参数及永磁体充磁方式,如图1(b)所示。
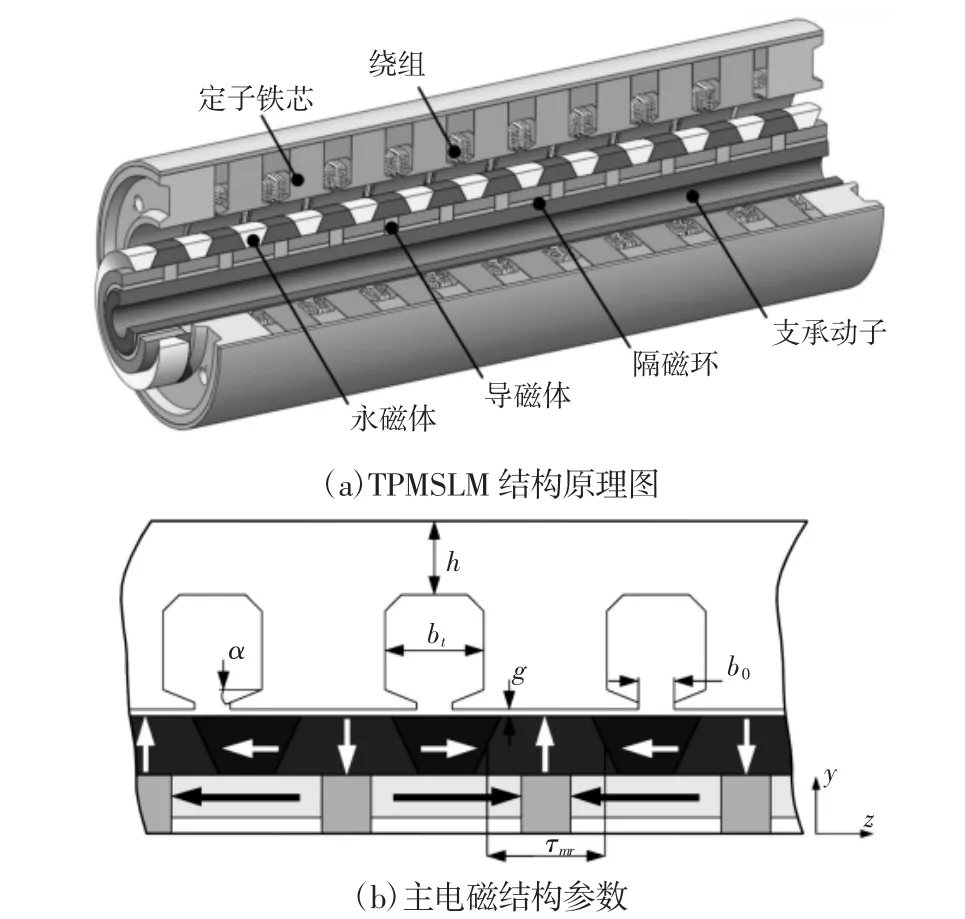
图1 圆筒型永磁同步直线电机结构图Fig.1 Schematic Structure of the TPMSLMs
图中:g—气隙长度;h—轭厚;bt—齿宽;α—齿形角;τmr—主磁通永磁体有效长度;b0—半闭口槽宽度。
在初始值上、下各取一个值作为优化设计的高水平和低水平值,确定优化区间,如表2所示。区间范围由以下约束确定:(1)电机齿磁密Bt≤1.5T,定子轭平均磁密Bj≤1.3T;(2)槽满率Sf≤80%;(3)绕组电流密度 J≤5A/mm2;(4)动子轴的直径 D≥20mm;(5)定子齿型为倒T型结构。
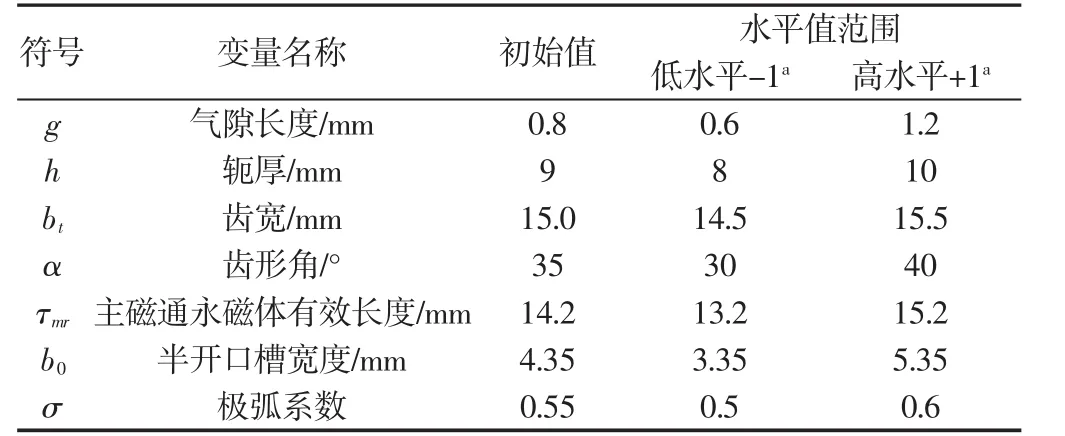
表2 结构参数初始值及取值范围Tab.2 Structural Parameters Initial Value and Range of Values
2.2 部分析因实验设计
部分析因设计[9]是一种多因子实验设计统计方法,能大幅减小实验次数,量化各因子及其交互作用对考察指标的效应,在一定范围内快速准确地得到最佳实验条件。针对表2中7个主体结构参数进行实验设计的因子分析,分析各参数及交互高次项对电机推力及齿槽力的影响。采用2IV7-2部分析因实验设计法,共7个因子2项水平,另外加入1个中心点,测模型弯曲度,共17组实验。实验响应值的数据收集可通过电机实测或仿真获得,但实测需加工17组不同规格的工程样机,成本极其昂贵。采用Ansoft软件对电机进行电磁仿真,获得不同参数匹配下的电磁推力及齿槽力并填入设计表中作为实验响应值,如表3所示。表中:FT—电磁推力均值;FD—齿槽力均值。
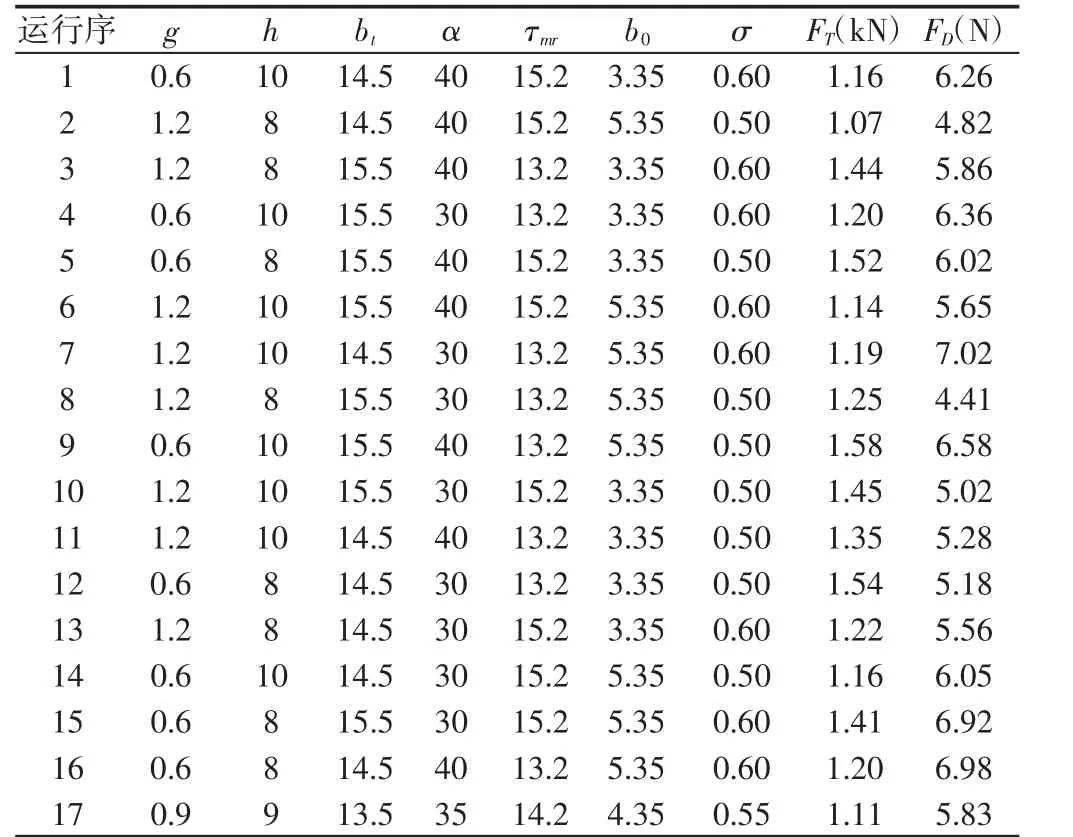
表3 2IV7-2实验设计及结果Tab.3 2IV7-2 Fractional Factorial Design and Results
2.3 显著因子筛选
正态概率图是用于检验实验数据是否符合正态分布的一个技术图表。如果数据符合正态分布,则其上的点应该近似形成一条直线,否则数据点远离直线[10]。Pareto图常用于判断各项效应的显著程度,将各效应的t检验所获得的t绝对值作为横坐标,设定显著性水平αs以获取t值的临界值,t绝对值大于临界值的因子项被视作显著效应项。显著因子的响应值在高低水平差异很大,而非显著因子的差值就很小。因此,通常采用Pareto图来反应各因子及其交互作用在不同水平的差异大小。该部分析因实验设计利用Minitab软件得到的响应为推力时的标准化效应图,如图2所示。
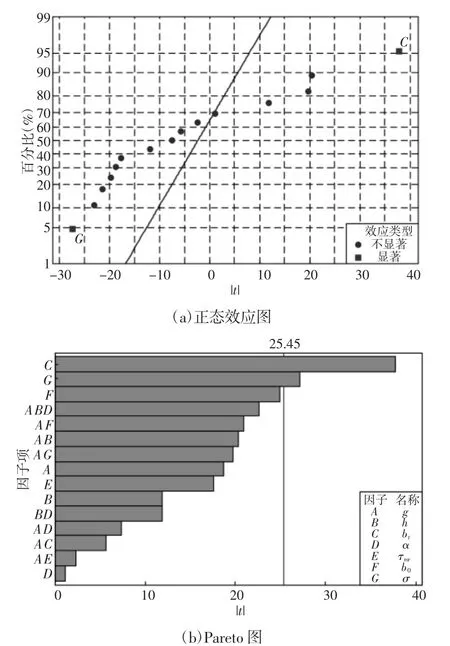
图2 标准化效应图(响应为推力)Fig.2 Standardized Effects for Thrust
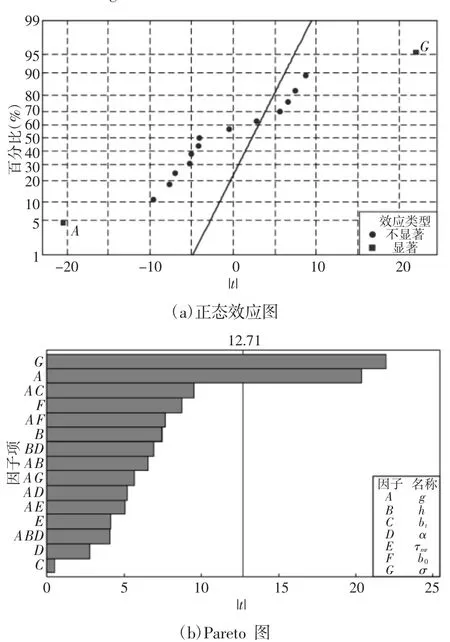
图3 标准化效应图(响应为齿槽力)Fig.3 Standardized Effects for Cogging Force
响应为齿槽力时的标准化效应图,如图3所示。当显著性水平αs=0.05时,点G(极弧系数)、A(气隙长度)的影响值远离直线,表明其为对响应有显著影响的因子。其中,A对齿槽力的影响是为正效应,而G对齿槽力的影响是为负效应。同样没有显示交互效应项为显著因子,因此也无需分析混杂情况,即:极弧系数、气隙长度为影响齿槽力的显著因子。
3 响应面模型分析及优化
对于复杂电磁力的计算问题,功能函数往往是高阶非线性和隐式的。响应面法(RMS-Response Surface Methodology)是基于数理统计理论,针对多变量问题进行建模和分析的一种统计处理技术。其利用显式响应面函数拟合真实复杂的功能函数,将复杂隐式功能函数的电磁力转换为简单显式的功能函数,为了得到更加精确的弯曲响应,通常采用含有交叉项的二次多项式表示的响应面函数[11]:
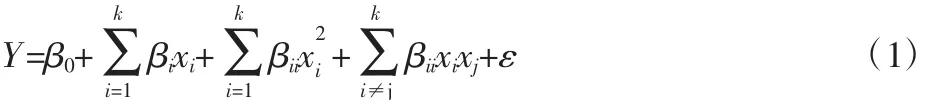
在确认了三种显著因子后,利用响应曲面模型分别建立响应方程,获取产生最佳响应的因子设置。选取中心复合表面设计(CCF)建立推力和齿槽力的响应面模型。齿宽x1、极弧系数x2和气隙长度x3为电磁推力及齿槽力的响应面模型优化设计变量。根据新的设计变量在CCF决策空间中构造出13个试验点,并通过Ansoft有限元分析获得响应值,分别建立两种响应面模型为:ˆ
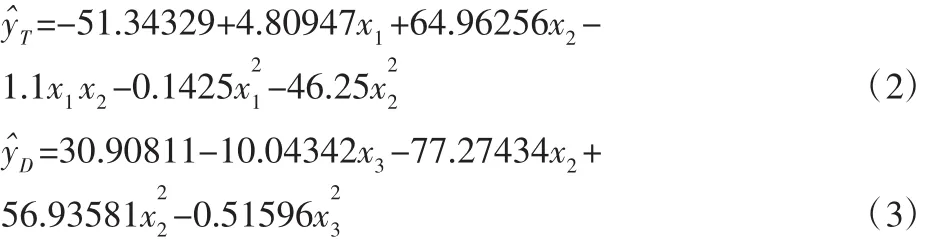
两种响应面模型的回归模型方差分析表,如表4、表5所示。
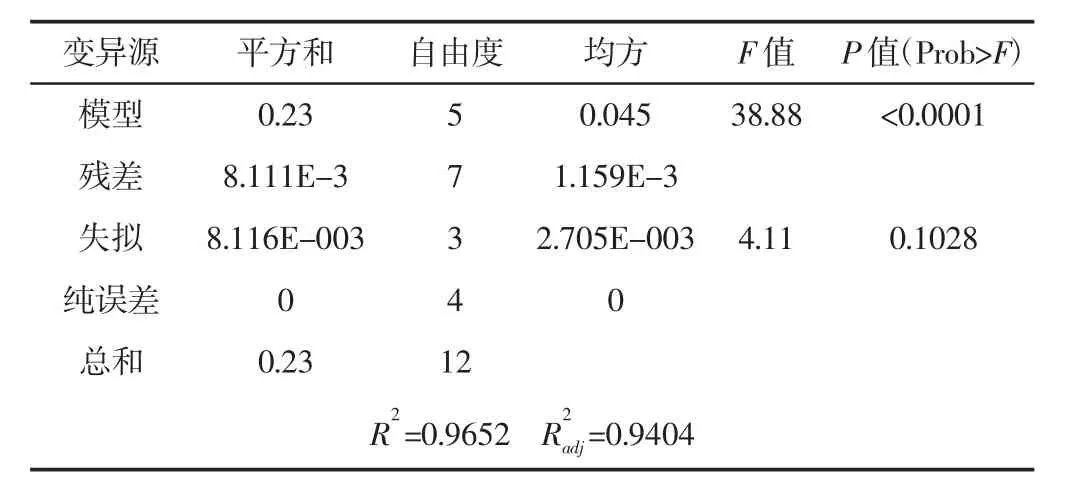
表4 推力回归模型方差分析表Tab.4 Analysis of Variance of Thrust Regression Model
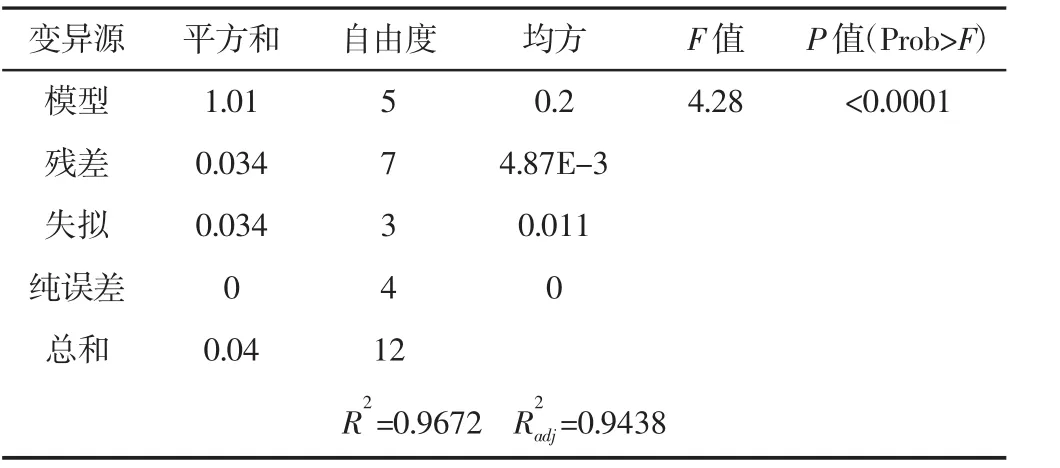
表5 齿槽力回归模型方差分析表Tab.5 Analysis of Variance of Cogging Force Regression Model
由表4可以看出,推力拟合回归方程达到高度显著(模型p<0.0001),判定系数 R2=0.9652,修正判定系数 Radj=0.9404,两者大小接近且接近于1,表明拟合的推力二阶模型有效精确。由表5可知,齿槽力拟合回归方程同样达到高度显著,修正判定系数=0.9438,判断系数R2=0.9672,表明近94%的实验数据变异性可用此模型解释。由此可见,两种回归模型与实际的拟合度较好,能准确预测齿槽力和电磁推力。
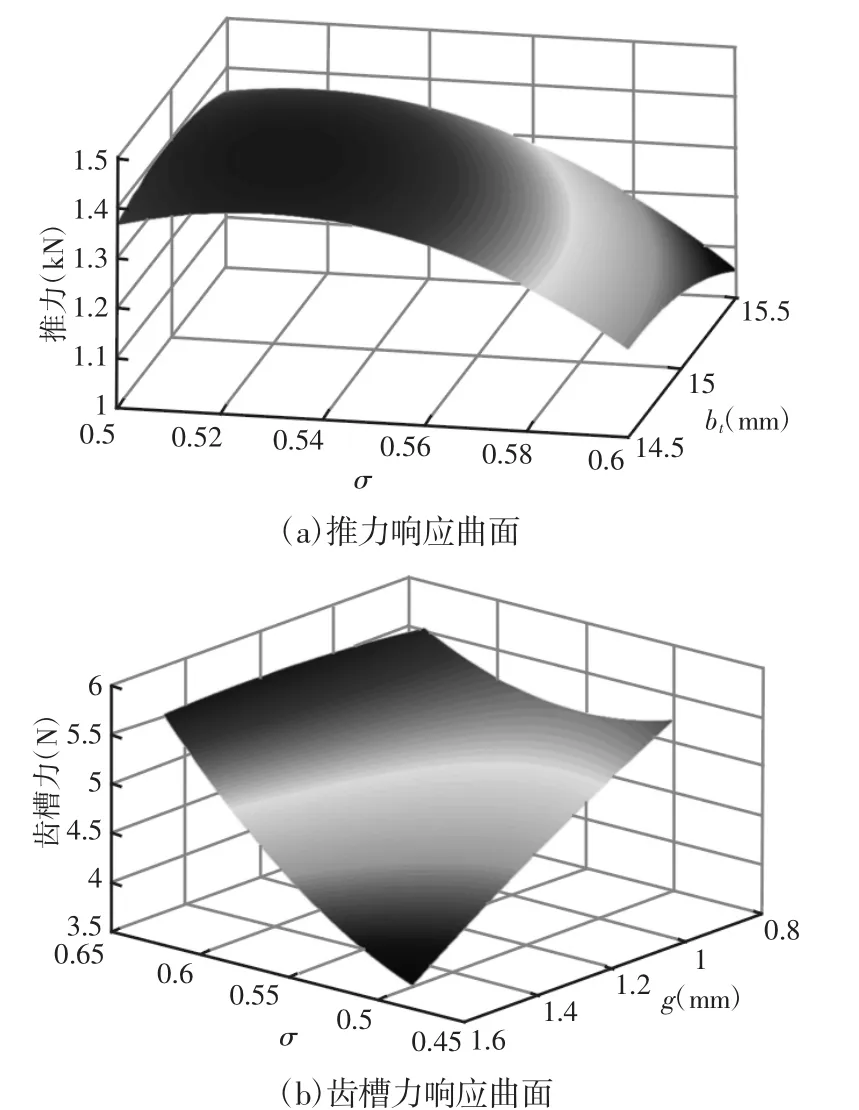
图4 响应曲面图Fig.4 Response Surface Map
响应曲面,如图4所示。齿宽与极弧系数对电磁推力的综合效应,如图4(a)所示。气隙长度与极弧系数对齿槽力的综合效应,如图4(b)所示。但是,无法同时获取最大电磁推力及最小齿槽力的各项因子值,需通过多目标优化算法寻找最优解。
4 多目标算法寻优
电磁结构参数优化的目的是选出一组满足电磁推力较大、齿槽力较小时σ、bt和g的结构参数组合,这是一个多目标优化问题;基于遗传算法的多目标算法可以直接作用该拟合模型进行寻优。Gamultiobj函数是基于NSGA-II算法改进的一种多目标优化算法,能较好解决多目标优化问题[12]。因此,采用Gamultiobj函数对响应面模型进行多目标优化。建立函数fmin(x)时,需要对优化目标函数进行变换,将推力函数取负数,进行最小值求解。该多目标优化数学模型可以表示为:

式中:f1(x)和f2(x)—电机推力函数和齿槽力函数;
xil和xih—第i个变量取值的下限和上限;
x1~x3—σ,bt,g。
多目标优化问题各个设计变量之间以及各个目标之间可能存在相互作用,不可能找到一组设计变量让所有目标同时达到最优,只能对其进行折中处理,获得Pareto最优解集。根据表2所示的设计变量的取值范围,通过多目标算法优化后获得Pareto前沿,如图5所示。

图5 优化后Pareto前沿Fig.5 Schematic Diagram of Pareto Frontier
取A点作为折中解,在A点对应的最终优化结果及最优参数组合,如表6所示。根据优化后的参数匹配结果进行有限元仿真分析,优化前后结果对比情况,如表7所示。优化结果与拟合值存在差异,原因如下:
(1)拟合值是通过求解近似函数获得,与真实函数存在差异;
(2)拟合模型中只考虑了3个变量,而在最优参数匹配有限元分析中考虑了电机所有电磁参数,并且各参数之间存在交互效应。优化后,电机推力及齿槽力都有很大的改善:平均电磁推力提升了28.83%,齿槽力降低了18%。优化前后永磁直线电机的电磁推力及齿槽力曲线图,如图6所示。推力波动和齿槽力波动均大幅度减小,电机性能显著提高。

表6 最优参数组合Tab.6 Optimal Combination of Parameters

表7 优化前后性能指标对比Tab.7 Comparison of Performance Before and After Optimization
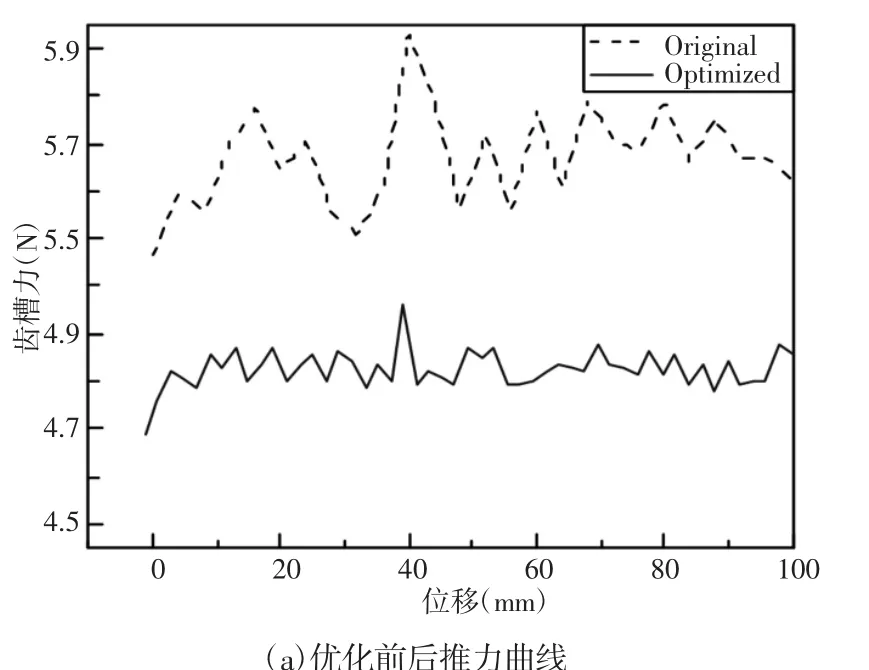
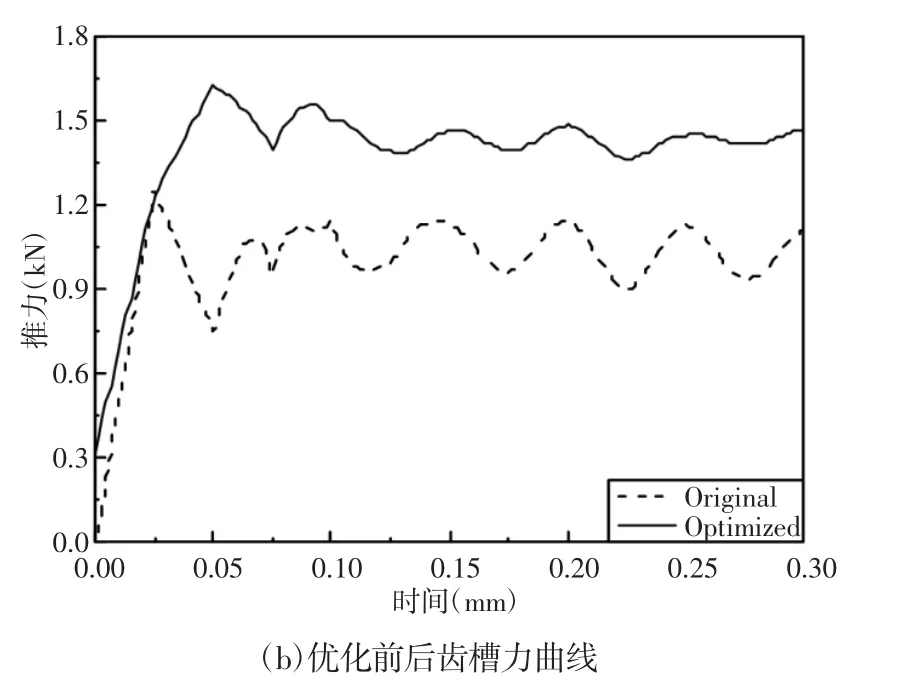
图6 优化前后电机推力和齿槽力曲线图Fig.6 Comparison of Thrust and Detent Force
5 结论
以潜油圆筒型永磁同步直线电机电磁结构参数为优化变量,电磁推力及齿槽力为优化目标,提出了一种基于DFSS设计理念和响应面法的优化设计方法。利用Ansoft进行电磁仿真,采用7因素2水平的部分析因实验设计对电机主体结构参数进行优化。分别筛选出了影响电磁推力和齿槽力的显著因子。筛选结果表明极弧系数及槽深是响应为推力时的显著因子,极弧系数与气隙长度是响应为齿槽力时的显著因子。结合响应面优化方法建立显著因子与电机性能指标的二阶响应面模型,为电机的多目标优化提供了精确的理论模型。采用多目标优化算法寻优,获得最优参数组合。优化结果表明,平均电磁推力提升了28.83%,齿槽力降低了18%,推力波动和齿槽力波动均大幅度减小,电机性能显著提高,说明了优化方法的有效性和可行性。

