真空管道磁悬浮列车混合EMS支承的设计与分析

胡业发，张 宇，施梦瑶，吴 帆

（武汉理工大学机电工程学院，湖北 武汉 430070）

1 引言

真空管道磁悬浮列车[1-3]将磁悬浮列车置于近似真空的管道环境中运行，具有无机械摩擦、低噪音、低阻力、低能耗、高运行速度等特点；是一种具有广阔发展远景的交通工具。然而密封的真空管道、超远的运输距离以及更高的运行速度等极限条件对磁悬浮列车的悬浮支承结构提出了新的要求。当前投入商业运行的磁悬浮列车基本都是EMS（Electromagnetic Suspension）型，这种纯励磁结构需通入大量电流来产生系统所需要的悬浮力，其中线圈会产生电阻损耗，产热较多、功耗较大[4]。文献[5]将超导线圈引入悬浮系统中，利用超导线圈提供系统平衡悬浮力，常导线圈提供系统悬浮的调节电磁力，这种混合电磁铁虽然能提高磁场强度降低能耗及耗热，但它需要一套专门的冷却系统、结构复杂而且造价昂贵；近来，随着价格低廉且性能优良的稀土永磁材料的兴起，一种由永久磁铁产生静态偏置磁场提供主要悬浮力，而电磁线圈只提供悬浮控制力的混合支承系统受到国内外学者的广泛关注和研究；一些学者如文献[6-7]在中低速列车的电磁铁中加入永磁体，并给出了一些基本结构方案和U型磁铁的参数设计准则，但其电磁性能分析还有待深入研究。

将混合EMS支承应用于真空管道磁悬浮列车之中，以实际需求出发，建立了适用于圆形管道的弧形混合支承模型，利用等效磁路法确定混合支承结构参数，通过ANSYS Maxwell对列车满载稳定悬浮、满载起浮、空载锁死三种临界工况下混合EMS支承的磁场分布以及电磁力随电流变化情况进行仿真模拟，对比验证了结构设计的合理性，能有效降低系统能耗，为混合EMS支承结构在真空管道运输系统中的应用提供了参考。

2 混合EMS支承的结构

真空管道磁悬浮列车系统整体结构示意图，如图1所示。圆弧形轨道衔铁（2）和6个W弧形混合电磁铁（3）与竖直方向呈37°分别对称布置于真空管道（1）和胶囊列车（4）斜上方，形成吊轨上吸式悬浮，牵引直线电机（5）动子安装于列车下方，定子安装在管道底部，两侧设有安全支撑轮（6）。磁悬浮胶囊列车车身结构参数参考美国太空探索技术公司公司设计的文献[8]进行设计，车身内径约2.5m，车长约10m，额定载客12人，满载重量约7t，空载总重量约6t，设计时速1000km/h。

图1 真空管道磁悬浮列车系统示意图Fig.1 Schematic Diagram of the Vacuum Tube Magnetic Levitation Train System

列车上电磁铁对称布置，可以实现机械解耦，故以单个混合电磁铁为分析对象。其结构原理，如图2所示。当列车处于平衡位置时永磁铁磁通产生的电磁力保持车体的稳定悬浮；当受到外界干扰远离轨道时，系统给电磁线圈施加正向电流产生与永磁体磁通方向一致的磁通相互叠加，进而产生大于列车重力的电磁力，使列车向平衡位置移动；反之，受到外界干扰偏向轨道时，系统给电磁线圈施加反向电流，从而产生与永磁体磁通方向相反的磁通相互叠加产生小于列车重力的电磁力，在合力的作用下使列车回到平衡位置。

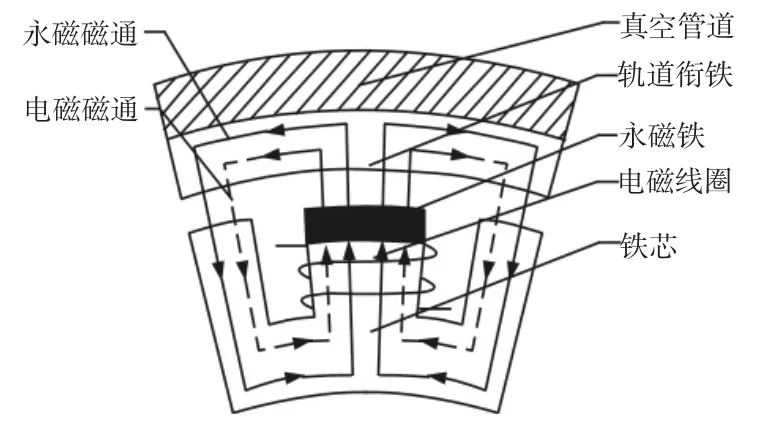
图2 混合电磁支承结构原理图Fig.2 Schematic Diagram of Hybrid Electromagnet Structure

3 混合EMS支承结构参数设计

对真空管道磁悬浮列车混合支承设计，要求在保证提供足够悬浮力和导向力的同时尽可能减小支承系统的体积，进而达到节能减重与降低成本的目标。因此，以电磁铁的悬浮力为边界条件，以系统的节能减重作为目标函数对该混合支承进行设计计算。

3.1 混合EMS支承磁路模型

针对混合电磁支承的结构设计，首先进行如下假设[9]：

（1）铁磁材料的磁导率无穷大且磁势分布均匀；

（2）忽略混合系统的磁漏；

（3）忽略电磁铁的弹性与刚度变形；

根据上述条件，建立该混合支承结构的等效磁路模型，如图3所示。

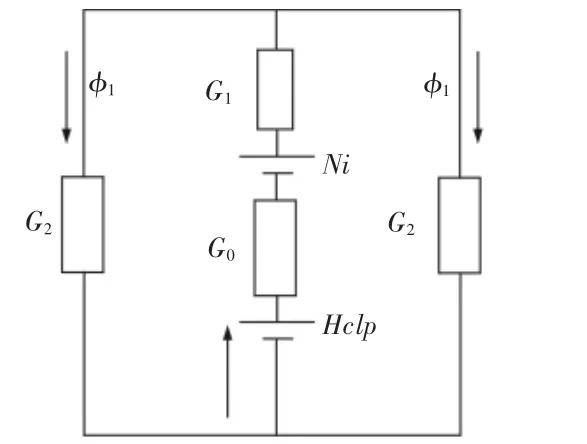
图3 混合EMS支承等效模型Fig.3 Equivalent Magnetic Circuit Diagram of Hybrid EMS

图中：G0—永磁铁的内磁导；G1—永磁极的气隙磁导；G2—两端磁极处气隙磁导，其中：

由磁路的戴维南定理可得系统的总磁导为：

式中：x—轨道和混合电磁铁之间的气隙长度，mm；μ0—真空磁导率，H/A；μr—永磁铁的相对磁导率；Sp—永磁极横截面积，m2；Lp—永磁铁的磁体厚度，m。

根据克希荷夫定律：F=0和Σφ=0，可求出磁路的总磁通：

式中：N—电磁铁线圈匝数；i—线圈中通过的电流，A；Hc—永磁体的矫顽力，A/m。

所以该磁路的磁感应强度为：

根据虚位移法得到电磁力F的公式[9]为：

由于混合电磁EMS支承结构两端磁极的面积是中间磁极的一半，所以：

联立式（1）～式（8）得出混合EMS支承的悬浮力为：

3.2 混合EMS支承中永磁体参数设计

列车满载处于额定悬浮间隙即x=10mm时，由永磁体提供悬浮力，基本实现零功率悬浮，这即为永磁体设计的依据；此时的电流i=0A，其永磁悬浮力为：

当列车稳定悬浮时：FP=ζmg/cos37° （11）

式中：m—真空管道磁悬浮列车满载重量，kg；ζ—安全系数；

联立式（10）～式（11）可得永磁体的长度：

由上式可以看出，LP与SP不是独立的，当磁极面积确定后，永磁体长度也唯一确定。如果期望电磁铁的体积最小，那么永磁铁磁极面积与体积也必然最小，所以以永磁体的最小体积为设计目标函数[10]，即：

对式（14）求导并求取最优解为：

3.3 混合EMS支承中电磁线圈参数设计

混合电磁铁在额定间隙时所需安匝数为零，而在偏移平衡位置时并不为零；当系统围绕额定间隙上下波动时，只需要改变平衡安匝数电流大小与方向。根据分析可知，混合电磁EMS支承的最大安匝数必然发生在偏离平衡位置最远处。根据式（9）可得：

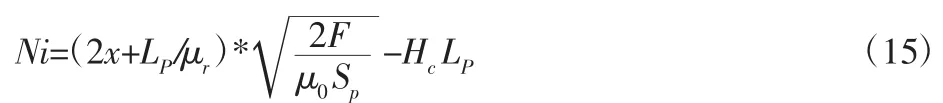
分别将X=Xmin=5mm与X=Xmax=15mm带入上式，取安匝数大者为设计标准。根据设计最大电流Imax，可以求得线圈匝数N。

3.4 混合EMS支承中磁极长度与宽度设计

当混合电磁EMS支承磁极面积确定后，需选取适当的长度与宽度。而电磁铁的磁极的长宽比越大时涡流效应越小，其悬浮力就越大，但过大的长宽比会导致电磁铁刚度较低，使得安装固定和加工十分困难，一般采取多个电磁支承多点分布的形式，每个电磁铁长度不宜超过1米[10]。

综上所述混合EMS支承结构的主要设计参数，如表1所示。

表1 混合EMS支承的主要设计参数Tab.1 Main Design Parameters of Hybrid Electromagnet

4 临界工况下电磁力仿真分析

真空管道磁悬浮列车设计满载总重量约7t，空载总重量约6t，总共装载6套混合EMS支承装置，由式（11）可得每个电磁铁重载荷承重14583N，空载承重12500N。混合EMS支承是按照以下三种临界工况设计：

（1）列车处于满载10mm平衡悬浮间隙，此时由永磁体提供悬浮力，基本实现零功率悬浮；

（2）列车处于满载15mm起浮临界间隙，此时由永磁体和电磁线圈共同提供系统的悬浮力，从而将列车拉回平衡位置；

（3）列车处于空载5mm锁死临界间隙，此时电磁线圈通入反向电流产生电磁力抵消永磁力，从而使列车回到平衡位置。

4.1 满载10mm平衡悬浮间隙

10mm间隙下，不通入电流时的磁感应云图，如图4所示。衔铁的磁感应强度在靠近永磁铁两端处最大，这是由于轨道衔铁与永磁体两端相邻处是主磁通和漏磁通都相对集中流过的部位。而在电磁铁芯中，最大磁感应强度发生在线圈槽的拐角处，因为拐角处相对面积较小，磁通相对集中。该混合支承衔铁与铁芯间隙的磁感应强度在（0.5～0.7）T之间，约为硅钢片剩余磁感应强度的一半。

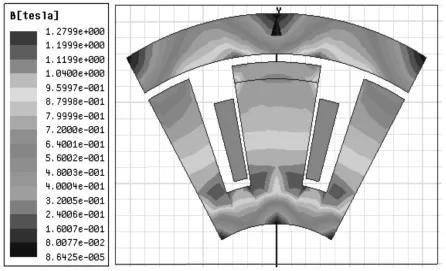
图4 10mm间隙下的磁感应强度分布云图Fig.4 Magnetic Induction Intensity Distribution Cloud Map at 10mm Gap

列车处于10mm平衡间隙时，传统电磁支承与混合EMS支承电磁力随电流变化的情况，如图5所示。从中可以看出，当电流达到19.17A时刚好与列车重量相等；而混合EMS支承结构的电磁力在电流为0A时就达到14306N，接近设计所需的14583N，即在平衡间隙时基本可以实现列车的零功率悬浮；另外，当通入相同电流情况下，混合EMS支承结构的电磁力远远大于传统电磁支承的电磁力，因此当所需电磁力一定时，混合EMS支承结构可以在相同磁极面积下减少悬浮的平衡电流进而减少能耗节约运行成本。

图5 10mm间隙下电磁力随电流的变化Fig.5 The Electromagnetic Force Changes with Current at 10mm Gap

4.2 满载15mm起浮临界间隙

15mm间隙下，如图6所示。当通入电流时，永磁磁通与电磁磁通同向叠加时的磁感应云图，最高磁密仍然在靠近永磁铁两端处和线圈槽拐角；由于永磁场和电磁场相互叠加，使得气隙磁感应强度相对增大，整体最大磁感应达到了1.5T。

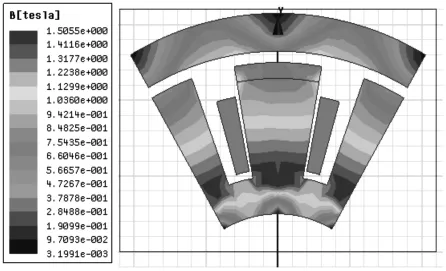
图6 10mm间隙下的磁感应强度分布云图Fig.6 Magnetic Induction Intensity Distribution Cloud Map at 15mm Gap

列车偏离平衡位置到达最大临界间隙15mm，传统电磁支承与混合EMS支承电磁力随电流变化的情况，如图7所示。在0A时，混合EMS支承结构仅产生9320N的悬浮力，不能提供足够的悬浮平衡力，此时电磁部分将通入正向电流提供部分悬浮力，当电流达到10.6A时，才能使列车开始向平衡位置移动；而传统电磁结构需要施加大于28.54A的电流才能使列车向平衡位置移动，混合EMS支承结构相对传统电磁支承所需电流大小减少了62.9%。

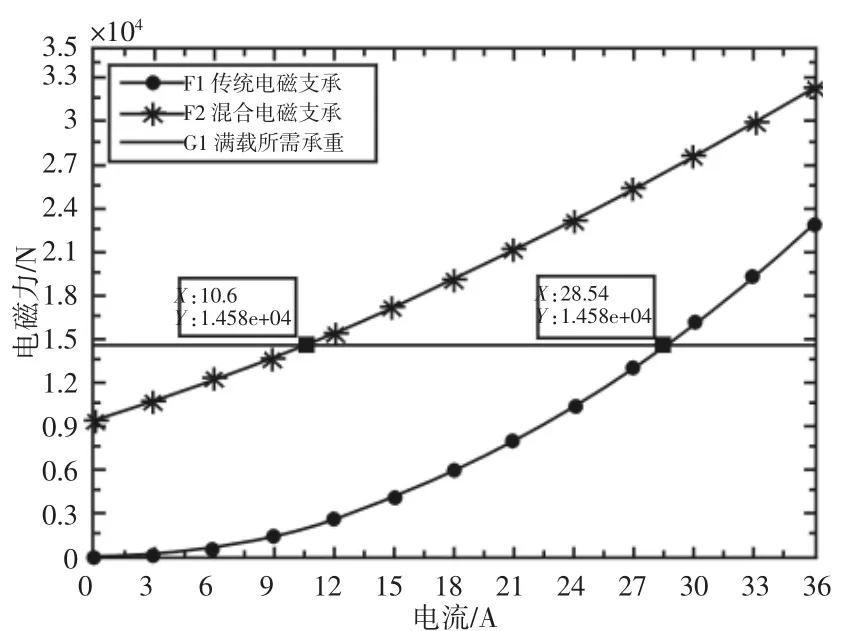
图7 15mm间隙下电磁力随电流的变化Fig.7 The Electromagnetic Force Changes with Current at 15mm Gap

4.3 空载5mm锁死临界间隙

5mm间隙下，通入反向电流时该混合支承的磁感应云图，如图8所示。对比图6，永磁磁通与电磁磁通反向叠加时，中间永磁磁极的磁感应强度明显减小。磁通反向叠加使气隙处的磁感应强度减弱，混合支承产生的磁力小于列车的重力，列车在重力的作用下回到平衡位置。

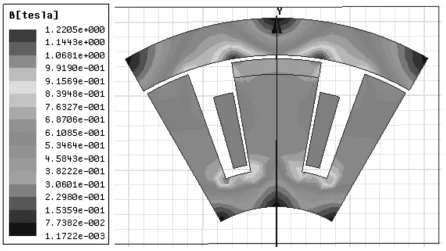
图8 5mm间隙下的磁感应强度分布云图Fig.8 The Electromagnetic Force Changes with Current at 15mm Gap

列车在偏离平衡位置向轨道运动到最小临界间隙5mm，传统电磁支承与混合EMS支承电磁力随电流变化的情况，如图9所示。混合EMS支承结构由于永磁的存在，在电流为0时就将产生高达28000N左右的磁场力，远大于列车的重量，此时需要施加大于13.64A的反向电流来产生反向磁场力来抵消永磁磁场力从而使磁场合力小于车身重力；而传统电磁支承只要较小的电流即可使列车向平衡位置移动，相对而言在小气隙情况下具有一定的调节优势。因此混合支承需要在列车上装载防锁死铜片。

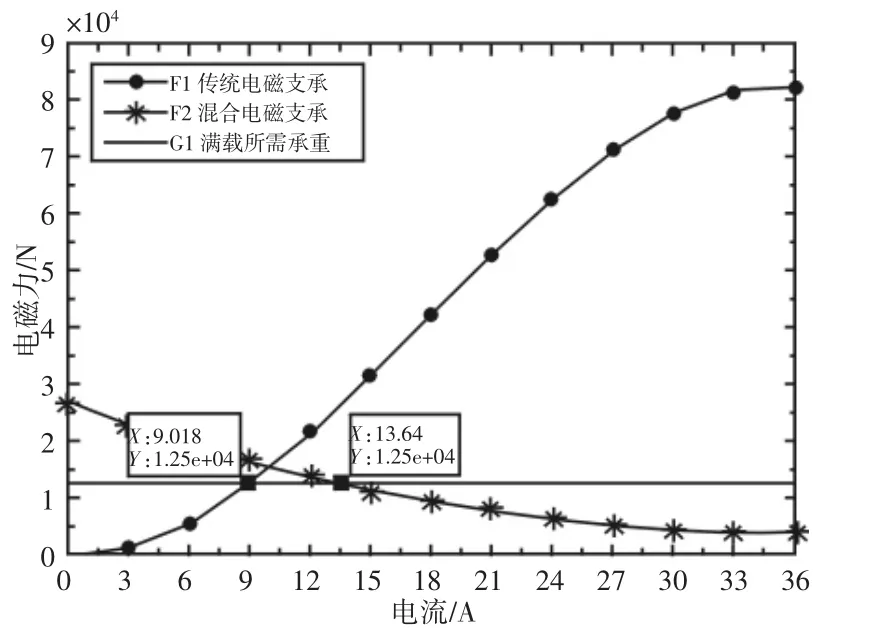
图9 5mm间隙下电磁力随电流的变化Fig.9 The Electromagnetic Force Changes with Current at 5mm Gap

5 结论

将一种弧形混合EMS支承结构应用于真空管道磁悬浮列车之中，利用等效磁路法确定混合支承结构参数，然后建立三维有限元模型，针对满载稳定悬浮、满载起浮、空载锁死三种临界工况对混合EMS支承进行了电磁仿真模拟，得到磁感应分布情况和磁力随电流的变化关系。结果表明：所设计的混合EMS支承结构并能满足悬浮要求。在平衡位置电磁力基本与车重相等，能以较小的电流实现悬浮；在起浮最大临界间隙位置，混合EMS支承结构相对传统电磁支承所需电流大小减少了62.9%。相比传统电磁支承，混合EMS支承具有耗能低、体积小的优点，适用于真空管道磁悬浮列车。