一类定值问题在圆锥曲线中的推广
何重飞
(广州市铁一中学 510600)
文[1]将一些特殊平面图形或空间几何体的定值性质的一系列研究([2]~[4])结论推广到三角形、四边形、正多边形、四面体的“重心圆(或重心球)”,即
命题1[1]以三角形(平面四边形、平面正多边形、四面体)的重心为圆(球)心的任意圆周(球面)上的点到三角形(平面四边形、平面正多边形、四面体)各顶点的距离的平方和为定值.
上述命题的证明笔者采用纯几何法,这并未反映结论成立的实质条件,难于推广. 本文作者从另一个角度,引入参数,建立适当坐标系,将结论进一步推广到圆锥曲线中,得到更一般情形下的定值性质.
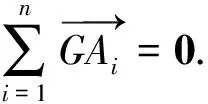
定理1设G为平面(或空间)有限点集Ω={A1,A2,…,An}的重心,则以G为中心的椭圆上的任意一点到A1,A2,…,An距离的平方和与该点到椭圆两焦点距离的乘积的n倍之和为定值.


|PAi|2=(acosθ-xi)2+(bsinθ-yi)2
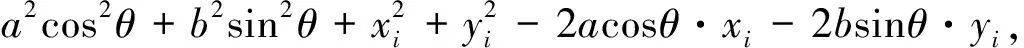
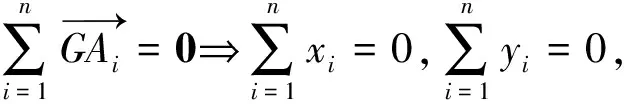
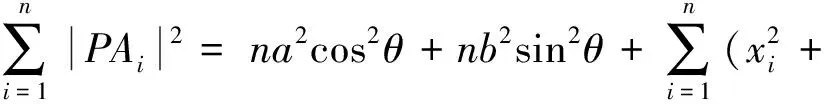
且由椭圆焦半径公式知
|PF1|·|PF2|=(a+ccosθ)(a-ccosθ)
=a2-c2cos2θ=a2-a2cos2θ+b2cos2θ,
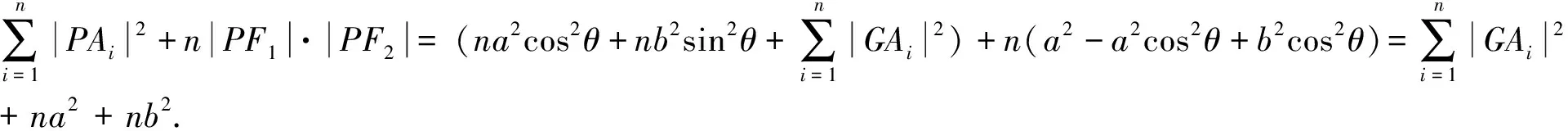

当A1,A2,…,An是空间内给定的n个点时,易知结论依然成立,证明与平面情形类似,在此不再累述.
当椭圆退化成圆,即当a=b=|PF1|=|PF2|=r时,则有
推论1设G为平面(或空间)有限点集Ω={A1,A2,…,An}的重心,则以G为中心,r为半径的圆上的任意一点到A1,A2,…,An距离的平方和为定值.

把圆当成椭圆的退化形式时,
则有a=b=|PF1|=|PF2|=r,


由三角形(平面四边形、正多边形,四面体)重心的性质及推论1即可推得命题1[1].
定理2设G为平面(或空间)有限点集Ω={A1,A2,…,An}的重心,则以G为中心的双曲线上的任意一点到A1,A2,…,An距离的平方和与该点到双曲线两焦点距离的乘积的n倍之差为定值.
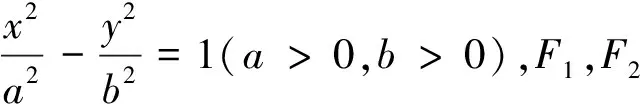

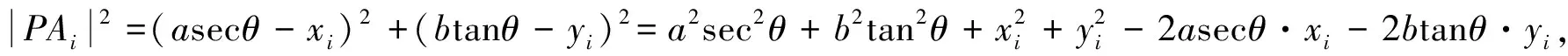
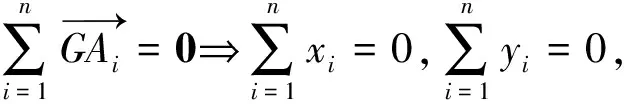

且由双曲线焦半径公式知
|PF1|·|PF2|=|csecθ+a||csecθ-a|
=c2sec2θ-a2=a2sec2θ+b2sec2θ-a2,
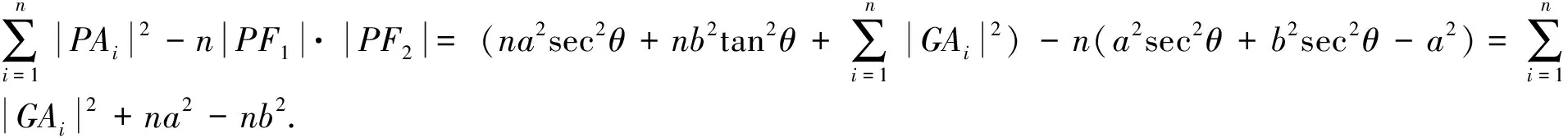

当A1,A2,…,An是空间内给定的n个点时,结论也成立,证明与平面情形类似.
定理3设G为平面(或空间)有限点集Ω={A1,A2,…,An}的重心,则以G为焦点的抛物线上的任意一点到A1,A2,…,An距离的平方和与该点到其准线距离的平方的n倍之差为定值.

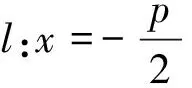
|PAi|2=(2pt2-xi)2+(2pt-yi)2


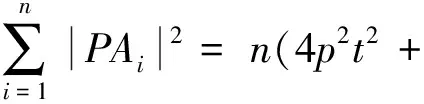
又由抛物线的定义知|PH|2=|PG|2=
所以有

当A1,A2,…,An是空间内给定的n个点时,易知结论也依然成立,证明同样与平面情形类似. 定理得证.
显然,本文的定理1、2、3中的椭圆、双曲线、抛物线上的任意一点均可分别推广到椭球面、双曲面、抛物面,限于篇幅,其证明留给感兴趣的读者.

