新型捕能消波浮式防波堤数值模拟与试验研究*
鲍灵杰,彭天好,黄方平,张 雷,林 躜
(1.安徽理工大学,安徽 淮南 232001;2.浙江大学宁波理工学院,浙江 宁波 315100)
随着现代港口建设不断向深水处发展,传统的防波堤越来越难以适应深水的条件。浮式防波堤作为一种新型防波堤结构,有利于水体的交换,对沉积物和生态环境影响较小,工程造价受水深影响小,地基适应性强,施工拆除相对方便,更适用于潮差大、土层松软的海域。因此,浮式防波堤具有广阔的应用前景[1-3]。
浮式防波堤结构多种多样,目前基本类型主要有浮筒式、浮箱式、水平板式等,为了提高浮式防波堤的消波效果,也有在基本结构形式上加以改进,通常采用増加反射面积、増设阻尼结构等措施。多浮箱式浮式防波堤与单浮箱式浮式防波堤相比,消波性能增加。沈雨生等[4-5]对双浮箱式浮式防波堤进行了二维波浪物理模型试验,分析了浮箱宽度、前后浮箱连接方式、前后浮箱间距以及浮箱入水深度等因素对浮式防波堤消浪性能的影响。嵇春艳等[6-8]结合风力发电、波浪能发电及消波的性能,采用STAR-CCM+数值模拟与试验相结合的方法研究了水轮机式浮式防波堤。汪宏等[9]针对柔性浮式防波堤对短波、长波均有较好掩护效果的优点,研究垂帘式浮式防波堤对短波、长波的良好消波效果。徐洪彬[10]研究得出相对宽度是影响浮式防波堤的主要因素,柔性浮堤的消波性能随相对宽度增加而明显减小,于相对宽度为0.3附近趋于稳定。陈俊华等[11-12]研究了在低流速潮流能下的发电装置桨叶的捕能性能并进行了结构优化。
国内外学者对于浮式防波堤的研究,大多通过相对深度、相对宽度等因素来分析浮式防波堤的透射系数、运动响应、消波机理等,并且savonius型桨叶大多用于风力发电、少部分用于低流速潮流能发电。而对于浮式防波堤应用于深远海智慧海洋牧场、实现能够自供给捕能的的消波性能研究较少。因此,本文研究新型捕能消波浮式防波堤的两种桨叶布置形式在捕能情况下的消波性能,评价浮式防波堤的综合性能,评价结果对于捕能消波浮式防波堤的设计具有一定的参考价值。
1 数值模拟试验
1.1 新型捕能消波浮式防波堤概况
新型捕能消波浮式防波堤包括savonius型桨叶组、HDPE浮管组。savonius型桨叶组按一定密度通过铁皮条系泊悬挂在HDPE浮管下,savonius型桨叶组之间亦通过空心轴连接在一起,形成网状阵列分布式发电系统;HDPE浮管组包括2根HDPE浮管及其连接支架,通过缆绳柔性系泊在桩基上。浮式防波堤见图1。
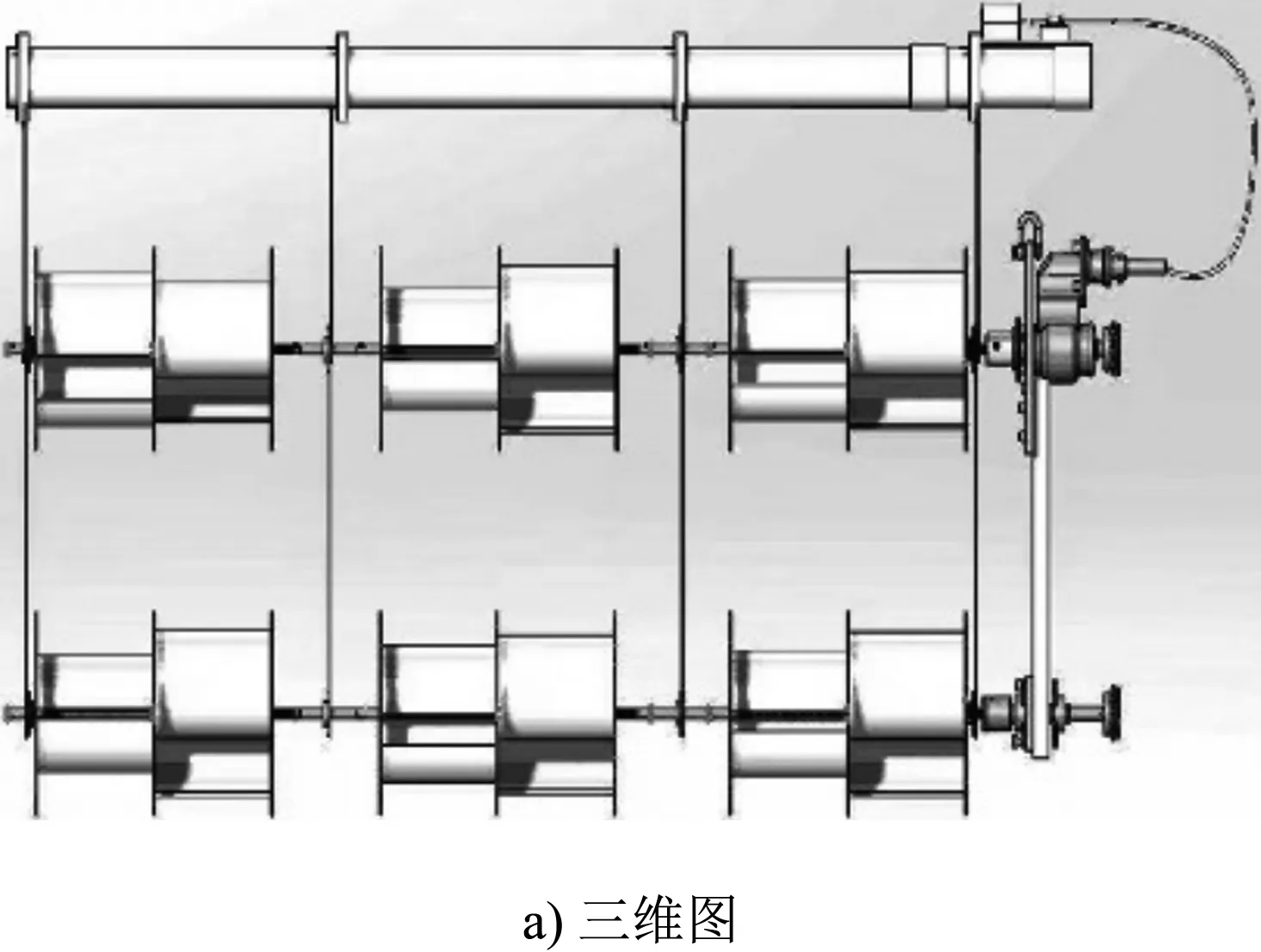

图1 浮式防波堤
参照工程背景实际情况和试验设备条件,模型按照1:5 的几何比尺进行设计。浮式防波堤的浮体几何参数为:浮筒直径0.33 m,浮筒间距0.65 m,浮筒与桨叶中心间距0.7 m,浮堤长度3 m,桨叶直径0.5 m,叶片半径0.15 m,桨叶高0.61 m。
1.2 控制方程
捕能消波浮式防波堤的数值模拟采用STAR-CCM+软件,假设流体不可压缩,黏性系数不变,控制方程为纳维-斯托克斯方程、自由液面方程和连续方程。沿x、y、z共3个方向的动量守恒[13]:
(1)
(2)
(3)
式中:ρ为流体的密度;t为时间;u、v、w为沿x、y、z方向的速度分量;p为流体压强;μ为黏度;S为边界条件。
1.3 湍流模型
在试验中,当波浪遇到浮式防波堤时,波浪会发生剧烈运动。RNGk-ε模型运用了重整化群的数学方法,计算中考虑了平均流动中旋转流动状况和小尺度影响。故本文模拟中选择RNGk-ε模型,其耗散率(turbulent dissipation rate)中的ε为:
(4)
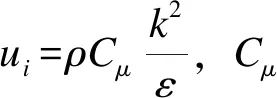
1.4 边界条件及初始条件设置
边界条件的设置为整个流域规划出一个区间,包括速度入口、压力出口、壁面。一般地,运动学的边界条件为:

(5)
(6)
初始条件主要是初始时刻自由液面的位置、速度场的分布、桨叶的初始速度等,研究周期性波浪运动时,初始条件不会影响稳定后的计算结果,但对计算量有一定的影响。
φ|t=0=f1(x,y),z=η(x,y,0)
(7)
(8)
1.5 网格参数设定
网格参数的设定主要包括网格基本尺寸和网格类型。数值模拟连续体网格模型选择切割体网格生成器及棱柱层网格生成器。为保证计算结果的精确性,在自由液面所能波动的范围内进行网格加密,一般加密3~4层以保证网格平滑过渡,网格随着与自由液面距离的增大而逐渐增大。同时,由于桨叶转动,采用了减运算的布尔操作,调用重叠网格的方式对减运算的网格和背景网格进行合理布局,网格数量大约为50万。网格划分见图2。

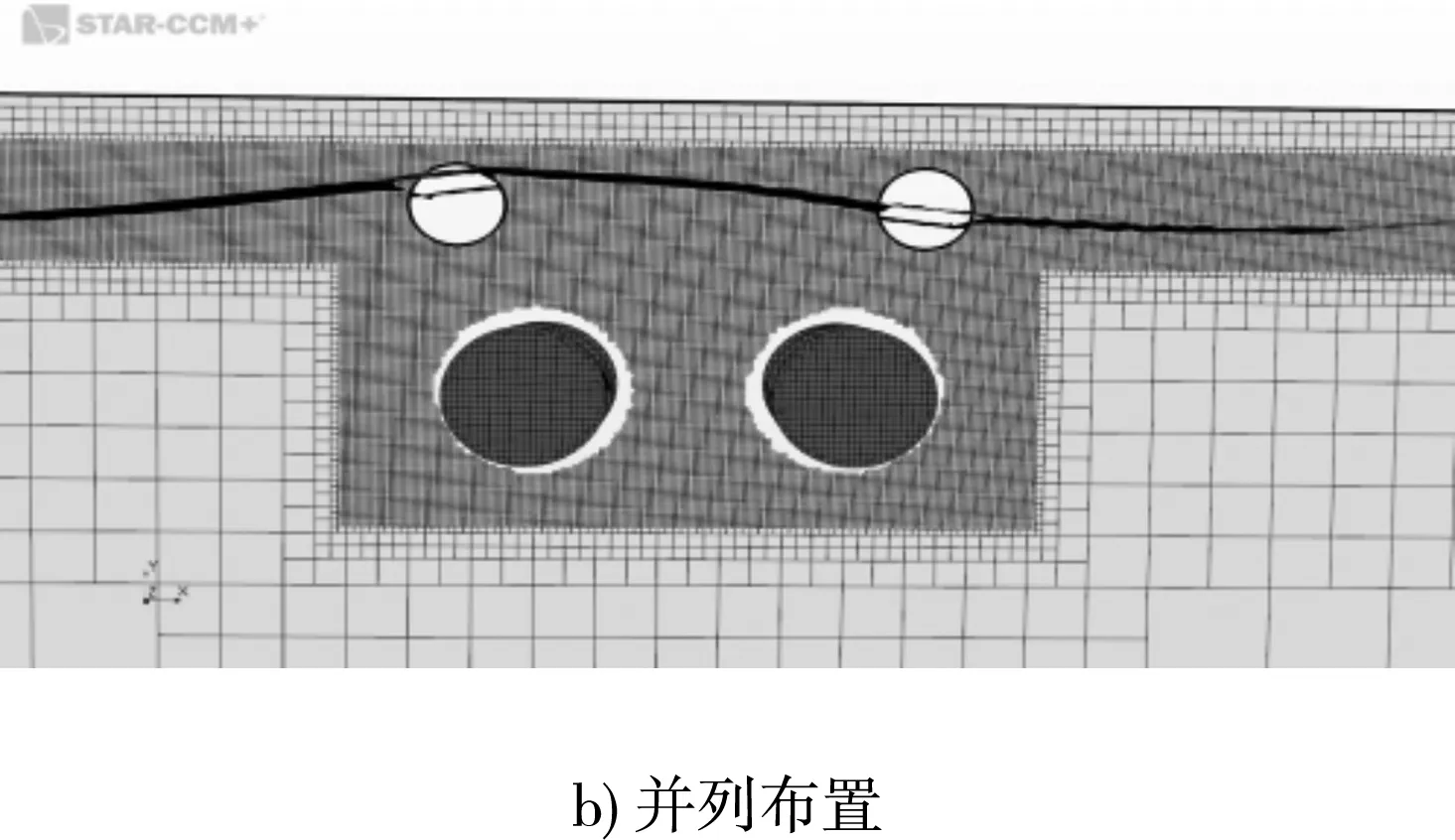
图2 桨叶网格划分
1.6 求解器参数设置
为提高计算精度,采用了二阶时间离散。时间步长的确定直接影响结果的准确性以及计算收敛等,时间步的确定与网格大小有关,根据经验公式Δt=T/(2.4n)确定时间步长,其中T表示造波的周期,n表示单位波长划分的网格数。停止条件设置包括最大迭代次数、最大物理时间等。最大迭代次数可根据结果的准确性进行调整,最大物理时间则根据计算结果及残差是否稳定等因素自行确定。
1.7 防波堤水动力模型
在笛卡尔坐标系下的新型捕能消波浮式防波堤的水动力模型配置,由双浮管和两组savonius型桨叶组成。为了满足浮体水动力计算的要求,简化求解过程,模型缩短了HDPE浮管长度及桨叶个数,把savonius型桨叶设置成与双浮筒相对位置固定且叶片轴线与坐标系x轴呈90°的形式。两种方案见图3。
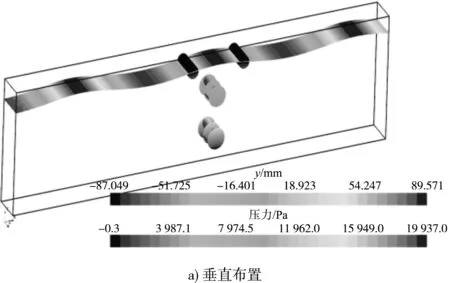

图3 桨叶水动力模型
模型选择三维、隐式不定常、欧拉多相流、湍流、状态多项方程、VOF波等。模拟介质包括水和空气两项,通过 VOF 模型捕捉自由液面。阻尼消波距离为波长的1~2倍。浮式防波堤水动力参数为:水深5 m,吃水深度1.7 m,HDPE浮体密度0.95 kgm3,桨叶排水量10 kg,桨叶惯性矩(0.337,0.337,0.16)kg·m2。
1.8 数值模拟及结果分析
为了简化模型、提高计算效率,忽略了浮式防波堤的六自由度运动,对浮式防波堤采用固定方式,桨叶则运用了STAR-CCM+的DFBI,开放了一个绕z轴旋转的自由度,桨叶在波浪作用下自由旋转,其数值模拟组次见表1。经过数字模拟计算,最大内部迭代5步,计算20 s以后数据趋于稳定,获得数据进行研究分析。根据STAR-CCM+获得的数据求平均值,平均转速、平均转矩见表2。
捕能消波浮式防波堤的两种桨叶布置形式获得的平均转速、平均转矩见表2。

表1 数值模拟组次

表2 两种桨叶布置形式的平均转速和平均转矩
数值模拟的桨叶所获得的功率为桨叶转动的平均转矩与平均转速的乘积,见图4。垂直桨叶布置捕获功率略大于并列桨叶布置的浮式防波堤。由于并列桨叶对于在波浪传递过程中2次消波,透射系数(图5)也比垂直桨叶布置的浮式防波堤小,消波性能略好。

图4 防波堤捕获功率

图5 防波堤透射系数
2 物理试验
2.1 试验条件
整个试验研究以70 m 长、4 m 宽、2 m深的试验水池为基础,试验总体方案见图6。摇板式造波机可产生波形稳定、可重复的规则波。桨叶通过传动装置传动,发电机当负载。传感器采集浮式防波堤的试验数据,主要测量仪器为波高仪、动态扭矩传感器。试验布置见图7。

图6 试验总体方案

图7 试验布置
2.2 试验设置
水池造出不同周期的线性波,系泊方式为多点张紧式,波高仪分别设置于浮式防波堤前后1~2个波长处。捕能桨叶入水深度为0.7 m,通过改变桨叶布置,分析不同桨叶布置的防波堤性能。考虑到初始波浪的撞击与破碎,采集时间在40 s以上,规则波试验的波浪数据采集时间间隔小于平均波周期的120,采集频率为50 Hz。在波浪稳定条件下,连续采集的波浪个数大于10个,并取其平均值作为代表值。
2.3 试验结果及分析
浮式防波堤试验通过模拟时变的波浪海况,测试浮式防波堤在整个工作周期前后的消波情况和捕能功率,综合评价该防波堤的两种桨叶布置形式在不同波浪周期下的水动力性能。
浮式防波堤悬挂的桨叶通过传动装置测得平均转速、平均转矩见表3,转速低于10 rmin以下的桨叶几乎不捕获有效的能量,只起到一定程度的消波作用。
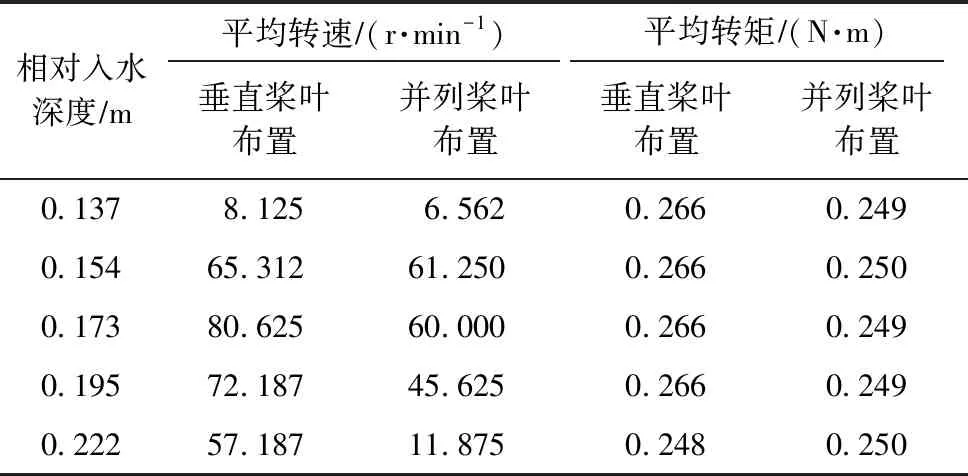
表3 传动装置测得的平均转速和平均转矩
捕获功率为所测得的平均转矩与平均转速的乘积见图8,由图8可知捕获功率随着相对入水深度逐步上升,再逐渐下降。由表3可知,引起功率大小变化的主要因素为平均转速,当转速较大时,功率也较大。

图8 防波堤捕获功率
透射系数为透射波与入射波的比值,透射系数越小则消波性能越佳。浮式防波堤透射系数见图9。桨叶并列布置消波性能优于垂直布置。
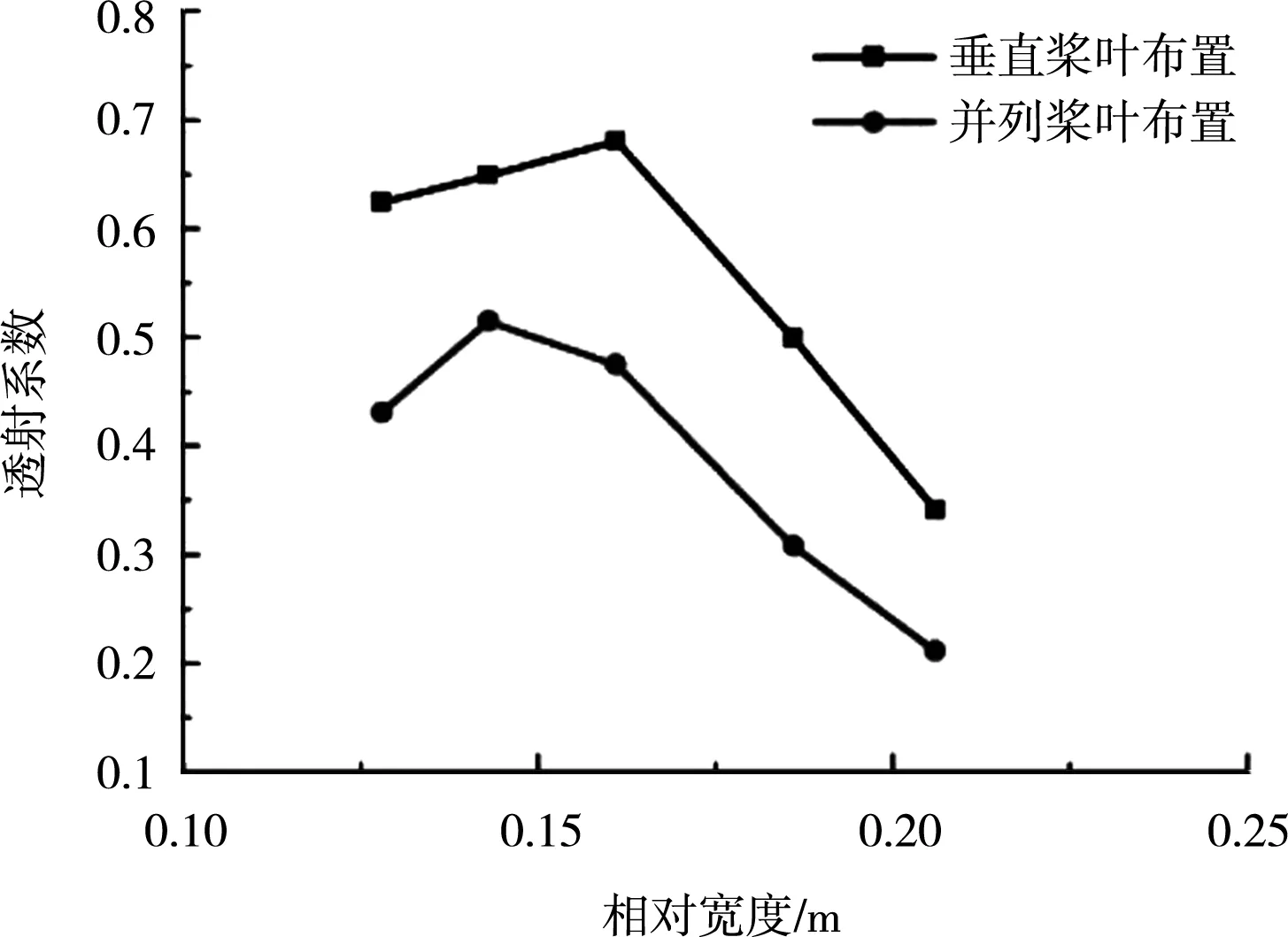
图9 防波堤透射系数
3 数值模拟试验与物理试验结果分析
由图4、8可知,在桨叶入水深度不变的情况下,捕获功率随着相对入水深度的增加先上升后下降。而相对入水深度为入水深度与波长的比值。波浪传播公式为:
v=λf
(9)
式中:v为波速;λ为波长;f为频率。当桨叶捕获功率较大时,从表4可知,桨叶的转动频率与波浪频率相近时,周期大约在1.6 s。

表4 频率比较
由图5、9可知,在防波堤宽度不变的的情况下,透射系数随着相对宽度的增大而略有上升,之后开始大幅度下降,符合大部分学者关于浮式防波堤的试验结果。总体来看,桨叶并列布置的的浮式防波堤消波性能优于桨叶垂直布置的浮式防波堤。
4 结论
1)对于新型捕能消波浮式防波堤的两种不同桨叶布置形式,当桨叶转动频率与波浪频率相近时,savonius型桨叶捕能效果较好,不同桨叶安装位置的防波堤会影响捕能效果的优劣,有进一步研究和应用的价值。
2)通过研究桨叶垂直布置和并列布置的浮式防波堤可知,两种形式的浮式防波堤波浪透射系数在0.20~0.75,从消波性能上看,两种浮式防波堤都有一定的消波效果,但是并列桨叶布置的浮式防波堤消波性能优于垂直布置的浮式防波堤。

