无梁板式高桩码头温度效应分析*
吴新云,何思远,2,刘智慧,戈国庆
(1.河海大学 港口海岸与近海工程学院,江苏 南京 210098;2.西安大略大学工程学院,加拿大 伦敦 N6A3K7;3.湖北省交通规划设计院股份有限公司,湖北 武汉 430051;4.山东省交通规划设计院,山东 济南 250031)
结构因温度变化而引起的应力,称为温度应力。混凝土结构温度变化主要由水化热、日照、气温及水温变化引起。水化热引起浇筑块早期温升、后期温降以及内外温差;日照引起结构向阳表面的局部温差;气温的日(昼夜)变化、寒流等由于作用时间较短,主要影响结构表面温差的梯度变化;气温的年变化[1]对结构物的影响是一种长期缓慢的作用,引起结构温度的均匀变化,使得结构产生变形和内力,称为结构的整体温差效应。铁路和公路桥涵、水工建筑物等相关规范一直重视温度作用分析,2012建筑结构荷载规范[2]专门增加了温度作用一章。
高桩码头是利用桩基将荷载传递到深层地基的靠船建筑物,上部结构为装配整体式结构时,结构段长度一般为60~70 m,分段处的缝宽可取20~30 mm。由于受到温度变化的影响,上部结构产生热胀冷缩,结构缝处混凝土起拱、挤碎、开裂、脱落等现象时有发生[3-5],有的甚至导致铁路钢轨上拱、扭曲而无法通车,不少桩和桩帽出现较严重的破损[6]。因此,研究高桩码头使用期温度作用很有必要。
事实上,整体温差的影响主要取决于工程区域年最高气温或者最低气温与结构完建竣工时气温的差值。研究表明,整体温差对高桩码头结构分段长度起控制作用[7-8],完建时气温对码头面板角点位移、上部结构内力和基桩受弯均有较大影响[9];整体温差作用下桩顶内力可能远大于水平静力、地震动力作用下的内力值[10]。何良德等[11-12]认为基桩对上部结构整体温差变形的约束作用可以忽略不计,基于上部平台的自由温变位移规律,提出了考虑高桩码头平动扭转的三维算法。
本文基于无限板的传热规律,结合杭州地区的逐时气象资料,对无梁板式高桩码头进行了年温度效应分析,研究了面板温差、变形和基桩位移、内力的变化规律,提出了合理确定基本气温的建议,给出了面板整体温差的估算公式。研究思路和方法可为梁板式高桩码头温度效应分析提供参考。
1 无限板的传热规律
x为板厚方向,板厚为δ,y、z方向为无限大。对于一维双向传热且不存在内热源且假定传导率是常数的情况下,热传导方程可表示为[13]:
(1)
式中:T为温度(℃);α为热扩散系数(m2s),α=k/(ρc),其中k为导热系数(W·m-1·K-1),ρ为密度(kgm3),c为比热容(J·kg-1·K-1)。
在相当多的情况下,初始温度可认为是均布的。常有3类边界条件,包括第一类温度边界条件、第二类热流量边界条件、第三类混合边界条件。假设无限板表面温度随时间t变化关系可用正弦曲线表示,该问题的初始条件T(x,0)和边界条件Ts为:
(2)
式中:T0为均匀分布的初始温度;Ti为边界初始温度;A为边界温度变幅;ω为圆频率,ω=2πp,p为温度变化周期。
不考虑辐射换热和对流换热,板内平均温度Tm(t)可表示为温差形式:
ΔT(x,t)=Tm(t)-T0=ξ(t)(Ti-T0)+
ζ(t)A+μAsin[ω(t-γ)]
(3)
式中:等式右边第1项为初始温度T0、环境温度Ti的瞬态传热问题解;第2和第3项为初始温度T0=0、环境温度依Ts=Asin(ωt)变化的周期传热问题解;ξ(t)、ζ(t)分别为随着时间而衰减到0的系数;μ、γ分别为准稳态时平均温度振幅(衰减)比、滞后的相位,是λ=δ2(αp)的函数。
无限板为钢筋混凝土材料时,取ρ=2 500 kgm3,c=920 J(kg·K),k=1.74W(m·K),α=75.7×10-7m2s。当δ=0.4 m、p=1 d时,板内平均温差比ψ=[Tm(t)-T0]A曲线见图1,经过2~3个周期后结构温度场会达到一个准稳定状态,此时ψ=μ=0.55。
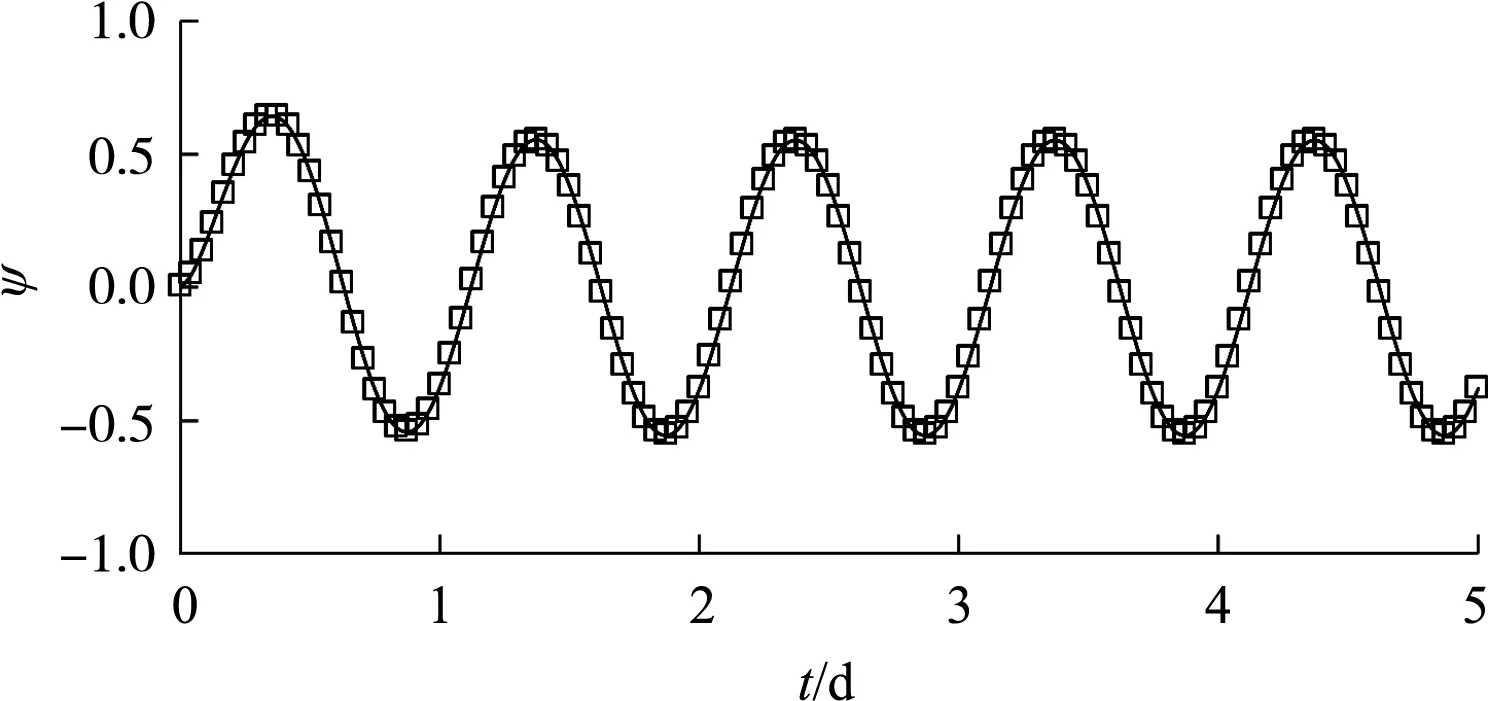
图1 板内平均温差比ψ曲线
结构处于空气中,气温通常随着日、年等作周期性变化。板内平均温度振幅比μ与板厚δ、环境温度周期p关系见图2,可以看出δ越厚、p越短则μ越小。δ≥0.3 m、p=24 h时,μ≤0.75,说明板厚较薄时,气温日变幅对结构的影响较大,是不可忽略的。p=360 d时,δ< 3.0 m、μ> 0.97,说明气温年变幅在结构内几乎是没有衰减的,可认为μ=1.0。

图2 准稳态平均温度变幅与板厚、周期关系
2 无梁板式高桩码头模型
2.1 工程实例
以浙江某电厂无梁板式高桩码头为例[14]。码头结构由面板、桩帽、基桩、靠船构件等组成。每结构段面板尺寸为59.7 m×22.5 m×0.4 m,横断面见图3。码头排架共14榀,间距4.4 m,每榀排架下布置7根预应力混凝土桩,海侧6根为400 mm×400 mm方桩,岸侧1根为400 mm×600 mm矩形桩,其中一对叉桩斜度为3:1,扭角为20°,结构段斜桩按八字对称布置。面板和桩帽采用现浇的C30钢筋混凝土,基桩为预制的C40预应力混凝土桩。
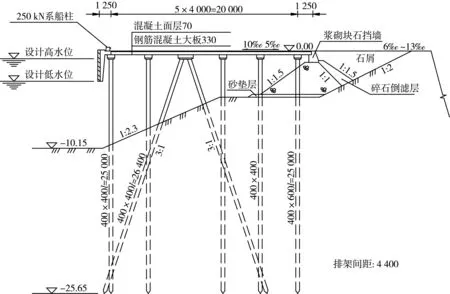
图3 码头结构断面(高程:m;尺寸:mm)
2.2 模型建立
由于结构段关于横轴对称,取一半结构段建立有限元模型,见图4。上部结构使用六面体单元划分,选用温度分析单元C3D8T;基桩采用梁单元,弹性嵌固点深度取5倍桩径。面板对称面施加法向约束和绝热处理;桩顶与桩帽进行耦合固结约束;桩底约束全部自由度。模型材料参数见表1。弹性模量参照JTS 151—2011《水运工程混凝土结构设计规范》[15]按混凝土强度等级取值,未考虑配筋率的影响。《水运工程混凝土结构设计规范》未给出热力学参数,水工、建筑混凝土结构规范仅给出了混凝土热力学参数,钢筋混凝土热力学参数按GB 50176—2016《民用建筑热工设计规范》附录[16]确定。

图4 码头结构数值模型
杭州位于东南沿海北部,处于中北亚热带过渡区,会出现明显的季节性变化,气温日较差大,根据《中国建筑热环境分析专用气象数据集》[17]相关软件,选取气象基准站(杭州)的典型气象年逐时气温数据。分析温度效应时,码头面板、桩帽考虑气温的影响,基桩不考虑温度传递。
2.3 时间步长
ABAQUS热传导瞬态分析[18]中,为了避免结果出现振荡,最小合理计算时间增量和单元大小之间的有如下关系:

(4)
式中:Δt为计算时间增量;Δl为模型典型单元尺寸。模型在面板厚度向典型单元大小取0.1 m,Δt> 2 203 s,取时间步长为1 h。
3 结果分析
3.1 气温变化特征
杭州地区典型年平均气温17.0 ℃,小时气温最高37.0 ℃、最低-2.4 ℃,日平均气温最高32.01 ℃、最低-0.67 ℃,气温可表示为年周期、日周期变化的函数:
Ts=Tam+Aacos[2π(t-τa)/pa]+Adcos[2π(t′-τd)/pd]
(5)
式中:Tam为年平均气温(℃);Aa、Ad分别为气温年振幅、气温日振幅(℃);t、t′分别为相对年零时、日零时的时间(h);τa、τd分别为气温年变化、日变化初始相位(h);pa、pd分别为气温变化的年周期、日周期(h)。
以小时气温、日平均气温、月平均气温拟合年温度变化,所得平均气温Tam、振幅Aa、最高气温Tmax、最低气温Tmin等特征参数接近,见表2,曲线比较见图5。

表2 典型年气温变化特征参数
注:带“*”为统计值,其余为推算值。

图5 日平均、月平均气温变化
7月平均气温Ta7=27.59 ℃、1月平均气温Ta1=5.20 ℃,可按下式简单估算Tam、Aa:
(6)
用30 d移动平均法可得Tmax=29.64 ℃、Tmin=3.91 ℃,可参照上式估算Tam、Aa。
取6:00、14:00作为日最低、最高气温出现时刻,可得1月、7月平均最高气温分别为8.64 ℃、31.64 ℃、平均最低气温分别为2.33 ℃、24.42 ℃。用30 d移动平均法可得最高气温6.89~34.32 ℃、最低气温1.23~25.92 ℃,与小时气温比较见图6。
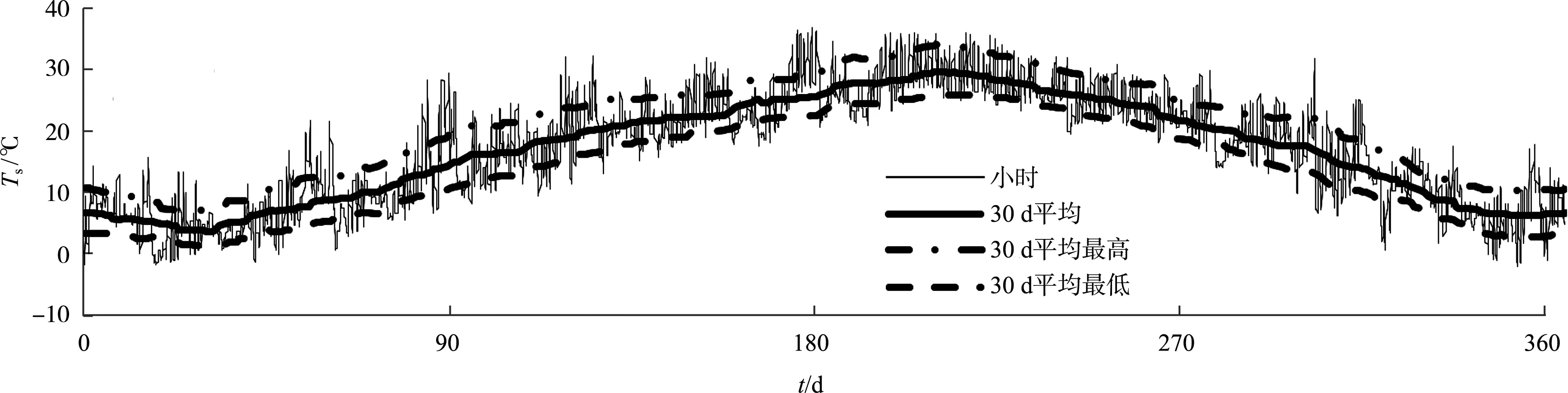
图6 平均最高气温与平均最低气温变化
3.2 面板温差场
面板的温度场主要还是受厚度方向上的传热控制,仅在距面板侧面约1倍厚度范围内受侧向传热的影响,其余部位水平向分布均匀,呈现一维传热特征。
分析表明,面板厚度内平均温度在第2 a开始进入准稳定状态,拟合的年温度曲线与气温变化一致,相位滞后γa=6 h,振幅几无衰减,μa=1.0。1 a内日平均气温变化见图7,平均日温差6.0 ℃,板内日温差3.3 ℃,衰减率μd=0.55,滞后γd=3 h。

图7 1 a内日温度变化
由以上分析可知,准稳态后面板内部平均温度可以表示为:
Tm=Tam+μaAacos[2π(t-τa-γa)/pa]+
μdAdcos[2π(t′-τd-γd)/pd]
(7)
式中:μa、μd分别为气温年振幅、气温日振幅在板内的衰减率;γa、γd分别为气温年变化、日变化在板内的滞后相位(h)。
假设码头上部结构竣工时,面板温度T0与初始气温Ti相同,则气温差ΔTs引起的面板平均温差ΔTm为:
ΔTs=Ts-Ti=Tam-Ti+Aacos[2π(t-τa)/pa]+
Adcos[2π(t′-τd)/pd]
(8)
ΔTm=Tm-Ti=Tam-Ti+μaAacos[2π(t-τa-γa)/pa]+
μdAdcos[2π(t′-τd-γd)/pd]
(9)
上式表明,面板平均温差呈周期性变化,春秋竣工时气温Ti越接近年平均气温Tam则ΔTm越小,而冬夏竣工时ΔTm越大。如1月1日零时竣工,面板的初始温度为4.8 ℃,最大温差为29.8 ℃,变化曲线见图8,可见大部分时间处于升温状态,ΔTm曲线的日周期振荡明显小于气温曲线的振荡(图6),另外也会出现与气温一致的骤降和陡升现象。

图8 1月1日零时竣工面板温差变化
3.3 结构变形与位移
某时刻码头面板变形见图9,图中上边缘为靠岸侧。面板变形(水平变形为主)云图呈规则圆圈状放大,位移矢量呈“发散发射”状。变形云图未出现局部凹凸区域,矢量图未出现“绕流”状区域。面板未发生无扭转,变形后依然保持直角,位移为零的发散中心位于靠海侧。


图9 码头上部平台变形
由热弹性力学可知,自由形变下面板平均应变与平均温差的关系为:
εm(t)=αtΔTm(t)
(10)
整理纵向(y)和横向(x)平均应变与平均温差关系可得:αxt=0.905×10-5℃-1、αyt=0.997×10-5℃-1,基桩的横向约束略大于纵向约束,但与给定的线膨胀系数αt=1.0×10-5℃-1相差9.4%以内,说明桩基对面板变形的约束作用可以忽略,面板处于自由形变状态。
面板位移与平均温差ΔTm(t)瞬时同步线性变化,岸侧角点的纵向位移变化曲线见图10,u2(t)=-0.294 6ΔTm(t),最大位移-8.78 mm,码头结构缝伸缩量将有2×8.78 mm=17.56 mm,该值可以用来指导结构段长度以及结构缝缝宽的选取。岸侧角点横向位移u1(t)=0.178 6ΔTm(t),水平合位移u(t)= 0.344 5|ΔTm(t)|,最大值10.26 mm。
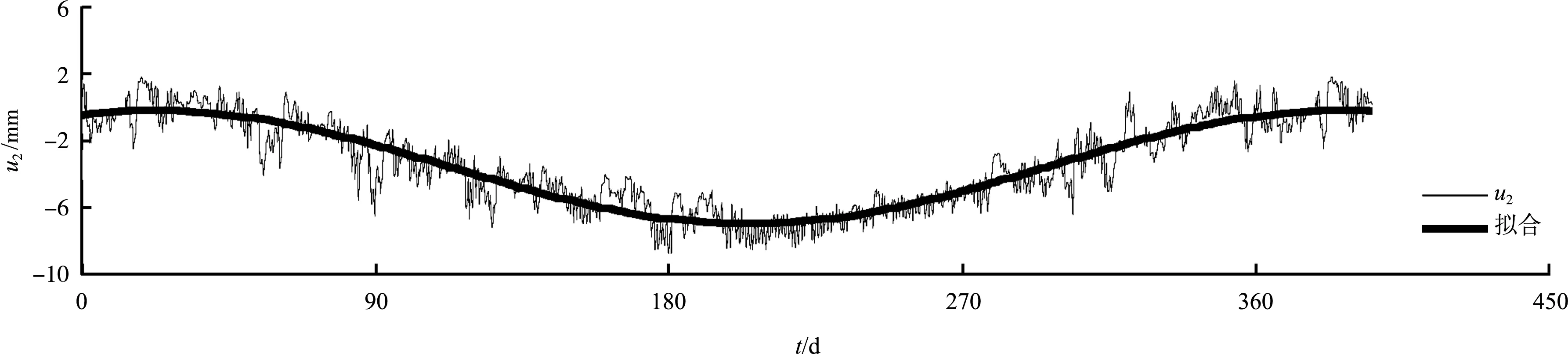
图10 面板岸侧角点纵向位移
气温对称作用于面板的上下平面,桩顶位移与其对应位置的面板位移相同。码头结构最不利桩一般出现在角桩,以岸侧角点处7号桩为例,桩顶水平合位移u(t)=0.321 2|ΔTm(t)|,最大位移9.57 mm,桩顶合剪力F(t)=1.209 6|ΔTm(t)|,最大剪力36.0 kN,桩顶合弯矩M(t)= 4.008 5×|ΔTm(t)|,最大弯矩119.3 kN·m。桩顶位移、内力分量也与面板平均温差ΔTm(t)瞬时同步线性变化,极值出现时间一致。
4 基本气温选取的讨论
基本气温是气温的基准值,是确定温度作用所需最主要的气象参数,目前还没有统一的确定方法。以杭州地区为例,基本气温见表3,不同规范的平均气温接近,气温振幅差异较大,最高、最低气温差异也大。目前,气温统计的样本有小时气温、日平均气温、月平均气温、月平均最高(最低)气温等4种,计算方法有取极值、多年平均值、一定年超越概率值等3种。欧洲规范、公路规范都取某气温的极值(最大、最小),欧洲规范的小时气温增幅显然要大于公路规范的日平均气温振幅,水工、铁路规范取7月、1月平均气温的多年平均值,建筑结构取50 a一遇的7月平均最高气温、1月平均最低气温,因此建筑规范气温振幅大于水工、铁路规范。
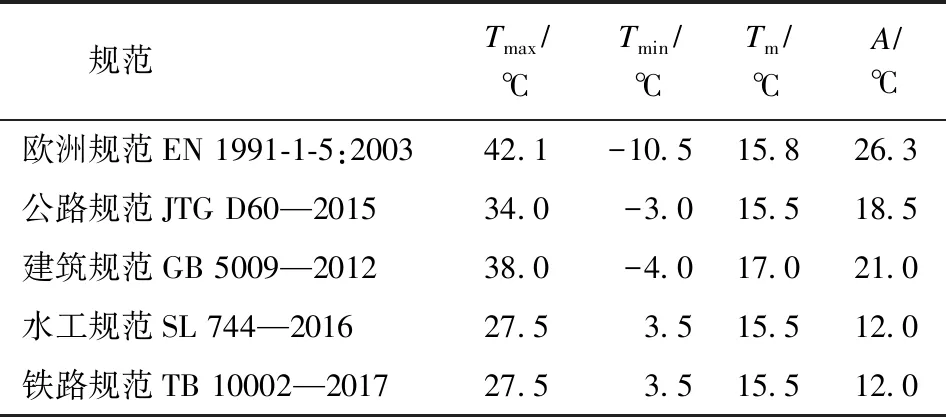
表3 杭州地区的基本气温
无梁板码头基桩的温度响应受面板的整体温差控制,两者瞬时同步变化。式(9)表明面板整体温差稍滞后于气温年、日极值获得,μa=1.0,因此整体温差的极值为:
(11)
式中:括号项Tam±Aa为不计日变幅影响的年最高气温Tmax、最低气温Tmin,可用7月、1月平均气温、或者30 d平均气温近似代替;Ad为气温日变化振幅,可分别用7月的平均最高气温与平均气温差、1月的平均气温与平均最低气温差表示,或者用30 d平均最高气温、平均气温、平均最低气温差代替。
水工结构尺寸一般较大,气温日变化影响较小,可近似假设μd=0.0,用月平均气温代表年气温极值,式(11)可简化为:
(12)
由上式可见,水工规范取7月、1月平均气温为统计样本是合理的。无梁板式高桩码头上部结构处于空气介质中,面板上下面外露且厚度较小,气温日变化影响较大,近似假设μd=1.0时,式(11)可简化为:
(13)
由此可见,无梁板式高桩码头的气温日变化不可忽略,统计样本如取小时气温可能高估气温骤降或骤升的影响,如取日平均或月平均气温并不能反映气温日变化的影响,可取7月平均最高气温、1月平均最低气温,如杭州典型气象年统计值分别为31.64 ℃、2.33 ℃,获得多年的统计样本后,按一定年超越概率确定基本气温。
因此,无梁板式高桩码头基本气温可按建筑规范方法确定,另外可根据工程经验及当地极值气温与月平均最高和月平均最低气温的差值,酌情对基本气温进行修正。对于梁板式高桩码头,面板以下的纵梁、横梁尺度相对较大,μd值大小及其影响规律、基本气温的合理确定等问题,值得深入研究。
5 结论
1)气温可表示为年周期、日周期变化的函数。在无梁面板中呈现以厚度方向为主的一维传热特征,温度场在水平向分布均匀;气温年变幅在面板内几无衰减,日变幅对面板温度影响不可忽略。
2)面板的整体温差与竣工时气温、年平均气温差,以及年变幅、日变幅的衰减值有关。应尽量避免酷暑、严寒气候下施工闭合,以削弱结构的温度响应。夏季宜选择晚上降温段、冬季宜选择白天温升段施工闭合,可减小气温日变化的不利影响。
3)无梁板码头基桩的温度响应受面板的整体温差控制,两者瞬时同步变化。建议参照建筑荷载规范取50 a一遇的7月平均最高气温与1月平均最低气温作为基本气温,合理确定面板的整体温差。
4)在日照作用下,混凝土结构与外界的热交换,不仅有来自太阳辐射的热流,也有与周围坏境的对流和辐射热交换。日照对高桩码头的温度效应影响,有待进一步研究。

