波浪非线性对斜坡堤透浪特性影响研究*

丁 坤,冯 曦,马钢峰，冯卫兵

(1.河海大学 港口海岸与近海工程学院，江苏 南京 210098；2.欧道明大学 土木与环境工程学院，弗吉尼亚州诺福克 美国)

常见的防波堤通常由采石场的石头或人工块石构成，具有渗透性。堤前的波浪通过防波堤的堤心石孔隙渗入堤后，减少了堤前反射，但在堤后产生了次生波，影响港内的泊稳条件，尤其是在长周期波浪区域内，由于长周期波浪波能较大，穿透性强，且在堤后港区内不易衰减，对港池有非常大的影响，因此，需要对防波堤的透浪特性进行深入研究，从而了解其透浪机理。针对这一主题，国内外进行了大量研究[1-6]。普遍认为，当波浪穿过防波堤时，在防波堤内部与堤心石产生相互作用，损耗了部分能量导致波高减小，防波堤透浪特性取决于防波堤的物理特性如堤心石粒径、孔隙率、堤身宽度等以及波浪特性如波高和周期等。然而，目前国内外关于不越浪斜坡堤透浪特性的研究并不是很多，主要是对出水堤和潜堤(包括块石或人工块体护面)的稳定性与消浪规律[7]、物模试验的比尺效应[8]、堤内压强分布及变化规律[9]、堤心石的级配选择[10]等方面进行了一定的研究。虽然关于斜坡式防波堤的透浪特性方面有很多研究，但针对不越浪情况的研究还比较少，此外，考虑波浪特性尤其是波浪非线性对斜坡堤透浪特性影响的研究也较少。目前国内外研究提出的关于(不考虑越浪情况)斜坡堤透浪系数的经验公式主要有：斯蒂芬森[11]通过理论分析和简化得出的透浪系数公式，习和忠[12]从波浪波能传递入手推导出波高在堤内衰减规律的理论公式，Ahrens[13]、王登婷[14]、葛晓丹[15]、冯卫兵、杨会利[16]等分别通过物理模型试验拟合得到的透浪系数计算公式,但这些公式都没有考虑厄塞尔指数这一因素，且各个公式计算得出的透浪系数差别较大。

所以，本文的主要目的是：1)研究波浪特征对不越浪斜坡堤透浪特性的影响；2)通过数模的方式扩展数据集，以便进行更进一步的分析和验证；3)拟合出合适的透浪系数经验公式。

1 方法

1.1 物理模型

一个典型的不越浪斜坡堤透浪试验在河海大学海工实验室的波浪水槽内进行，水槽有效长度80 m、宽0.5 m、高1.8 m，水槽前后端都设置了消能缓坡，以减小波浪传至前后端时所产生的反射。从国内外关于防波堤堤心石模型比尺效应的研究成果可以知道，为了尽量消减由黏滞力不相似而引起的流动流态特性不相似的影响，采用比尺较大的物理模型是相对有利的。因此应该尽可能选择较大的模型比尺，但同时要综合考虑实验室仪器设备和堤心石试验样本材料的选择等。因此，按照重力相似原则，本物理模型试验选取了1:30的模型比尺。

斜坡堤采用抛石斜坡式结构，堤前迎浪面放置扭王字块体，坡度为1:1.5，护面块体不规则摆放，堤心石由中值粒径d50=0.014 m、孔隙率n=0.45的不均匀块石组成。堤前后共布置6根用于测定波浪沿程衰减的浪高仪，并通过DJ800型多功能监测系统对波高进行采集分析。防波堤模型断面尺寸、波高仪位置见图1、2。试验所用的波要素：堤前水深40 cm，波高范围5～20 cm，波周期1.1～2.3 s，波要素见表1。

图1 防波堤模型断面结构和波高仪布置(单位：cm)

图2 模型摆放情况

表1 试验波要素

注：采用的模型比尺为1:30。

1.2 数学模型

基于NHWAVE模型模拟了该物模试验。NHWAVE模型是基于体积平均-雷诺平均-纳维-斯托克斯方程(VARANS)[17-18]建立的三维动压模型，可以用于模拟动水压力、自由表面、旋转流等。NHWAVE模型通过添加了附加阻力项的VARANS方程对可渗透防波堤[19]进行建模：

(1)

(2)

式中：i,j=1,2,3;x*i为笛卡尔坐标系；t*为时间;ui、uj分别为x*i和x*j方向的速度分量；n为有效孔隙率；p为总压强;ρ为水的密度；gi为引力；v为层流运动黏度；vt为湍流运动黏度；R为附加阻力系数。

式(2)的最后一项为可渗透防波堤中附加阻力项，其中附加阻力系数R的公式为:

(3)

(4)

式中：ap为线性阻力系数；bp为非线性阻力系数；cp为多孔介质中加速流体的附加惯性系数。这些系数的公式为:

(5)

(6)

(7)

(8)

式中:D50为多孔材料的特征直径(m)；T为波周期(s)；n为有效孔隙率；ν为运动黏度，γ为与加速度参数AC=|U|/(nTg)有关的经验系数，通常取0.34[20]；α、β为待定的经验系数。

当数值模拟的结果可以较好地和试验结果相对应，模拟防波堤透浪特性的的数学模型被建立。式(5)、(6)中的待定经验系数α、β和堤心石的级配、高宽比、形状(粗糙度，表面纹理)以及块石相对于平均流动的方向有关[21]，经过不同的α、β组合测试，本文选用的α、β为200、0.45。建立的网格尺寸为0.02 m×0.02 m，因此，建立了4 000个横向网格，即意味着每个波长的长度有80～200个网格，时间步长为0.01 s。模型的边界条件基于物理模型的设置，在模型的末尾放置10 m宽的海绵层用于防止波浪反射。

利用bias和离散指数SI进行模型的验证，其公式如下：

(9)

(10)

式中：N为数据个数；Hmodel为数模模拟出来的波高；Hexp为物模试验测得的波高。

图3是在波高10 cm、周期1.9 s的波浪作用下各测站的自由表面的对比，并采用相关系数R和均方根误差RMSE来对比验证。图4是不同波要素的规则波作用下数学模型(横坐标)和物理模型(纵坐标)的堤后波高的对比，通过bias(左上)和离散指数SI(右下)进行验证，结果表明防波堤的透浪过程可以被NHWAVE模型较好地模拟。

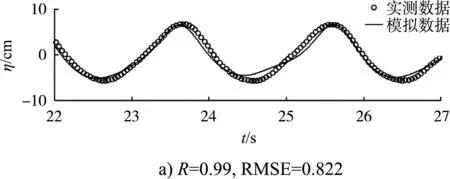
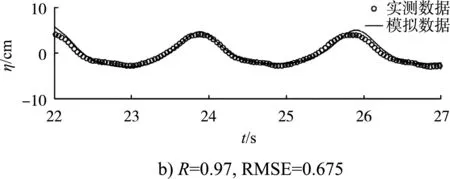
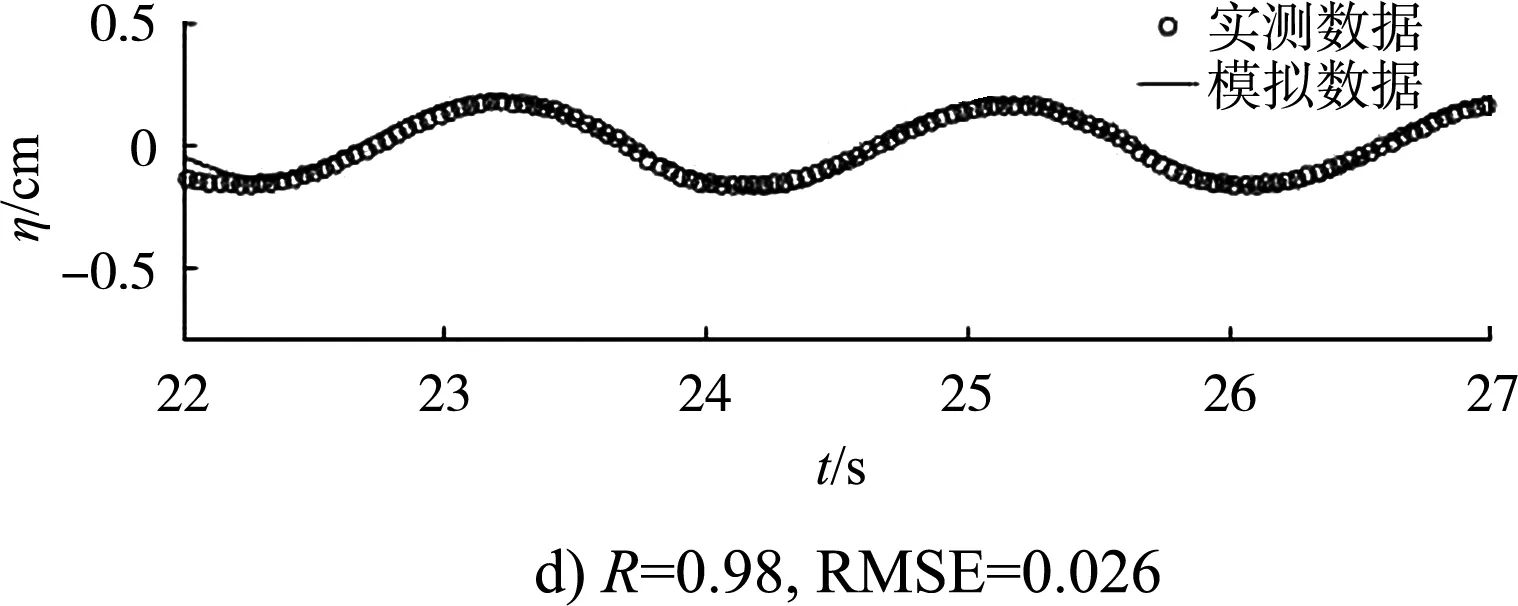
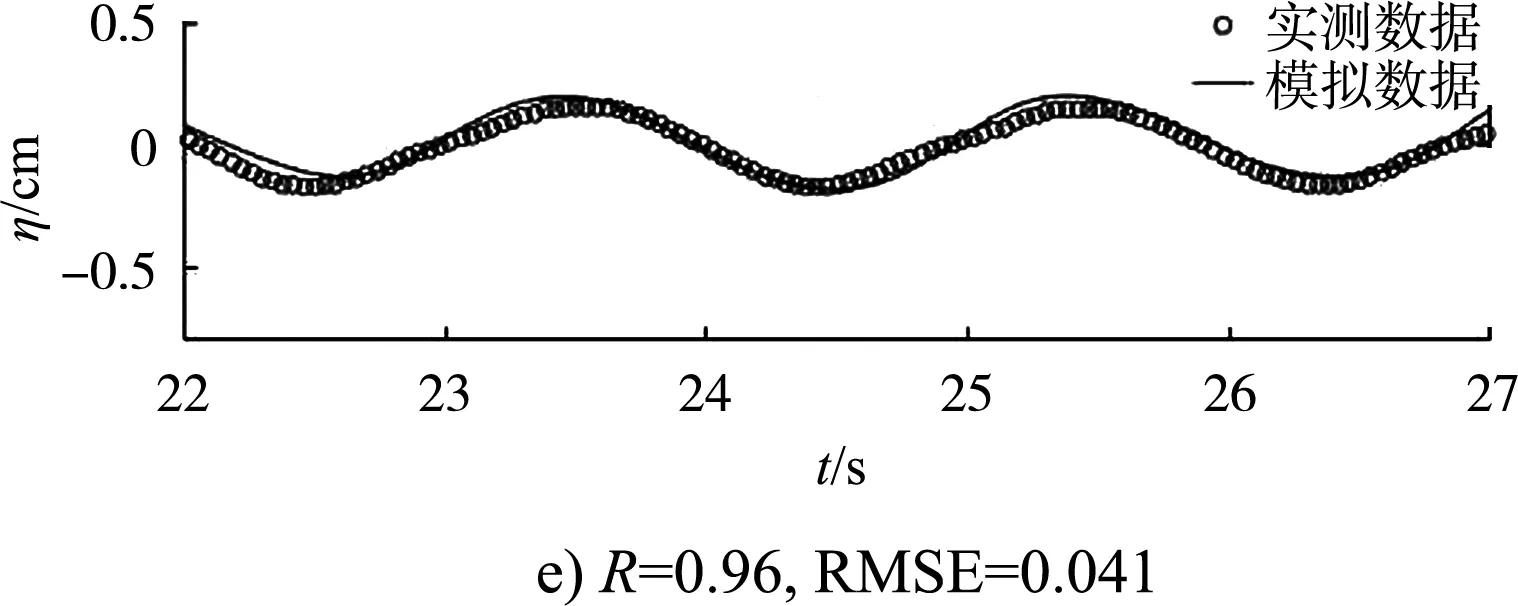
图3 规则波作用下防波堤前后6个测站的数学模型数据与物理模型数据的对比

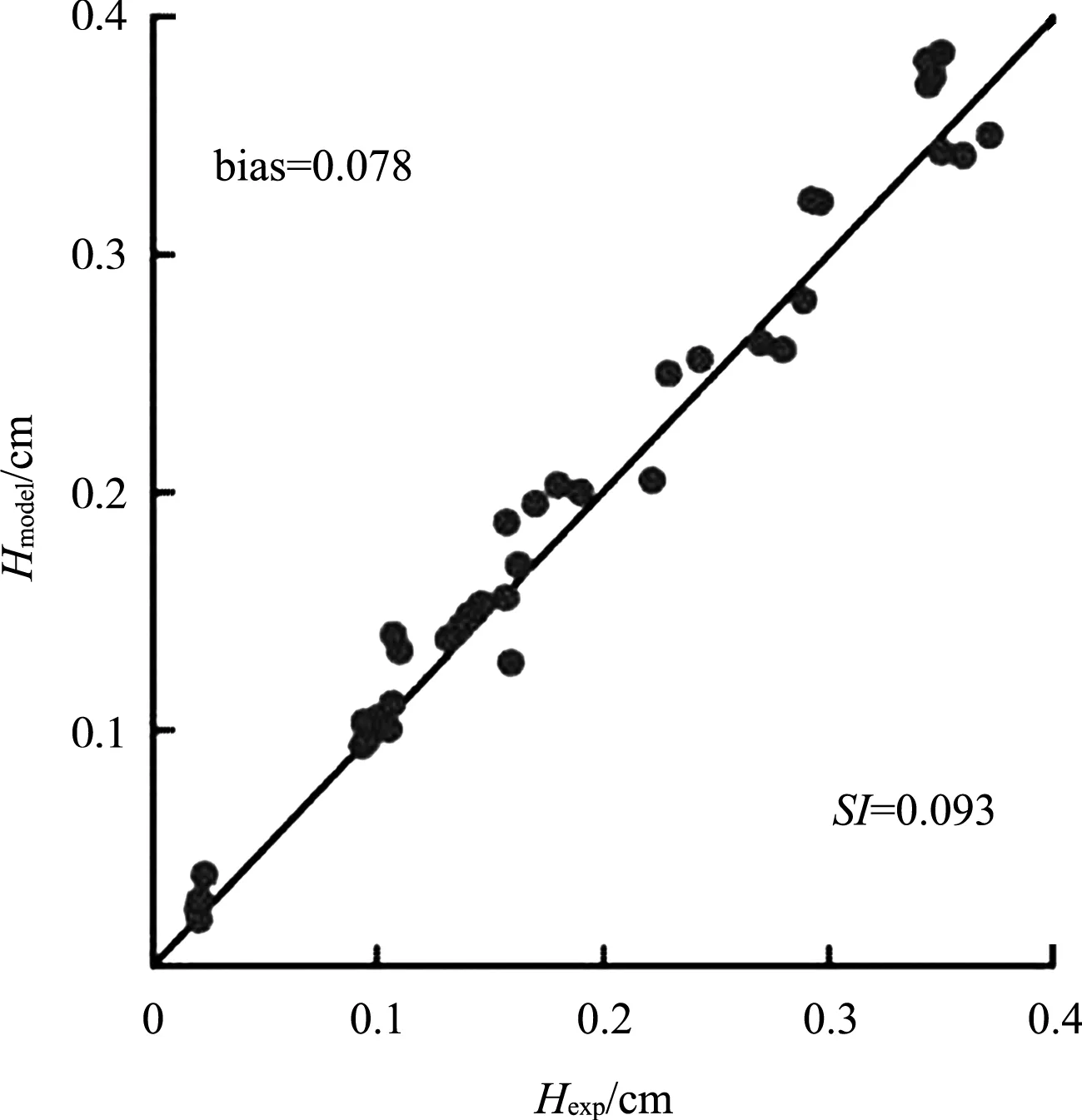
图4 规则波作用下的数学模型与物理模型数据的验证

1.3 试验数据

采用数学模型增加了物模试验的堤前水深、堤心石粒径和波要素等因素的试验组次，见表2。

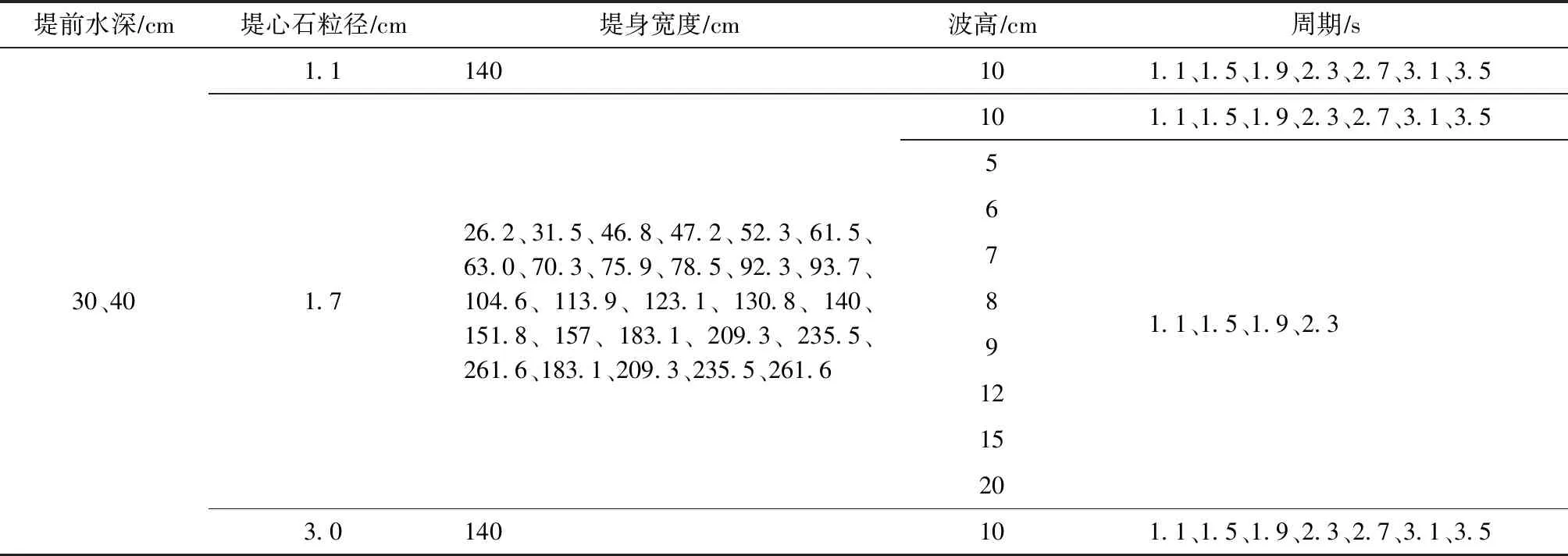
表2 数模试验设置

2 试验结果与分析

2.1 堤心石粒径对透浪特性的影响

在文献中，斜坡堤透浪特性通常使用堤后透浪系数(Kt)来表示。它是通过绝对长度堤身宽度(B)后的堤后波高Hx与入射波高Hi的比值：

(11)

斜坡堤对透浪特性的影响可以通过不同堤心石粒径d50(小粒径1.1 cm，正常粒径1.7 cm，大粒径3 cm)下的透浪系数来反映。图5给出了堤身宽度为140 cm时，在10 cm波高、不同波周期的规则波以及不同堤心石粒径作用下的堤后透浪系数Kt。从图5可以看出：随着波周期的增大，堤后透浪系数Kt随之增大，即周期越大，波浪越容易通过防波堤传入堤后水域影响堤后港池的泊稳条件。堤心石粒径越小，防波堤消浪效果越好。就中值粒径为3 cm的堤心石而言，当波周期为1.1 s时，波浪衰减了99.7%；当波周期为3.5 s时，波浪只衰减了84%，周期增加了2.4 s，波浪衰减幅度为15.7%。对于中值粒径为1.1 cm的堤心石，在周期为1.1 s时，波浪衰减了99.9%；当周期增加到3.5 s，波浪衰减为90%，波浪衰减幅度为9.9%。这表明周期越大，堤心石粒径的大小对堤后透浪系数的影响越大。当工程区域内的波浪周期较小时，堤心石粒径的选择对于防波堤透浪特性的影响不大，工程区域内的波浪周期过大时，不宜选用大质量范围的块石来作为防波堤的堤心石。

图5 规则波作用下透浪系数随周期和堤心石粒径的变化

2.2 相对堤宽对透浪特性的影响

前文都是采用固定绝对长度堤身宽度(B)的情况下得到的透浪系数Kt，而防波堤的透浪特性不仅取决于防波堤的物理特性如堤心石粒径、孔隙率、坡度等，而且和入射波的波要素有关，如长波、短波、大波、小波等。因此，为了在斜坡堤透浪过程中考虑更多的物理因素，提出了采用相对堤宽(B/L)不变情况下的透浪系数KL。这样可以更容易解释波浪特性对斜坡堤透浪特性的影响，有效的堤后透浪系数定义为：

(12)

式中：HL为通过相对堤身宽度后的波高；Hi为入射波高。

图6是在相同周期、不同波高下的透浪系数KL和相对堤宽(B/L)的关系。可以看出，堤后透浪系数随着相对堤宽增大而减小，且波高越大则波浪在防波堤内衰减得越厉害，反之亦然。例如，对于入射波高为5 cm波浪，在0.1倍波长的堤身宽度下，波高衰减了81.3%；当堤身宽度增加到0.4倍波长，波浪衰减了96.1%，3倍的堤身宽度的增加使波浪多衰减了15%。但在波高为15 cm、堤身宽度为0.1倍波长的的情况下，波高衰减了90.2%；当堤身宽度增加到0.4倍波长，波浪衰减了98.6%，3倍的堤身宽度增加仅使波浪多衰减了8.4%。这表明具有相同周期的波浪，波高越大，随着相对堤宽的增大，衰减的幅度越小。值得一提的是，当堤身宽度达到0.4倍波长时，透浪系数变化幅度开始减小，当堤身宽度达到0.8倍波长以上时，透浪系数几乎为一个恒定值。这意味着堤身宽度达到一定倍数的波长时。透浪系数不再取决于堤身宽度。

图6 规则波作用下透浪系数随相对堤宽和波高的变化

2.3 波浪非线性对透浪特性的影响

基于相对堤宽(B/L)确定的波浪透射系数，表明了斜坡堤的透浪能力取决于波浪的特性。从这个意义上来说，研究波浪透浪过程需要一个全面的指标来反映波浪特性。文献大多数对斜坡堤透浪特性研究通过4种假设来简化：1)斜坡堤堤身是稳定的；2)波浪是规则波；3)堤心石较为规整；4)波浪遵循线性理论。总体而言，波浪特征尤其是波浪的非线性对于斜坡堤透浪的影响没有引起足够的重视。在这一节里，厄塞尔指数和波陡被用来研究波浪非线性对斜坡堤透浪特性的影响。厄塞尔指数定义为：

(13)

式中：Hi为入射波高(m)；h为堤前水深(m)；L为波长(m)。

图7是对于不同相对堤宽下，透浪系数和厄塞尔指数的关系。可以清楚地看到，在相同周期下随着厄塞尔指数的增加，KL随之减小，这意味着波浪非线性越强则防波堤透浪特性越弱。此外，波浪非线性对于斜坡堤透浪特性的影响也取决于周期和相对堤宽。例如，当堤身宽度为0.2倍波长、周期为1.1 s时，厄塞尔指数增加到50时KL几乎达到了0值，也就意味着在此波况条件下，波浪无法透过防波堤。此外，当堤身宽度为0.2倍波长、周期为1.5 s时，厄塞尔指数须增加到110时KL才达到了0值。当周期为1.1 s、堤身宽度为0.4倍波长时，厄塞尔指数仅须增加到20时KL就达到了0值。

图8是不同的相对堤宽下透浪系数和波陡的关系。可以看出随着波陡的增加，KL随之减小。并且当波陡增加到0.005时，KL的变化幅度开始减小；当波陡大于0.01时，KL似乎获得一个恒定值。这意味着防波堤的透浪特性不再取决于波陡。此外，波陡对于斜坡堤透浪特性的影响也取决于相对堤宽。因此，如图7所示，堤身宽度为0.2倍波长时，波陡从0.001增加到0.01，透浪系数减少了12%(KL从0.167减小到0.047)；然而在堤身宽度为0.4倍波长时，波陡从0.001增加到0.01，透浪系数仅减少了6.6%(KL从0.072减小到0.006)。

图7 规则波作用下透浪系数随厄塞尔指数的变化

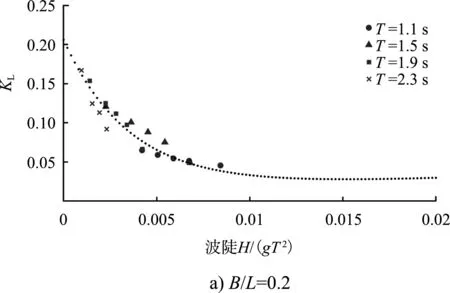
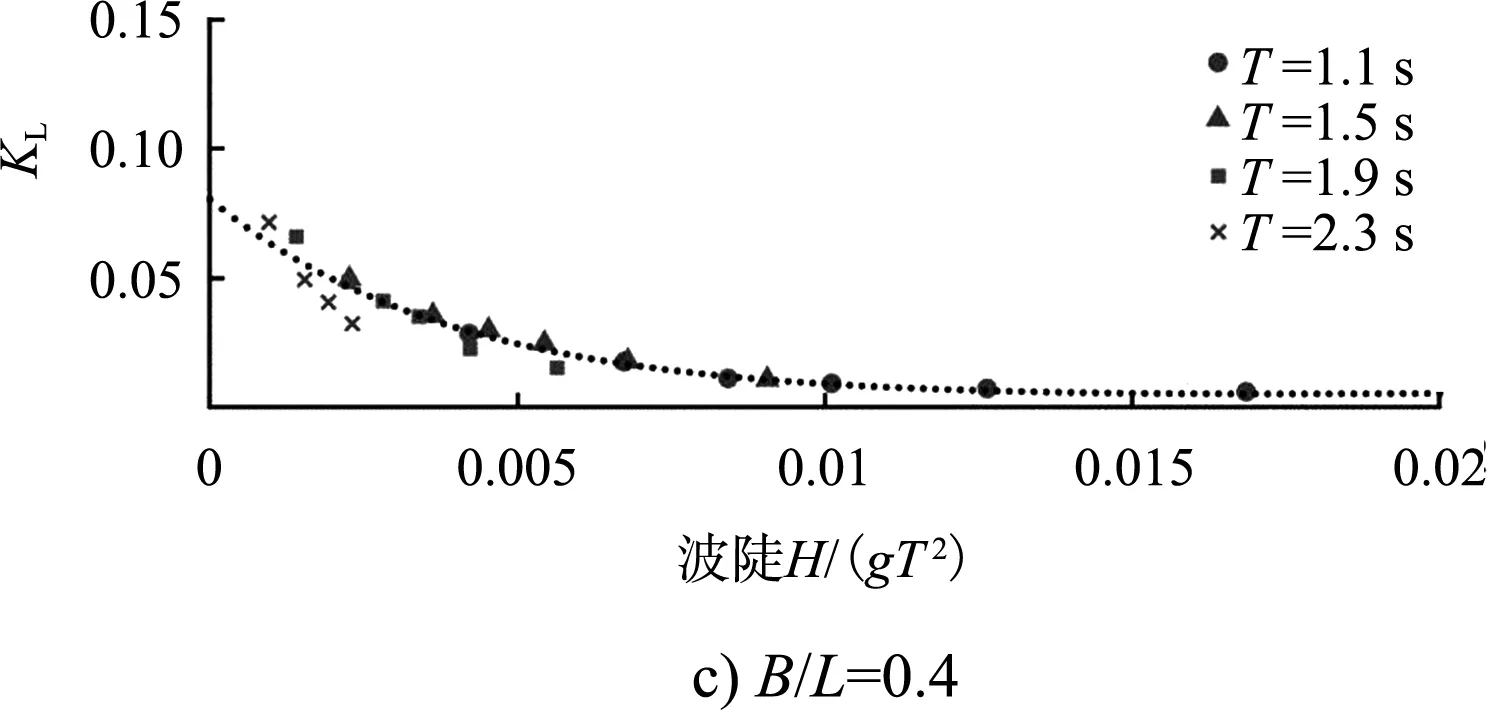
图8 规则波作用下透浪系数随波陡的变化

2.4 经验公式拟合

综上分析可知，在规则波情况下，透浪系数与波浪非线性相关，在较小周期波浪作用下受堤心石粒径影响不大。因此，基于冯卫兵等的研究成果，引入无量纲因子相对堤宽B/L、厄塞尔指数HL2h3、波陡H/(gT2)，其中B为静水面处堤身宽度，L为波长，H为入射波高，T为入射波周期，h为堤前水深。本试验堤前水深为0.3、0.4 m，g为重力加速度，因此一个特定粒径下的透浪系数Kt可表示为：

(14)

根据透浪系数Kt与各无量纲化因子之间的幂函数关系，将透浪系数公式设为：

(15)

式中：β、α1、α2、α3为待定系数。对式(14)两边取对数得：

(16)

采用多元线性回归法[22]计算得到式(15)中的待定系数，然后将得到的透浪系数经验公式的计算结果与物模试验结果进行对比分析，再对系数进行校对，最终可以得到规则波情况下的透浪系数计算公式：

(17)

透浪系数经验公式(16)的计算结果与物模试验值的对比见图9，其相关系数R2为0.933。对透浪系数计算值与试验值的绝对误差和相对误差进行计算，结果见表3。可以看出，在规则波情况下，计算结果与试验结果拟合效果是较好的。

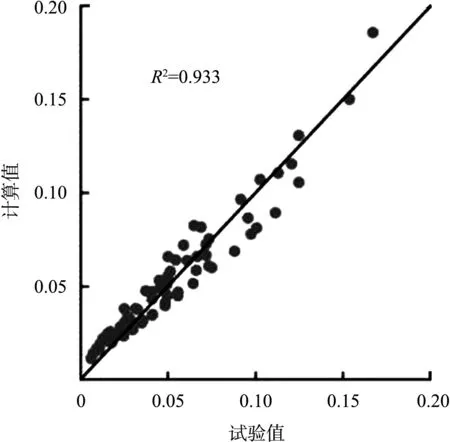
图9 透浪系数Kt计算值与试验值的对比

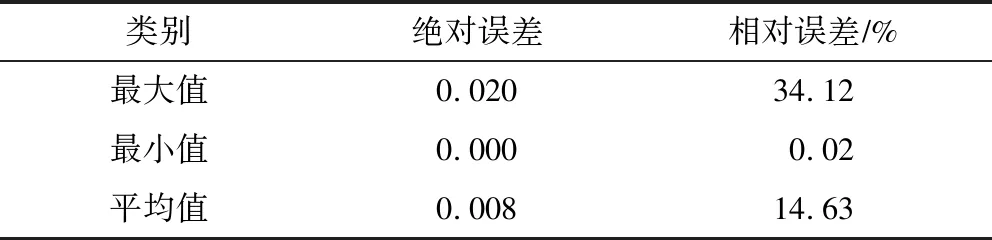
表3 透浪系数Kt计算值与试验值误差

3 结语

1)在规则波作用下，堤后透浪系数随波周期增大而增大，当周期较小时，堤心石粒径的选择对透浪系数影响较小，而当在较长周期波浪作用下，则无法忽视堤心石粒径的影响。因此，在实际工程中堤心石粒径的选择需要经过验证后方可应用到工程。

2)相同周期下的有效透浪系数随着厄塞尔指数的增加而减小，即波浪非线性越强则波浪透过防波堤的能力越弱。此外，波浪非线性对斜坡堤透浪特性的影响还受相对堤宽和周期的影响。

3)规则波作用下，有效透浪系数随着波陡的增加而减小。无论相对堤宽如何变化，都可以看出波陡在0.001～0.01时，对透浪特性有很大影响，当波陡大于0.01时，透浪系数与波陡无关。这表明，当波浪特性(波陡表示)和堤心石粒径已知，就可以得到堤后的透浪系数。

4)在相同周期的规则波作用下，堤后有效透浪系数随着相对堤宽增大而减小，且波高越大，波浪在防波堤内衰减得越厉害,反之亦然。当堤身宽度达到0.8倍波长以上时，不越浪斜坡堤的透浪特性与堤身宽度无关。

5) NHWAVE模型可以很好地模拟物理模型中所观测到堤后的波高变化，并拓展了斜坡堤透浪试验的数据，得到不同波要素下0.1倍波长到1倍波长的堤身宽度的透浪系数。在此基础上，一个特定堤心石粒径下的堤后透浪系数可以表示为厄塞尔指数、相对堤宽和波陡的函数。