基于多目标遗传算法的电机噪声优化
张 耀,杜荣法,赵新超,叶乾杰
(卧龙电气驱动集团有限公司,上虞 312300)
0 引 言
对电机进行设计优化,降低成本、提升性能,无疑可以提升产品的市场竞争力。但是随着电机的振动噪声性能、转矩密度、功率密度、恶劣环境抗退磁等指标的提升,以及开发周期逐渐缩短,这就要求我们在确保成本的前提下,以最短的周期设计出性能优良的产品。
以往的电机优化方式是先对电机某一参数(如槽口尺寸)实施优化,待其性能达到最优,再逐步优化其他参数,最后获得所有拓扑结构参数都已优化的电机[1]。这种优化方式未考虑到电机不同结构尺寸参数之间互相影响,并且电机性能是不同参数组合优化的结果,优化另一参数时,之前得到的最优解可能发生偏移,而且这种方法需要大量的手工迭代操作。
田口法[2-3]是一种应用广泛的局部优化方式,通过正交表的创建,能以较少的试验次数组合得出多目标优化设计时不同设计参数的最佳方案。但是其缺点也与其他局部优化方法相同,初始点的选取非常关键,只能在初始选取点的附近进行求解,所以其全局优化能力变差。
遗传算法[4-6]作为一种智能型随机搜索算法,具有非常强的全局寻优能力,它最明显特点是内嵌并行性及全局解空间优化。基于其优良特性,遗传算法已在电机工程领域得到推广。
1 基于遗传算法的多目标优化方法
1.1 多目标优化思想
多目标优化算法是数学规划的分支之一,是研究多个目标在相对一定区域最优化问题的一种方法[7]。
多目标优化问题一般由两个部分组成:1)若干目标函数;2)若干约束条件。
其数学模型可以描述如下式[7]:
式中:xd为决策向量;X=[x1,x2,…,xd,…xD]为决策向量形成的决定空间;n为优化目标总数;Fn(x)为第n个目标函数;F(x)为目标向量组成的目标空间;Gi(x)≤0为第i个约束不等式;Hj(x)=0为第j个约束等式;不等式Gi(x)≤0和等式Hj(x)=0确定了最优解的可行域,Xd_min和Xd_max为各维解向量搜索的上限和下限。
1.2 遗传算法含义及其原理
遗传算法是模拟生物遗传和进化过程的一种自适应收敛算法[8],其模拟自然进化论的优胜劣汰准则,用编码求解问题。在求解的过程中,一方面用最优个体进行迭代,另一方面遵循优化基因杂交的准则,变异最优个体的基因选择。相应基因在融合的过程会发生突变,这个过程中,利用适应度函数进行种群个体的评价分析,再经过选择、交叉、变异等方式进行组合,增加适应度较高个体的繁殖概率,使下一代适应度更高。随着不断迭代,求得最优解。遗传算法流程如图1所示[7]。

图1 遗传算法流程图
具体求解步骤如下:
1) 编码:将求解问题进行二进制编码转换。
2) 创建初始化群体:群体数过大会影响优化收敛速度,过小会降低种群多样性,应结合实际参数数量确定种群大小,一般取参数数量的5~10倍。
3) 适应度函数确定:通过需求解的最优化目标函数得到。
4) 选择、交叉、变异:通过最佳的优化策略,保留适应度最高的个体结构,保证优化后的历代为最优解;需要选取偏大一点的交叉概率,约在 0.45~0.90之间,既可保证新个体技能快速生成,又能保证不抑制进化算法;选取合适的变异率,抑制新个体早熟,范围选取在 0.002~0.150之间,保证新个体产生过程与优化算法的原则相符。
5) 终止条件:一般设定最大的进化代数或者种群的收敛度作为相应的终止条件。
2 电磁噪声产生机理研究
定转子之间的电磁力可分解为切向电磁力、径向电磁力。因谐波的存在,导致切向电磁力产生波动,形成转矩脉动进而引起电机相关部件抖动,由此产生振动噪声。因此,本节主要从转矩脉动的产生的机理来阐述降低转矩脉动的方法。
2.1 定子基波电流产生的转矩
2.1.1 定、转子主波磁场作用产生的转矩
当定子三相绕组通入对称正弦三相交流电流时,就会在气隙中产生一系列磁极对数不同的旋转磁势和磁场,其中与转子磁极对数p相同的称为主波磁场,转子主波磁场与定子主波磁场极数相同,转向和转速也相同,因此它们相互作用就会产生恒定的转矩,没有转矩脉动,这是永磁同步电机工作的基础,也是我们所需要的。
2.1.2 定、转子谐波次数相同的磁场作用产生转矩
定子通入基波电流时,除产生主波磁场外,还产生一系列的谐波磁场,这一系列谐波磁场可能包括分数次、偶数次、奇数次等。由于转子磁势不存在偶次谐波和分数次谐波,因此只有奇整数次的定子谐波磁场才有可能与转子谐波磁场极数相同,从而相互作用产生转矩。又因为定子谐波磁场的转速不是同步转速,而转子谐波磁场的转速却全部是同步转速,二者极数相同但转速不同,所以相互作用产生转矩脉动。如果把主波磁极对数p作为基波,并把它的转向定义为正转向,那么只有定子的-5,+7,-11,+13,-17,+19,…次谐波与转子的+5,+7,+11,+13,+17,+19,…次谐波相互作用产生转矩。
2.2 定子谐波电流产生的转矩
2.2.1 谐波电流产生的主波磁场与转子主波磁场相互作用产生的转矩
由于定子谐波电流产生的主波磁场转速为υn1(υ为电流谐波次数),而转子主波磁场转速为n1,二者极数相同转速不同,因此相互作用产生脉动转矩,脉动频率为6kf1,相对转频为6kp倍频(k=1,2,3,…)。
2.2.2 谐波电流产生的谐波磁场与转子谐波磁场相互作用产生的转矩
当电流的时间谐波次数与所产生的磁势空间谐波次数相同时(υ=λ),磁势的转速均为+n1,与转子λ次谐波磁场极数相同、转速相等、转向相同,因此二者相互作用产生恒定转矩。
当电流的时间谐波次数υ与所产生的磁势谐波次数λ不相等时(υ≠λ),该定子λ次谐波磁势的转速(计及转向)为(υ/λ)n1,与转子λ次谐波磁场极数相同,但转速不同,二者相互作用产生转矩脉动。二者的转速差为(1-υ/λ)n1,脉动频率为|λ-υ|f1,相对转频为|λ-υ|p倍频,由于υ和λ均可写作6k+1的形式,|λ-υ|即可写作6k的形式,因此上述转矩脉动频率为6kf1,相对转频为6kp倍频(k=1,2,3,…)。
通过以上分析可知,降低转矩脉动主要可以通过以下途径实现:
1)降低定转子5、7次,11、13次谐波含量,主要降低幅值较大的5、7次谐波;
2)降低谐波电流产生的与电机同步转速不同的5、7次谐波磁场。
3 多目标遗传算法数学模型建立
3.1 优化变量选择及优化区间确定
优化变量的选择对优化过程和优化结果有着重大影响,是电机优化设计问题求解的关键步骤。从理论上讲,电机的所有设计参数都可当作优化变量,但这种做法并不复合实际,一般情况下,优化变量的选择按照以下原则进行:
1) 优化变量的数量选取要适当,由于优化变量编码采用二进制,编码长度会随着优化变量数量呈现指数增长,数量过多会使计算量激增,但数量过少又会限制目标函数的变化,可能导致最后求得的结果只是局部最优解。
2) 优化变量应该取与目标函数相关性大的参数,比如磁钢长度(极弧系数)、定子槽口宽度、辅助槽的尺寸、位置等。
3) 确保各变量之间不互相干涉。
基于以上原则,优化变量选取如图2所示,其取值范围如表1所示。

图2 电机拓扑结构
表1 优化尺寸参数表

结构参数取值范围定子槽口宽度S1/mm3.2~3.6定子槽肩角度S2/(°)112~116磁钢槽长度R1/mm28~30磁钢槽厚度R2/mm2.8~3.0辅助槽位置角度R3/(°)13~17半圆辅助槽宽度R4/mm1.1~2.0
3.2 优化目标选取
优化目标的选择很大上程度取决于电机的种类及应用场合,本次优化主要关注电机的NVH噪声性能,故优化目标主要包括:
1) 电机转矩密度最大化。电机转矩密度是指电机外形尺寸不变条件下,单位电流产生的转矩。描述了单位电流电机的出力大小,与电机效率(所述效率对比皆为4000r/min额定点工况)基本等效。
2) 转矩脉动最小化。电机转矩脉动由各次空间次数相同但转速不同的谐波相互作用引起,且主要由定、转子产生的幅值较大的5、7次谐波引起,因此将转子5、7次谐波之和占基波比例最小作为优化目标,因其与转矩脉动等效,本文以转矩脉动进行描述。
3) 齿槽转矩最小化。齿槽转矩由定子开槽产生的齿谐波与转子谐波相互作用产生,与转矩脉动导致噪声产生的原理一致,也是我们需要关注的对象。
3.3 各优化目标特性之间的关系
本次仿真优化所用激励源采用理想正弦波电流源,电流有效值8.91A,频率50Hz。
通过基于遗传算法的多目标优化,可以得出不同目标之间的Pareto最优曲线,曲线上点即为相对最优解,以下分别分析仿真得出的输出转矩、转矩脉动、齿槽转矩之间的关系。
3.3.1 输出转矩-转矩脉动
在输出转矩与转矩脉动形成的Pareto曲线上,如图3所示,随着输出转矩增大,转矩脉动先减小后增大,转矩脉动存在最小值点。权衡两者与电机设计需求,取五星处对应点的方案作为优选方案。

图3 输出转矩-转矩脉动相关性
原方案与优化方案下的尺寸参数及特性对比如表2所示

表2 尺寸参数及特性对比表
3.3.2 齿槽转矩-转矩脉动
如下图4所示,在齿槽转矩与转矩脉动形成的Pareto曲线上,随齿槽转矩增大,转矩脉动先减小后增大,转矩脉动存在最小值点。综合考虑两者之间的关系,取五星处对应点的方案作为优选方案,其与原方案对比如表3所示。

图4 输出转矩-转矩脉动相关性

表3 尺寸参数及特性对比表
4 最优化方案选定及实验验证
4.1 最终优化方案确认
根据前文分析,由于电机扭转振动产生的噪声主要由转矩脉动引起,故优先考虑电机转矩脉动和输出转矩的性能,对齿槽转矩做校核即可。根据前文转矩脉动-输出转矩关系得出的优选方案对比加入齿槽转矩性能,如图5所示。显然齿槽转矩超出理想范围;当电机高转速运行时,某一转速下也易与结构产生谐振,故此方案非最优化方案,需在确保转矩脉动及输出转矩无明显恶化的前提下降低齿槽转矩。

图5 原方案与转矩脉动优化方案特性对比
综合齿槽转矩、转矩脉动、输出转矩性能进行方案选取,三种方案性能对比如图6所示,结构参数如表4所示。

图6 三种方案性能特性对比
表4 三种方案结构参数及特性对比表

优化项目原方案转矩脉动优选方案最终方案S1/mm3.23.53.4S2/(°)114115114R1/mm28.228.828.4R2/mm2.833R3/(°)151516R4/mm1.11.41.2
4.2 实验验证对比
4.2.1 电流波形测试
通过Tektronix MDO3054示波器检测电机实际运行时电流波形,验证实测与仿真电流波形的一致性,实测电流波形及其波形FFT分解如下图7所示。示波器显示电流有效值为9.157 A,对图7电流波形进行FFT分解,其总谐波畸变率仅为3.8%,故激励源可采用理想正弦波电流等效。

图7 实测电流波形及其FFT分解
4.2.2 噪声性能测试
按照优化后冲片结构参数试制样机,采用经专业第三方机构鉴定通过的噪声测试设备对电机三个额定负载点进行了噪声测试,将原方案与最终优化方案分别进行对比,测试结果如图8~图10所示。
Fc 工况:全噪声值由优化前67.9 dB(A)下降至66.5 dB(A)。

图8 Fc工况噪声优化前后对比
Fh 工况:全噪声值由优化前69.4 dB(A)下降至66.6 dB(A)。
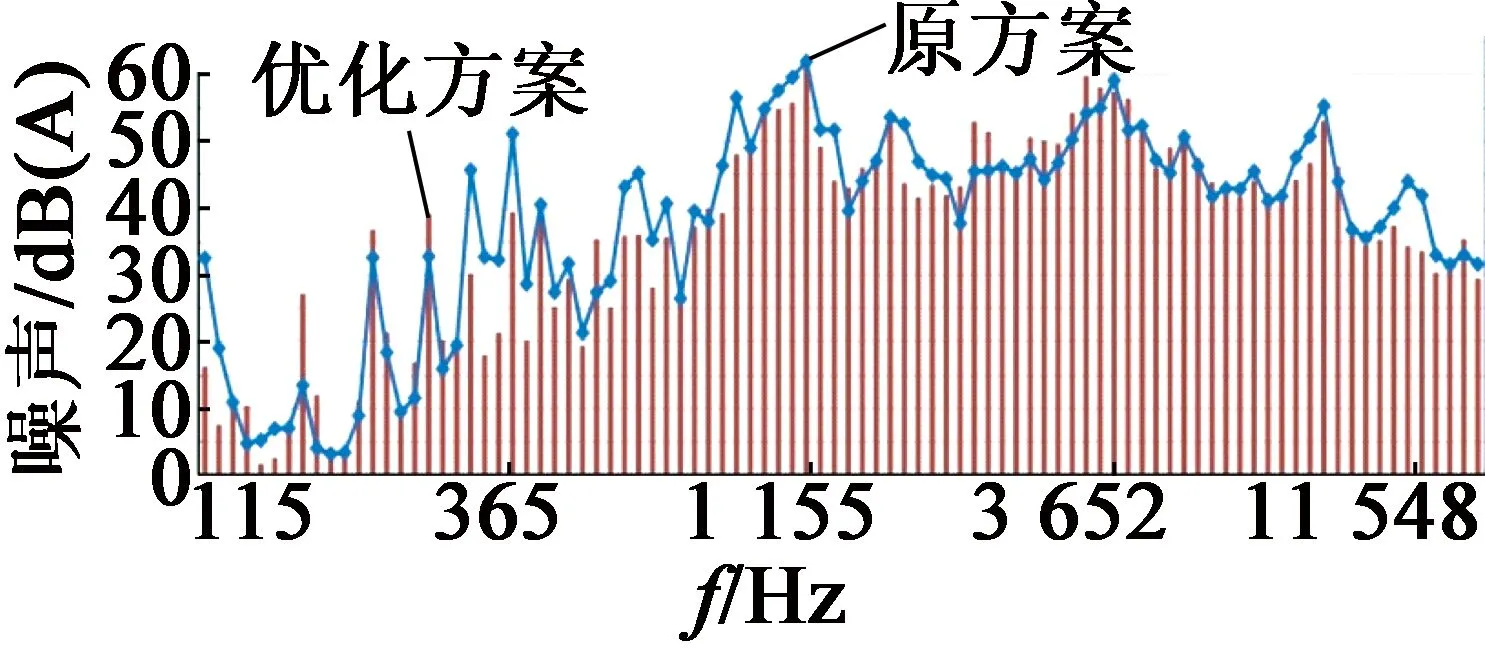
图9 Fh工况噪声优化前后对比
JIS 工况:全噪声值由优化前73.5 dB(A)下降至72.4 dB(A)。

图10 JIS工况噪声优化前后对比
4.2.3 效率测试
采用日立通用变频器控制额定点转速,以及配置有美国MAGTROL扭矩传感器的全自动磁滞测功机(图11)进行效率检测。效率测试结果如图12所示,在1 000~5 000 r/min转速范围内,优化后方案与原方案相比均有1%~2%的效率提升。

图11 磁滞测功机

图12 效率测试对比
5 结 语
本文以输出转矩最大、转矩脉动最小、齿槽转矩最小为优化目标,基于多目标的遗传优化算法,对电机的冲片结构进行了定向优化,得出以下结论:
1) 遗传算法可以大大提升计算效率,与普通遍历式参数化优化相比,其加快了最优解收敛速度,且通过实验验证了此种方法的有效性;
2) 各个优化目标有时并非正相关,需要权衡电机设计需求与设计目标之间的关系,以获得电机的最佳设计;
3)采用遗传算法能减少计算的工作量,多目标同时优化,可以实现不同设计指标的权衡,根据电机种类以及实际工作需求选取不同的指标进行设计。

