短期风速数据极值分布研究

王 勃，臧永志，董丽欣

1吉林建筑大学 土木工程学院,长春 130118 2吉林省结构与抗震科技创新中心,长春 130118

0 引言

近年来，随着我国经济发展和城市化进程的推进,新兴城市高层、高耸房屋建筑日益增加,风荷载作为此类工程结构设计的重要荷载,在结构设计计算中起着至关重要的作用.研究发现风灾是自然灾害中最大的灾害之一,全球每年因风灾造成的经济损失达到百亿美元[1].风荷载的取值过高会导致资源的浪费,过低就有可能遇到风险导致结构破坏,因此需要确定合理的风荷载取值[2-3].正确的计算和确定不同重现期的基本风压,对于建筑结构抗风设计和资源合理利用都具有重要的理论价值和现实意义.

样本选取、模型选取和参数估计是运用数理统计方法计算最大风速的3个步骤[4].《建筑结构荷载规范》[5](以下简称《规范》)中选取年最大风速资料,运用极值Ⅰ型分布进行研究,一般应有25年以上的风速资料,当样本容量无法满足时也至少应该有10年的风速资料.一些新兴城市无法提供长期风速资料样本,当采用5年以下的风速资料作为样本统计时,为避免样本容量的不足,采用月最大风速资料作为样本点符合极值分布.《规范》中模型选取时年最大风速资料最初被认为服从极值Ⅱ型[6]分布,后来随着研究的深入,学者们发现极值Ⅰ型拟合风速资料更好[7-8];也有学者认为风速资料统计选用极值Ⅲ型更为合适[9],国外也有规范选取极值Ⅲ型分布拟合风速资料.参数估计选用拟合标准差和拟合相对偏差,用柯尔莫哥洛夫检验法进行检验.用符合检验的月最大风速代入极值Ⅲ型分布得出重现期为10年、50年和100年的基本风压值,与规范中的基本风压进行比较分析.

1 基本风压的计算

1.1 样本选取

风速数据资料来自环境气象数据中心,数据集全名为中国地面国际交换站气候资料日值数据库,本文从中选取黑龙江省28个主要城市2014年-2018年的风速数据资料进行拟合计算分析,风速资料的时距是定时4次2 min平均风速,《规范》[5]中规定风速资料应取自记风速仪的10 min平均风速资料,对于非自记的风速观测资料需要进行修正,修正应考虑风速资料的均一性,对不均一的数据结合周围气象站资料加以修正,其换算关系如下:

y=ax+b

(1)

式中,y为自记10 min平均风速,m/s;x为4次定时2 min平均风速,m/s;a为系数,对东北地区a=0.97;b为系数,对东北地区b=3.94 m/s.

基本风压的计算公式为:

(2)

式中,w0为基本风压,10-3kN/m2;ρ为空气密度,kg/m3;v0为最大风速,m/s.

1.2 极值Ⅲ型分布及其参数估计

极值Ⅲ型分布函数表达式:

(3)

其分布密度函数表达式:

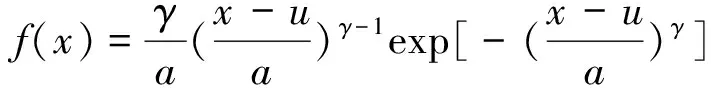
(4)

重现期为R时的最大风速表达式:

(5)

式中,x为风速资料中的样本值,m/s;a为尺度参数(a>0);u为位置参数,m;γ为形状参数(γ>0);计算参数a,u和γ采用参数估计法、有变量替换法和最小二乘法[10].

1.2.1 变量替换法

变量替换法计算起来比较简便,得到的参数估计值有效性较高[11].

先令：

(6)

则变量y的密度函数[12]为:

f(y)=γexp[γy-exp(γy)]

(7)

用Γ函数[10]计算y的数学期望E(y)和方差σ2(y)：

(8)

(9)

欧拉常数c为0.577 22.由式(8)和式(9)可得:

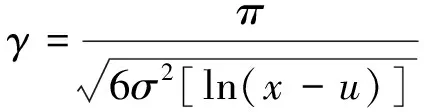
(10)

(11)

取

u=xmin-ε(ε>0)

(12)

式中,xmin为风速数据中最小值,m/s;调整ε值可得到不同的u,将u代入ln(x-u)的数学期望和方差：

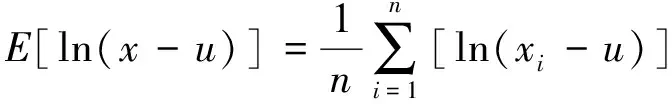
(13)

(14)

将得到的数学期望和方差代入式(10)和式(11)可得到一系列与u值对应的a和γ,根据参数估计优良性的指标,选择最优的一组作为参数估计值.

1.2.2 最小二乘法

选用最小二乘法进行参数估计时,首先应把分布函数转换成Y=BX+A的线性函数,然后根据偏差平方和最小的原则求出参数A,B.由式(3)极值Ⅲ型线性变换式:

ln{-ln[1-F(x)]}=γln(x-u)-γlna

(15)

式中,Y为ln{-ln[1-F(x)]}；B为γ；X为ln(x-u)；A为-γlna.将风速统计数据中的样本x值由小到大顺序排列,得到F(xi)=i/(n+1),然后根据文献[10]确定A和B表达式:

(16)

(17)

由式(12)确定u值,代入式(16)和式(17)得出a和γ,调整ε值可得到很多组u，a和γ,将拟合最好的一组值作为参考值.

1.3 计算结果优良性检验指标

每一组参数都有不同的参数估计方法,参数估计方法在于衡量计算结果的优劣性.分别用拟合标准差、拟合相对偏差和柯尔莫哥洛夫拟合适度作为衡量计算结果的优良性指标[13].

1.3.1 拟合标准差

拟合标准差定义式如下:

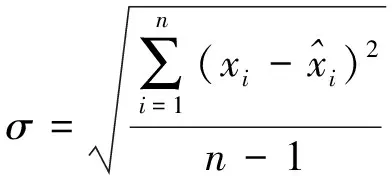
(18)

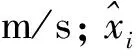
对极值Ⅲ型分布:

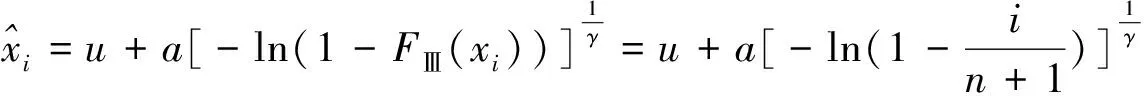
(19)

1.3.2 拟合相对偏差

拟合相对偏差定义式如下:

(20)

1.3.3 柯尔莫哥洛夫拟合适度

柯尔莫哥洛夫拟合适度定义式如下:

Dn=max{[Fn*(x)-F(x)]}

(21)

式中,Dn为理论分布与经验分布的最大偏差;F(x)和Fn*(x)分别为理论分布函数和经验分布函数;由文献[10]给出F(x)和Fn*(x)计算方法.

由柯尔莫哥洛夫准则可以得到柯尔莫哥洛夫拟合适度检验指标:

(22)

式中,n为样本容量,用柯尔莫哥洛夫检验法进行检验,取信度α为5 %,查表可得Kα=1.35,当Kf<1.35时,则认为样本服从极值分布；反之,则不服从.

2 计算结果与分析

利用黑龙江省28个城市在2014年-2018年月最大风速资料,运用极值Ⅲ型分布进行统计分析,选用变量替换法和最小二乘法对其参数进行计算.得出极值分布参数a，u，γ及优良性检验指标σ，V，Dn,如表1所示.

表1 极值Ⅲ型分布参数估计优良性检验计算结果Table 1 Goodness test calculation results of extreme value type Ⅲ distribution parameter estimation

续表1

续表1

通过比较参数估计优良性指标值来选择极值Ⅲ型分布最优的参数估计方法.首先看柯尔莫哥洛夫拟合适度Dn,如果Dn<0.174 3(Kf<1.35),表明该城市月最大风速资料服从极值Ⅲ型分布.此外,拟合标准差σ在检验指标中精度最高,在比较分布参数优劣性时,先以参数σ为指标(σ越小表明精度最高),若σ相同时,再比较V值.

由表1可以看出,黑龙江省28个城市月最大风速资料都符合极值Ⅲ型分布,由于22个城市以变量替换法为优,6个城市以最小二乘法为优.对月最大风速资料拟合分析时,选用极值Ⅲ型分布采用变量替换法更优.

选用极值Ⅲ型分布变量替换法计算基本风压,当重现期为T年时,选用月最大风速资料时,将R=12T带入式(5).计算出黑龙江省28个城市重现期为10年、50年和100年的基本风压,将结果与规范中基本风压值进行相较分析,见表2.

表2 基本风压结果比较Table 2 Comparison of basic wind pressure results

续表2

选用5年月最大风速资料运用极值Ⅲ型分布计算基本风压与规范给出基本风压相比较,重现期为10年时,计算值大于规范值的城市有呼玛、北安、伊春、泰来和宝清5个城市,占总城市18 %,相差最大城市为宝清,其计算值比规范值大0.131 kN/m2.总体来说，大部分城市的计算值小于规范值,平均相差0.008 kN/m2.重现期为50年时,计算值大于规范值的城市只有宝清,其余城市的计算值均小于规范值,平均相差0.098 kN/m2.重现期为100年时,计算值大于规范值的城市只有宝清,其余城市的计算值均小于规范值,平均相差0.144 kN/m2.结果表明，短期风速资料下的基本风压与规范值基本吻合,大部分城市规范值大于计算值,表明规范给出基本风压相对安全保守.在只有短期风速资料条件下,使用月最大风速资料计算重现期10年以下比如拆除结构的基本风压不失为一种可行方法.

3 结论

通过对黑龙江省28个城市五年月最大风速资料进行统计分析,计算出重现期为10年、50年和100年的基本风压,得出以下结论:

(1) 基于短期风速资料，黑龙江省28个城市月最大风速资料符合极值Ⅲ型分布,对于极值Ⅲ型分布,变量替换参数估计法优于最小二乘法.

(2) 黑龙江省28个城市在短期风速资料下基本风压的计算值与规范值相差不大,在黑龙江省一些新兴城市在没有长期风速资料下,采用月最大风速资料拟合极值Ⅲ型分布计算重现期10年以下拆除工程的基本风压可以作为参考使用.

规范中未给出重现期10年以下的基本风压值,短期风速资料下月最大风速服从极值Ⅲ型分布.对于没有长期风速资料的地区,如一些新兴城市或规范中没有给出基本风压的地区,出于对安全性和经济性的综合考量,可采用这种方法计算重现期较短如拆除结构的基本风压.