永磁同步电机无磁链电流预测控制
吴嘉欣,张 懿,魏海峰,田会峰,丁桃宝
(1.江苏科技大学 电子信息学院,镇江 212003;2. 苏州晋宇达实业股份有限公司,张家港 215000)
0 引 言
永磁同步电机具有结构简单、功率密度高、运行可靠等优点,但在其运行过程中,电机定子电感、转子磁链以及负载转矩实时变化,常规的PI控制技术已无法满足工业自动化对系统鲁棒性的要求[1]。近年来,学者们研究各类非线性控制方法,如滑模变结构控制[2]、反馈线性化控制[3]、自抗扰控制[4]、反步控制[5]以及PWM预测控制[6]等。
滑模变结构控制因其对内部参数不确定性和外部干扰不敏感的优点被广泛应用,其在设计过程中只需考虑不确定性边界选择,便可保证系统鲁棒性[7]。然而,为保证系统Lyapunov稳定性,不确定性边界通常需选择得比实际边界大,从而容易引起系统抖振。反馈线性化控制是近20年来研究的热点,通过适当的坐标变换,可以将原非线性模型转化为线性模型。但是,由于该方法需以精确的系统非线性数学模型为基础,当考虑参数不确定性和未知干扰时,该方法无法适用。自抗扰控制通过扩张状态观测器观测并补偿系统内外扰动[8]。然而,采用扩张状态观测器的控制系统仍会受参数不确定性的影响。反步控制为20世纪90年代初提出的以Lyapunov稳定性理论为基础的控制方法,其因易与自适应参数估计技术结合以减小系统内外扰动的影响而受到重视。该方法通过引入虚拟控制变量,将原始高阶系统分解为串级子系统,逐一对其构造合适的Lyapunov函数并推导虚拟控制律,保证系统渐近收敛,最终导出实际的控制律及自适应律[9]。PWM预测控制将经典PI控制结构与空间矢量脉宽调制相结合,基于永磁同步电机模型的离散方程,计算并应用下一采样时间的电压矢量,电机的内部参数如定子电阻、电感以及转子磁链随运行过程中温度的变化而变化,该参数摄动会引起预测控制中给定电压空间矢量的变化[10],影响电流控制的性能,有效的扰动观测和参数辨识对于电流预测控制的鲁棒性是必要的,但扰动观测和参数辨识极大增加了算法的复杂性。
综上分析,相对于传统永磁同步电机PWM电流预测控制,滑模变结构控制在抗电机内部参数摄动的鲁棒性方面具有一定的优势。然而,为保证系统Lyapunov稳定性,较大的控制增益选取容易引发系统抖振,影响电机系统的运行性能,而PWM电流预测控制并无该缺点。针对传统永磁同步电机PWM电流预测控制对电机模型参数的依赖性问题,研究基于增量式模型的永磁同步电机无磁链电流预测控制方法。首先,对传统PWM电流预测控制的稳定性以及参数摄动造成的电流静差进行了理论分析,分析表明参数摄动会对系统稳定性造成影响,造成电流静差。其次,建立基于增量式状态方程的永磁同步电机模型,基于此模型设计无磁链电流预测控制器,保证算法能够在无需磁链参数参与的情况下运行,增强系统对磁链参数摄动的鲁棒性。
1 传统PWM电流预测控制
永磁同步电机在d,q轴下的数学模型:
(1)
式中:ud,uq为d,q轴电压;id,iq为d,q轴电流;R为定子电阻;Ld,Lq为d,q轴电感;ωe为电机速度;ψf为磁链。
考虑到系统电流环采样周期T极小,对式(1)左边进行一阶泰勒展开,得到:
(2)
将式(2)代入式(1)中,得到离散电压状态方程:
x(k+1)=A(k)x(k)+Bu(k)+d(k)
(3)

假设xref(k+1)为电流给定值,将式(3)中的x(k+1)替换为xref(k+1),则通过PWM电流预测控制得到的电压指令:
u(k)=B-1[xref(k+1)-A(k)x(k)-d(k)]
(4)
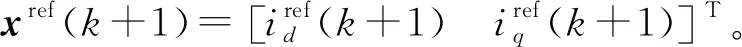
式(3)A(k)矩阵中1-TR/L项近似为1,设PWM预测控制中所用电感和磁链参数为L和ψf,对应实际电机参数为L0和ψf0,则永磁同步电机离散状态方程另可表示:
x(k+1)=A(k)x(k)+B0u(k)+d0(k)
(5)

将式(4)代入式(5),得到PWM预测控制中存在参数摄动时的电流关系:
(6)
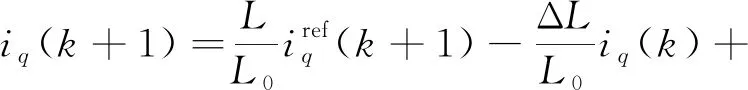
(7)
式中:Δψf=ψf-ψf0,即转子磁链参数摄动量;ΔL=L-L0,即定子电感参设摄动量。
对式(6)和式(7)进行z变换,得到:
(8)
根据式(8)可知,为了保证闭环系统的稳定性,传统PWM预测控制器中电感L和电机实际电感L0需满足如下条件:
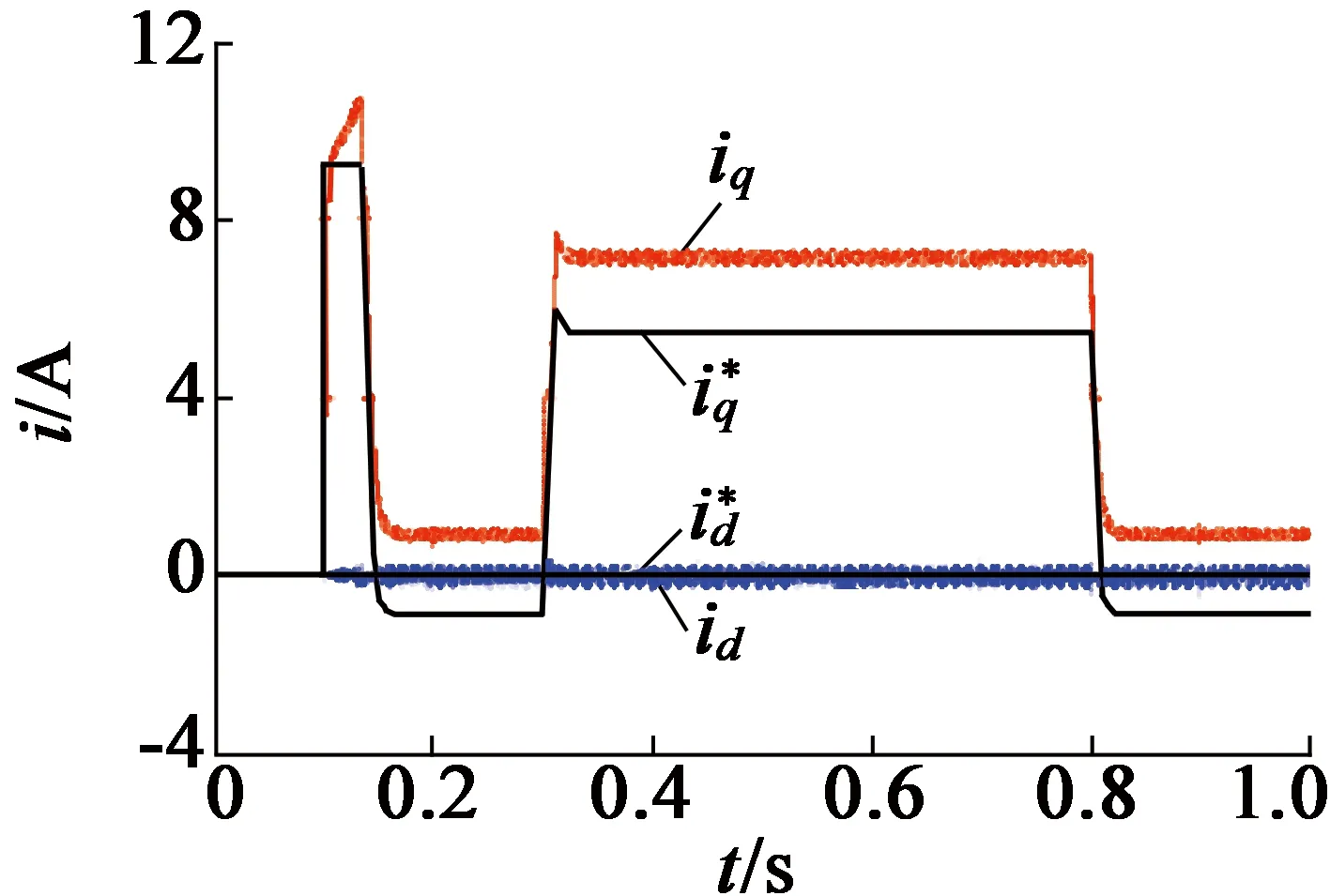
0 (9) 在两个相邻的电流环控制周期内,可以认为: (10) 将式(10)代入式(6)与式(7)中,得到: (11) (12) 从式(11)与式(12)中可以看出,当控制器中的参数(转子磁链和定子电感)存在摄动时,会造成指令电流与实际电流之间的静差。 永磁同步电机状态方程: Δx(k+1)=A(k)Δx(k)+BΔu(k)+Δd(k) (13) 当转子电角速度ωe保持不变时,d(k)的增量可以表示: (14) 对于线性系统,状态方程等价于增量式状态方程,即: (15) 电流环给定控制电压指令: Δu(k+p)=Δu(k+p-1)=Δu(k+1)=0 (16) 式中:预测域p=2。 在采用多步预测后,状态方程改写: Yk=SuΔu(k)+SxΔx(k)+Ex(k) (17) 选取评价函数: J=(Yk-Iref)TQ(Yk-Iref) (18) 式(18)中引入中间变量ρ=(Yk-Iref)4×1可得到: J[x(k),Δx(k),Δu(k)]=ρTQρ (19) 将式(17)代入中间变量ρ,ρ表达式: GΔu(k)-H(x) (20) 评价函数J的极值条件: ⟹Δu(k)=(GTQG)-1GTQH(k) (21) J关于Δu(k)的二阶偏导数: (22) 二阶偏导数正定,则式(21)表示的Δu(k)为最优电压增量。根据式(20),Δu(k)可表示: (23) 式中:H(k)=Iref-SxΔx(k)-Ex(k)。 在k时刻,PWM预测控制得到的电压指令为上一时刻的电压指令与本时刻计算出的最优电压增量之和,即: u(k)=u(k-1)+Δu(k) (24) Δx(k+1)=AΔx(k)+BΔu(k)= (A-BKpcSx)Δx(k)-BKpcEx(k)+BKpcIref (25) 考虑到x(k)=x(k-1)+Δx(k),将式(25)中不包含Δx(k)的其他项之和记为δ,则式(25)可表达: Δx(k+1)=AΔx(k)+BΔu(k)= (A-BKpcSx-BKpcE)Δx(k)+δ=MΔx(k)+δ (26) 当控制器中电感参数无摄动时,M矩阵: (27) 将式(23)变化: Δu(k)=[BTQB]-1BTQ[I*(k+1)-AΔx(k)-x(k)] (28) 根据矩阵变换理论可知: [BTQB]-1BTQ=B-1 (29) 将式(29)代入式(28)中,得到: Δu(k)=B-1[I*(k+1)-AΔx(k)-x(k)] (30) 将上式代入式(15)中,得到: Δx(k+1)=AΔx(k)+BΔu(k)= AΔx(k)+BB-1[I*(k+1)-AΔx(k)-x(k)]= I*(k+1)-x(k) (31) 由于Δx(k+1)=x(k+1)-x(k),由式(31)可以得到: I*(k+1)=x(k+1) (32) 对无磁链电流预测控制进行实验研究,实验平台如图1所示。 图1 实验平台 实验电机参数:额定功率1.2 kW,额定电压220 V,额定电流6.5A,额定转矩4.6N·m,额定转速2 500 r/min,定子电阻0.55 Ω,d,q轴电感4.34 mH,电机极对数为4。 为更为直观地体现新型无磁链电流预测控制策略在抗磁链参数摄动方面的优势,实验将其与传统PWM电流预测控制进行对比,控制器分别给定2倍和0.5倍的实际磁链值。 图2为传统PWM电流预测控制下的电流实验波形,图2(a)为控制器给定2倍实际磁链,图2(b)为控制给定0.5倍实际磁链。电机在0.1 s时刻空载起动,0.3 s时刻给定电机突加额定负载,0.8 s时刻突卸负载。由图2可知,控制器给定2倍实际磁链时,无论空载工况还是额定负载工况,电机直轴电流严格跟随给定电流,始终在0上下浮动,交轴转矩电流始终高于给定值1.9 A左右,电流控制静差明显;同样,控制器给定0.5倍实际磁链时,无论空载工况还是额定负载工况,电机直轴电流严格跟随给定电流,始终在0上下浮动,而交轴实际转矩电流始终低于给定值1 A,电流控制静差同样明显,由此验证传统PWM电流预测控制对于转子磁链参数摄动鲁棒性不佳。 (a) 2倍实际磁链 (b) 0.5倍实际磁链 图3为新型无磁链电流预测控制下的电流实验波形,图3(a)为控制器给定2倍实际磁链,图3(b)为控制给定0.5倍实际磁链。同样,电机在0.1 s时刻空载起动,0.3 s时刻给定电机突加额定负载,0.8 s时刻突卸负载。对比图2可知,控制器无论给定2倍实际磁链还是0.5倍实际磁链,交直轴电流实际值均始终严格跟随跟定值,电流控制几乎无静差,由此验证新型无磁链电流预测控制对于转子磁链参数摄动的强鲁棒性。 (a) 2倍实际磁链 (b) 0.5倍实际磁链 本文研究了一种基于增量式模型的永磁同步电机无磁链电流预测控制方法。对传统PWM电流预测控制的稳定性进行了分析,基于增量式模型设计无磁链电流预测控制器,保证算法能够在无需磁链参数参与的情况下运行,增强系统对磁链参数摄动的鲁棒性。为更为直观地体现新型无磁链电流预测控制策略在抗磁链参数摄动方面的优势,选取1.2 kW永磁同步电机为实验对象,实验将无磁链电流预测控制与传统PWM电流预测控制进行对比,结果验证了无磁链预测控制对于磁链参数摄动有着较强的鲁棒性。2 增量式模型建立
3 基于增量式模型的无磁链预测控制


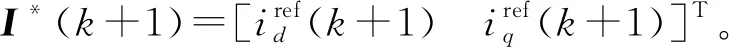
4 实验结果及其分析




5 结 语

