车用爪极发电机电磁振动影响因素研究

李志波，杨 依，王映品，3，陈昌平，李功捷，钟承尧

(1.海南师范大学 物理与电子工程学院，海口 571158；2.一汽海马汽车有限公司，海口 570216；3.海南省激光技术与光电功能材料重点实验室，海口 571158)

0 引 言

车载爪极交流发电机噪声通常包含机械噪声、空气噪声和电磁噪声[1]；机械噪声和空气噪声通过学者和工程师的努力研究，已能较好应对。爪极交流发电机电磁噪声由于涉及到电磁力学、结构力学、声学和材料特性，传播路径复杂，未能进行充分研究，特别是整车主机厂往往难于应付。

近年来，已有部分高校和企业联合对车载发电机电磁噪声进行了部分研究。Mohamed S等利用数值仿真方法计算电动机定子每齿段的电磁力；将电磁力耦合到结构，计算出结构振动；用结构振动计算出辐射噪声；最后进行部分降噪优化研究[2]。吴双龙等提出了一种新的数值仿真计算方法来计算爪极式交流发电机的电磁振动和噪声[3]。韩伟等用有限元法计算了定子的振动模态和固有频率，最后与实验结果进行比较，计算结果和实验结果符合性较好[4]。赵汝炫等建立了车用交流发电机仿真模型，计算出电磁力，与结构耦合，计算出结构振动情况，再通过结构振动计算出辐射噪声，与实际测试结果吻合度较高，但没有对电磁噪声的影响因素进行研究[5]。闫荣格等研究了定子磁致伸缩效应对感应电机振动影响[6]。张冉等研究了偏心气隙距离与电磁力波径向振幅的关系，指出设计合适的偏心磁极，可以有效地改善电磁振动和噪声[7]。唐贵基等人分析了径向气隙偏心对汽轮发电机转子径向不平衡磁拉力及其振动特性的影响[8]。左曙光等研究了转子结构，特别是爪极形状对电磁噪声的影响[9]。在以上理论研究的同时，部分学者也进行了相应的实验研究工作。吴双龙等对电机噪声的声源进行了识别与分析，系统地梳理了发电机各种噪声与电机结构的关系，针对电磁噪声部分得出其谐波频率是6kf(k=1，2，3，…)，f为电机转速基本频率，实测得出36阶电磁噪声贡献量较高，未进行电磁噪声影响因素分析[10]。刘星等通过改变电机负载大小，实验得到负载对电磁噪声的影响规律[11]。Andrea C等得出定子齿槽转矩振动是电机噪声主要因素的结论，并设计了1种电机冷却模型和2种永磁体形状进行噪声测试验证，以比较评估电机重新设计的潜在优点，通过测试验证了新的设计可以降低噪声，但是电机性能存在不可忽视的下降[12]。符为榕等在定子与机壳之间增加阻尼材料，降低了电机本体的36阶振动[13-15]。

综上，对电机电磁振动噪声主要从电机径向力、电磁力、定子磁致伸缩、定子固有频率等方向来进行研究。在电磁力方向主要根据麦克斯韦方程组进行数值分析，对影响因素研究较少，针对电机实际安装下进行的实验验证更少。本文推导出电磁力解析模型；分析4种因素对电磁力幅值的影响规律；装配相应参数电机进行实验验证；得出这些因素对电机机体电磁振动的影响规律，对降低电机电磁噪声有一定的指导意义。

1 电磁力解析模型

电磁振动是由于在定、转子气隙空间内交换的磁场产生的一个空间旋转力波，该力波使得定子和转子发生振动变形，振动传递到电机壳体上，从而辐射出的噪声。它与电机气隙内的谐波磁场以及由此产生的电磁力波幅值、频率和级数，以及定子本身的振动特性，如固有频率、阻尼、机械阻抗、定子与壳体的连接方式均有密切关系[1]。

电磁振动是在电磁力激励下的电机结构振动产生，因此可以通过电磁力的阶次来判断电磁振动的阶次，用电磁力的模型来分析引起电磁振动幅值的影响因素。当分界面上无电流片时，根据麦克斯韦应力张量法[13]可以得到单位面积张力的大小：

(1)

式中：Br是气隙中径向磁感应强度；Bt是切向磁感应强度，由于切向磁感应强度远小于径向磁感应强度，在此省略；μ0是真空磁导率。

由电机学中的磁路欧姆定律可知：

(2)

式中：Φ是磁通；S是垂直于磁感应强度的面积；F1是气隙磁动势；Λ是气隙磁路磁导。

假设磁路中导磁材料的磁阻远小于气隙磁阻，磁动势主要消耗在气隙上，得：

F=N1i1±N2i2≈F1

(3)

式中：F是磁路磁动势；i1，i2是转子线圈和定子线圈电流；N1,N2是转子线圈和定子线圈的匝数。将转子线圈和定子线圈电流用傅里叶级数展开，得到：

(4)

(5)

将式(4)，式(5)代入式(3)得到：

(6)

式中：Aν是定子磁动势第ν次谐波幅值；Αμ是转子磁动势第μ次谐波幅值；p为电机极对数；ωm为机械角速度；t为时间；α为空间机械角度。

由于气隙磁导是时间和空间的函数，其空间分量不影响时间分量的频率，故只考虑时间分量部分[10]。气隙磁导用傅里叶级数展开(忽略高阶分量)，得以下公式：

(7)

式中：Ak是气隙磁导第k次谐波幅值。

将式(2)、式(6)、式(7)代入式(1)，推导出：

cos[(k1+k2)±2pωmt-(k1±ν1+k2∓ν2)pα]+

cos[(k1±μ1+k2±μ2)pωmt-(k1±μ1+k2∓μ2)pα]+

sin[(k1±1-k2∓μ)pωmt-(k1±ν-k2∓μ)pα]}}

(8)

由式(8)可知，爪极发电机的电磁力是时间和空间的函数，电磁力频率只与时间项有关，推导出爪极发电机的径向电磁力频率：

f=(k1±k2±μ)pfr

(9)

式中：k1，k2，μ都取正整数；fr是电机旋转频率;p为极对数,p=6，因此电磁力频率为电机转速频率的6k倍。

2 各种因素对电磁振动幅值影响分析

2.1 电机负载对电磁力幅值的影响

由式(8)可知，电磁力的幅值受到定子磁动势幅值Aν影响，Aν越低，电磁力幅值越低。

由式(4)、式(5)、式(6)可知，Aν与电机定子线圈绕组匝数和流过线圈的电流成比例关系。电机线圈匝数通常是固定不变的，降低电机负载即相当于降低定子电流幅值Iν，进而降低Aν，因此可以通过降低电机负载来减小电磁力幅值。

2.2 定转子偏心距对电磁力幅值的影响

由式(8)可知，电磁力幅值受到气隙磁导幅值Ak的影响，Ak越低，电磁力幅值越低。如图1所示，考虑电机定子和转子的偏心距为δ。

图1 发电机气隙偏心

由图1可知，不同转角处的偏心距g(θ,t)≈g[1+δcos(ωt)]，因此，气隙磁导：

(10)

式中：g是转子与定子间的气隙平均距离；C是非气隙偏心参数外的影响因素。由式(10)可知，减少δ，气隙磁导减小。由式(7)可知，气隙磁导减小，气隙磁导第k次谐波幅值Ak减小，电磁力幅值减小。

2.3 爪极形状对电磁力幅值的影响

由式(8)可知，电磁力幅值受到转子磁动势幅值Aμ的影响，Aμ越低，电磁力幅值越低。

由式(6)可知，电机的转子磁动势Fr：

(11)

一对爪极表面励磁磁动势的空间分布如图2所示。

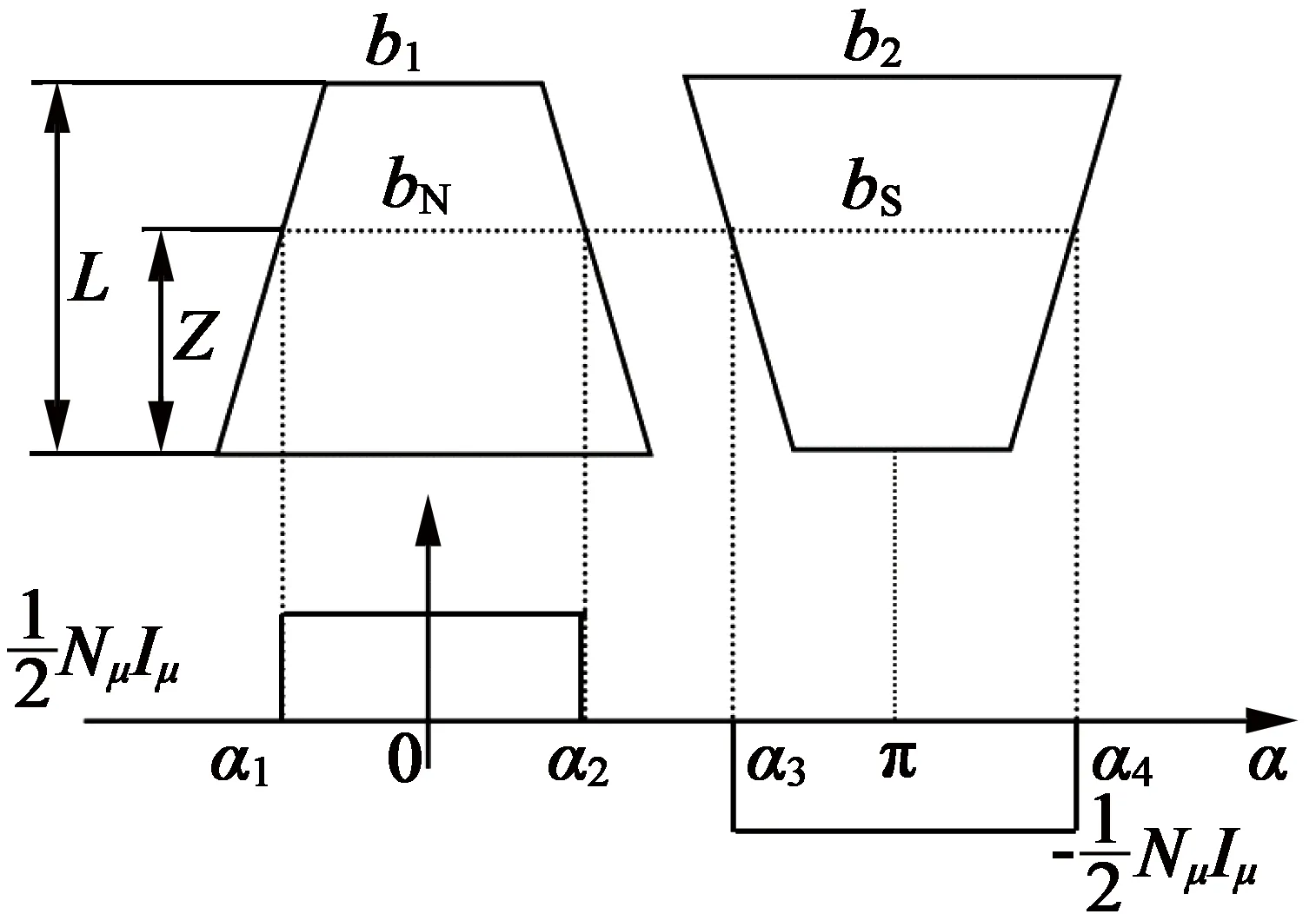
图2 转子磁动势

由图2中的几何关系可以得到：

(12)

(13)

将转子磁动势按照傅里叶级数展开,得到：

(14)

由式(11)～式(14)可知，改变爪极的极尖尺寸b1和极根尺寸b2能够影响Aμ。极根尺寸保持不变，bN-bS的值随着极尖宽度的增加而减小。

现有爪极形状极尖宽为7.0 mm，极根宽为29.2mm，将极尖尺寸从7.0mm增大到7.7mm，bN-bS的值由8.8降低到8.52，使得转子磁动势幅值Aμ减小，进而可以降低电磁力幅值。

3 爪极发电机机体电磁振动测试

3.1 爪极发电机

本文研究的是搭载在某1.5 T发动机上的JFZ1A33三相电机，其基本结构如图3所示。

图3 爪极发电机结构图

该电机主要由爪极转子、定子、前后端盖、前后冷却风扇、电力变换模块、机体和皮带轮组成。其中转子通过轴承支撑在前后端盖上，壳体和前后端盖都有通风口。该型号发电机定子有36个槽，用于安放电枢绕组，转子有6对爪极，前风扇11个叶片，后风扇有11个叶片。

电路原理图如图4所示。采用三相桥式全控整流电路，该电路输出电压一周期脉动6次，每次脉动的波形都一样，是6 脉冲波整流电路。

图4 爪极发电机电路图

3.2 实验

本次研究装配了5台样机进行测试。样机零部件相关尺寸性能参数经过挑选测试后组装，样机基本情况如表1所示。爪极形状A极尖宽7.0 mm，极根宽29.2 mm；爪极形状B的极尖宽度较形状A增加了8%，极尖与极跟之间的形状采用线性过渡。

表1 5台样机基本信息

测试图片如图5所示。在发电机机壳上安装Kistler的加速度传感器，采用朗德24通道采集设备，数据分析使用Artemis。

图5 发电机振动测试台架

测试工况选取了发动机怠速工况下电机的电磁噪声振动情况。发动机怠速转速(750±50) r/min；发电机到发动机转速传动比为2.55，因此发电机转速选择在1 900～2 000 r/min之间。测试过程如下：

1) 安装1#电机，空载和满载下测试，测试过程中记录转速，振动信号；

2) 改变负载量程分别为满量程、80%量程、60%量程、40%量程,进行测试；

3) 更换不同同轴度的2#、3#电机进行测试；

4) 更换不同转子动平衡的4#电机进行测试；

5) 更换不同爪极形状的5#电机进行测试。

4 影响因素测试验证

4.1 空载与满载下电磁噪声的确认

图6是电机满载和空载时电机机体的振动情况。控制1#电机转速为1 950 r/min、满载进行测试，电机本体径向振动加速度曲线在391 Hz，7 821 Hz，172 Hz处存在明显振动峰值。电机转速1 950 r/min，对应着转子基本频率为32.5Hz的12阶，24阶和36阶，其中36阶振动加速度值明显偏高。控制其负载为空载，测试结果显示各振动峰值消失。通过式(9)和图6测试结果可以证明，满载时振动加速度曲线的峰值就是电磁力导致的电机本体电磁振动。

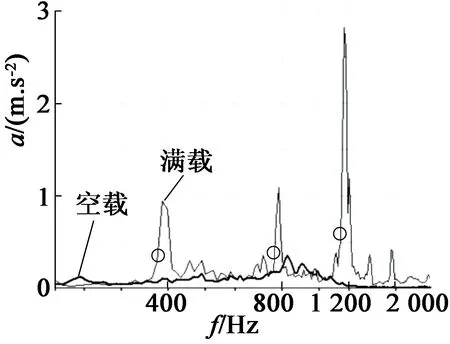
图6 1#电机满载和空载时本体振动加速度

4.2 电机负载对电磁振动影响

改变电机负载，测试电机本体的振动情况如图7所示。电磁力波引起的机体振动在36阶频率处随着负载的减小而减小，电机负载从满量程降低到40%量程时，产生的36阶电磁振动幅值从2.78 m/s2降低到1.5 m/s2。根据车辆用电量信息，在考虑安全余量的情况下进行负载优化能够有效降低电磁振动。控制负载输出，相当于减小磁动势的幅值，即减小式(8)的幅值Aμ和Aν来减少电磁力的幅值，降低电机机体电磁振动。

图7 1#电机不同负载下机体振动加速度

4.3 定、转子同轴度对电磁振动影响

图8是不同定、转子同轴度电机机体振动情况。从图8可以看出，随着同轴度的减小，36阶电磁力波引起的振动有明显的下降。同轴度从0.25 mm降低到0.18 mm，振动加速度从7 m/s2下降到2.8 m/s2；同轴度下降到0.11 mm，振动加速度下降1.6 m/s2。可见，同轴度在0.11～0.25 mm变化范围内，定、转子同轴度对发电机36阶电磁振动幅值有明显影响。减小定、转子同轴度，即减小定子与转子间的偏心距，可减小气隙磁导的幅值Ak，进而减小电磁力幅值，降低电机机体电磁振动。

图8 不同定、转子同轴度下机体振动加速度

4.4 转子动平衡对电磁振动影响

图9是不同转子动平衡电机机体振动情况。可见，转子前、后动平衡从1#电机的16.8 g·mm、13.7 g·mm变化到4#电机的7.8 g·mm、8.7 g·mm，在12阶处振动加速度有明显减小，但是在36阶振动加速度有增加。可能有两个方面原因导致这样的结果：一是不平衡量沿转子轴向的分布是不确定的，4#电机转子的不平衡质量在36阶振型的波腹位置，机械激励力与电磁激励力耦合叠加影响导致；二是装机测量参数有限，存在其它影响因素或是装机原因，需要进一步研究。在现有供应商生产能力下的转子动平衡调整范围内，其对电机本体振动加速度的减小贡献量不大。

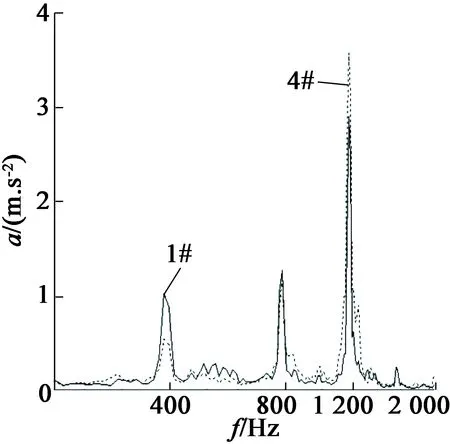
图9 不同转子动平衡下机体振动加速度

4.5 爪极形状对电磁振动影响

图10是不同爪极形状的电机机体振动加速度。在1#样机尺寸上增加爪极极尖的宽度得到5#样机，电机机体36阶振动加速度度峰值明显降低，峰值幅值从2.8 m/s2降低到1.7 m/s2。这样范围内的变动，对发电机的其它性能影响较小，硬件变动不大，在对模具进行调整后能够快速实现量产。爪极结构的改变主要影响励磁磁动势的分布，爪极极尖尺寸的变化改变了爪极之间的间隙，影响式(8)中的Aμ，降低电磁力幅值来减小电磁振动。爪极结构同时也影响着励磁磁场波形与幅值，进而影响到发电机的发电输出性能。极尖尺寸的增大能够减小径向电磁力幅值，也需要考虑其改变对电机发电性能的影响。后期考虑制作不同极尖尺寸的样件进行实验研究。

图10 不同爪极形状机体振动加速度

5 结 语

1) 爪极式发电机的电磁力波谐频率为6kf，发电机机体产生6kf频率的电磁振动时，本电机测试结果存在较为明显的12阶，24阶和36阶振动，其中36阶振动最为严重。

2) 电机负载、定子与转子同轴度和爪极形状对机体36阶电磁振动有显著影响。电机转子动平衡对电机36阶电磁振动影响不明显。

3) 电机机体36阶振动噪声的降低可以通过控制电机负载，定子与转子同轴度和爪极形状3个方面进行优化调整来得到有效控制。