向量在解决几何题型取值范围中的应用探究

福建省莆田市荔城区第九中学 吴明志

“横看成岭侧成峰，远近高低各不同。”对一些问题，如果换一个角度和方法来处理，往往能得全新的一个思路。立体几何和解析几何求取值范围问题历来是高中数学的一个难点，也是近些年高考的一个重要的考点。解决这些问题的时候有时候可能就会遇到很大的困难，这时向量的应用可以为很多题目开辟一个新的思路。可以把向量作为一个桥梁使问题化繁为简，利用向量的模、数量积、夹角之间的关系以及向量不等式等把立体几何或解析几何求取值范围问题转化为我们所熟悉的三角函数、不等式等问题，从而实现问题的解决。在解题的过程中需要构造向量模型，运用向量运算分析进行转化，体现了数学建模、数学运算、直观想象等核心素养和化归的数学思想。笔者结合自身教学经验，分析探究向量在这两种求取值范围题型中的实际应用。

一、向量在解析几何求取值范围中的应用

（一）向量在与三角形、四边形等有关的求取值范围问题中的应用

运用向量法解决此类平面几何求取值范围问题，是向量知识在高中数学解题过程中的重要应用方向，也是灵活运用向量知识解决数学难题的能力的重要体现。它主要是运用向量的定义、几何意义和向量的不等式等来把平面图形中的有关三角形、四边形或者线段等转化为向量的问题或者我们所熟悉的问题，把它作为一个桥梁，优化解题思路。

例1：在直角△ABC 中，∠ABC ＝90°，AB ＝BC ＝2，M，N 为AC 边上的两个动点，且满足|MN|＝，过点M 作BN 的垂线，垂足为D，求BD·BN 的取值范围为________。解析：本题如果直接求解就有一定的难度，但如果我们把所求的问题利用向量的数量积的定义就可以看作是求取值范围，就可以比较容易地解决这个问题了。本题可以先建平面直角坐标系，再设M 坐标，就可以把所求的问题转化，再由二次函数的知识可得取值范围。

（二）向量在圆锥曲线取值范围问题中的应用

高考考查的圆锥曲线取值范围题型有较强的综合性，也是考查的重点。其中向量与圆锥曲线的综合性问题也是考查的重点。求解圆锥曲线取值范围问题最大的思维难点是转化，由于圆锥曲线上的点可以使用相对应的横纵坐标来进行表示，而相应的起点坐标也可以用来表示相对应的向量，所以在这个类型的很多题目中可以利用向量把如两直线夹角中锐角、直角、钝角以及线段长度取值范围等问题转化为我们所熟悉的二次函数、三角函数、不等式等，利用向量自身的范围限制，以及三角函数、不等式范围限制，从而“双管齐下”，突破思维难点。

例2：已知F1、F2是椭圆的焦点，点P 是椭圆上的动点，当∠F1PF2为钝角时，P 横坐标取值范围是多少？本题是通过钝角为出发点来求点的横坐标取值范围，其实这个问题就是涉及直线与直线所成角的问题，其中可分为锐角、钝角和直角或者具体角度等，而平面向量对解决这类问题相对比较容易，所以我们可利用向量夹角公式小于零进行转化，从而解出点P 的横坐标取值范围。

二、向量在高考立体几何求取值范围题型中的应用

立体几何求取值范围问题也是高中数学教学中的难点，而向量可以为问题的解决另辟蹊径，比如对于立体几何的平行垂直与夹角以及距离等问题，都可以通过向量进行直接转化，并运用向量间的相关关系解决，或者也可以先建立空间直角坐标系，再利用向量转化为其他问题，比如函数或不等式等求取值范围来解决问题。

例3：在矩形ABCD 中AB ＝λAD(λ＞1)，将其沿AC 翻折，使点D 到达点E 的位置，且二面角C AB E 为直二面角。F 是BE 的中点，设所求二面角的大小为θ，当λ ∈[2，3]时，求cosθ 的取值范围。解析：本题先建立空间直角坐标系，利用向量的求二面角的方法可以得到

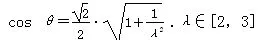
再利用函数方法求取值范围。像这样利用向量转化为我们所熟悉的问题来解决立体几何求取值范围，关键是要找到实现转化为常见问题的求解途径，实现几何问题代数化，从而使问题得到较容易的解决。

综上所述，在高中数学的解析几何和立体几何求取值范围的问题中应用向量的相关知识来转换为我们比较容易解决其他的数学问题有很重要的现实意义。高考考查题型的一大特点是综合性，其题目往往由几种知识点复合而成，其中向量相关知识与这两类几何的融合求取值范围题型是高考考查的重点之一，当我们“山穷水尽”之时如果能灵活运用向量相关知识这个桥梁来解决这两类几何求取值范围题型，会使我们“柳暗花明”。