小学六年级数学应用题教学策略

甘肃省临夏县土桥镇重台塬小学 包德伟

小学数学涵盖的知识包括几何知识、代数知识以及基础统计学知识，虽然小学六年级的数学应用题不会覆盖所有的知识，但是对于六年级学生来说，题目的难度依然较高，教师要通过对应用题中常见难点的研究与分析，了解针对这些难点的教育方法。

一、小学六年级数学应用题的难点

（一）知识点融合较多

高难度应用题最直观的表现为涵盖的知识点类型较多，虽然对于大部分知识来说，允许学生不了解知识点的名称，但是要求其能够解答题目。

目前的教学难点在于，教师如何将这类知识点进行对接和融合，让学生能够在理解题目的情况下选用正确知识点。学生只有具备综合性和融合性思想，比如将代数知识和几何知识进行对接时，才能够更好应对所有类型的应用题。目前的工作问题在于，教师很难在短期内让学生具备这一能力。

（二）学生理解水平较低

一些应用题会通过对语言的使用提高题目的理解难度，对于一些学生来说，由于本身的语言理解能力较差，自然难以找到题目中涵盖的知识点。

对于大部分的学生来说，虽然从表面上来看，分析问题需要学生具有较高的语言理解能力，但事实上学生的逻辑思维决定其能否识别应用题中知识点的融合方法，当学生的逻辑思维能力较差时，其理解水平会大幅度降低，所以教师要对这一内容有清晰认知。

（三）学生知识掌握问题

学生只有在对所有知识有深入把握的情况下，才可在解题中采用正确的方法。当前一些学生学习中的问题在于，由于对各类知识点的把握水平较低，或者对知识的挖掘深度不足等，在解题过程中不敢使用相关的知识点对习题进行解答。

二、小学六年级数学应用题的教学策略

（一）建设思维体系

思维体系的建设中，要求学生能够加强对所有知识点之间关联性的分析，在此基础上让学生能够全面深入地掌握各类知识。对于小学数学教材来说，其包括的综合性知识可以分为三个部分：数据统计部分、代数部分和几何部分。在应用题的教学中，教师可以通过设计融合性习题模式，让学生深度掌握各类知识，并提高知识的关联性。比如教师提出了一个问题：在一个圆形区域内共有100 个人（提出一个概念为“人口密度”，即某区域中人数和这一区域面积的比值），所有这些人中，医生职业的人数占所有人数的20%，教师人数占所有人数的10%，学生人数占所有人数密度的60%，剩余人员的人口密度为5/157，求这一圆形区域的半径。

这一题目的难度较小，但是信息量较多，在解题过程中可提高学生的知识融合能力。题目本身囊括了三部分知识，其中通过对人数比例部分的分析，可让学生回忆平均数部分的知识点；人口密度比值的给出，可以让学生了解代数部分乘除法部分知识点；在圆半径的求取过程中，可以让学生回忆几何部分的各类知识，学生长期接触这类含有多种知识的题目时，其理解能力、知识体系构建能力都会逐渐上升。

（二）建设理解模型

理解模型的建设要求教师能够从知识的具体应用方法角度出发，让学生提高对其内涵的了解水平。

具体的知识讲解和分析过程中，可以通过两种方式提高学生的理解质量，其一为对于该知识的后续延展内容，其二为该部分知识的填充性内容讲解。比如对于平行四边形的面积求法讲解过程来说，在日常授课过程中可通过“填补法”让学生对这一面积求法有更为深入的了解，而之后教师扩展的内容为带领学生对更多图形进行面积求取方法的探索，从而让学生能够通过这一理解模型，在新的知识学习中不断加深对这一理解模型的了解深度。

（三）提高分析能力

分析能力的提高过程要求教师带领学生对其自身的思维缜密程度进行锻炼，采用的方法为：通过对应用题中涵盖知识点以及易错点分析的方式，提高学生的题目分析水平。比如教师设计的某应用题为：

车辆在直线路径上行驶中，其运行方法评价方程为：

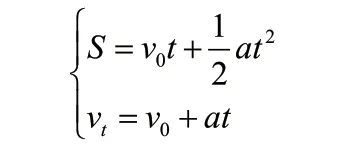
其中t 为车辆的运行时间，a 为车辆的加速度，S 为一段时间内车辆的位移，v0为初始速度，vt为车辆在t 时间内的末速度。现在已知某车辆的加速度为-6m/s2，车辆的初速度为12m/s，问3s 后车辆的位移量。

从速度分析可知，车辆2s 后静止，但是很多学生并未注重对末速度的分析，而是直接采用距离的求取公式计算，最终取得的结果错误。这类习题的练习，可让学生提高自己的思维缜密程度。

综上所述，小学六年级应用题存在的难点包括知识点总量较多、学生的理解能力较差等，在今后的教育工作中，教师要全力规避这些问题，采用的方法包括帮助学生建成理解模型、提高设计题目中涵盖的知识点数量、训练学生的思维缜密程度等。