正弦空间在相控阵雷达设计中的应用

栾铸徵，史厚宝

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

正弦空间是研究阵列天线波束扫描编排与分布特性的数学工具。在球面坐标系研究阵列天线波束扫描时，扫描角偏离法线方向波束将展宽，且展宽与扫描角间的关系非线性。在球面坐标系研究波束排列和栅瓣分布比较困难，因此就希望选择一个方便的坐标系。而在正弦空间中，天线方向图不随扫描角而变化，与扫描角成比例地平移，正弦空间就是单元球面在阵列平面上的投影[1-3]。在参考文献中，一般只给出了正弦空间具备性质的结论，没有结合物理意义给予说明，尤其中文文献分析得较少；所以本文从实际工程应用角度出发，对正弦空间的物理意义给予分析，对一维相控阵雷达、二维相控阵雷达的正弦空间的性质进行了数学推导。通过分析会发现，正弦空间是把形象的波束扫描的三维球坐标空间通过正弦变换压缩到关于扫描角的二维正弦空间，仅保留了角度性质，与距离无关。正是由于相控阵雷达波束扫描特性，相控阵波束排列选择了正弦空间来描述，在正弦空间中有利于描述波束空域覆盖、波束排列及栅瓣分布分析。本文后面给出了正弦空间在雷达工程设计中的应用分析。

1 一维相扫相控阵

如图1所示，对于一个阵元间距为dx的均匀线阵，阵长度L，各向同性阵元辐射的电磁波在空间以满足相干叠加原理合成波束方向图，波束宽度和线阵尺寸成反比，阵列法线的波束宽度可以表示为：

(1)

式中：θ0.5为法线方向波束宽度；λ为波长；k为波束宽度因子，和加权系数有关；L为阵长度。

当波束相对法线方向扫描θ角时，由于波束指向偏移θ角，天线有效孔径是天线法向孔径在波束指向方向的投影，如图1，孔径由L变为L′，由式(1)可知，扫描角波束宽度为：

L′=L·cosθ

(2)

(3)

图1 一维线阵扫描示意图

波束宽度变化与扫描角的余弦函数成反比，现将扫描特性在单位半圆上研究，如图2所示，单位半圆上研究的特点是，圆弧长度就是弧度表示的角度，阵列法线方向波束扫描的过程就是由AB扫描到A′B′，波束宽度在阵列平面的投影分别为MN、M′N′，下面研究投影的特征。

图2 单位圆波束正弦投影示意图

如图2，在法线波束方向，波束边点A和B在线阵投影可以表示为MN，有如下关系：

MN=sinθA-sinθB=sin(θ0.5+)-sin(-θ0.5-)=

(4)

根据正弦函数的泰勒展开公式有：

(5)

从而有：

(6)

而：

(7)

有：

(8)

当忽略高阶无穷小后，有：

α0.5=MN=sin(θ0.5)

(9)

可见，法线波束宽度在阵列平面投影可以用波束宽度角度正弦表示。同时波束相对法线扫描θ角度后的P点，指向OP投影也用正弦表示为：

α=OP′=OP·sinθ=sinθ

(10)

(11)

A′B′在X轴投影为M′N′，该投影刻画了波束扫描展宽特性，有：

(12)

根据泰勒展开公式有：

(13)

从而有：

(14)

根据式(4)得到：

(15)

当忽略高阶无穷小后，有：

α0.5=M′N′=sin(θ0.5)=MN

(16)

可见波束相对法线扫描时，波束在单位圆内运动，波束扫描角正弦就是在阵列平面的投影，代表波束指向；法向波束宽度的正弦可以表示波束宽度在阵列平面的投影，并且扫描后波束宽度在阵列平面的投影长度和法线波束在阵列平面投影相等，和波束扫描角无关。由公式(12)可见，这种特性的主要原因是：波束扫描后波束展宽与扫描角余弦成反比，而扫描波束宽度在阵列天线的投影和扫描角余弦成正比，形成互逆关系从而产生相互抵消效应。可见，正是波束扫描的这种展宽特性与阵列平面投影特性相结合，产生了正弦空间的特征。

公式(15)高阶小的忽略，会引起误差，用扫描后波束边角在正弦空间的投影，相对法线波束宽度正弦值，两者的差与法线波束宽度正弦归一化的一半表示误差的大小，即：

(17)

该误差大小表征了相邻波束间波束的交叠程度,误差曲线仿真条件如下：法线波束宽度3°，从法线扫描到70°，误差变化过程如图3所示。由于误差数值极小，采用对数(dB)表示。

图3 一维线阵正弦空间误差曲线

可见在该仿真条件下，阵列天线扫描后的波束正弦投影产生的交叠极小(小于1/2 000),可以认为等于法线波束宽度正弦。根据公式(15)可见，在扫描角60°时有一个下凹口(因为三阶量为0)。在波束扫描过程中，波束指向没有误差,但相邻3 dB波束宽度间有交叠,并且波束交叠量在工程应用可以忽略，所以正弦空间消除了波束扫描后展宽的影响，可用于研究波束空域覆盖和波束排列。

2 二维相扫相控阵

2.1 二维正弦投影分析[1-6]

为了形象地描述正弦空间的物理意义，研究二维相控阵按照矩形分布在XOY平面，如图4所示。在X轴向间距dx，阵元数N，在Y轴向阵元间距dy，阵元数M，阵列的法线指向OZ，即取正半球。

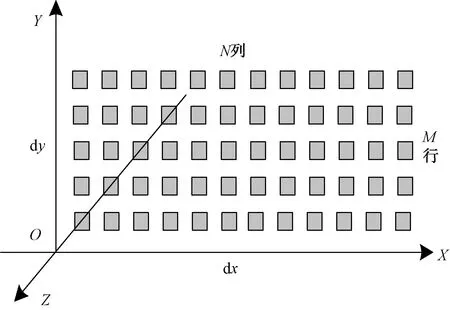
图4 二维阵列布阵图

在一维相控阵中波束扫描角定义为与阵列法线方向OZ的夹角，但是在二维相控阵中，波束指向与法线方向只有一个夹角，难以定位波束空间指向，所以按与X、Y轴夹角定义，假设波束指向OP，OP与X轴间的夹角θ′为方位角，OP与Y轴间的夹角φ′为仰角，如图5所示。

图5 三维空间波束指向立体图

现分析在该夹角定义下，波束扫描特性，阵列分布在XOY平面，首先求单位向量OP在XYZ各坐标轴投影，由于已知P点与X、Y轴夹角，所以投影分别为：

(18)

P向Z轴的投影是通过P点在XOZ平面的投影P′，∠PxOP′为φ，根据立体角关系：

∠POP′=π/2-φ′

(19)

cosφ=cos(π/2-φ′)·cosθ′=sinφ′·cosθ′

(20)

(21)

从而求出单位向量OP指向在直角坐标系中各坐标轴的分量。而阵列中每一个阵元矢量坐标可表示为：

Amn=(ndx，mdy，0)

(22)

式中：n∈[1,2，…,N]；m∈[1,2，…,M]。

阵元相对坐标系原点的波程差，是阵元在OP指向的投影，即阵元矢量与波束指向矢量的内积：

Lmn=Amn·P=ndx·cosθ′+mdy·cosφ′

(23)

上式中，当θ′固定，而φ′连续变化时，波束指向与X轴、Y轴夹角分别为：

cos(∠XOP)=X·P=1·cosθ′+0·cosφ′+

cos(∠YOP)=Y·P=0·cosθ′+1·cosφ′+

可得：

∠XOP=θ′

(24)

∠YOP=φ′

(25)

可见，波束指向与OX轴夹角不变，说明波束指向是在与OX轴夹角为θ′的圆锥曲面上运动。如图6所示，即绕OX轴上圆C从Q点运动到P点，且从波束扫描围绕圆锥运动可知波束也分布在圆锥曲面上，同时说明了，如果仅在仰角φ′方向做数字波束形成(DBF)，那么多波束是分布在一个圆锥曲面上，而不是一个扇形的平面上。同理，当仰角φ′不变，而θ′连续变化时，波束指向按照与OY夹角为φ′圆锥曲面做运动，即绕OY轴上圆D从B点运动到P点。

图6 双圆锥曲面运动扫描图

下面对方位角θ′固定、仰角φ′扫描运动时的波束扫描特性进行分析，由上述可知，波束指向OP在圆锥曲面C上运动，如图7所示。

图7 圆锥曲面分析正弦空间示意图

该圆锥曲面PCQ与坐标平面YOZ夹角为θ，且圆锥上圆C在YOZ面投影为AOM，则：

θ=π/2-θ′

(26)

则∠QOA=∠POM=θ，OP运动期间在X轴的投影长度等于OP与YOZ平面夹角的正弦，即：

α=PM=AQ=sinθ

(27)

因为扫描角θ理论上可以取±90°，所以上式的取值范围为[-1,+1]。同理定义仰角φ，即图8中圆锥曲面BDP与坐标平面XOZ夹角为φ，则：

φ=π/2-φ′

(28)

OP在Y轴的投影长度等于OP与XOZ平面夹角的正弦，即：

β=BE=sinφ

(29)

扫描角φ理论上也可以取±90°，所以取值范围也是[-1,+1]。

从而重新定义二维阵列扫描角θ，φ，基于圆锥曲面定义的角度，其中θ表示波束指向与坐标平面YOZ的夹角，φ表示波束指向与坐标平面XOZ的夹角。该夹角的正弦就是波束指向角分别在OX、OY轴的投影，也就是波束在阵列平面的投影。从上述论证过程可以看出，波束扫描角与OX、OY轴夹角的定义，和波束指向与XOZ、YOZ平面夹角呈互为余角的关系；后面将会发现，与OX、OY轴夹角更有利于工程应用分析，但是用与OX、OY轴夹角定义，会出现波束指向角阵列投影呈余弦关系，波束宽度投影是正弦关系，不统一，所以不宜采用。

在新的定义下，阵元在OP方向的投影为：

Lmn=Amn·P=ndx·sinθ+mdy·sinφ

(30)

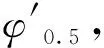
(31)

根据公式(12)～(16)可得：

β0.5=sinφ0.5

(32)

从而可知，波束仰角向扫描时，波束宽度在OY轴向的投影等于仰角在法向的波束宽度φ0.5的正弦，由于方位角和仰角取值的一般性，可见仰角波束宽度投影不随仰角和方位角扫描的变化而变化。

同理可以证明，仰角φ一定，方位角θ扫描时，波束指向和波束宽度在图8中圆D上做圆锥扫描运动，由B点运动到P点，方位角波束宽度分布在圆D上，波束指向和波束宽度仍然满足和仰角相似的性质，即波束指向在OY轴的投影就是波束仰角的正弦值，波束宽度的投影就是法线方向的波束宽度，即：

仰角指向在Y轴投影为：

β=sinφ

(33)

方位波束宽度在X轴投影为：

α0.5=sinθ0.5

(34)

从而有，当波束空间指向OP时，单位球空间内，P点在阵列平面XOY的投影有如下关系：P点在阵列XOY投影正弦坐标为(α，β)，仰角波束宽度正弦投影长度为β0.5，方位波束宽度正弦投影长度为α0.5，从而可得二维波束扫描在阵列空间的投影如图8所示。

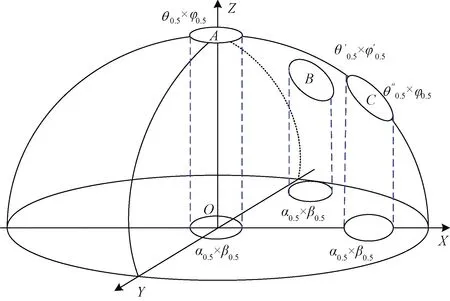
图8 二维波束扫描阵列平面投影图

可见，波束指向OA、OB和OC时，波束在阵列平面的投影是不变的，位置等于正弦空间定义方位角和仰角的正弦，波束宽度投影等于阵列在法向波束宽度的正弦。从而形成了方位角和仰角扫描的正弦坐标系，是一个二维坐标系，在该坐标系中波束扫描由非线性运算转换成了加减线性运算。

2.2 正弦空间波束排列分析

从图7还可以看到，当波束方位角指向θ，仰角从0°逐渐增加时，就是波束从Q点逐渐运动到P点，当P点运动到XOY平面时，仰角达到最大值：

φmax=π/2-θ

(35)

同理，方位角最大值为：

θmax=π/2-φ

(36)

当仰角为φ时，方位角沿着圆锥面扫描，最大值取为π/2-φ，此时正好是仰角φ扫描的边界，两角关系互为余角关系，所以有：

β2+α2=sin2φ+sin2θ=sin2φ+

sin2(π/2-φ)=sin2φ+cos2(φ)=1

(37)

由于φ是任意设定的，在数学上扫描角度取值范围为[-90°,+90°]，所以正弦空间的扫描边界是一个单位圆，所有波束都在一个单位圆内，如图9。此圆为实空间，波束被规范在该区间内，也就是把单位正半球映射到单位圆内。

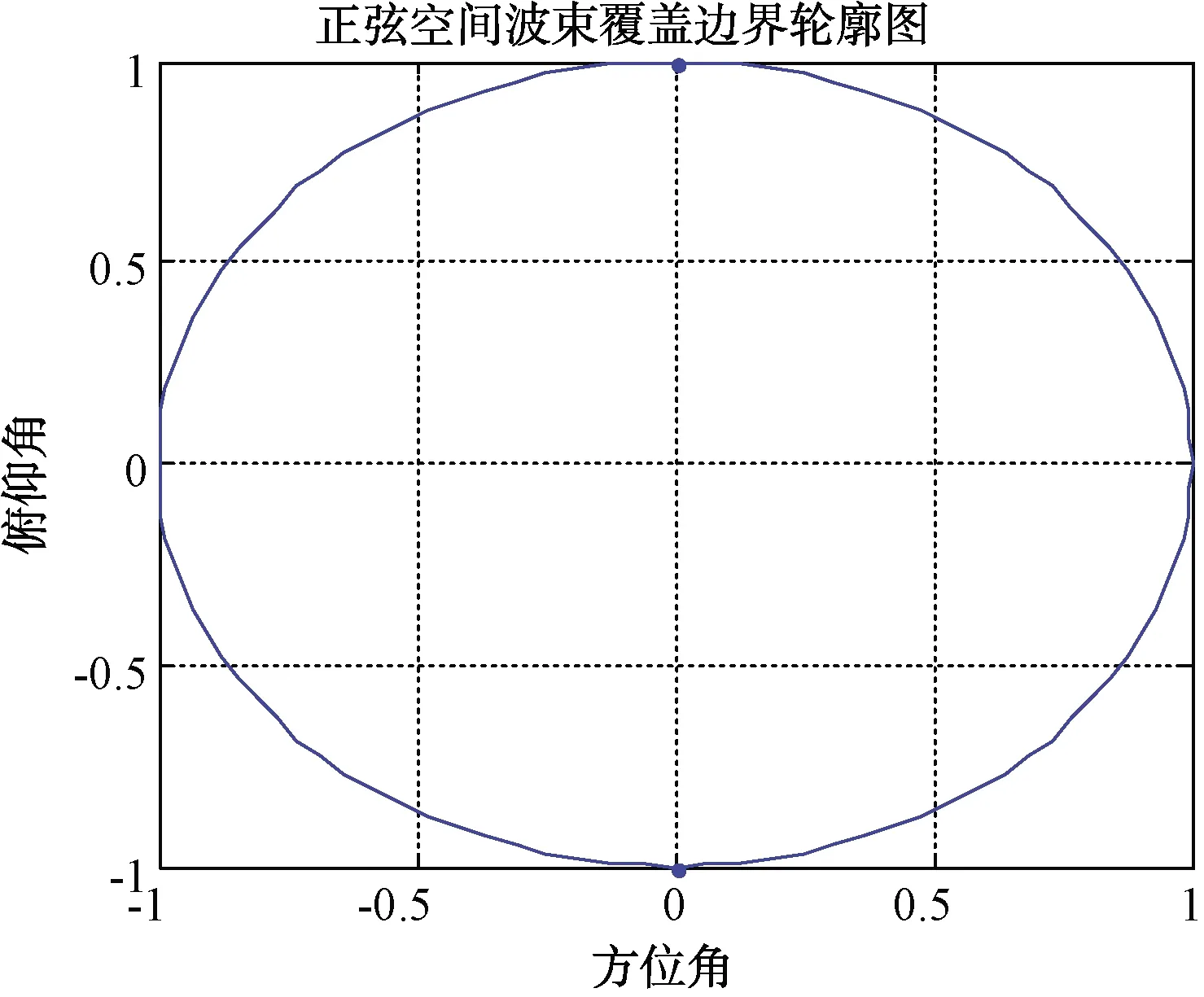
图9 实空间部分图

单位圆是理论上的波束扫描最大范围，而实际上，波束不会扫描到±90°，而会根据天线本身特性和实际工程需要，在实际工程应用的球面坐标系波束扫描空间向正弦空间投影形成一个区域。该区域上对每一个方位角，仰角有一个范围φmin～φmax，对应正弦坐标为sinφmin～sinφmax，根据式(32)、(34)，波束宽度在正弦空间是一个不变量，即仰角法线波束宽度的正弦，而仰角扫描范围和法线波束宽度已知，从而仰角向波束排列波束数量为：

(38)

同理可以证明，仰角一定，方位角波束排列数为：

(39)

假设在球坐标系方位覆盖±45°，仰角覆盖±40°条件下，方位角2°、仰角3°的条件下，正弦坐标系波束覆盖及波位编排如图10所示。

图10 波束编排图

2.3 正弦空间栅瓣特性分析

在阵列扫描特性中，栅瓣是阵列设计的重要指标，栅瓣的出现是由于阵列天线中阵因子的周期性而产生的旁瓣电平，该旁瓣电平和主瓣特性一致，由于周期性而产生了镜像波束，波束宽度和增益相同，导致雷达产生测向模糊，并且主瓣增益下降3 dB，严重影响雷达威力覆盖范围。栅瓣的出现条件是相邻单元波程差出现周期性引起的，如图11所示。

图11 栅瓣分析阵列布阵图

阵列法线方向A1P，假设波束扫描角为θ0，根据图11几何关系，可得相邻阵元波程差为：

L0=dx·sinθ0

(40)

假设此时栅瓣出现的位置为θ1，则在该方向的相邻阵元波程差为：

L1=dx·sinθ1

(41)

栅瓣出现是由于周期性，栅瓣指向的相邻单元波程差和波束指向的相邻单元波程差的差是射频波长的整数倍，即：

L1-L0=dx·sinθ1-dx·sinθ0=

dx(sinθ1-sinθ0)=mλ

(42)

式中：m=0，±1，±2，…,可见扫描角为θ0时，栅瓣的位置θ1是确定的、可预测的。

令αm=sinθ1，α0=sinθ0，则可得：

(43)

栅瓣指向角的正弦αm的取值也是[-1,+1]，但根据上述数学公式，以及m的取值，αm可能在大于1的位置界外，这在实际物理空间上是不存在的。此时栅瓣出现是数学推导的结果，是在虚空间；但是如果取值出现在扫描的实空间，则就会出现栅瓣。虚空间和实空间的波束是一一对应的。

式(43)中，m=0时为波束扫描实空间，m=±1，±2，……时，为出现栅瓣的虚空间，要使栅瓣不出现，由于m可以取正负，那么至少m的取值要小于1，所以根据式(43)有布阵间距：

(44)

上式中，当等号成立时出现栅瓣，要使栅瓣不出现，dx需要取小于号。由式(43)可知，当栅瓣θ1最大位置取90°，最大扫描位置θ0=θ0max，最小波长λ=λmin(最大工作频点)时的布阵间距是dx的取值上限，要使阵列扫描不出现栅瓣，此时布阵间距应为：

(45)

而在矩形布阵的二维相控阵雷达中，方位和俯仰扫描角是相互独立的，所以仰角栅瓣和方位角的栅瓣位置相互独立，仰角栅瓣位置及布阵间距为：

(46)

(47)

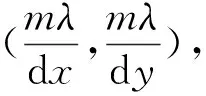
例如10 GHz，方位俯仰角按45°扫描布阵，栅瓣图分布如图12所示。

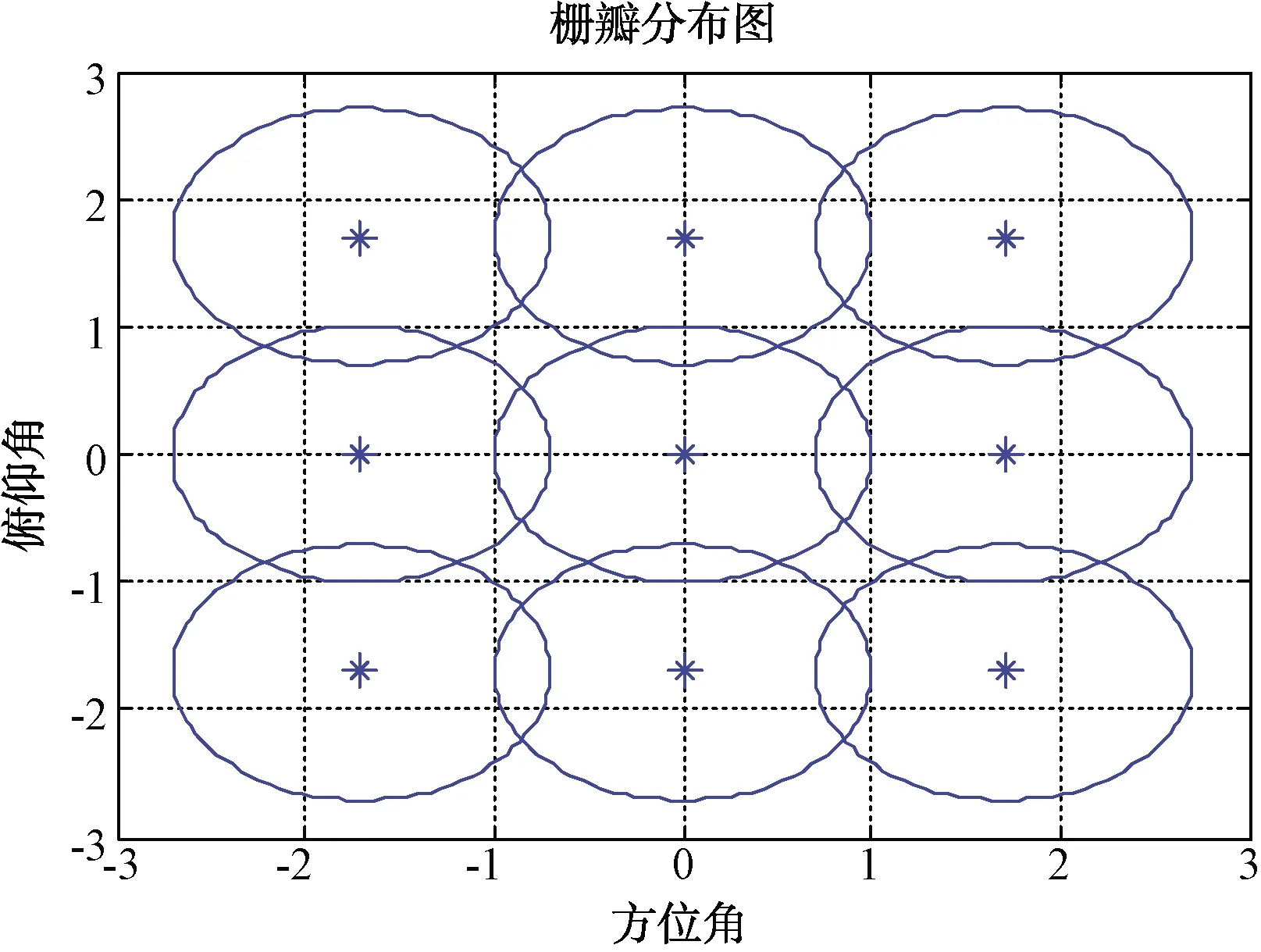
图12 栅瓣分布图

3 工程应用

在实际工程应用中，波束扫描空域是在大地球坐标系(球坐标系)描述，波位排布及栅瓣分析是在阵列空间进行，需要建立球坐标系和阵列正弦空间的一一映射关系。见图13，阵列天线在XOY平面，波束法线在OZ轴，波束扫描如图13所示。多功能相控阵雷达按平台性质有2种：一种是陆基、车载固定平台，另一种是舰载、机载摇摆平台。这2种雷达由于平台不同，对阵列天线的扫描特性要求也不同。

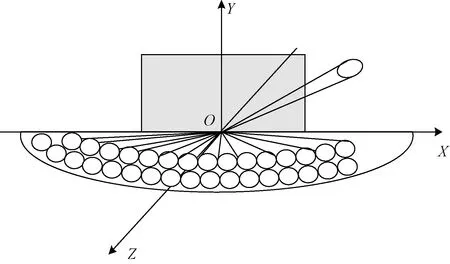
图13 工程应用波束扫描示意图

如图14，大地坐标系为OX′Y′Z′，阵列坐标系OXYZ，当不发生摇摆时，两坐标系重合，阵列坐标系发生姿态变化，可分解为纵摇、横摇和方位旋转。

图14 阵面旋转坐标系示意图

大地坐标系下，阵列平面在XOY′平面，阵面法线方向在OZ′，波束指向OP(方位角θ′，仰角φ′)在OX′Y′Z′坐标系内表示如下：

(PX′，PY′，PZ′)=(cosφ′sinθ′，sinφ′，cosφ′cosθ′)

(48)

当阵列坐标系发生纵摇旋转或纵摇倾斜ξ角时，Y′OZ′平面旋转到YOZ，由Z向Y轴旋转角度为正，P点在X轴投影不变，为cosφ′sinθ′，P点在Y′OZ′投影P′点，在坐标系经逆时针方向旋转ξ角，达到新的坐标，所以新向量在阵列坐标系可以表达为：

OP′XYZ=OP′X′Y′Z′·e-jξ

(49)

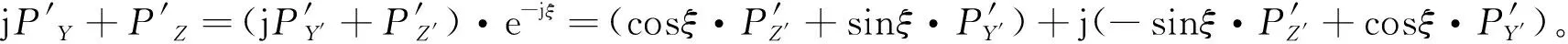
从而在纵摇发生时，大地OX′Y′Z′坐标系到阵列OXYZ坐标系，波束纵摇变换矩阵为：

(PX，PY，PZ)T=Tξ(PX′，PY′，PZ′)T

(50)

同理，当OX′Y′平面发生横摇旋转φ时(OX′向OY′方向旋转角度为正)，横摇变换为：

(PX，PY，PZ)T=Tφ·(PX′，PY′，PZ′)T

(51)

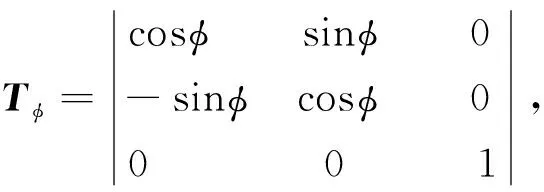
当在OX′Z′发生方位角旋转η(OZ′向OX′方向旋转角度为正)时，波束方位角变换矩阵为：

(PX，PY，PZ)T=Tη·(PX′，PY′，PZ′)T

(52)

在实际工程应用中，阵列天线根据不同的应用，放置在不同的位置，该位置最终会分解为一定的横摇、纵摇及方位旋转组合运动而成的变换。

3.1 固定平台雷达

固定平台雷达是指雷达所在平台在使用中是不动的，用于对指定空域波束覆盖，例如美国爱国者系统中的MPQ-53雷达，机动式部署萨德系统中的TPY-2雷达(如图15所示)，以及铺路爪FPS-115雷达，均属于现役的固定平台雷达。

图15 萨德系统中的TPY-2雷达

对于固定阵，如图16所示，阵面在大地坐标系OX′Y′Z′的X′OY′平面，阵面倾斜相当于大地坐标系OX′Y′Z′产生一个纵摇倾角，阵面倾斜ψ角，阵面在XOY，阵面法线方向为OZ，雷达在大地坐标系的空域指向OQ的方位角θ′，仰角φ′。

图16 固定阵和大地坐标系

根据角度定义，则Q点在大地坐标系中的坐标表示为Q(X′,Y′,Z′)。阵面倾角为ψ，等价于阵面发生纵摇角ψ，根据纵摇变换式(50)可知，波束指向OQ在阵列坐标系时坐标为Q(X,Y,Z)：

Q(X,Y,Z)=Tξ(ψ)·Q(X′,Y′,Z′)

(53)

根据正弦空间角度定义可知，矢量OQ与OX、OY轴的夹角就是阵面正弦空间角度定义的余角，所以可以得到阵列坐标系方位角θ和仰角φ的表达式为：

cos(π/2-θ)=QX=cosφ′·sinθ′

(54)

cos(π/2-φ)=QY=

sinφ′·cosψ-cosφ′·cosθ′·sinψ

(55)

从而有：

θ=π/2-arccos(QX)

(56)

φ=π/2-arccos(QY)

(57)

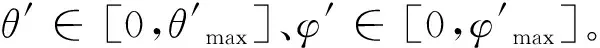
仿真条件：固定阵工作在频率10 GHz，阵面法线波束宽度方位2°，仰角3°，阵面倾斜20°，方位角扫描±60°，仰角覆盖70°。根据上述分析：在阵列坐标系方位最大扫描角为60°，方位最大角度确定阵列方位向阵元间距。而仰角最大扫描角为55.54°，按照仰角最大角度确定阵列仰角向阵元间距。从而根据大地空间扫描范围和法线波束宽度，得到波位排布(如图17所示)，再通过阵元间距可以得到栅瓣分布(如图18所示)。

图17 固定阵正弦空间波束排布图

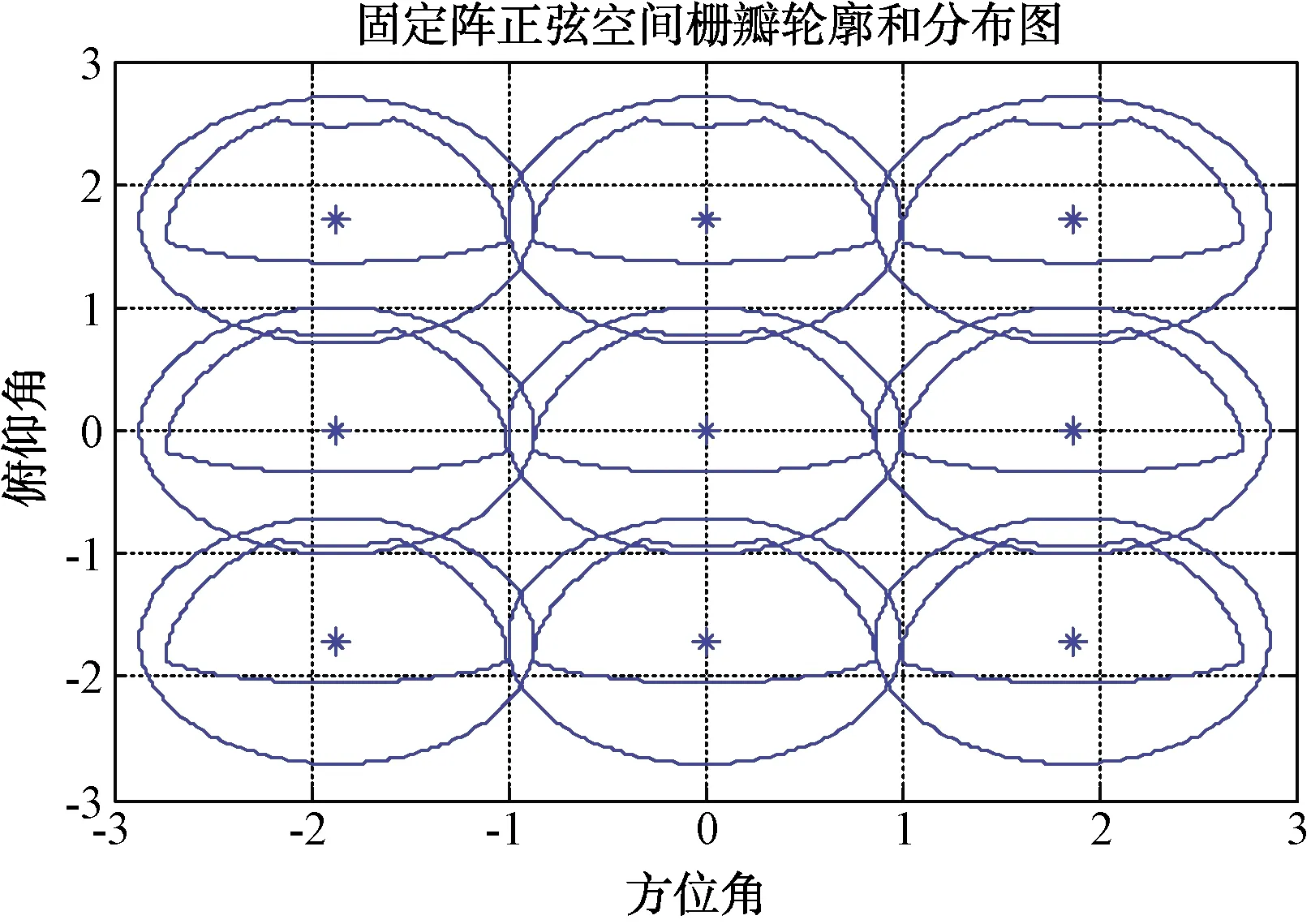
图18 正弦空间栅瓣分布图

在正弦空间根据式(32)、(34)得到每一个波位大小为sin2°·sin3°，根据式(56)、(57)得到波束扫描范围，根据式(38)、(39)得到排布如图17所示。

根据阵元间距和公式(43)、(46)得到栅瓣分布如图18所示，实际上是图17的轮廓平移。

3.2 摇摆平台相控阵雷达

摇摆平台雷达是指雷达所在平台在使用中是摇摆运动的，舰载和机载雷达属于摇摆平台应用的雷达，要求在摇摆条件下，波束仍然具备大地空间空域覆盖能力。舰载雷达在舰船上的布置有在首尾左右舷的，例如提康德罗加级巡洋舰中SPY-1和欧洲的APAR；有布置在左右舷前后45°角的，例如阿里伯克级驱逐舰的SPY-1(如图19所示)。每一种雷达空间布置对阵列天线设计的影响不同。

图19 阿里伯克级驱逐舰SPY-1雷达

现在以舰载左舷前方45°角布阵来分析，要设计阵列，首先把波束在大地坐标系的空域覆盖范围映射到阵列空间，从而用正弦坐标系对阵列进行设计，得到波束扫描边界、波位排布及栅瓣分布特征。

如图20所示，波束在大地坐标系OX′Y′Z′的指向OP′(仰角为φ′，方位角为θ′)，需要变换到阵列坐标系OXYZ，大地坐标系和阵列坐标系之间有几层空间坐标系变换，这种几何空间变换可以拆分成大地坐标系-甲板坐标系-阵列坐标系的转换，舰船摇摆体现的是大地坐标对甲板坐标系的影响，而甲板坐标系和阵列坐标系体现了相对的空间几何结构关系，从这个分析角度出发进行分析。

图20 大地空间和阵列摇摆空间图

在没有发生摇摆时，甲板坐标系和大地坐标系重合，假设舰艏指向东为Z轴，左舷指向南为X轴，Y轴指向天。首先大地坐标系空间指向OP′，发生纵横摇摆后，波束在甲板坐标系坐标发生变化，而阵列坐标系相对于甲板坐标系是发生了方位旋转η角和阵面倾角ζ，按照上述运动分解，可得到变换如下：舰船发生纵横摇时，大地坐标系指向OP′经纵摇变换式(50)和横摇变换式(51)后得到甲板坐标，即：

OPS=Tφ·Tξ·OP′

(58)

阵列坐标系相对于甲板坐标系相当于阵列首先发生方位旋转η(式(52))，再发生阵面倾斜ζ，阵面倾斜相当于纵摇变换式(50)，所以有：

OP=Tξ(ζ)·Tη·OPS

(59)

从而得到阵列坐标系和大地坐标系的变换关系：

OP=Tξ(ζ)·Tη(η)·Tφ(φ)·Tξ(ξ)·OP′

(60)

式中：OP为阵列坐标系下的矢量；OP′为大地坐标系下的矢量。

矢量OP和X、Y轴的投影就是阵面正弦空间角度的余角，所以可以得到阵列坐标系方位角θ和仰角φ的表达式为：

cos(π/2-θ)=PX

(61)

cos(π/2-φ)=PY

(62)

从而有：

θ=π/2-arccos(PX)

(63)

φ=π/2-arccos(PY)

(64)

得到阵列坐标系的θ，φ。仿真条件是频率为3 GHz，阵面法线波束宽度方位角2°，仰角4°，阵面位于舰船左舷前部面阵，阵面倾角ζ为20°，方位旋转角η为45°，横摇角φ为15°，纵摇角ξ为8°。阵面大地空间空域方位覆盖±45°，仰角覆盖70°。计算得到，当纵摇角8°，横摇角15°，仰角0°时，方位角在阵列坐标系方位需要扫描到最大值46.4°,按照扫描角48°设计方位间距；当纵摇角-8°，横摇角-15°，方位角0°时，仰角在阵列坐标系需要扫描到最大值69.68°,按照70°设计仰角间距。

从而方位按48°，仰角按70°扫描布阵，在正弦空间根据式(32)、(34)得到每一个波位大小为sin2°·sin4°，根据式(63)、(64)得到波束扫描范围，根据式(38)、(39)得到排布，如图21所示。

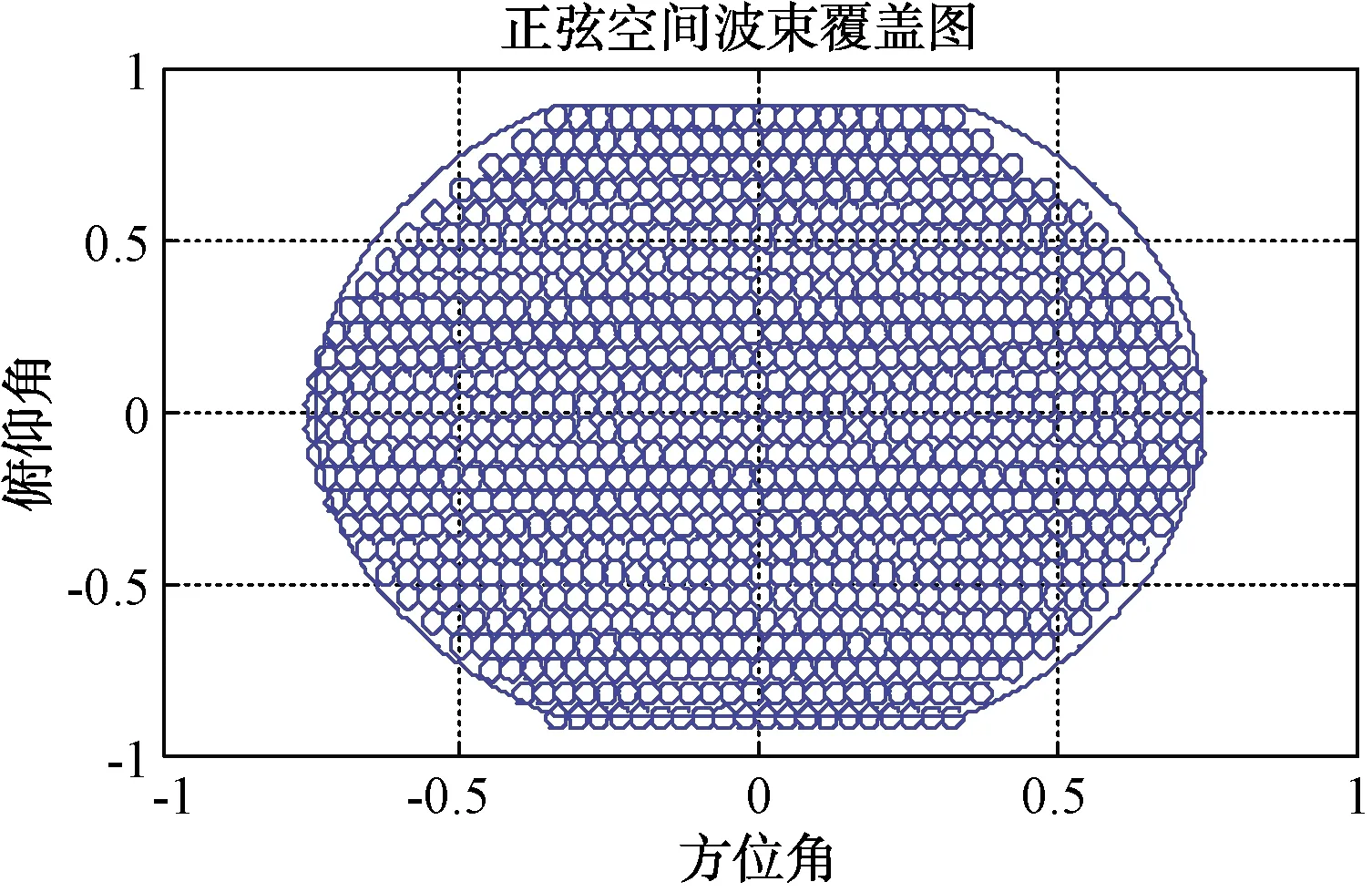
图21 摇摆阵正弦空间波束覆盖及排布图

图21包含了雷达在纵横摇发生时，阵列空间波束空域覆盖需要具备的能力。摇摆发生时，大地空域覆盖就在该阵列空域图21内移动。

根据该布阵间距和公式(43)、(46)得到栅瓣分布图，纵摇8°、横摇15°时的栅瓣分布图如图22所示。

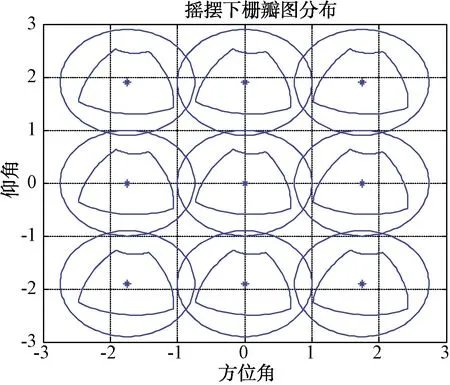
图22 纵摇8°、横摇15°栅瓣分布图

在纵摇-8°、横摇-15°时的栅瓣分布图如图23所示。

图23 纵摇-8°、横摇-15°栅瓣分布图

图22和图23表示舰船摇摆时，雷达在阵列空间探测空域范围就是在图21内移动的过程。

4 结束语

正弦空间不论是在雷达论证时还是雷达装备工作时，都是有力的应用工具，论证时应用于波束空间排布和栅瓣分布分析。在正弦空间，波束指向和波束宽度不用度、弧度来描述，而用弧度的正弦(波束指向)或正弦增量(波束宽度)来表达，波束宽度在正弦空间不随扫描角变化。雷达在大地坐标系(球坐标系)确认波束扫描范围，在正弦空间研究波束排列和栅瓣分布，应用正弦空间论证阵面规模，论证资源调度。在雷达装备工作时，由于探测任务而需实时解算波束在指定空域内的扫描和波位排布，正是正弦空间为这种解算提供了便利条件。