重力异常变密度界面深度反演方法对比

袁永祺，贾 真

(成都理工大学 地球物理学院，四川 成都 610059)

1 引 言

界面深度反演是重力异常定量地质解释的常用方法，被广泛应用于沉积盆地基底起伏和莫霍面形态的相关研究。根据算法的具体实现途径可以将界面深度反演方法划分为频率域反演和空间域反演。频率域方法最早是由Oldenburg[1]基于Parker[2]推导的频率域重力异常正演公式提出的。该方法最早是针对二维界面深度的反演。后来，Granser[3]、Chai 和 Hinze[4]利用指数密度深度函数将该方法推广到三维沉积盆地深度反演中。

关于空间域密度界面深度反演方法，Bott于1960年提出了一种根据重力异常计算二维沉积盆地基底深度的方法[5]。该方法以无限大均匀水平物质层重力异常公式为基础，通过迭代不断调整数据点正下方的物质层的深度，使得模型响应逐次逼近观测重力异常。后来，一些学者考虑到了在实际地质条件下由于压实作用造成密度随深度变化，提出了变密度界面深度反演算法，并给出了不同的密度模型，包括指数衰减模型[6-9]、双曲函数衰减模型[8,10,11]、线性模型[12-15]、二次函数模型[16-18]以及多项式模型[19,20]。由于阶梯状的棱柱模型不能精确地刻画界面的精确形态，Guspí[19]采用了相对光滑的多边形截面二度体作为反演模型。针对这种模型，后来，Zhou[21]提出了密度随深度和水平位置变化的反演方法。

由于盆地基底实际上更接近于分段的连续三维表面，二维假设并不总是成立的。Cordell和Henderson[22]提出了一种三维界面反演方法。为了加快计算速度，重力异常计算点正下方界面单元为直立长方体，其他位置的界面单元为有限长的线质量。此后，在讨论三维和2.5维反演的文献中，学者们都是以直立长方体作为构造界面模型的基本单元[22-25]，相应的反演方法以Bott法[22,25,26]和非线性反演[22-24]为主。另外，还有学者提出利用拟退火算法[27]进行界面反演。

尽管截至目前学术界已经提出过多种界面深度反演方法，但对不同方法的比较分析还相对较少。因此，本文基于模型试验对Bott法和非线性反演的计算效率和适用性进行了详细的讨论和分析。

2 密度界面深度反演数学原理

2.1 密度界面模型及其重力异常的计算

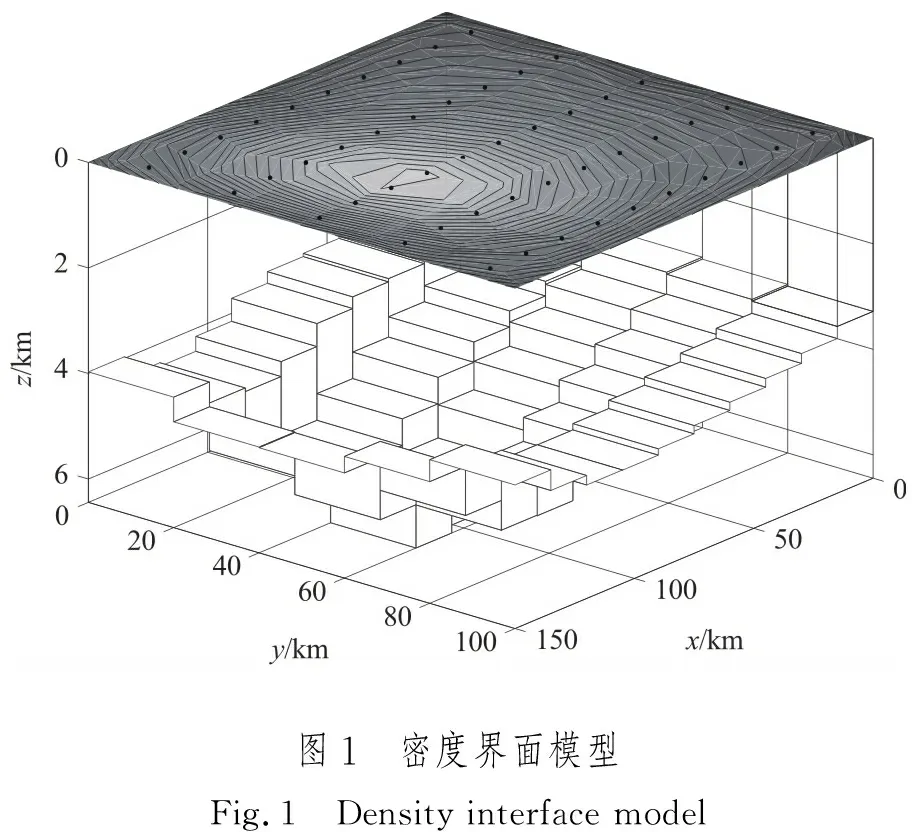
作为研究对象的密度界面位于密度均匀的基底和密度随深度变化的盖层之间。密度界面是用相同大小的矩形来刻画的，每个矩形对应着一个直立长方体(图1)。在长方体内部，密度随深度按以下函数关系变化[24]：

(1)

式(1)中，z为深度(km);Δρ0和Δρ(z)分别为地表和深度z上的剩余密度(g/cm3);α为常数。Δρ(z)和α的具体取值需要通过其他先验信息(例如测井)确定。关于密度随深度按照式(1)变化的直立长方体产生的重力异常，Chakaravarthi等人[24]给出了具体的计算方法，即将所有直立长方体的贡献累加起来，就可以得到整个密度界面的重力异常。

2.2 反演算法

对于重力异常的界面反演，学者采用了两种反演策略。一种是基于无限水平薄板的迭代算法，无需求解线性代数方程组，另一种是通过将非线性问题线性化并增加正则化因子保证方程稳定的传统非线性问题求解方法。

2.2.1 Bott法

在Bott法的反演计算过程中，界面单元中心点必须与重力数据点位于同一水平位置(图2a)。

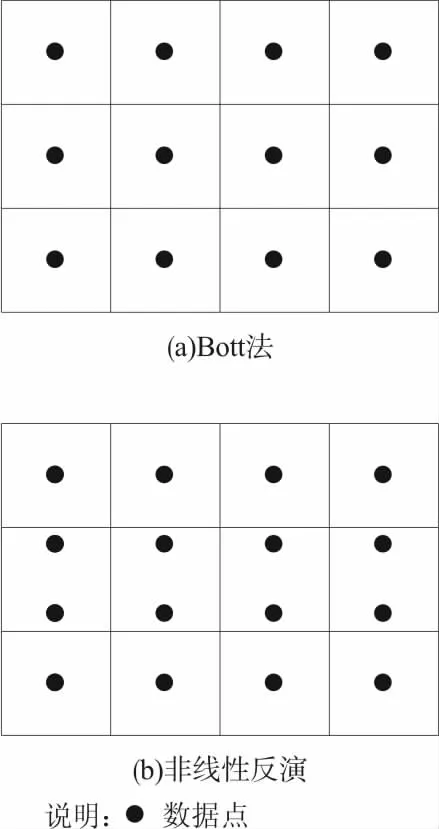
图2 两种反演方法对密度界面单元与观测点之间关系的要求Fig.2 Prerequisite for the position of the gravity station and the interface elements

界面初始深度由(2)式确定[24]：

(2)

式中，(xi,yi)为第i个界面深度点和重力数据点的水平位置；gobs为观测重力异常；Δρ0和α的含义同式(1)。求出界面深度初始值之后，再按照式(3)迭代求取界面深度：

(3)

式(3)中，G=6.67×1011N,m2/kg，为万有引力常数；Δgcalc为界面密度模型的重力异常响应;zk和zk+1分别为第k次迭代前后的界面深度。如果达到指定的迭代次数，或者模型响应与实测数据的拟合差低于预先定义的阈值，则终止迭代[10]。

2.2.2 非线性反演

不同于Bott法，非线性反演方法对数据点的水平位置没有特殊要求(图2b)。该方法以界面深度为反演变量。为了保证反演过程的稳定性需要引入额外的约束条件。本文采用的数学手段是吉洪诺夫正则化。引入约束条件后的反演问题可以表示为下面的最优化问题[28-30]:

(4)

式(4)中，z为所有界面节点深度构成的向量;d和g分别为观测异常和模型响应;λ>0为控制约束条件的正则化系数;z0为界面深度初始值。由于界面深度与重力异常是非线性关系，式(4)所表示的最优化问题可以通过高斯牛顿法求解。模型修正量通过式(5)计算：

Δzi=[JTJ+λITI]-1JT[d-g(zi)]

(5)

式(5)中，Δzi为第i次迭代计算后得到的模型增量，J为雅可比矩阵，I为单位矩阵。更新后的界面深度可以通过式(6)计算：

zi+1=zi+Δzi

(6)

式(6)中，zi+1和zi分别为第i次迭代前后的界面深度。

3 合成模型测试

为了对两种算法进行对比分析，本文采用了一个水平尺度为300 km×400 km的界面模型(图4a)，并按照2.1节中介绍的方法计算了重力异常 (图4b)。界面以上的剩余密度按式(1)随深度变化。这里，Δρ0=-0.5 g/cm3，α=0.171 1(图3)。

图3 剩余密度随深度的变化Fig.3 Remnant density variation with depth

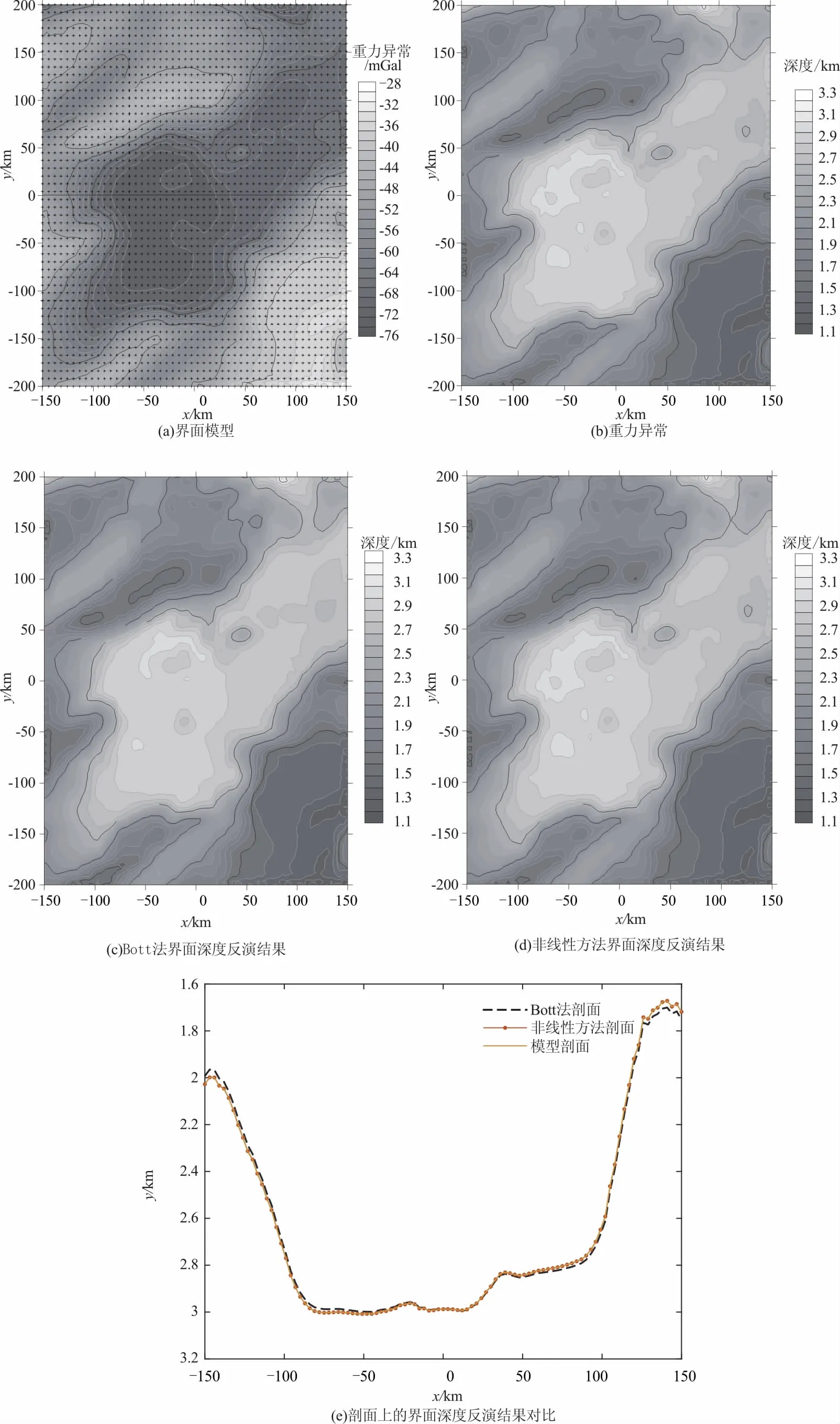
图4 密度界面模型及其深度反演结果(剖面位置见(a)、(c)、(d))Fig.4 Density interface model and depth inversion results

图4中展示了分别采用两种反演算法所得到的计算结果。从图中可以看出，两种方法的反演效果十分接近。这里，x和y方向的界面节点个数分别取40和56。反演过程以模型响应与观测异常之间的拟合差(2-范数)小于100 mGal作为循环终止条件。在该条件下，Bott法和非线性方法的迭代次数分别为5次和3次(图5)。这表明：若单独以迭代次数作为评判标准，则非线性方法的收敛速度优于Bott法。但是，在拟合差不变的情况下，Bott法反演的总耗时却小于非线性方法，暗示后者单次迭代耗时比前者要多。

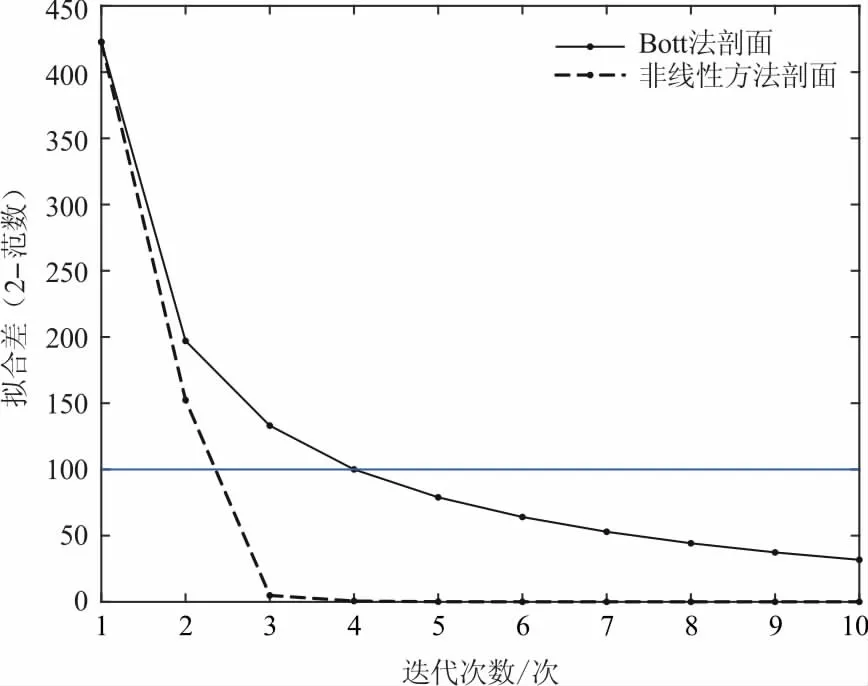
图5 Bott和非线性方法收敛速度的比较Fig.5 Comparison of convergences speed between Bott′s and nonlinear methods

图6 Bott法与非线性方法的耗时对比Fig.6 Computation of time comparison belotween Bott′s and nonlinear methods

为了对比两种方法单次迭代的计算开销，作者将反演次数设置为1次，并统计了包括初值计算在内的初次迭代时间随界面节点个数的变化(图6)。这里，x与y方向上的节点个数相等。例如，图6中横轴上的数字25表示x和y方向的节点个数均为5，即25=5×5，依此类推。显然，Bott法在计算效率上相对于非线性方法而言具有跨数量级的优势，这是因为在非线性方法的每次迭代过程中都需要求解线性代数方程组，而与之相应的矩阵求逆需要耗费大量时间。与之相比，在利用Bott法进行反演的过程中，模型修正量的计算过程则相当简单，时间主要消耗在模型响应的计算上。

4 结 论

针对重力异常界面深度反演，本文基于合成模型对Bott法和非线性方法展开了详细的对比，并得到以下几点认识：

1)两种方法的反演结果没有明显差异。

2)若单独以迭代次数作为评判标准，则非线性方法的收敛速度要优于Bott法。

3)Bott法在单次迭代耗时和反演计算总时间均远远小于非线性方法。

然而，需要指出的是，尽管Bott法在计算效率上具有优势，但该方法要求重力数据点位与界面节点的水平位置——对应，且位于水平面上。与之相比，非线性反演对数据点的位置则没有特殊要求。在实际勘探中，可根据研究区的客观条件(例如地形起伏幅度)选择合适的方法。