层状介质中大地电磁场信号时域阻抗分析

吴鸿卿，严家斌 ，王 慧，李大雁

(1．中南大学 地球科学与信息物理学院, 湖南 长沙 410083;2．中南大学 有色资源与地质灾害探查湖南省重点实验室，湖南 长沙 410083;3.核工业二三零研究所，湖南 长沙 410007)

1 引 言

大地电磁测深法(MT)自20世纪50年代问世以来，以其工作效率高、装置轻便、勘探深度大、不受高阻层影响等优点而受到人们的关注[1]，在矿产勘查、地下水与地热勘探、油气普查、地壳及岩石圈深部结构探测等领域起着十分重要的作用。由于大地电磁信号源本身的不稳定性、人类活动及其电磁信号干扰和测量系统自身噪声的存在，使得大地电磁信号具有非平稳性、非线形、非最小相位等特性[2]。大地电磁测深方法的数据处理就是一个获得准确阻抗的过程，也是一个不断去噪的过程[3]。Sims提出了最小二乘法估计阻抗方法，该方法在数据噪声满足独立高斯分布规律时，最小二乘法估计为最优无偏估计[4]。当测量的数据存在异常点，在使用最小二乘法进行阻抗估计时，结果往往会产生严重的偏差，研究人员提出了各种形式的Robust阻抗估计法[5]。Egber利用M回归估计降低飞点的权，使其对阻抗函数的估计影响减小[6]。M回归估计仅考虑了电道上存在了噪声，但是磁道上也存在着噪声，汤井田等提出了有界影响估计来解决这一问题[7]。Smirnov在重复中值估计的基础上将其应用到大地电磁阻抗估计中，保证了数据不受异常值和大误差的影响[8]。张刚等将基于重复中位数估计的Robust法应用长周期大地电磁阻抗估算中，取得了较好的效果[9]。对于复杂的海洋环境，常规的阻抗估计方法难以得出可靠的结果，柳建新等提出了根据相关系数的改进Robust阻抗估算方法[10]。Chave等根据数据自身的噪声分布进行加权，提出了基于Stable分布的最大似然估计法，得出了可靠的阻抗估计值[11]。稳健性估计方法是基于对未受干扰或者受干扰较小的数据对异常数据进行降权，但是当异常数据幅度很大或电道与磁道均存在噪声时，就会使得阻抗结果产生偏倚。电道和磁道数据中都存在噪声，Gambal等提出了远参考道阵列观测方法，解决了磁场输入信号受噪声干扰的问题[12]。Larsen等[13]提出了稳健光滑电磁的转换函数，在远参考点存在的条件下，把Robust用到远参考估计中。Lesniak等把Kalman滤波方法应用到大地电磁数据处理中，消除了不相关噪声的影响[14]。汤井田等[15]，蔡剑华等[16]将HHT算法应用到大地电磁信号分析中，短时Fourier变换、Wing-Ville分布和小波变换时频分析方法，HHT方法更具适应性,能更好地揭示电磁场的分布规律[16]。大地电磁信号分析，频率域阻抗估计是基于观测电磁信号的稳定性，而对于非稳定信号,时域比频率域估算阻抗具有更好的稳定性和可靠性。时域上能很好表现出噪声的局部特征,有利于信号的筛选，在时域上估算阻抗能表现出对噪声的不敏感性,阻抗的稳定估算只需短时稳定信号。Yee等[17]用自适应参数时域方法对阻抗张量进行重构，将观测到的MT数据直接用于估计。Spagnolini[18]提出了一种基于实测电场和磁场数据的阻抗张量自适应时域估计方法，自适应估计在时域内最小均方解，使实测数据与模拟数据的均方误差最小，发现时域估计只需要短时间的平稳性。本文从频率域传递函数出发，利用傅里叶变换，将其转化为时间域传递函数，得到时间域下的层状介质视电阻率表达式及时间域测深曲线，比较分析了时域阻抗估计的特点。

2 时域大地电磁测深阻抗估计

水平层状介质时域大地电磁测深表达式是从频率域传递函数出发并对其进行求解，之后利用傅里叶变换，将其转化为时间域传递函数，得到时间域层状介质视电阻率公式。

2.1 时间域电磁场传递函数

时间域中联系电磁场分量的传递函数[19]记为D(t)，定义为：

(1)

式(1)中,*表示褶积;t表示时间，E(t)是时间域电场分量lH(t)是时间域磁场分量。对于D(t)的求解，需要从与其对应的频率域的传递函数出发，其表达式为：

E(ω)=D(ω)·[-iωH(ω)]

(2)

式(2)中,D(ω)为频率域传递函数;ω表示频率;E(ω)频率域电场分量;H(ω)是频率域磁场分量。E(ω)由大地电磁场的阻抗关系可表示为[19]：

(3)

其中,Z(ω)是阻抗，将式(2)和式(3)相比得到：

(4)

其中μ是导磁率;σ1是导电率。式中Rn(ω)[19]为频率域下的N层介质的阻抗函数:

(5)

(6)

利用傅氏变换公式：

(7)

可求出D(ω)的傅氏反变换为：

(8)

ρ1为第一层电阻率，其中

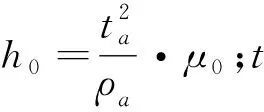
其中

且有

Ln-1=Kn-1,n

图1 一维模型分层后的地层参数Fig.1 Stratigraphic parameter map after layering of one-dimensional model

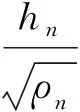
(10)

2.2 时域电阻率估计

由式(8)得到：

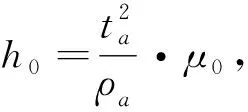
(11)

得到时间域归一化视电阻率为：

ρa=ρ1×S2(t)=4π2tD2(t)

(12)

3 模型分析

建立模型对时间域视电阻率估计的方法进行验证，并分析子层综合参数以及划分的子层数对时域电阻率的影响。

3.1 模型建立与方法验证

给定三层地质模型ρ1=900 Ω·m,ρ2=400 Ω·m,ρ3=900 Ω·m,h1=900 m,h2=600 m,h3=,令各子层的综合参数则对于第一层分为30个子层，每层层厚30 m；第二层分为30个子层，每层厚20 m，如图2所示。分析时间范围10-5～102s，计算得到的时域电阻率如图3所示。从图中可以看到时域曲线与频率曲线一致，首支曲线和尾支曲线与模型的第一层和第三层电阻率相同，证明了该算法的可靠性。

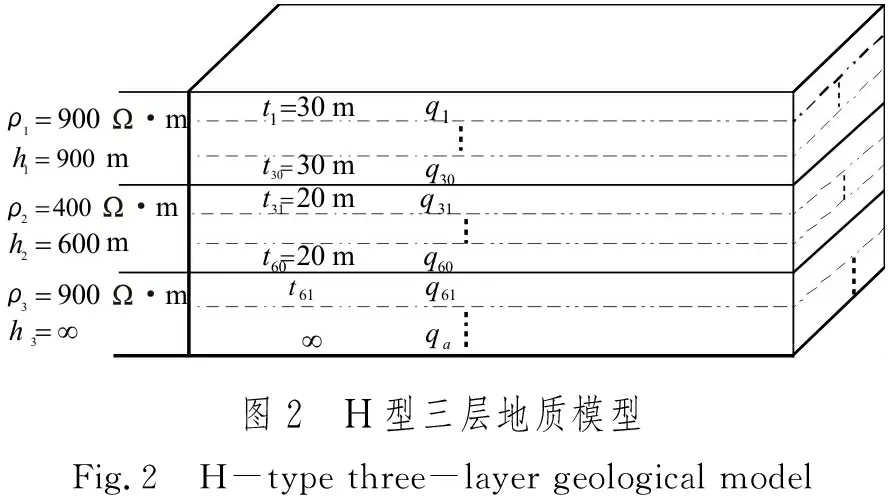
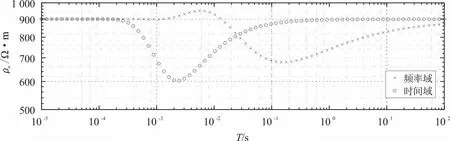
图3 H型三层介质时间域视电阻率曲线Fig.3 H-type three-layer dielectric time domain apparent resistivity curve

3.2 模型分析

3.2.1 二层G型模型

由图4可以看出，当子层综合参数c给定的时候，所取的子层数a不同，所得到的曲线不一样，只要满足a×c=350的条件，所得到视电阻率曲线(图4)接近理论曲线(图5b)。当子层综合参数取1，所取子层数为350时，所得到的视电阻率曲线最接近理论曲线(图4d)。

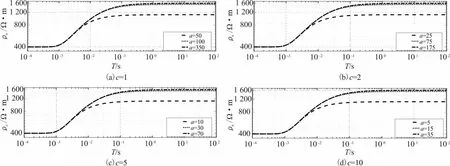
图4 不同子层参数的G型时间域视电阻率曲线Fig.4 G-type time domain apparent resistivity curve of different sublayer parameters注：c为子层综合参数，a为选取的总的层数

图5 不同子层参数的G型时间域视电阻率曲线对比和G型理论曲线Fig.5 Comparison of G-type apparent resistivity curves in time domain with different sub-layer parameters and G-type theoretical curves

3.2.2 三层H型模型

由图6可以看出，在相同的H型模型下，当子层综合参数c给定的时候，所取的子层数a不同，所得到的理论曲线不一样，只要满足a×c=330的条件，所得到视电阻率曲线(图6)就接近理论曲线(图7b)。当子层综合参数取1时，所取子层数为330时，所得到的视电阻率曲线最接近理论曲线(图6d)。

图6 不同子层参数的H型时间域视电阻率曲线Fig.6 H-type time domain apparent resistivity curve of different sublayer parameters

图7 不同子层参数的H型时域视电阻率曲线对比及H型理论曲线Fig.7 Comparison of H-type apparent resistivity curves in time domain with different sub-layer parameters and H-type theoretical curves

4 大地电磁测深曲线的时域与频域比较

4.1 G型曲线

模型参数取ρ1=400 Ω·m，ρ2=900 Ω·m，h1=1 000 m。

由图8可见，频率域和时间域两条曲线在10-3s以前即首支曲线重合，与第一层的电阻率400 Ω·m一致；随着时间的增加或频率的降低，视电阻率逐渐增大，频率域和时间域两条曲线的尾支渐近线，与第二层真实视电阻率相近。时间域曲线在10-3s开始受第二层电阻率的影响，视电阻率开始增大；而频率域曲线要在3×10-3s 才受第二层的影响；同时时间域曲线在1 s时电阻率达到第二层的真电阻，而频率域曲线10 s还没达到第二层的真电阻率，表明时间域电阻率相对于频率域有更大的探测深度；频率域曲线大约在3×10-3～5×10-2s出现了向下凹，出现假的低阻异常，这可能是由于界面反射波和入射波干涉引起的[20,21]，而在时间域曲线中并没有出现。

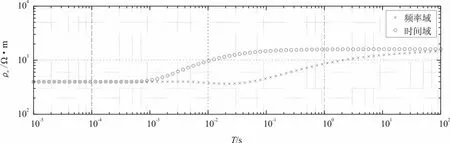
图8 G型二层介质时频域视电阻率对比Fig.8 Comparison of apparent resistivity of frequency domain in G-type two-layer medium

4.2 D型曲线

模型参数取ρ1=1 600 Ω·m，ρ2=400 Ω·m，h1=2 000 m。

由图9可见，频率域和时间域两条曲线在10-3s以前即首支曲线重合，与第一层的电阻率1 600 Ω·m一致；随着时间的增加或频率的降低，视电阻率逐渐减小，频率域和时间域两条曲线的支渐近线，与第二层真实视电阻率相近。时间域曲线在10-3s开始受第二层电阻率的影响，频率域曲线要在3×10-3s才受第二层的影响；同时时间域曲线在10-1s时电阻率达到第二层的真电阻率，而频率域曲线100 s还没达到第二层的真电阻率，表明时间域电阻率相对于频率域有更大的探测深度；频率域曲线大约在3×10-3～8×10-2s时间段出现向上隆起，出现假的低阻异常，同样在时间域曲线中并没有出现。

4.3 H型曲线

模型参数取ρ1=900 Ω·m，ρ2=400 Ω·m，ρ3=900 Ω·m，h1=400 m，h2=600 m。

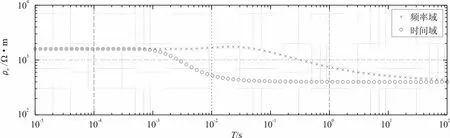
图9 D型二层介质时频域视电阻率对比Fig.9 Comparison of apparent resistivity of frequency domain in D-type two-layer medium

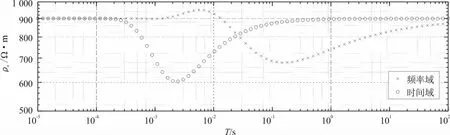
图10 H型三层介质时频域视电阻率对比Fig.10 Comparison of time-frequency domain apparent resistivity of H-type three-layer medium

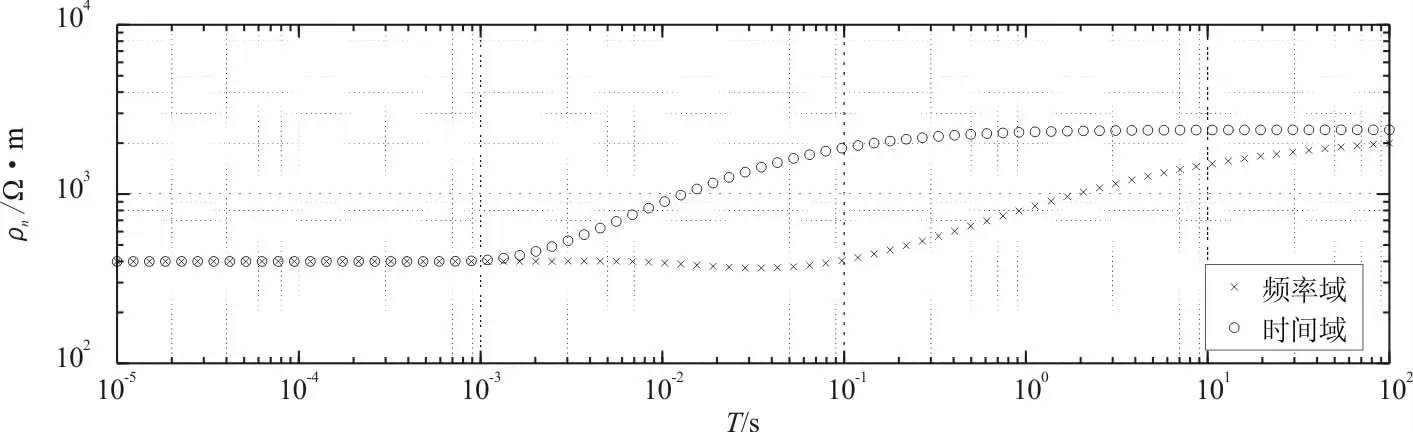
图11 A型三层介质时频域视电阻率对比Fig.11 Comparison of the apparent resistivity of the frequency domain in the A-type three-layer medium

由图10可见，频率域和时间域两条曲线在3×10-4s以前即首支曲线重合，与第一层的电阻率900 Ω·m一致；随着时间的增加或频率的降低，视电阻率逐渐减小，到达一个极小值后，又逐渐增加，频率域和时间域曲线都存在尾支渐近线，与第三层真实视电阻率相近，时间域曲线在3×10-4s开始受第二层电阻率的影响，频率域曲线要在2×10-3s才受第二层的影响；同时时间域曲线在1 s时电阻率达到第三层的真电阻率，而频率域曲线100 s还没达到第三层的真电阻率，表明时间域电阻率相对于频率域有更大的探测深度；时间域曲线在2×10-3s左右达到极大值，而频率域曲线在0.2 s左右才达到极小值且大于时间域曲线的极小值，表明时间域电阻率相对于频率域电阻率更逼近中间层电阻率值；频率域曲线大约在2×10-3～7×10-3s时间段出现向上隆起，出现假的低阻异常，同样在时间域曲线中并没有出现。

4.4 A型曲线

模型参数取ρ1=400 Ω·m，ρ2=1 600 Ω·m，ρ3=2 400 Ω·m，h1=1 200 m，h2=2 400 m。

由图11可知，频率域和时间域两条曲线在10-3s以前即首支曲线重合，与第一层的电阻率400 Ω·m一致；随着时间的增加或频率的降低，视电阻率逐渐增加，频率域和时间域两条曲线都存在尾支渐近线，与第三层真实视电阻率相近，时间域曲线在10-3s开始受第二层电阻率的影响，频率域曲线要10-2s才受第二层的影响；同时时间域曲线在1 s时电阻率达到第二层的真电阻率，而频率域曲线100 s还没达到第二层的真电阻率，表明时间域电阻率相对于频率域有更大的探测深度；频率域曲线大约在10-2～10-1s时间段出现向下凹，出现假的低阻异常，同样在时间域曲线中并没有出现。

4.5 Q型曲线

模型参数取ρ1=1 600 Ω·m，ρ2=900 Ω·m，ρ3=400 Ω·m，h1=2 400 m，h2=1 800 m。

由图12可见，频率域和时间域两条曲线在10-3s以前即首支曲线重合，与第一层的电阻率1 600 Ω·m一致；随着时间的增加或频率的降低，视电阻率逐渐减小，频率域和时间域两条曲线都存在尾支渐近线，与第三层真实视电阻率相近，时间域曲线在10-3s开始受第二层电阻率的影响，频率域曲线要5×10-2s才受第二层的影响；同时时间域曲线在1 s时电阻率达到第二层的真电阻率，而频率域曲线100 s还没达到第二层的真电阻率，表明时间域电阻率相对于频率域有更大的探测深度；频率域曲线大约在5×10-2s～5×10-1s时间段出现向上隆起，出现假的低阻异常，同样在时间域曲线中并没有出现。

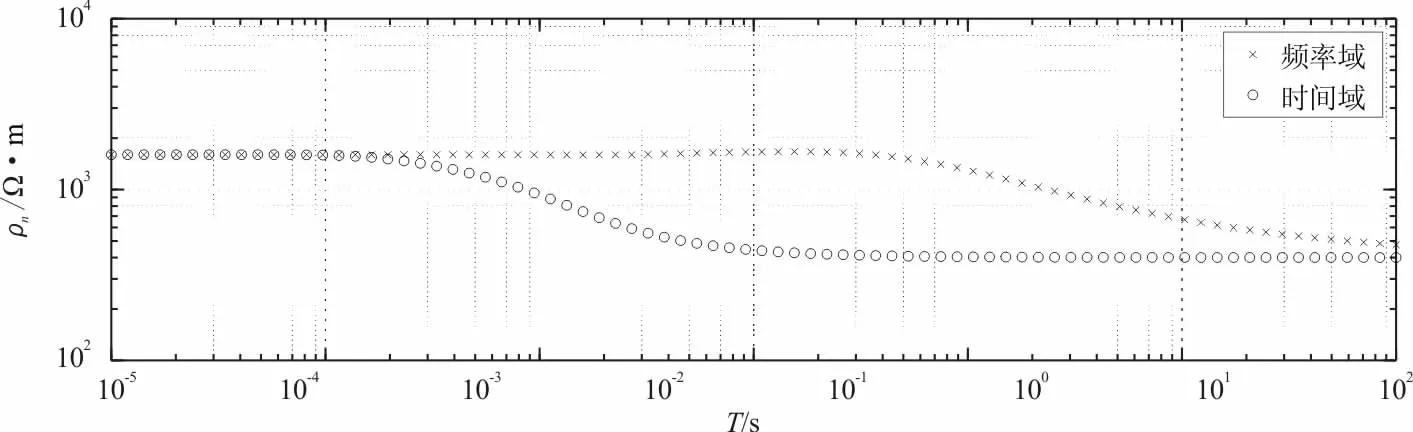
图12 Q型三层介质时频域视电阻率对比Fig.12 Comparison of the apparent resistivity of the Q-type three-layer medium

4.6 K型曲线

模型参数取ρ1=400 Ω·m，ρ2=1 600 Ω·m，ρ3=400 Ω·m，h1=1 200 m，h2=2 400 m。

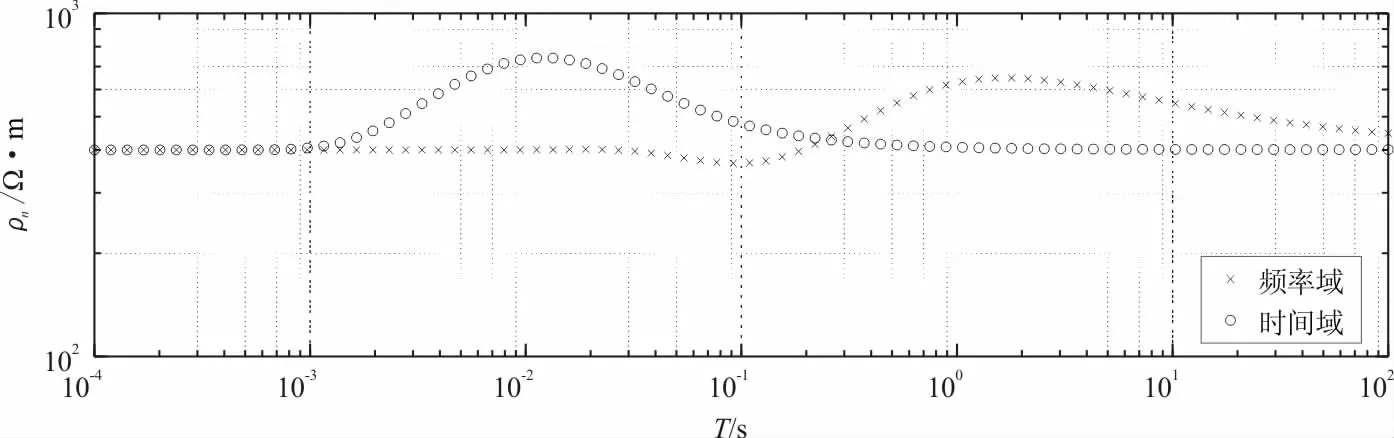
图13 K型三层介质时频域视电阻率对比Fig.13 Comparison of apparent resistivity of frequency domain in K-type three-layer medium

由图13，频率域和时间域两条曲线在10-3s以前即首支曲线重合，与第一层的电阻率400 Ω·m一致；随着时间的增加或频率的降低，视电阻率逐渐增加，到达一个极大值后，又逐渐减小，频率域和时间域两条曲线都存在尾支渐近线，与第三层真实视电阻率相近，时间域曲线在10-3s开始受第二层电阻率的影响，频率域曲线要5×10-2s才受第二层的影响；同时时间域曲线在1 s时电阻率达到第二层的真电阻率，而频率域曲线100 s还没达到第二层的真电阻率，表明时间域电阻率相对于频率域有更大的探测深度；时间域曲线在2×10-2s左右达到极大值，而频率域曲线在2 s左右才达到极大值且小于时间域曲线的极大值，表明时间域电阻率相对于频率域电阻率更逼近中间层电阻率值；频率域曲线大约在5×10-2～5×10-1s时间段出现向下凹，出现假的低阻异常，同样在时间域曲线中并没有出现。

4.7 识别薄层能力的分析

对于三层介质来说，就识别中间薄层电阻率的能力进行分析。通过改变第二层的厚度，将得到的时间域和频率域视电阻率曲线进行分析：

1)模型参数取ρ1=1 600 Ω·m，ρ2=400 Ω·m，ρ3=3 000 Ω·m，h1=1 000 m，h2取1 000 m、500 m、100 m和50 m。

图14中(a)、(b)、(c)、(d)分别是第二层厚度取1 000 m、500 m、100 m和50 m的时频域视电阻率对比图。从图14中可以看出，在中间层厚度为1 000 m和500 m时，时间域曲线中反映的中间层视电阻率值相较于频率域曲线的中间层视电阻率值更接近中间层真电阻率；当中间层厚度为100 m和50 m这样的薄层的时候，频率域曲线中反映的中间层视电阻率值相较于时间域曲线的中间层视电阻率值更接近中间层真电阻率，由此可以得出，时间域视电阻率识别中间薄层的能力可能没有频率域视电阻率的强。

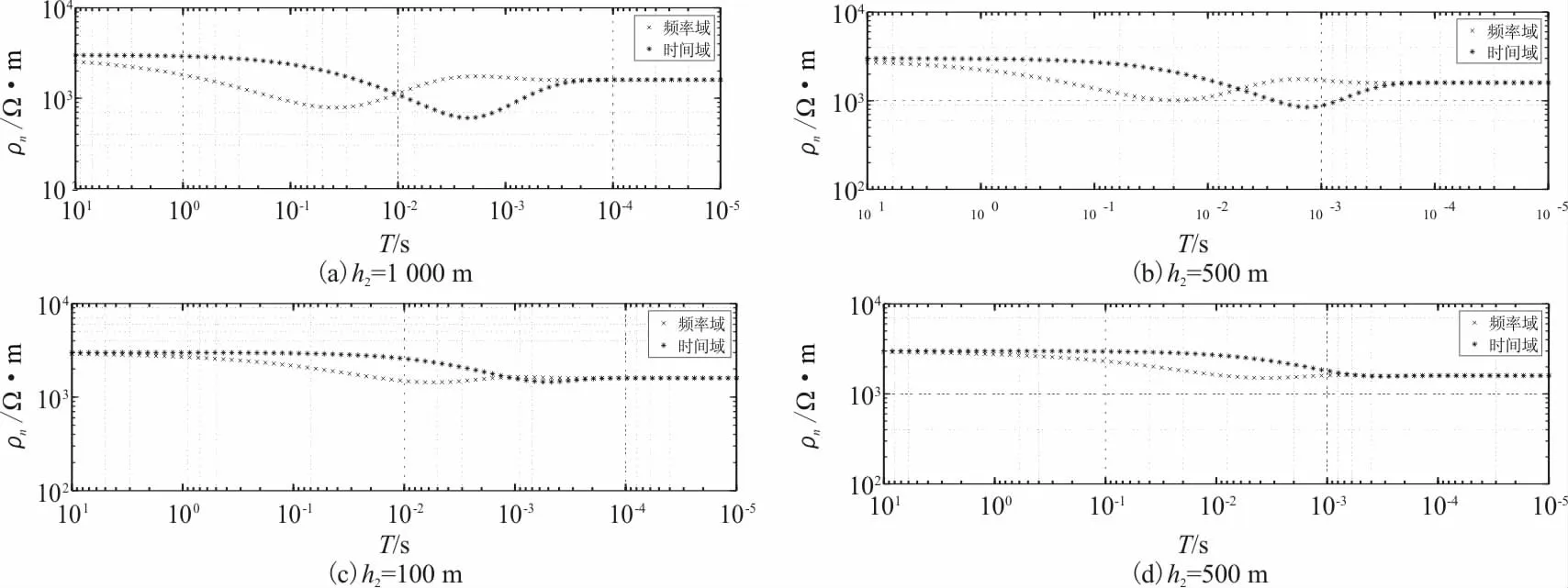
图14 H型三层介质不同中间层厚度的时频域视电阻率对比Fig.14 Comparison of time-frequency domain apparent resistivity of different intermediate layer thicknesses of H-type three-layer medium

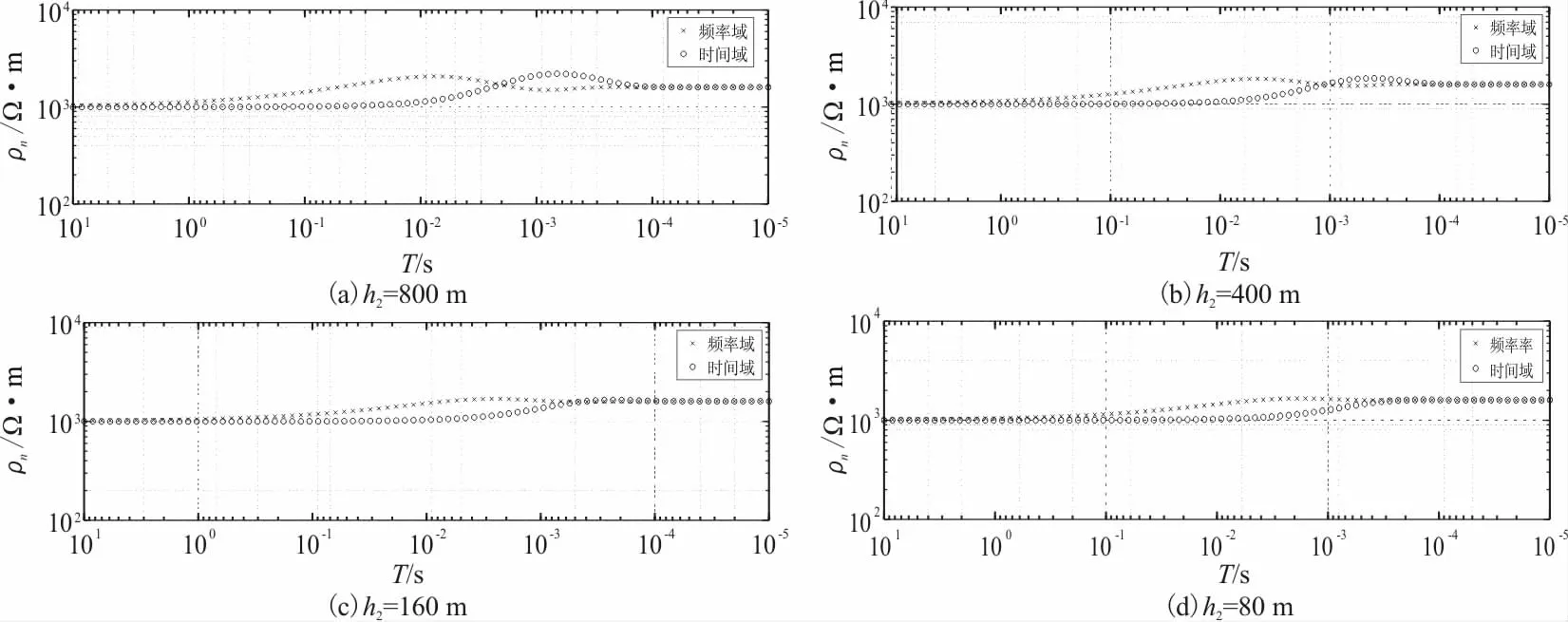
图15 K型三层介质不同中间层厚度的时频域视电阻率对比Fig.15 Comparison of time-frequency domain apparent resistivity of different intermediate layer thicknesses of K-type three-layer medium

2)模型参数取ρ1=1 600 Ω·m ，ρ2=6 400 Ω·m，ρ3=1 000 Ω·m，h1=800 m，h2取800 m、400 m、160 m和80 m。

图15中(a)、(b)、(c)、(d)分别是第二层厚度取800 m、400 m、160 m和80 m的时频域视电阻率对比图。从图5中可以看出，在中间层厚度为800 m和400 m时，时间域曲线中反映的中间层视电阻率值相较于频率域曲线的中间层视电阻率值更接近中间层真电阻率；当中间层厚度为160 m和80 m这样的薄层的时候，频率域曲线中反映的中间层视电阻率值相较于时间域曲线的中间层视电阻率值更接近中间层真电阻率，从中发现时间域视电阻率识别中间薄层的能力可能没有频率域视电阻率的强。

5 结 论

1)通过模型分析表明，在所分层数相同的情况下，子层综合参数越大，即分的层数越多，计算得到的视电阻率越精确。

2)在相同频率下，时间域视电阻率比频率域视电阻率探测深度更大；由于界面反射波和入射波干涉，频率域视电阻率曲线在高频段会出现假异常现象，而时间域视电阻率曲线并未出现；可以看出时间域比频率域估算阻抗或电阻率更准确。

3)通过改变第二层厚度，对所建立的K型和H型三层介质模型进行分析，发现时间域视电阻率识别中间薄层的能力可能没有频率域视电阻率的强。