基于相关移位BOC(n,n)无模糊度捕获算法

孙希延， 郝放， 纪元法， 蔚保国， 郝青儒， 甘兴利， 甄卫民

(1.桂林电子科技大学 广西精密导航技术与应用重点实验室，广西，桂林 541004;2.卫星导航系统与装备技术国家重点实验室，河北，石家庄 050000；3.电波环境特性及模化技术重点实验室，山东，青岛 266000 )

全球卫星导航系统(global navigation satellite system,GNSS)现阶段在各行各业应用十分广泛，它能在全球范围内，全天候、实时地为用户提供高精度导航、定位以及授时等服务[1]. GNSS采用扩频通信体制，因为该体制具有良好的抗干扰特性和良好的保密性等优点. 随着全球经济的发展，GNSS民用服务的需求越来越大，各国都研制了各自的GNSS以抢占这部分市场. 比较典型GNSS包括：美国的GPS(global positioning system)、俄罗斯的GLONASS系统、欧盟的GALILEO系统和中国的BDS (Beidou navigation satellite system)系统. 随着各大卫星导航系统的发展，信号间相互干扰、频段拥挤不堪、信号保密性急剧下降、各系统之间不兼容等问题日益严重. 为解决上述问题，提出了一种新的调制方式：二进制偏移载波(binary offset carrier，BOC)调制，这种调制方式具有更高的码跟踪精度，自相关函数(autocorrelation function，ACF)的主峰更窄以及频谱的分裂特性，很好地解决了现在所面临的问题.

虽然BOC信号有很多的优点，但是其自相关函数的多峰特性使得对捕获跟踪的难度加大. 目前国内外比较突出的研究成果有：①单边带捕获算法[1-4]:这种方法的思想是将BOC信号看成两个BPSK信号的组合，分别对每个BPSK信号进行单独处理再做非相干累加. 这种方法虽然消除了副峰，但是相关峰的宽度失去了BOC信号的优势，跨度为2个码片宽度，而且硬件资源消耗很多. ②SCPC(subcarrier phase cancellation)算法[5]：这种方法的思想是本地产生正弦BOC信号和余弦BOC信号分别与接收信号相关，然后经过算法运算处理，以消除捕获模糊度，但该算法仍存在副峰的影响. ③ASPECT(autocorrelation side-peak cancellation technique)算法[6]：该算法将BOC信号的自相关和与PRN序列的互相关进行平方后再相减，基本上消除了BOC信号自相关副峰，但只适用于BOC(n,n)信号. ④超前滞后互相关组合算法[7]：该算法利用BOC信号与PRN序列的互相关函数分别左右偏移半个码片再进行组合得到无边峰的新函数，消除了模糊性. 其中②③④可以归类为相关重构这一大思路下，相关重构算法也是现今比较热门的研究方向，它的核心思路是[8-18]：通过将有边峰的相关函数拆分，通过算法运算，重新组合构成一个无边峰干扰的新的相关函数.

本文提出了一种新的无模糊度捕获算法，它通过将本地BOC信号以半个子载波宽度为基准等分成两部分，取奇数部分加偶数部分归零构成奇支路信号，同理取偶数部分加奇数部分归零构成偶支路信号，取奇支路信号与接收信号相关，得到的相关函数滞后半个码片取反，得到的新相关函数与原相关函数做相乘运算，取模，再与不取模时的相加，以达到消峰目的(或者取偶支路信号与接收信号相关，得到的相关函数超前半个码片取反，得到的新相关函数与原相关函数做相乘运算，取模，再与不取模时的相加，以达到消峰目的). 经仿真发现，该算法有效消除了相关函数的副峰，同时保持窄带相关峰值，并把主峰跨度减小到半个码片，提高了捕获性能.

1 算法分析

1.1 BOC调制信号捕获存在的问题

自相关函数(ACF)可以通过BOC信号和经副载波调制的PRN序列之间的相关操作获得. BOC(1,1)信号的ACF的模型如下

(1)

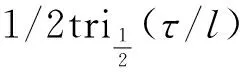
由图中可得，GPS C/A信号自相关函数仅有一个主峰，而BOC(1,1)信号自相关函数主峰跨度是GPS C/A的1/2，使得BOC(1,1)信号有更好的跟踪精度，但其自相关函数有两个副峰，这就让捕获存在误捕情况，如何消除副峰，是要解决的关键问题.

1.2 相关移位边峰消除技术捕获算法

图2显示了BOC(n,n)信号相关移位边峰消除技术(correlation shift side-peak cancellation technique,CSSPeCT)捕获算法的框图. 首先，产生两个正交本地载波，同时剥离接收的中频(IF)BOC(n,n)信号的载波. 然后，经副载波调制的本地PRN序列以副载波脉冲长度作为基准被分割为奇单元部分和偶单元部分，其中奇单元加偶单元归零构成奇支路信号，同理奇单元归零加偶单元构成偶支路信号. 奇支路信号与输入信号相关，产生奇支路相关函数并滞后半个码片长度的采样点数取反，之后新函数与奇支路相关函数相乘，再进行取模，并与不取模的函数相加(或者偶支路信号与输入信号相关，产生偶支路相关函数并超前半个码片长度的采样点数取反，之后新函数与偶支路相关函数相乘，再进行取模，并与不取模的函数相加，以下着重讲解奇支路相关移位方式)，最终ACF的边峰被消除，可以得到清晰的检测变量.

本地伪随机序列可以表示为

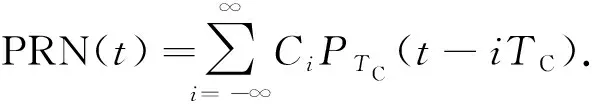
(2)

式中：PTC为周期为TC、振幅为1的矩形脉冲；TC为一个码片的宽度;Ci为码片的符号，Ci∈(-1,1). 本地副载波用数学公式表示为

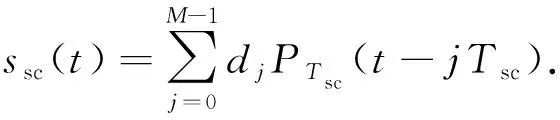
(3)

式中：PTsc为周期为Tsc的矩形脉冲，即一个副载波脉冲的宽度，振幅为1；dj为副载波的脉冲符号;M为一个PRN码片内的脉冲总数. 对于BOC(1,1)信号而言，dj∈(-1,1)，Tsc=Tc/2，M=2.

则本地BOC信号可表示为

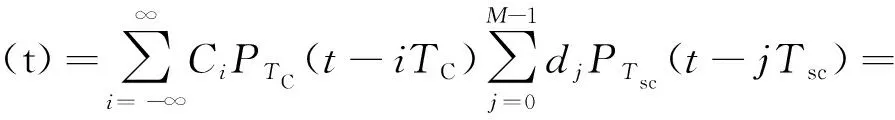
(4)

副载波和本地PRN序列严格同步. 然后，以每个PRN码片长度为基准，按副载波的脉冲持续时间截取成相等的两个部分，前半部分加后半部分归零构奇支路BOC信号，前半部分取0加后半部分构成BOC偶支路信号.CO(t)代表奇支路部分，CE(t)代表偶支路部分. 具体表示如下：

(5)

(6)

式中：Nc为一段时间内PRN码片的数量；dO为以每个PRN码片长度为基准的前半个码片所对应的副载波脉冲符号；dE为以每个PRN码片长度为基准的后半个码片所对应的副载波脉冲符号，且dO&dE∈dj. 图3为本地BOC信号的分离结果图.

而将奇支路滞后取反得

(7)

式中TSC=TC/2，-dO=dE，所以奇支路滞后半个码片取反可得到偶支路信号，同理偶支路信号超前半个码片取反可得奇支路信号.

CE(t)=-CO(t-TC/2),

(8)

CO(t)=-CE(t+TC/2).

(9)

以上得到了本地奇支路信号，接着进行捕获处理，输入BOC信号表示如下：

cos[2π(fIF+fD)t]+n(t).

(10)

式中：PS为输入信号的功率；C(t)为PRN码；D(t)为导航数据；τ为输入信号的码延迟；fD为输入信号的多普勒频率；fIF为中频；SC(t)为副载波；n(t)为噪声项.

输入信号与本地载波混合，然后乘奇支路信号.

SO(t)=S(t){cos[2π(fIF+fD)t]+

jsin[2π(fIF+fD)t]}CO(t)+nO.

(11)

式中CO(t)代表本地奇支路信号，D(t)是一个常数，不影响整体过程，此处省略，无需考虑导航数据位的转换. 再滞后Tc/2取反，可得到滞后取反信号为

SE(t)=-S(t)[cos[2π(fIF+fD)t]+

(12)

再进行相干积分，输出如下：

[cos(πΔfDTs)+sin(πΔfDTs)]+NE.

(13)

[cos(πΔfDTs)+sin(πΔfDTs)]+NO.

(14)

式中：RO(Δτ)为一个奇支路相关函数；RE(Δτ)为移位后的新相关函数；Δτ为码延迟；ΔfD为多普勒频率偏置；NE和NO为遵循高斯分布的白高斯噪音，平均值为0，方差为σ2.RO(Δτ)、RE(Δτ)的数学公式为

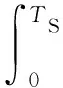
(15)

(16)

图4为两支路相关函数移位图.

(17)

(18)

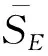
SOE=[SE(Δτ,ΔfD)+NE][SO(Δτ,ΔfD)+NO]=

SE(Δτ,ΔfD)SO(Δτ,ΔfD)+SE(Δτ,ΔfD)×

NO+SO(Δτ,ΔfD)NE+NENO.

(19)

最后根据提出的算法实现无模糊度的捕获，其中V为最终检测量

V=|SOE|+SOE.

(20)

1.3 Matlab仿真结果

基于Matlab平台，设输入信号中频为4.092 MHz，取采样率为40.92 MHz，设置码相位偏移为第601个采样点，多普勒为1 100 Hz，信噪比为-19 dB，利用相关移位边峰消除技术对BOC(1,1)信号捕获的结果如图5所示.SOE,|SOE|以及根据式(20)重建的相关函数V如图6所示.

如图6所示，SOE存在两个负的边峰，边峰与码相位τ=601对称. |SOE|存在两个正的边峰与SOE的两个边峰位于同一码相位. 将SOE加上|SOE|可以得到清晰的相关峰，即V.

2 性能分析

基于Matlab平台，设置同2.3节，将CSSPeCT、CSSPeCT取模相加之前的方法(即只进行移位相乘)、ASPeCT和BPSK-LIKE 4种捕获方法进行对比，以比较性能的优劣性.

2.1 捕获结果二维对比仿真

图7为4种方法的捕获二维对比图. 可以直观地看出CSSPeCT方法明显优于CSSPeCT取模相加之前、ASPeCT和BPSK-LIKE方法. 在主峰跨度方面，CSSPeCT方法主峰跨度为20个采样点(半个码片宽度)同其取模相加之前的方法和ASPeCT方法，并且优于BPSK-LIKE方法(80个采样点，即2个码片宽度)；而峰值方面也明显同CSSPeCT取模相加之前的方法和ASPeCT方法，且高于BPSK-LIKE方法10%. 与CSSPeCT取模相加之前的方法和ASPeCT方法不同点在于CSSPeCT方法完全消除了副峰的影响，而ASPeCT方法和CSSPeCT取模相加之前的方法仍有两个较小的副峰. 值得注意的是CSSPeCT取模相加之前的方法与ASPeCT方法最终函数基本相同.

2.2 检测概率对比仿真

检测概率对比图，是衡量一种捕获方法优劣的最好方式，图8为4种方法的检测概率对比图，捕获判定的依据为不同信噪比下最大值出现的位置与伪码偏移位置的误差在正负1/4个码片内[16].

从图中可以看出，检测概率与ASPeCT方法基本相同，优于BPSK-LIKE方法1 dB左右,且优于CSSPeCT取模相加之前的方法0.5 dB左右.

2.3 峰均比对比仿真

在检测性能上，峰均比也是一种衡量捕获性能好坏的可行方式，即捕获到的最大峰值与均值的比值. 如图9所示，CSSPeCT方法的峰均比在信噪比大于8 dB情况下,明显高于其取模相加之前的方法、ASPeCT方法和BPSK-LIKE方法25%、10%和200%，这大大提高了捕获性能.

2.4 算法运算量分析

以2.3节中设置的参数为例，FFT并行码相位捕获频率间隔为500 Hz，频率范围为: ±10 kHz;FFT并行码相位捕获采用并行码相位搜索的方式进行捕获. 一般而言需要2次FFT运算，1次IFFT运算，也就是说总共需要3次FFT运算量. 而完成一次40 920点FFT的需要复数加法运算次数.

NlbN=40 920lb 40 920=626 916，

需要复数乘法运算：

通常，一次复数乘法可分解为4次实数乘法和3次实数加法，一次复数加法分解为两次实数加法.

本文提出的相关移位边峰消除技术捕获算法经过2次复数乘法运算、1次实数乘法运算和1次实数加法运算，再经过5次FFT得到检测量. ASPeCT方法需要经过4次复数乘法和2次实数加法运算，再经过8次FFT得到检测量. BPSK-Like方法需要8次FFT运算，4次复数乘法和2次实数加法得到检测量. 此处进行一个频点的对比，所有频点对比只需在以下结果中乘以[(10 000×2)/500]+1即可，不影响对比结果. 假设一次乘法和一次加法持续同样时间，可以看出，新算法共进行9 121 125次加法运算和13 030 179次实数乘法运算. BPSK-Like方法的总计算量为53 426 877次，实数乘法为21 370 757次，以及实数加法32 056 120次. ASPeCT方法共进行32 056 120次加法运算和21 370 757次乘法运算. 所以本文提出的方法的计算量是ASPeCT方法和BPSK-Like方法的62%. 图10为ASPeCT方法原理框图，图11为BPSK-Like方法原理框图.

3 结 论

在以快速捕获为前提下，采用并行码相位捕获方法以提高系统速度，提出了一种相关移位边峰消除技术消除BOC(n,n)信号自相关函数的边峰，结果表明在快速捕获的过程中能完全消除边峰，同时保留主峰的窄相关性. 本文通过对捕获二维图、检测概率、峰均比及计算量进行性能分析，表明较ASPeCT和BPSK-LIKE两种传统捕获方法而言，提出的CSSPeCT方法计算量更少，捕获的性能更佳，对于接收我国北斗三代导航系统中的B1C信号很有借鉴意义.