非平稳噪声环境下LFMCW信号恒虚警检测算法研究

苏宇， 蒋德富

(河海大学 计算机与信息学院，江苏,南京 213022)

线性调频连续波(linear frequency modulation continuous wave, LFMCW)雷达具有体积小、成本低、精度高、无距离盲区、低截获(low probability of intercept, LPI)等优点，已广泛应用于军用导航、战场侦查监视、成像等系统中[1-3]. LFMCW雷达的波形具有时宽积大、峰值功率低等特点，给电子侦查中非合作检测带来了巨大的困难. 因此，在低信噪比(signal to noise ratio，SNR)下，研究对LFMCW波形进行可靠的恒虚警率(constant false alarm rate, CFAR)检测，具有重要的现实意义.

文献[4-8]中采用周期Wigner-Ville Hough变换(periodic Wigner-Ville Hough transform，PWVHT)、周期Choi-Williams Hough变换(periodic Choi-Williams Hough transform，PCWHT)、周期分数阶傅里叶变换 (periodic fractional Fourier transform，PFRFT)、Radon-Ambiguity变换(Radon-Ambiguity transform，RAT) 、短时傅里叶变换(short time Fourier transform， STFT)的方法，从参数估计的角度对LFMCW信号进行分析，在时频聚焦性[4-6]、减少计算量[7-8]、抗噪声方面具有优良的性能. 参数估计的前提是有效的信号检测，然而，这些方法未能对检测模型进行分析，以对低信噪比情况下的截获信号进行可靠的CFAR检测. 陈旭敏等[9]采用蒙特卡洛(Monte-Carlo)实验的方法，对Wigner-Ville Hough变换(Wigner-Ville Hough transform，WVHT)、PWVHT、累积WVHT(Cumulative WVHT，CWVHT)算法中时频域虚警门限进行设定，没有对随机信号的分布特性进行分析，检测性能并不可靠. 王泽众等[10-11]分别对随机信号经过周期Wigner-Hough变换(periodic Wigner-Hough transform，PWHT)、PFRFT算法处理后的分布特性进行分析，得到符合卡方分布的信号模型，由卡方分布的概率密度函数(probability density function，PDF)进行固定虚警率下的检测门限的设定. 王杰等[12]分析了随机信号经过单窗口加权并进行离散傅里叶变换(discrete Fourier transform, DFT)后频域信号的分布特性，得出频域包络呈Rayleigh分布的结论，根据Rayleigh分布的PDF设定频域CFAR门限. 上述算法[9-12]虽然能对低SNR的LFMCW信号进行CFAR检测，但是算法实施的前提是对噪声功率进行可靠的统计，然而在复杂的电磁环境中，统计出的噪声功率可能是不准确的，甚至是错误的，而且在截获过程中噪声功率可能是变化的，非平稳的，这些因素都极大地限制着上述检测算法的应用范围.

本文在Thomson多正交窗谐波分析方法的基础上[13]，提出一种对截获的LFMCW信号进行分段多正交窗口加权的检测算法. 采用离散长球序列(discrete prolate spheroidal sequences，DPSS)对信号进行加权离散时间傅里叶变换(DTFT)处理，通过合理的假设和一系列复杂的变换，得出与噪声功率无关的CFAR检测模型. 该算法是在短时傅里叶变换(short time Fourier transform, STFT)的基础上提出的，传统的STFT方法采用单个窗加权，本文采用多个正交窗对序列进行加权，增加了一维自由度，从而便于推导出与噪声无关的CFAR检测模型. 与传统算法[9-12]相比，该算法优点在于：

① 传统算法需要假定噪声在截获过程中符合平稳高斯分布，这在复杂电磁环境中往往很难满足，本文所采用的算法只需假定噪声在时间窗内符合平稳高斯分布，具有更普遍的适用性；

② 本算法中，门限值的设定只与窗的个数和虚警概率有关，与噪声功率无关，因此无需对噪声功率进行统计，避免了统计误差导致的虚警率变化，增加了算法的适用性和可靠性；

③ 采用了离散长球序列，也叫Slepian序列，对信号进行加权. Slepian序列加权是一种使得主瓣能量占总能量最大化的加权技术，信号能量更加集中于主瓣，因此可以提高估计算法的稳定性[14].

1 LFMCW信号截获模型

为了获得信号的幅度和相位信息，截获接收机通常采用模拟正交下变频或者数字正交下变频的技术[15]，将截获信号由实数转换成复数信号，因此本文采用复数模型对截获信号进行建模和分析处理. LFMCW信号的形式主要有两种，即锯齿波信号和三角波信号，为了便于分析，本文采用锯齿波线性调频连续波(sawtooth LFMCW，SLFMCW)信号. 雷达侦查接收机截获的SLFMCW信号可以表示为

ω(n)=x(n)+ω(n).

(1)

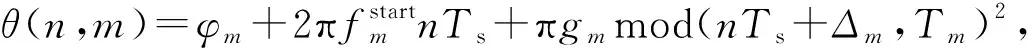
2 频域恒虚警检测

本文采用假设检验的方法对信号进行分析，并说明了如何通过设定检测门限V来控制虚警概率PFA，这里的虚警是指在窗内对某个信号参数的错误检测. 将式(1)表示的截获信号等分成多个时间序列，在时间序列μk内构建二元假设检验：

H0:rn,k=ωn,k,

H1:rn,k=xn,k+ωn,k.

(2)

式中：rn,k表示第k时间序列中第n采样点的值；xn,k为信号项；ωn,k为误差项. 这里第k时间序列可表示为

μk={n:(k-1)N≤n≤kN}.

(3)

文献[16]通过构造时间序列μk内单个LFMCW信号的模型，以μk内最小频谱偏移为准则得出结论：当Tobs≫NTs时，可以设定N的最大值为

(4)

根据上述近似平稳的设定，在时间序列μk内可把信号xn,k近似看成一系列谐波信号的和，建立如下短时谐波模型(short time harmonic model，STHM)：

(5)

式中：Lk≤M表示第k时间序列里截获信号的个数；Ac,k，fc,k分别表示第k时间序列里第c个信号的幅度和载频.

在纽曼-皮尔逊准则下，定义时间窗μk内虚警概率PFA和检测概率PD分别为

(6)

式中：Pr{A|B}为条件概率，指在事件B已经发生的条件下，事件A发生的概率.

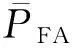
(7)

在仿真中，虚警概率与检测概率皆采用平均虚警概率和平均检测概率表示.

基于上述μk内STHM的建立，在下文中，先给出单个窗加权算法下PFA与门限V的关系，然后对多正交窗加权下的信号进行分析，并推导出其对应的CFAR模型.

2.1 单窗口检测

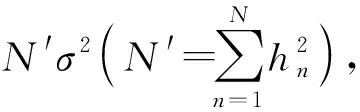
(8)

式中：V1为检测门限；PFA为虚警概率.

由上述分析可知，单窗口方法是采用单个窗函数对信号进行加权DTFT处理，频域CFAR门限的设定与窗宽度N、噪声功率σ2及虚警概率PFA有关. 因此在实际工程中，在信号到来之前，需要对σ2进行估计，而且需要假定在信号观测时间Tobs内，噪声是平稳高斯分布的. 在复杂电磁环境中，对于LFMCW信号，这种条件很难满足，且CFAR检测的前提是σ2的准确估计，任何误差都可能导致虚警率的变化.

2.2 多窗口检测

为了解决上述单窗口算法不适用于复杂电磁环境中对LFMCW信号进行CFAR检测的问题，在本节中，采用多窗口谐波分析的方法对信号进行分析. 基于式(5)中STHM模型，推导出与噪声功率σ2无关的CFAR检测算法，该算法的推导可分为如下几个步骤.

步骤1 采用Slepian窗加权DTFT.

为了便于分析，假设在时间序列μk内只有一个单频信号f1,k存在的情况，模型如下：

rn,k=A1,kej2πf1,knTs+ωn,k.

(9)

利用Slepian窗对上式进行加权求DTFT:

(10)

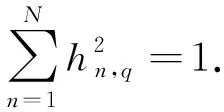
了部分Slepian窗的时域和频域形状，其中N=64，W=5/N，Q≤9. 由图中可以看出，第0和第1个窗函数主瓣能量较为集中，第8个窗函数能量比较分散. 在实际应用中，设计Slepian窗函数步骤如下：

① 确定窗宽度N；

② 确定窗分辨率带宽W；

③ 由N和W确定Q的最大值，调用Matlab指令h=dpss(N,NW,Q)产生Q个Slepian窗，h为N×Q的矩阵，hn,q为矩阵的系数. 特别地，当Q=1时，产生单个Slepian窗，其性能将在后文中分析.

步骤2 建立线性统计模型估计幅度A1,k.

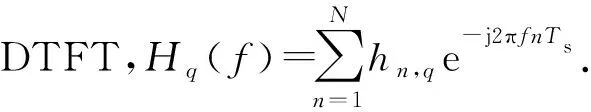
(11)

将式(11)带入式(10)可以得到

(12)

当f=f1,k时，式(12)可写为

(13)

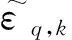
(14)

(15)

步骤3 建立分布函数并推导出CFAR模型.

文献[19]对式(13)中线性模型进行了详细的分析，得出了以下性质.

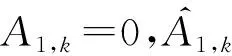
(16)

(17)

即Dk(f1,k)服从自由度为2,2Q-2的F分布. 结合式(6)可得

PFA=Pr{Dk(f1,k)>V2|H0}=

(18)

结合F分布的概率密度函数可以得到门限与虚警概率的关系[17]为

(19)

与式(8)相比，式(19)中门限V2的大小只与窗个数Q以及虚警概率有关，与噪声功率无关，因此无需对噪声功率进行统计分析.

3 仿真结果及分析

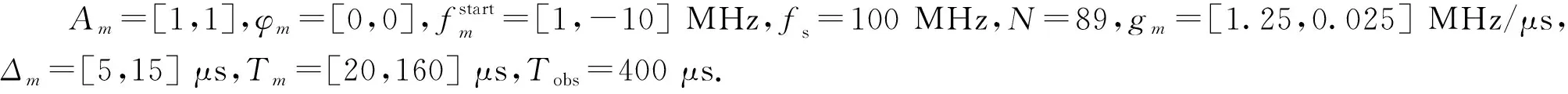
k=1,2,…,K.

(20)

设定非平稳噪声功率变化规律如下：

(21)

式中,α>0为噪声功率变化增益. 在下面的实验中，设定信噪比为信号功率与σ2的比值.

图3为本算法在非平稳噪声状态下检测概率的信噪比曲线. 由图3(a)可得单个SLFMCW 信号的检测性能优于多个SLFMCW信号；低调频斜率的信号的检测性能优于高调频斜率的信号. 因为对于固定的窗长N，由于分辨率2W的限制，多个信号之间会相互干扰，影响载波频率的测量；相对于高调频斜率信号，低调频斜率产生更小的频谱偏移，因此具有更好的检测性能. 分析图3(b)可知：通过增加窗的个数可以提高检测概率，但是窗个数Q的变大，会增加运算量，降低分辨率，因此在实际工程中，需要在计算量和检测性能之间做出取舍，以取得满足需求的检测性能. 图3(c)分析了不同虚警率下检测概率与α的关系，可以看出，在信号截获过程中，本文所提算法的检测性能可以实时跟踪信噪比的变化，当信噪比增大时，检测性能可以实时的提高. 图3(d)分析了不同分辨率带宽下检测概率与窗宽度的变化关系. 由图示可得，窗长度在112左右的时候检测性能最优. 窗长过小，DTFT积累点数少，SNR增益不够，检测性能不高；窗长过大，频谱扩散大，同样会降低检测性能. 在实际工程中，窗长度需要根据检测对象的假定最大斜率设置. 对于相同的窗长度，分辨率带宽越大，对应的窗个数越多，检测性能越好.

图4将本文所提算法与单窗口算法在时域非平稳噪声情况下检测性能进行比较，实验中设定虚警概率为10-3，Q=29，M=1，单窗口窗函数选择矩形窗、Hamming窗和Kaiser窗，其中凯撒窗的分辨率带宽与本文所采用的Slepian窗相同. 图4(a)采用Monte Carlo实验的方法，分析虚警概率随α变化的规律.α从0开始，以0.1为步长递增至5，每个α值做200次实验. 可以看出，本文提出多窗口检测算法在不同α下仍能保持稳定的虚警概率，而单窗口算法的虚警概率随着α的增大而增大. 该实验表明了在信号截获过程中，即使噪声功率谱随时间变化而变化，本文所提算法仍能做到恒虚警率，而传统单窗口算法无法做到这一点. 图4(b)分析了多个Slepian窗与单个窗检测性能随信噪比变化的关系，其中Slepian窗与凯撒窗函数的分辨率相同. 由图示可知，单个Slepian窗检测性能略高于凯撒窗，随着窗个数的增加，本文所提出的多窗口算法的检测性能也随之提高，在低SNR下，性能差异尤其明显.

图5为本算法在高斯色噪声背景下与传统单窗口算法性能对比. 高斯色噪声的特点是噪声功率谱密度在频域非平稳，通常由外部强干扰源产生，通过接收机带通滤波后成为相关的高斯噪声. 图5(a)采用Monte Carlo实验的方法分析了不同窗函数虚警概率与设定值之间的差异. 实验中，设定两种滤波器带宽，为2,40 MHz，分布对应于实际应用中的窄带瞄准式干扰和宽带阻塞式干扰，滤波器通带波动0.001 dB，阻带衰减60 dB. 由于包括本文所提出的算法在内的频域CFAR检测算法皆要求噪声是非相关的，因此无法实现在色噪声背景下CFAR检测. 图中窗口1代表带宽设置为2 MHz，窗口2代表带宽设置为40 MHz. 由图示可以看出，随着干扰噪声带宽的增加，在短时窗内噪声之间的相关性减弱，因此虚警概率逐渐接近设定值，且本文所提出的算法相对于单窗口的算法的虚警概率总体上更加接近设定值. 图5(b)为不同信噪比下，多正交窗与单窗加权方法检测概率的对比，此时的信噪比定义为信号功率与滤波之前的噪声功率之比，滤波带宽设置为20 MHz，虚警概率设置为10-4. 由图中可以看出，对于窄带干扰噪声，即使噪声功率很高，本文所提出的算法检测概率仍然很大；对于宽带干扰噪声，检测概率随着干扰带宽的增加而减小，但是仍然高于传统单窗口算法. 因此可以得出结论，本文所提出的算法在色噪声背景下，性能仍然优于传统的单窗口加权算法.

图6将本文所提出的算法与单窗口算法在参数估计上进行对比，单窗口选择凯撒窗以及单个Slepian窗，以在相同的分辨率条件下进行对比. 图5(a)为采用本文所提算法与单个Slepian以及凯撒窗对任一时间段μk进行加权FFT的结果图，由图可以看出单个Slepian窗的性能与凯撒窗相似，主瓣略窄，第一旁瓣略高. 随着窗个数的增加，Slepian窗加权后的频谱主瓣变窄，旁瓣降低，能聚集性随之提高，因此频率估计结果更加稳定. 3种窗函数在不同信噪比下对不同时间段上频率估计方差的平均值如图5(b)所示，由图可以看出单个Slepian窗参数估计方差略低于凯撒窗，而本文所提出的多正交窗加权的方法估计方差明显小于二者，在参数估计上比单个窗函数性能更优，且性能可以随着窗个数的增加进一步提高.

4 结 论

本文针对LFMCW信号的截获，提出了一种分段多正交窗加权的算法，并推导出与噪声功率无关的CFAR模型. 相对于传统采用单个窗加权的算法，本文所提算法在检测概率、能量聚集性、和频率估计方面具有更优的性能，且算法性能可以随着窗个数的增加而提高. 后续工作需要在此基础上研究LFMCW信号的参数估计、分选、识别以及实时计算等问题.