频率分集阵列雷达波束的相位方向图特性
葛佳昂, 谢军伟, 张浩为, 冯晓宇, 张晶
(1.空军工程大学 防空反导学院,陕西,西安 710051; 2.陕西交通职业技术学院,陕西,西安 710018)
2006年,伦敦大学博士生Paul Antonik在国际雷达会议上首次提出了频率分集阵列(frequency diversity array,FDA)的概念[1],引起了国内外学者广泛关注. 与传统相控阵雷达不同,通过在各阵元之间引入频率增量,FDA雷达阵列发射方向图,即幅度方向图具有角度-距离的二维依赖性,空间波束指向会随距离变化而发生变化,相对于相控阵增加了距离的自由度. 针对频率分集阵列发射方向图特性,文献[2—7]中指出了FDA发射方向图随距离、时间、角度的周期变化规律,并给出了详细的理论推导.
利用FDA波束的距离—角度二维特性,很多学者进行了一系列研究. 文献[8]中分析表明FDA在多径干扰抑制方面优势明显. 文献[9—10]中证明利用FDA波束的距离依赖特性,能够对距离杂波抑制产生更好效果. 许京伟[11]利用FDA-MIMO发射-接收空间角频率的相对关系进行欺骗干扰鉴别,取得了较好效果. 王文钦等[12-15]发表了多篇关于频率分集阵列的综述性文章,对频率分集阵列的研究现状进行了系统总结,并分析了FDA在射频隐身雷达中应用前景.
然而,解决雷达隐身问题,要解决FDA的实现角度欺骗问题. FDA由于其发射方向图与距离相关,发射方向图出现了弯曲现象,因而产生了关于虚拟辐射源的问题,以达到角度欺骗的目的[16-17]. 利用发射方向图的弯曲现象,文献[17]研究了对幅度法测向的角度欺骗. 但是,实现角度欺骗问题,不应只考虑对于幅度法测向的角度欺骗,还应考虑对于相位法测向的角度欺骗. 以干涉仪为代表的相位法测向作为一种无源测向方法,具有测向隐蔽性好、方位测量准确等优点,在侦察系统中应用越来越广泛. 但是,对于该系统的主动对抗还在研究,目前提出了相干干扰的主动对抗方法[18-19]. 考虑FDA对于相位法测向的角度欺骗,就要求对其在空间中相位分布有熟悉的了解. 但是,自2006年提出频率分集阵列雷达概念时,Atonik等[1]就仅给出了频率分级阵列雷达的幅度方向图与传统相控阵雷达的幅度方向图的不同,而没有考虑其在空间中的相位分布. 之后学者的研究也仅对FDA发射方向图进行了详细解释说明而没有研究相位方向图特性[11,16],因此,为了补充对于基本原理的研究,并考虑其应用价值,研究相位方向图具有较大的意义.
本文从FDA波束相位模型出发,利用FDA发射方向图基本建模方法[16]和欧拉公式法分别建立了两种研究FDA波束相位分布的模型,利用仿真分析了两种方法的差距,选择了最优模型,并以此模型建立了FDA相位方向图,利用仿真分析了FDA相位在等高线、等角度线以及等距线的分布特点,并确定了FDA相位分布的同相波前,即等相位面. 经仿真分析,确定了FDA相位分布特性.
1 FDA波束相位模型建立
研究FDA相位方向图时,与传统幅度方向图不同,幅度方向图考虑的波束的指向,而相位方向图研究的是波束相位在空间的分布情况. 因而有必要先对FDA的波束模型的建立,并根据建立的波束模型求取FDA的波束在信号空间的相位,由此确定出FDA波束的相位方向图.
1.1 模型建立法
均匀线性频率分集阵列结构如图1所示.
各阵元发射信号可表示为
sm(t)=exp(j2πfmt),m=0,1,…,N-1.
(1)
其中,各阵元频率为
fm=f0+(m-1)Δf,m=1,2,…,N.
(2)
式中f0、Δf、N分别表示载频,频差和阵元总数. 设空间中某位置{R,θ}处有一远场点目标,阵元m的发射信号,到达远场点目标的信号可表示为
sm(t)=exp[j2πfm(t-rm/c)].
(3)
式中:rm=R0-mdsinθ;d为阵元间距.
在{R,θ}处产生的远场阵列因子为
(4)
由于满足3个条件:①电磁波的远场传播时间远大于相邻阵元波程差传播时间;②远场距离远大于相邻波程差;③中心频率远大于步进频率增量,即
t≫ndsinθ/c,R0≫ndsinθ,f0≫Δf,Rn≈R0.
(5)
因此,j2πn2Δfdsinθ/c的值远小于其他3项,可以忽略不计. 故
AF(t;R0,θ)=
(6)
令Υ=2πf0dsinθ/c+j2πΔf(t-R/c),则
(7)
则
(8)
1.2 欧拉公式法
FDA阵列目标探测示意图,如图2所示.
包含N个阵元的FDA阵列对目标进行照射时,可等效为N个点源对目标进行独立探测的合成. 设第i个点源在目标处的电场强度为
(9)
式中:Emi和φ0i分别表示信号的幅值和初始相位. 则N个点源在目标处合成的电场强度为
(10)
又由欧拉公式ejx=cosx+jsinx及其逆用可得
(11)
其中:
(12)
则
(13)
1.3 模型对比分析
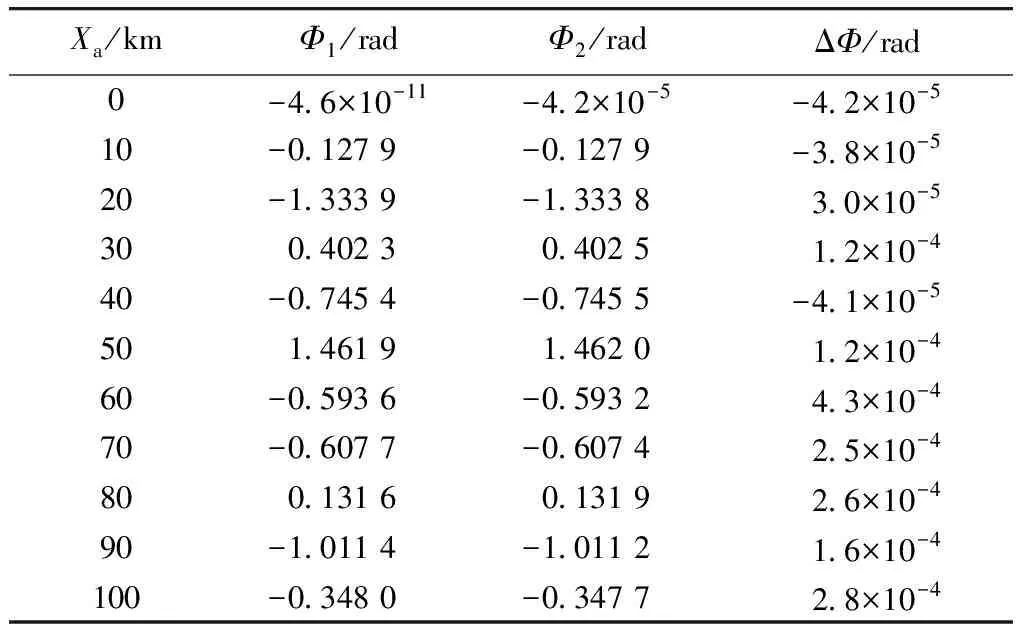
取FDA初始频率f0为1 GHz,阵元间距d为0.15 m,频率增量Δf为1 kHz,阵元数N为5,时间t为0,目标距离FDA阵元初始点的y轴距离Ya为40 km,以目标距离FDA阵元初始点的x轴距离Xa为变量,分别求取利用两种模型求得的相位大小以及两种模型的相位差,如表1所示.
表1 两种模型下FDA波束相位分布对比
Tab.1 Contrast of FDA beam phase distribution under two models
Xa/kmΦ1/radΦ2/radΔΦ/rad0-4.6×10-11-4.2×10-5-4.2×10-510-0.127 9-0.127 9-3.8×10-520-1.333 9-1.333 83.0×10-5300.402 30.402 51.2×10-440-0.745 4-0.745 5-4.1×10-5501.461 91.462 01.2×10-460-0.593 6-0.593 24.3×10-470-0.607 7-0.607 42.5×10-4800.131 60.131 92.6×10-490-1.011 4-1.011 21.6×10-4100-0.348 0-0.347 72.8×10-4
Φ1为利用模型建立法建立模型的相位、Φ2为利用欧拉公式法建立模型的相位,在相同距离上两种方法会具有相位差ΔΦ,下面分析ΔΦ产生原因.
①所采用的模型建立法是在式(5)近似化简得,且其考虑的是远场目标,即不同阵元到目标的波束认为平行,每个阵元到目标的距离并非其真实距离.②利用欧拉公式法直接对阵元发射信号电场强度进行合成,而没有进行近似化简,且其考虑的是每个阵元到目标的真实距离. 所以,欧拉公式法相比于模型建立法减少了近似化简产生的误差.
2 FDA相位方向图建立
由分析可知,利用欧拉公式法求得的条件,相对的误差较小,与实际环境更相符,故仿真采用了欧拉公式法. 下面以欧拉公式法建立的模型,进行相位方向图的建立.
取FDA初始频率f0为1 GHz,阵元间距d为0.15 m,阵元数N为5,时间t为0,以目标距离FDA阵元初始点的x轴距离Xa为40 km,目标距离FDA阵元初始点的y轴距离Ya为变量、分别求取频率增量Δf为0、1 kHz时的相位方向图如图3、图4所示.
由图3和图4可以看出,FDA的相位方向图并不会发生“弯曲”现象,这与FDA的幅度方向图特点并不一致,说明FDA相位变化与传统相控阵相位变化规律相似,传统相控阵的相位规律在FDA相位变化上仍然适用.
3 仿真分析
3.1 等高度不等距的不同目标的相位分布
取FDA初始频率f0为1 GHz,阵元间距d为0.15 m,阵元数N为5,时间t为0,目标距离FDA阵元初始点的y轴距离Ya为50 km,频率增量Δf分别为0、1 kHz,取目标距离FDA阵元初始点的x轴距离Xa为变量,分别求取传统相控阵和FDA的相位分布. 仿真结果如图5所示.
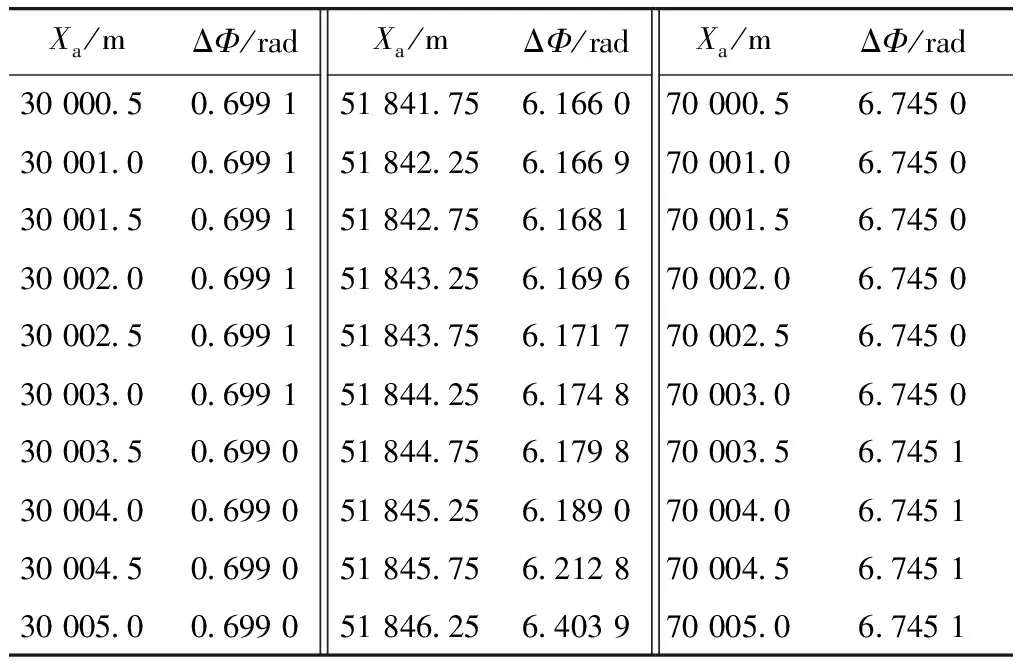
由不同Xa下相控阵和FDA相位变化图形可以看出,FDA相位变化与相控阵相位变化趋势基本一致;但是,由式(13)可知,FDA相位与相控阵相位相比每一项均都多出了fRi/c项的影响,会导致FDA相位超前相控阵相位,因而得到不同Xa下相位差ΔΦ的变化数据如表2所示,由表中数据可以看出,当Xa变化时达到51 846 m左右时,FDA相位会超前相控阵相位2π,即一个周期.
表2 等高度不同距离上相控阵与FDA的相位差
Tab.2 Phase difference of phased array and FDA at equal height at different distances
Xa/mΔΦ/radXa/mΔΦ/radXa/mΔΦ/rad30 000.50.699 130 001.00.699 130 001.50.699 130 002.00.699 130 002.50.699 130 003.00.699 130 003.50.699 030 004.00.699 030 004.50.699 030 005.00.699 051 841.756.166 051 842.256.166 951 842.756.168 151 843.256.169 651 843.756.171 751 844.256.174 851 844.756.179 851 845.256.189 051 845.756.212 851 846.256.403 970 000.56.745 070 001.06.745 070 001.56.745 070 002.06.745 070 002.56.745 070 003.06.745 070 003.56.745 170 004.06.745 170 004.56.745 170 005.06.745 1
3.2 等角度不等距的不同目标的相位分布
取FDA初始频率f0为1 GHz、阵元间距d为0.15 m、阵元数N为5、时间t为0,目标距离FDA阵元初始点的y轴距离Ya为Xasinθ,频率增量Δf分别为0、1 kHz,取目标距离FDA阵元初始点的x轴距离Xa为变量,分别求取传统相控阵和FDA的相位分布.
① 当θ为π/4时,仿真结果如图6所示.
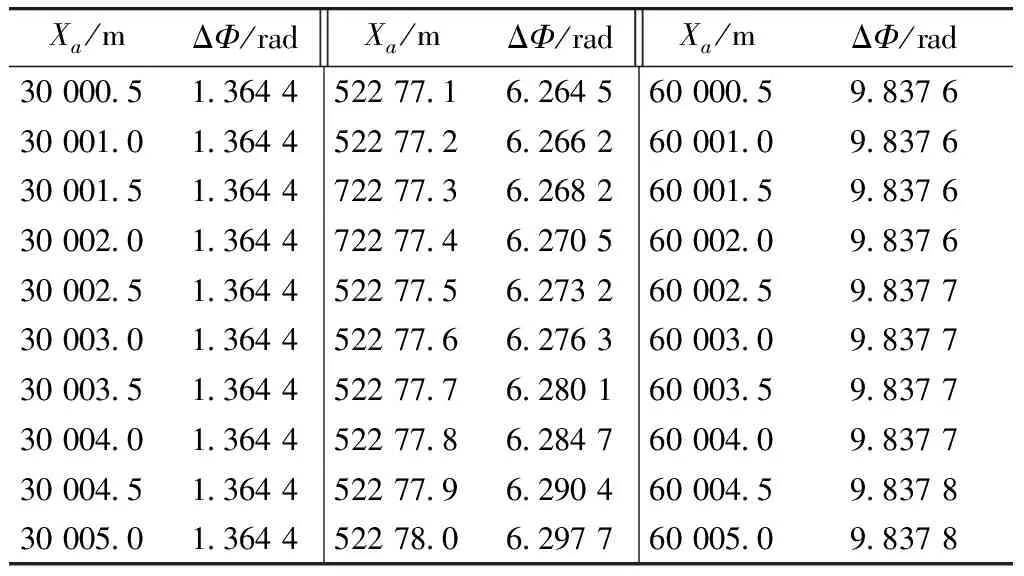
当θ为π/4时,由不同Xa下相控阵和FDA相位变化图形可以看出,FDA相位变化与相控阵相位变化趋势基本一致;但是,相同Xa下FDA相位会比相控阵相位超前,因而得到不同Xa下相位差ΔΦ的变化数据如表3所示,由表中数据可以看出,当Xa变化时达到52 277.75 m左右,即距离R0为739 31.90 m时,FDA相位会超前相控阵相位2π,即一个周期.
表3θ为π/4时,不同距离上相控阵与FDA的相位差
Tab.3 Phase difference of phased array and FDA at different distances,whenθ=π/4
Xa/mΔΦ/radXa/mΔΦ/radXa/mΔΦ/rad30 000.51.364 430 001.01.364 430 001.51.364 430 002.01.364 430 002.51.364 430 003.01.364 430 003.51.364 430 004.01.364 430 004.51.364 430 005.01.364 4522 77.16.264 5522 77.26.266 2722 77.36.268 2722 77.46.270 5522 77.56.273 2522 77.66.276 3522 77.76.280 1522 77.86.284 7522 77.96.290 4522 78.06.297 760 000.59.837 660 001.09.837 660 001.59.837 660 002.09.837 660 002.59.837 760 003.09.837 760 003.59.837 760 004.09.837 760 004.59.837 860 005.09.837 8
② 当θ为π/6时,仿真结果如图7所示.
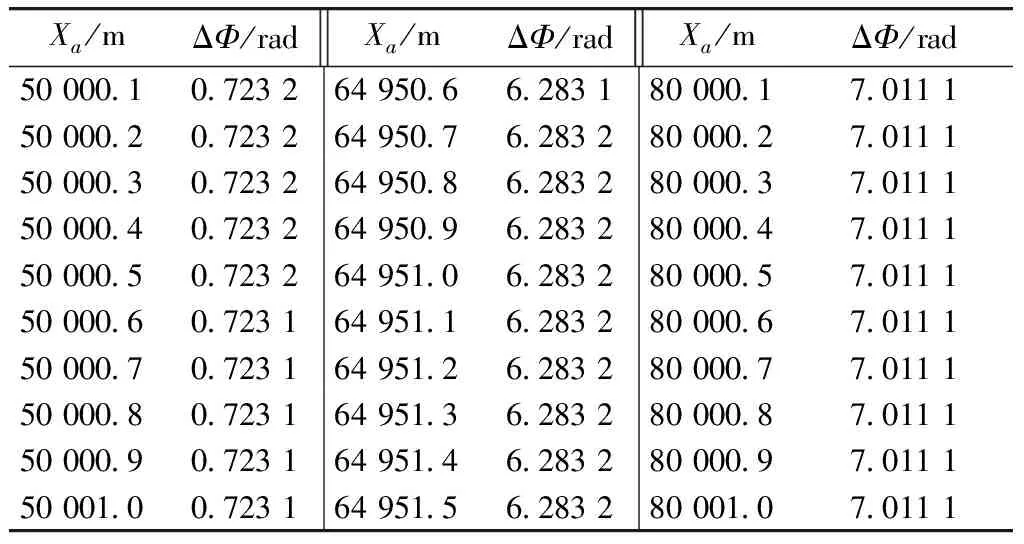
当θ为π/6时,由不同Xa下相控阵和FDA相位变化图形可以看出,FDA相位变化与相控阵相位变化趋势基本一致;但是,相同Xa下FDA相位会比相控阵相位超前,因而得到不同Xa下相位差ΔΦ的变化数据如表4所示,由表中数据可以看出,当Xa变化时达到649 50.7 m左右,即距离R0为74 998.90 m时,FDA相位会超前相控阵相位一个周期.
Tab.4 Phase difference of phased array and FDA at different distances,whenθ=π/6
Xa/mΔΦ/radXa/mΔΦ/radXa/mΔΦ/rad50 000.10.723 250 000.20.723 250 000.30.723 250 000.40.723 250 000.50.723 250 000.60.723 150 000.70.723 150 000.80.723 150 000.90.723 150 001.00.723 164 950.66.283 164 950.76.283 264 950.86.283 264 950.96.283 264 951.06.283 264 951.16.283 264 951.26.283 264 951.36.283 264 951.46.283 264 951.56.283 280 000.17.011 180 000.27.011 180 000.37.011 180 000.47.011 180 000.57.011 180 000.67.011 180 000.77.011 180 000.87.011 180 000.97.011 180 001.07.011 1
③ 当θ为π/3时,仿真结果如图8所示.
当θ为π/3时,由不同Xa下相控阵和FDA相位变化图形可以看出,FDA相位变化与相控阵相位变化趋势基本一致;但是,相同Xa下FDA相位会比相控阵相位超前,因而得到不同Xa下相位差ΔΦ的变化数据如表5所示,由表中数据可以看出,当Xa变化时达到37 499.45 m左右,即距离R0为74 998.61 m时,FDA相位会超前相控阵相位一个周期.
表5θ为π/3时,不同距离上相控阵与FDA的相位差
Tab.5 Phase difference of phased array and FDA at different distances,whenθ=π/3
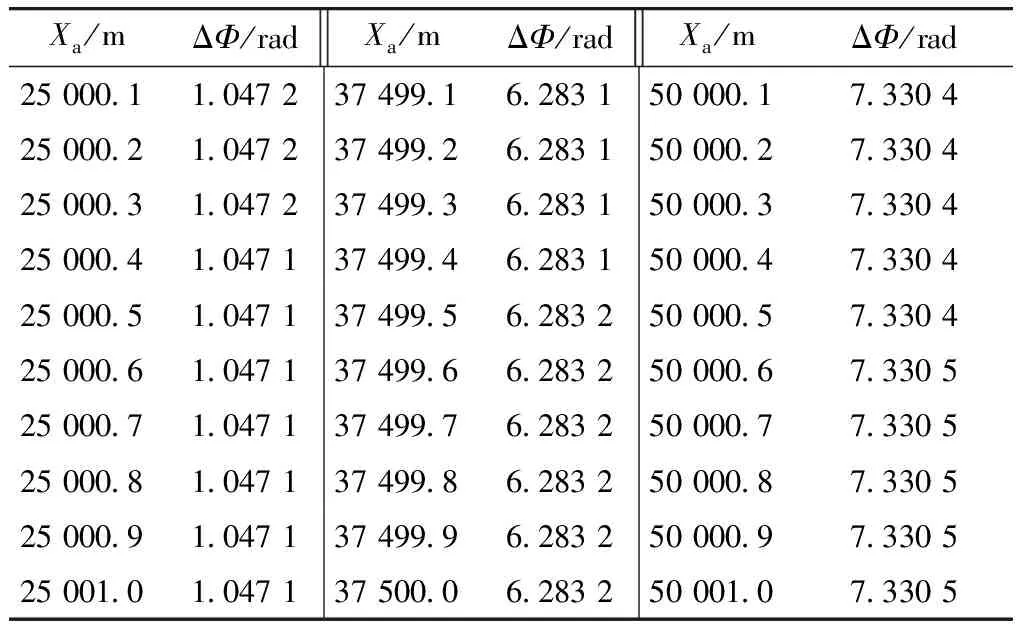
Xa/mΔΦ/radXa/mΔΦ/radXa/mΔΦ/rad25 000.11.047 225 000.21.047 225 000.31.047 225 000.41.047 125 000.51.047 125 000.61.047 125 000.71.047 125 000.81.047 125 000.91.047 125 001.01.047 137 499.16.283 137 499.2 6.283 137 499.36.283 137 499.46.283 137 499.56.283 237 499.66.283 237 499.76.283 237 499.86.283 237 499.96.283 237 500.06.283 250 000.17.330 450 000.27.330 450 000.37.330 450 000.47.330 450 000.57.330 450 000.67.330 550 000.77.330 550 000.87.330 550 000.97.330 550 001.07.330 5
综合比较θ为π/4、π/6、π/3时FDA和相控阵分布图,可以看出达到FDA和相控阵相位分布趋势基本一致;但是,相同Xa下FDA相位会比相控阵相位超前,而FDA相位会超前相控阵相位一个周期时,且此时距离R0均为75 km附近.
3.3 以阵元中点为圆心的圆面上不同目标的相位分布
取FDA初始频率f0为1 GHz、阵元间距d为0.15 m、阵元数N为5、时间t为0,目标距离FDA阵元初始点的y轴距离Ya为5 km,频率增量Δf分别为0、1 kHz,取目标距离FDA阵元初始点的x轴距离Xa为变量,分别求取传统相控阵和FDA的相位分布. 仿真结果如图9.以阵元中心为圆心的圆面上不同目标的相位分布如表6所示.

表6 以阵元中心为圆心的圆面上不同目标的相位分布
由图9和图10可以看出,在以阵元中心为圆心的圆面上不同目标的相位分布,无论是传统相控阵还是FDA,其相位均几乎保持不变,即该圆面可以近似认为为相控阵和FDA的同相波前,即等相位
面,因此,可以看出FDA与相控阵的同相波前分布相似,均可以近似为以阵元中心为圆心的圆面.
4 结 论
针对频率分集阵列雷达的相位方向图问题,研究了FDA波束相位方向图特性.
① 提出了研究FDA空间相位分布的两种模型,分别为模型建立法和欧拉公式法. 通过仿真,比较论证了两种方法求解相位的特点.
② 根据提出的欧拉公式法所建立的相位分布模型,仿真作出了FDA波束相位方向图,并与传统相控阵相位方向图对比,比较了FDA波束相位方向图与传统相控阵的差异性和相似性.
③ 根据提出的欧拉公式法所建立的相位分布模型,研究了FDA波束在等高线、等角度线和以阵元中心为圆心的圆面上不同目标的相位分布,并与传统相控阵作对比,分析了FDA和传统相控阵相位分布特性.
④ 得到了FDA波束的同相波前,即等相位面的分布,即可以近似认为为以FDA阵元中心为圆心的圆面.
综上研究,FDA波束相位分布规律与传统相控阵相位分布规律相似,而由于微小频差带来的相位变化仅影响相位的大小变化,并不影响相位的分布趋势.

