曲面上不倒翁的力学稳定性分析

（杭州外国语学校，浙江杭州 310000）

1.背景介绍

1.1 研究背景与意义

不倒翁是生活中常见的传统玩具，最早关于不倒翁的历史文献记载出现于唐代。当时的不倒翁具有人的形态，通过把器物底端做的比其顶端更重，从而使该器物在受力以后仅在一定范围内摇动，而不会摔倒，故而取名为“不倒翁”。据考究，在距今6000～7000年前的半坡遗址，人们就已经发现了类似于不倒翁的提水工具。当该提水工具装水时，由于自重改变会发生一定的倾斜，然而当其装满水后，人们发现该提水工具又会慢慢直立起来，与现代的不倒翁别无二致。

由于不倒翁违背了生活中物体在受到水平推力后容易倾倒的直观经验，因而这类“反常”的玩具深受人们喜欢，在不倒翁“推不倒”的背后隐藏着非常丰富的力学原理。得益于现代完备的物理力学分析体系，我们能对不倒翁的力学原理做出完满的解释。如今，不倒翁的力学原理已不局限于玩具，在建筑领域，应用不倒翁的原理可使建筑物更加稳定。在生活用品方面，不倒翁原理的应用也使易碎的物品不易摔倒，更加持久耐用。

本文借助力矩这一物理学工具，对不倒翁背后的力学原理进行了简要分析。同时，本文将不倒翁应用于曲面环境，探究了其稳定极限。通过本文分析，将不倒翁在平面上平衡条件结论推广到了曲面，从而为研究曲面上物体的平衡提供了相应的理论指导。

1.2 国内外研究现状

对力学系统的稳定性分析相关介绍已有多篇文献述及，黄开志对不倒翁在圆形曲面上的动力学方程进行了分析[1]，对不倒翁在无滑动滚动条件下的“恢复”条件进行了研究，在此基础上得出了对应的动力学参数方程，并在计算机上进行了数值验证，结果显示不倒翁在曲面上的摆动周期与其初始摆角近似成线性关系。张晓华对高维非线性力学系统的稳定性、分叉以及混沌问题进行了研究[2]，

通过数值模拟与解析求解两条途径分析了非线性系统的稳定性，结果很好地解释了非线性动力学系统的行为。许胜才对加固边坡的力学稳定性进行了详细探究[3]，通过理论分析、数值仿真以及实验的方法对边坡的抗滑等力学性能进行了检验，具备一定的工程实用价值。姚展环对结构力学中的复杂问题进行了近似求解[4]，通过引用分配系数这一概念，极大简化了所研究力学系统的方程个数，从而使问题在一定精度范围内得到近似求解。宋建钦利用力矩平衡这一工具[5]，提出了日常生活中对车辆重心以及偏重进行理论测量的方法，从而使上述测量简单易行，具备一定的实用价值。

2.力矩平衡与不倒翁的基本原理

2.1 力矩与力矩平衡

本文在研究不倒翁的稳定性过程中，将不倒翁视为一个理想的刚体。所谓刚体即在运动和力的作用下，其形状不发生改变，并且其内部各点相对位置不发生变化的物体。在现实生活中，绝对刚体是不存在的。考虑到一般不倒翁在受力时其形变程度与其自身的几何尺寸相比十分微小，可忽略不计，因而本文在研究不倒翁的稳定性时将不倒翁视为理想刚体处理。

刚体转动时的运动状态由施加在刚体上的和外力矩决定。力矩是描述力对物体转动作用的物理量，其基本公式可从杠杆原理引出。由杠杆原理可知，对于分别位于杠杆两端的重物，其自身重力与杠杆转轴到重力作用线距离(力臂)的乘积相等。可见，力与其对应力臂的乘积描述了该力对杠杆这一刚体的转动效果，称之为力矩，表达式如下：

式(1)中：F表示刚体所受的力，d为该力对转轴的力臂，即转轴到力F作用线垂线段的长度，M表示力F对应的力矩。

力矩平衡即合外力矩为零的情况。以杠杆平衡为例，杠杆两端的重物自身重力与杠杆转轴到重力作用线距离的乘积相等，即两力矩的大小相等。但两力矩的作用效果不同，刚好相反，因此两力矩相互抵消，合外力矩为零，我们说杠杆处于力矩平衡状态。本文所研究的不倒翁稳定性的临界状态即为不倒翁所受的和外力矩为零，即力矩平衡的情况。

2.2 不倒翁的基本原理

上文对刚体以及力矩的基本概念进行了介绍，由于不倒翁受力不会产生明显的形变，因此可将不倒翁当作刚体处理。如图1所示，给出了一个不倒翁的简化示意图。图中左边的不倒翁处于平衡状态，其重心位于点o，此时不倒翁仅受到重力mg和水平面给他的压力FN，二力大小相等，方向相反，并且位于同一作用线上。因此左边不倒翁所受的合外力为零，合外力矩也为零，处于平衡状态。

图1 不倒翁基本原理示意图

当不倒翁受到一定的扰动，如图中右边不倒翁所示，不倒翁所受重力mg与压力FN不再位于同一作用线上，其所受合外力不再为0。若以不倒翁与水平面的接触点o'为转轴，由于水平面对不倒翁的支持力的作用线通过转轴o'，力臂为0，因而其所产生的力矩也为0。此时不倒翁所受合外力矩仅由不倒翁自身重力产生，大小等于不倒翁自身重力与接触点o'到重力作用线距离的乘积，在该“扶正”力矩的作用下，不倒翁有向平衡位置转动的趋势。

在理想条件下，不倒翁可以以固定周期不断左右摆动下去，但在实际生活中，因为空气阻力以及不倒翁与水平面摩擦等因素的影响，不倒翁最终会停在如左边不倒翁所示的平衡位置，由此达到不倒的效果。

图1所示的不倒翁重心位于简易模型圆心的下方，从而在不倒翁偏离平衡位置时产生一个“扶正”力矩，使不倒翁具有回到原平衡位置的趋势。若不倒翁重心位于简易模型圆心的上方，不倒翁偏离平衡位置时重力产生的力矩效果将使不倒翁更加偏离其原平衡位置，从而加速不倒翁的倾倒过程。故不倒翁要想实现“不倒”效果的必要条件是其自身重力在不倒翁偏离平衡位置时产生相应的“扶正”力矩，对应于不倒翁的具体结构来说，要求不倒翁的重心要低。

3.曲面上不倒翁的稳定条件

上文对不倒翁在平面上的稳定性进行了详尽分析，解释了不倒翁能够自动回复到平衡位置的机理。日常生活中，不倒翁的放置环境可能并不平坦，当将不倒翁放置在具有一定曲率的曲面上时，由生活经验可知，不倒翁将存在一个最大稳定偏角。当不倒翁的轴线偏离竖直方向的角度超过该最大稳定偏角时，不倒翁将产生倾覆。如图2所示。

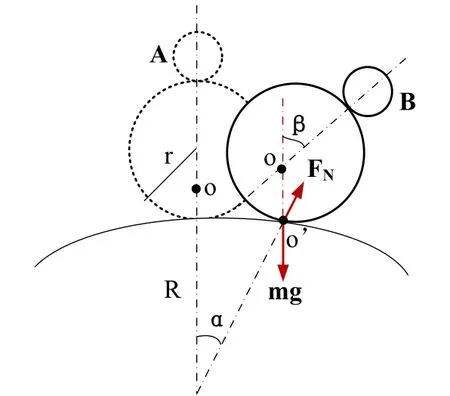
图2 曲面上不倒翁临界示意图

假设不倒翁的下部为一半径等于r的圆的不倒翁，位于半径等于R的曲面上，不倒翁重心点o位于半径的1/2处。初始时不倒翁处于A状态，合外力等于零，所受合外力矩也等于零，不倒翁处于平衡状态。当不倒翁受到扰动而偏离平衡位置后，由于不倒翁所受曲面的支持力始终通过不倒翁与曲面的接触点，因而以接触点o'为转轴，不倒翁所受曲面支持力的力臂始终为零，其产生的力矩也恒为0，不倒翁将在重力作用下绕接触点o'转动。

当不倒翁轴线偏离竖直方向的夹角不大时，不倒翁自身重力所产生的力矩仍为“扶正”性质，因而不倒翁将在该力矩的作用下回复到原平衡位置。然而，当不倒翁轴线偏离竖直方向的夹角较大时，不倒翁自身重力产生的力矩将加速不倒翁的倾倒，从而使不倒翁在该曲面上失去稳定。上图给出了不倒翁在临界状态时的位置(状态B)，即所受重力的作用线过其与曲面接触点o'且不倒翁不处于初始状态，此时重力mg与压力FN的力臂都等于零，即合外力矩等于零，不倒翁处于临界状态，此时定义重力作用线与轴线的夹角即为不倒翁在该曲面上的最大稳定偏角β。由于不倒翁与曲面不打滑，因而不倒翁滚过的弧长与曲面上通过的弧长相等，即图中角α与偏角β之间满足下述关系：

图中曲面对不倒翁的支持力过不倒翁的圆心，对以不倒翁圆心、重心以及不倒翁与曲面的接触点构成的三角形应用正弦定理可得：

将式(1)代入式(2)中，可得下式：

取特例，当R/r=2时，可得如下超越方程，观察可知该超越方程存在一个解为β=90°，即不倒翁的轴线可最大偏移至水平位置而不发生倾倒。

由式(3)可知，当曲面越平坦时，即R越大时，不倒翁与竖直面的最大偏角也就越大，从而不倒翁的稳定性就越好。当不倒翁的重心o'点越低时，可获得更大的临界偏角，在该偏角以内，不倒翁均能恢复原先的平衡状态(A状态)，不倒翁的稳定性越好。同理，当不倒翁底面等效圆的半径r越小时，不倒翁越不容易倾倒，稳定性越好。

4.结论

本文对不倒翁这一传统玩具进行了力学分析，借助力矩这一物理工具，对不倒翁在平面上“不倒”的原理进行了理论解释，指出重力产生的“扶正”力矩是不倒翁能够做到恢复原平衡状态的关键，且为使重力对不倒翁的力矩为“扶正”性质，不倒翁的重心应当足够低。在此基础上，本文对曲面上不倒翁的稳定性条件进行了探究，找到了不倒翁在曲面上保持稳定的临界条件，并在该临界条件下求取了不倒翁的最大稳定偏角。研究结果表明，不倒翁在曲面上存在某一最大稳定角度，当不倒翁轴线偏移超过该角度时，不倒翁的稳定性将遭到破坏。进一步分析可知，不倒翁在曲面上的临界稳定角度与其重心位置、放置不倒翁的曲面曲率半径以及不倒翁地面等效圆的半径均有关。本文对平面上不倒翁的平衡条件进行了合理外推，从而为分析曲面上物体的平衡提供了相应理论指导。