带时间窗的煤炭企业轴辐式网络转运中心选址
何茵楠,吴传良 (淮南师范学院 经济与管理学院,安徽 淮南 232000)
煤炭是我国的基础能源也是不可再生能源,在我国能源消费结构中占据主导地位,是促进我国经济和社会发展不可或缺的资源。虽说近年来,我国大力鼓励开发和使用清洁能源,但由于我国尚处于高速发展时期,城市设施建设还在完善,主要耗煤的生产和制造商如石化、冶金、建材、电力等也持续保持高速发展,再加上清洁能源的开发和使用的成本较高,使得短时间内煤炭不会被清洁能源完全替代为主要的消耗品。而我国的煤炭资源分布与煤炭消费地分布的差异性,凸显了煤炭物流的重要性,大量的煤炭多次且长距离的转运成为煤炭运输的主要特点,转运中心在整个煤炭物流网络中扮演着至关重要的角色,它相当于一个枢纽点,把各运输通道连接起来,以保证各地区煤炭的供需平衡。
由于终端用户的煤炭价格有很大部分都是由物流运输的费用承担,所以优化煤炭物流运输网络,通过建立转运中心,进而缩减煤炭企业的运输费用,提高企业利润,是十分必要的。而转运中心的选址要从各方面综合考虑,这里的转运中心其实相当于轴辐式物流网络中的一个枢纽点,利用轴辐式物流网络的规模效应,可以大大减少运输成本。除此之外,各方面还不够系统化的煤炭配送网络,导致煤炭物流无法合理高效的组织和运营,这些都足以导致对需求用户的用煤成本和煤矿企业的利润以及社会的能耗水平造成不良的影响。同时大多数煤炭企业在给客户配送煤炭时,都不会考虑时间的问题。当出现用电的高峰期,电力企业煤炭的需求是很急切的,而且当今社会是买方的社会,在供大于求的市场条件下,在客户满意的时间范围内送达,才能够长久的留住客户。最重要的是煤炭的价格每天都在波动,所以说煤炭物流配送对时间的敏感度是很高的,要站在顾客的角度对时间进行约束,引入时间满意度函数,使选址结果更合理。
轴辐式网络枢纽设施选址是由O'Kelly[1]首次提出的,接着又建立了一个二次整数规划模型用来解决单分配枢纽中位的问题,并运用启发式算法求解,该算法将每个非枢纽节点与其距离最近的一个枢纽节点相联系或分配给最近的两个枢纽节点中的任意一个。O'Kelly[2]指出枢纽在整个输运网络中尤其重要,但是建设和操作的成本非常大,不能被忽略,因此在讨论系统运输费用时加入了枢纽特定固定成本费用,并在建立模型的时候首次加入了枢纽个数这一决策变量对整体进行了改进,以运输成本总最小为目标,采用二次离散整数规划的方法进行网络设计。Campbell[3-4]首次提出多分配P中值问题,并且指出该问题是属于NP-hard问题。紧接着Campbell又引入P中心和中心点覆盖问题,并考虑了路线修建的成本和容量限制问题。Abdinnour-Helm&Venkataramanan[5]提出了一种新的二次整数方程,用于解决无容量限制,这种新的方程利用分支定界法去找到最佳的方案。Mayer[6]等人在分支定界算法基础上,运用聚合模型公式和平面枢纽选址的经验为此设计了一个简单的启发式算法,该算法能够在合理的时间内求解出40个节点规模中的最优解。Ramez Kian&kamyar Kargar[7]比较了割平面法和分制定界法对解决轴辐射网络状态下中心选址问题的优缺点。然而非线性问题非常难以解决,把非线性转变成线性问题是解决问题的关键。Wajeb Gharibi[8]运用一种新的割平面算法去解决二次0-1规划问题。大多数中心选址问题都是用简化的成本结构和复杂的货运量去考虑问题,由于货运量只能用概率近似分布,所以Peiman Dabidian&Uwe Clause[9]等人考虑了车辆和枢纽能力的规划这一个因素,从而去解决中心选址问题。
在时间满意度为目标的选址方面,Jiuh-Biing Sheu[10]在设施具体位置、枢纽数量和服务范围确定的基础上,采用运筹学中的整数规划和层次聚类分析法进行分析,然后构建以网络总成本最小、客户满意度最大化和企业利润最大的多目标规划模型。Wang Zhuan[11]等人分析4/R/I/T结构的配送网络,提出0-1整数规划模型,模型主要以运输成本最小为目标,同时又把服务的时间和服务的关系对模型的总目标进行约束,最后用lingo软件求解。Osvald&Stirn[12]提出了时间窗口的概念,构建了易腐物品的损失率与货物载重量以及运输时间的函数关系式,以对易腐物品运输车辆路径的优化来减少运输时间,从而减少易腐蚀物品的损失率。Shankar[13]等人认为供应链结构中的四个阶段:制造商、供应商、配送中心和客户,形成了产品流动所经过的四段过程,所以通过对四个阶段的分析构建了以网络总成本最小和客户满意度最大为目标的选址模型。
目前,国内外学者在对煤炭物流网络优化研究方面,主要是从配送中心选址[14-16]、配送路径优化[17]以及煤炭采购物流优化[18-20]等方面来考虑。综合国内外研究可以看出,多数研究还是集中于总体成本最小为主要目标,同时再考虑客户时间满意度最大的比较少见,在煤炭需求的高峰期,在规定的时间把煤炭运输到客户手中,在当今供大于求的煤炭市场中尤为重要。基于以上研究背景,借鉴国内外相关研究,本文将物流运输费用最小和时间满意度最大两者加以均衡,通过建立模型,对转运中心选址问题进行研究。
1 问题描述与模型构建
1.1 问题描述及假设
供应地是煤炭企业的洗选中心且数量为一个,备选点也就是备选转运中心,是企业有长期合作的煤炭用户所在地的周边铁路站点,需求点对应的是与企业有长期合作的多个客户。
为了便于分析问题,现对该模型做出如下假设:
(1)网络中供应地数量为1,备选点的集合为n,需求点的集合为S,枢纽节点的数量为p;
(2)两个节点之间必须至少经过1个枢纽节点且最多经过两个枢纽节点;
(3)非枢纽节点之间不能直接相连;
(4)运输方式采用铁路和汽运联运的运输,枢纽点与枢纽点之间存在运输折扣系数;
(5)各节点容量都可以满足需求地的需求量;
(6)运输和配送时间只与距离和速度有关,不考虑其他情况;
(7)顾客所期望的服务时间范围和最大容忍时间已知;
(8)货物的运输都是整批的单向的运输,都是一次性可以完成运输,不用多次运输。
1.2 参数和变量
a:枢纽点之间因规模效应产生的运输成本折扣因子;Cik:从节点i到枢纽点k之间单位流量单位距离的运费率;Cjm:从节点j到枢纽点m之间单位流量单位距离的运费率;Ckm:从枢纽点k到枢纽点m之间单位流量单位距离的运费率;Ck:枢纽节点的建设成本;F (tij):需求点j的客户对供应地i的时间满意度函数;Lik:节点i到枢纽点k的距离;Lkm:枢纽点k到枢纽点m的距离;Ljm:枢纽点m到节点j的距离;n:备选枢纽点的总数;s:需求点j的总数;p:枢纽点的数量;To:需求点的顾客感觉满意时所接受的最长等待时间上限;Tj:需求点的顾客感觉不满意时所接受的最短等待时间下限;V1:火车满载速度;V2:汽车满载速度;Wij:从节点i到需求点j的运量;Xk:若节点k被选为枢纽节点,则Xk=1,反之Xk=0;Xijkm:节点i到j之间的流通货物是否通过枢纽点k,m的0-1变量。
1.3 时间满意度函数
时间满意度可以定义为当企业开始响应顾客的订单一直到运送客户手中所消耗的时间对顾客而言的满意程度。时间满意度函数的表达形式有很多,根据不同的实际问题在实际调查的基础上可以拟合到不同的函数,函数图像因不同的客户呈现出可连续的或者离散的,其中时间满意度函数的连续函数中又可以分为线性的和非线性的。本文采用的是线性时间满意度函数,设网络中节点个数为n个,tij为供应地i将货物运送到需求点j的服务时间,To是需求点j的客户感到相当满意可以接受的最长等待时间的上限,Tj是需求点j的客户感到不满意时所能接受的最短等待时间的下限。F (tij)是需求点j的客户对供应地i的时间满意度函数且。从图1中可以看出,若顾客在[0,To]时间内被服务,时间满意度最大且为1,如果在[To,Tj]时间内获得服务,时间满意度则会随着等待时间的增加而减少,如果在[Tj,∞ ]时间内被服务,则时间满意度为0。详情见图1和式1。

1.4 模型的构建
综合考虑网络节点之间的流量、单位运输的成本、枢纽之间的规模经济效益和枢纽点建设的固定成本等因素,以总物流运输总费用最小为目标,同时再以顾客时间满意度水平最大为目标,构建轴辐式物流网络枢纽选址模型,笔者采用铁路运输与公路运输共同联运的方式。

图1 线性时间满意度函数
目标函数:

约束条件:
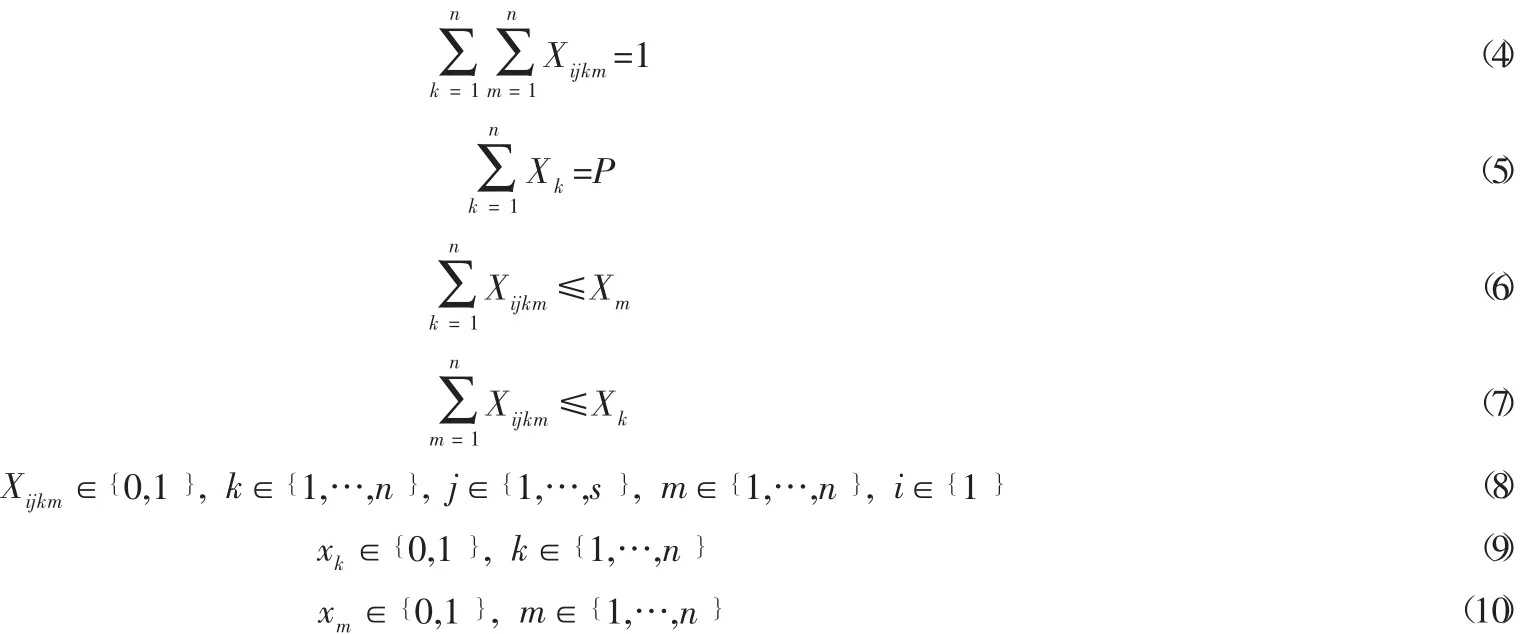
上述模型中有两个目标函数,第一个目标函数式(2)以系统总费用最小为目标,主要分为两个部分,等号右边的第一部分是非枢纽点与枢纽点之间、枢纽点与枢纽点之间、枢纽点与非枢纽点之间的总运输成本之和,等号右边第二部分是建设枢纽节点的固定成本。第二个目标函数式(3)是以客户时间满意度最大为目标,这里的时间满意度函数F (tij)是前文提到的线性的时间满意度函数,时间用路程除以速度表示。约束式(4)表示从供应地i到需求点j必须经过枢纽节点进行中转,不允许直接运输;约束式(5)表示整个轴辐式网络中枢纽点的数量是P个;约束式(6)和式(7)表示只有当k,m为枢纽节点时,从节点i到节点j才能经过k,m;约束式(8)为0-1变量,当节点i到j之间的流通货物经过k,m时,Xijkm=1,反之Xijkm=0;约束式(9)、式(10) 为0-1变量,表示若节点k被选为枢纽节点,则Xk=1,反之Xk=0。
2 模型求解
本模型除了考虑系统费用最小的情况外,还考虑了顾客时间满意度最大的情况,因此属于多目标选址模型问题,为了避免多目标求解时出现背反现象,在解决多目标求解问题时,为了使求解更简单,常常会把多目标转换成单目标然后进行求解,一般常见的有两种方法:加权法和约束法。加权法是分别给多个目标函数赋予既定的权重值,通过加权方法,把多目标转化成单目标,方便求解。约束法就是将次要的一个或者多个目标转变为约束条件,最终只留一个最终的目标函数。根据本文选址的侧重点,把系统费用最小为主要的目标进行求解,把顾客时间满意度变为约束条件,用β表示需求地客户的最低时间满意度水平要求。因此模型转换成单目标函数:

增加约束条件:

最终的模型:

约束条件:

求解模型的软件有很多,方法也有很多,在转换为单目标后,根据模型的特点和性质,为了求解更简单方便,本文选择用AMPL软件调用MINOS5.51求解器进行求解。
3 算例应用
3.1 算例分析
本文以HB矿业集团为例,对HB矿业集团的多个长期客户所在地进行了比较和分析,最终决定根据客户的所在地选择合适的转运中心,因此本文供给地是1个用I0表示,备选枢纽点也就是备选转运中心的数量为5个,分别用J1、J2、J3、J4、J5表示,备选枢纽点都是长期合作客户所在地周边的火车站点。根据内部调查企业长期合作的客户有7个,所以需求地的数量为7 个,分别用 I1、I2、I3、I4、I5、I6、I7表示。
(1)供应地到备选地之间的距离如表1所示:

表1 供应地到5个备选枢纽点之间的距离 单位:公里
(2)备选枢纽点之间的距离如表2所示:

表2 备选枢纽点之间的距离 单位:公里
(3)备选枢纽点到需求点之间的距离如表3所示(数据来源百度地图):

表3 备选枢纽点到需求点之间的距离 单位:公里
(4)需求点的年需求量如表4所示 (数据来源于企业内部资料):
(5)需求点的容忍时间范围如表5所示(数据来源企业内部资料):

表5 需求点容忍时间范围 单位:小时
(6)备选枢纽点的固定建设成本如表6所示(数据来源于企业内部资料):

表6 固定建设成本 单位:万元
(7)其他参数设定。本文采用联运的方式,供应地到备选枢纽点和备选枢纽点之间都采用铁路运输,由于备选枢纽点到需求地之间比较近,所以采用汽车运输方式。其他参数如表7所示:
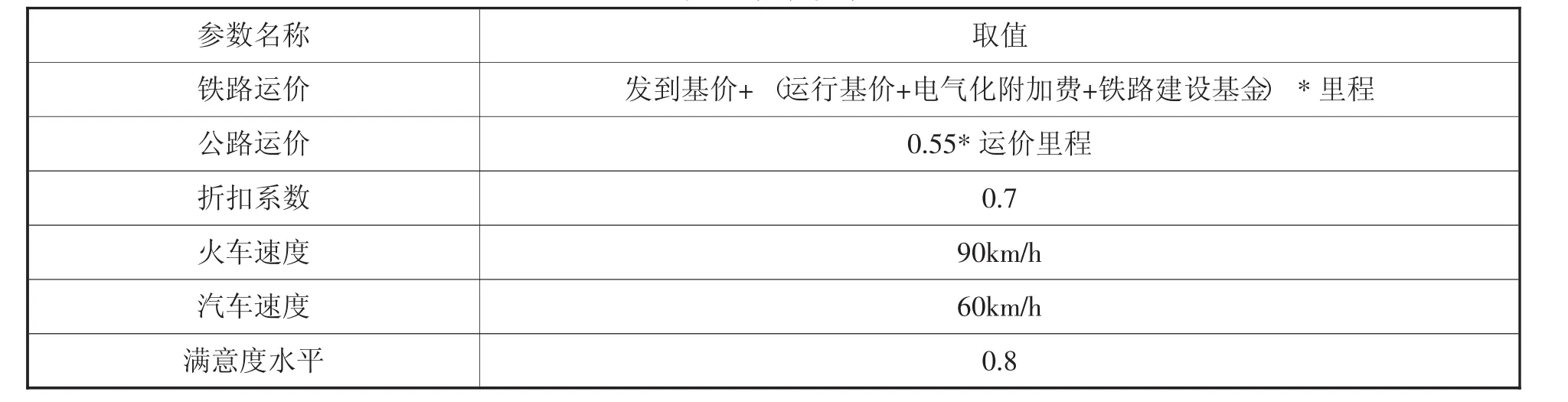
表7 其他参数
3.2 实验结果与分析
使用求解器MINOS5.51并结合所用数据,根据所建模型利用AMPL编写模型的程序。经过优化计算,转运中心Xk的结果如图2所示,由以上计算结果可以得到该算例中转运中心的选择为:J1、J4。
转运中心和非转运中心的链接情况如图3所示。
根据优化计算出的结果如图3。所计算出来的枢纽点的数量如果太多会增加运输时间,同时总成本费用也会增加,而枢纽节点的数量如果太少,那么就达不到规模效益。经过计算可得出本案例应选择两个转运中心且目标函数值最优,约为757 494 769元,相较于企业之前的物流运输模式,大大减少了总成本,间接增加了企业的效益。

图2 所选枢纽节点结果

图3 各点连接情况
4 结论
转运中心可以在煤炭需求高峰的时期,在节约运输总费用的前提下,快速的送达客户手中。研究发现,利用轴辐式物流网络结构,考虑时间满意度,建立适当数量的转运中心使得企业煤炭运输系统降低了总成本费用,稳定性更高,同时站在客户的角度去考虑时间约束问题,更加人性化。转运中心的建立还可以降低灾难性气候或者拥堵对煤炭的正常运输,在煤炭告急的时候也可以担任存储的角色,而且轴辐式网络的规模效益要大于点对点传统的运输模式,节约物流资源,减少运输拥堵。
本文在选址模型的算例中,将单位运输成本设为固定值,在实际运输中,由于地理位置、天气、道路状况等因素的影响,单位运输成本是变化的,在未来的研究中可以给予这方面的考虑。

