基于改进离散粒子群算法的生鲜农产品配送路径设计

孙宗军，马佳玉，徐海鑫 SUN Zongjun,MA Jiayu,XU Haixin

（山东科技大学 交通学院，山东 青岛 266590）

(Transportation College,Shandong University of Science and Technology,Qingdao 266590,China)

0 引言

运输成本的控制一直是物流行业的热点问题之一，因生鲜农产品的配送对时效性、准确性要求较高，生鲜农产品的高运输成本成为制约生鲜农产品物流体系发展的难点，优化配送路径是提高配送效率、降低运输成本的重要方法[1]。目前，生鲜农产品的配送路径优化常采用传统的路径优化方式[2]，即运输车依次经过需要配送的n个站点再回到始发点，求解最短路径。然而，传统的路径优化往往无法得到真实的最短路径，增加了运输成本。本文通过改进的粒子群算法[3]，以RH农场为例，对其生鲜农产的配送进行了路径优化，降低配送成本。

1 RH农场的基本概况及现状分析

RH农场的主要生鲜农产品包括水果类、蔬菜类、肉类、花类等。对市区范围内的18个配送点进行了地理数据采集，RH为农场，A、B为现有的两家门店，C为虚拟配送中心，如图1和图2所示。

2 改进粒子群算法

粒子群算法采用实数编码是其显著优点，不需要采用二进制编码来进行最优解的运算。在设置好适应度函数后就可进行搜索最优解，直到满足中止条件后终止运算。

2.1 TSP离散型粒子群算法

程毕芸[4]提出了搜索混沌离散粒子群优化算法，优化后的粒子群算法参数如式（1）和式（2）所示。

粒子的更新后速度：

粒子的更新后位置：

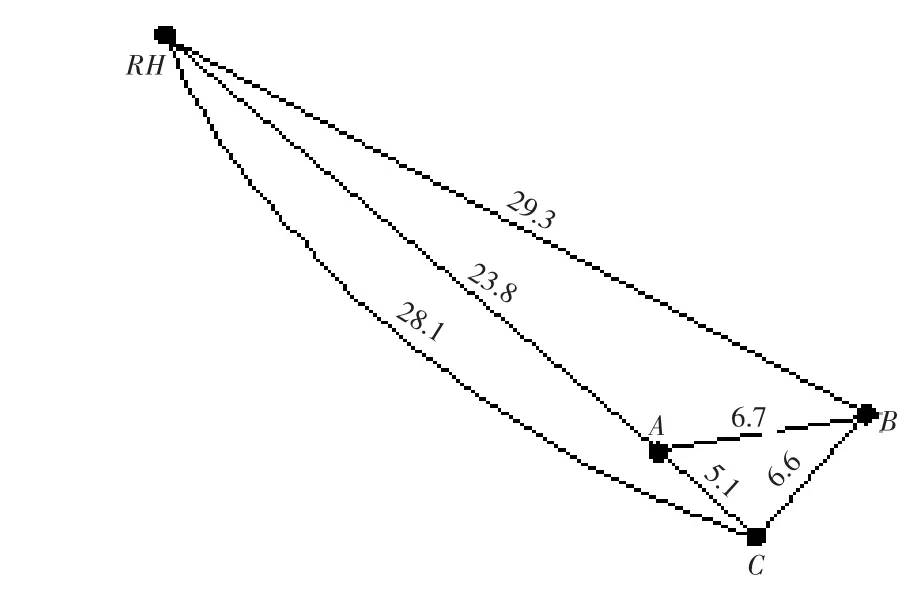
图1 RH与各配送中心相对位置示意图

图2 RH与各配送点相对位置示意图

当配送点的个数小于等于30时，迭代次数达到60左右即可达到最优。本文中配送点个数有18个，设置迭代次数设为60，粒子数为200。

2.2 2SGPSO算法改进

2SGPSO算法在解决物流运输路径问题时，首先利用GPSO算法对配送站点序列进行搜索寻优操作，得到最优配送站点序列和最短距离。然后利用2SA算法对GPSO算法得到的最优配送站点序列进行操作，最终得到的最优配送站点序列和最短路径距离。操作流程如下所示[4]。

输入：粒子群个数、配送点个数、配送点坐标

（1）初始化粒子速度及位置。

（3）根据公式更新粒子位置速度。

输出：Gbest

2.3 ACPSO算法改进

ACPSO中设n个需要经过的点，任选其中第j1次和第j2次经过的点，在路径C0中将第j1次和第j2次经过的点进行交换，其余点顺序不变，变化后的路径定义为C1；n个点，任意选取一个交叉区域，将old2的交叉区域添加至old1中随机选取的位置，且将old1在old2交叉区中已经过的点删除。操作流程如下[5]：

输入：粒子群、配送点个数、配送点坐标、最大迭代次数、随机产生对个数的初始解C0

（1）初始化粒子速度及位置。

（3）根据公式进行更新位置：

若：第j个粒子的路径C0（j）与个体最优交叉得到C1（j），C1（j）同Gbest交叉到C2（j），C2（j）经过变异操作变为下一次迭代的初始解其中，d（ I,j ）＜Pbest（j），则进行上述交叉操作，否则进行自身变异；

（4）得到当前迭代次数下的适应值。

输出：Gbest及路径

3 最短路径优化

3.1 常规路径优化

根据描绘的实际位置分别做出A、B、C三个配送点到需求点的赋权（无向）图，如图3所示。

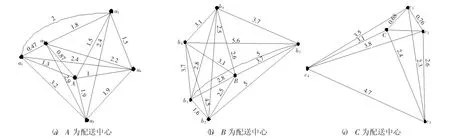
图3 以A、B、C为配送点到各需求点的赋权图

运用Lingo11软件求解以A、B、C点为配送中心的最短配送距离：以A点为中心1.5km范围内的最短配送距离为8.64km，配送路径为A→a5→a4→a3→a1→a2；以B点为中心3km范围内的最短配送距离为18.3km，配送路径为B→b2→b1→b4→b5→b3；以C点为中心2.2km范围内的最短配送距离为11.77km，配送路径为C→c4→c3→c1→c2。

由农场到全部需求配送点的最短距离为91.91km，配送路径为RH→a1→a2→A→a4→a3→b4→b5→B→b3→b2→b1→C→c2→c1→c3→c4→a5→RH。

3.2 基于改进离散粒子群的路径优化

3.2.1 以A、B、C为配送中心的路径优化

将各配送点的相对坐标导入，通过MATLAB2016得到ACPSO改进粒子群算法与2SGPSO改进粒子群算法的收敛曲线如图4、图5所示。

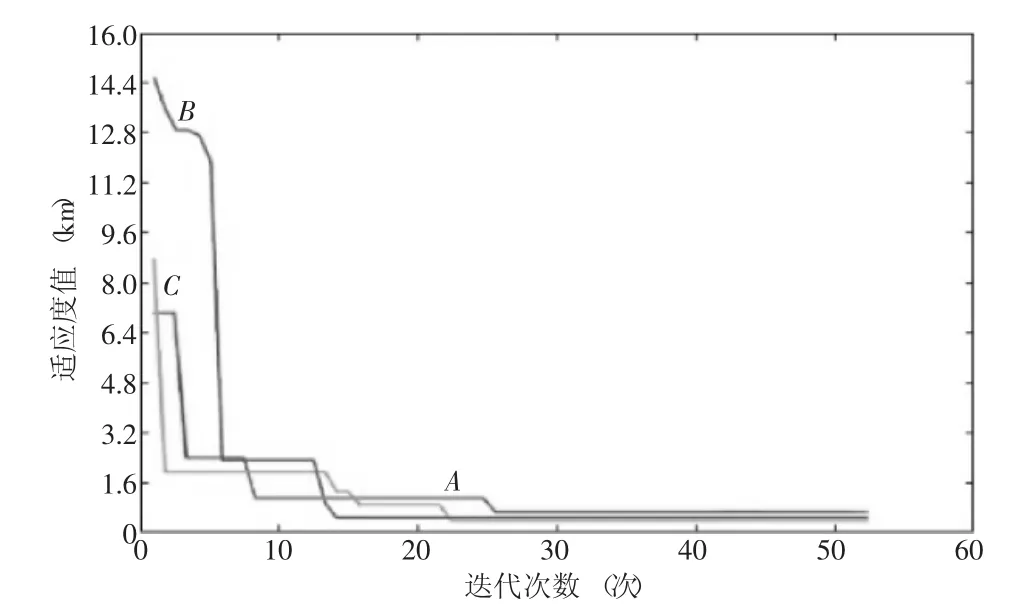
图4 ACPSO算法的收敛曲线

图5 2SGPSO算法的收敛曲线

表1、表2统计了两种算法的运行结果，可以发现：ACPSO改进粒子群算法软件运行结果显示收敛效果较好，较快。迭代30次以后，即趋于稳定；2SGPSO改进粒子群算法软件运行结果显示收敛速度较慢，容易形成局部最优。

表2 2SGPSO算法运行结果

综合两种改进粒子群算法以及常规路径优化结果，ACPSO算法求得的以A、B、C三个配送点为起点配送路径长度最优：A→a2→a1→a3→a4→a5，最短路径为 6.74km；B→b2→b1→b4→b5→b3，最短路径为 14.6km；C→c1→c2→c3→c4，最短路径为8.74km，如图6所示。2SGPSO改进算法中获取最优目标函数过程波动较小，收敛运算速度快，针对优化对象数量较小的模型，效果一般。

图6 ACPSO算法优化的以A、B、C为配送点的最优路径图

3.2.2 以农场为配送中心的路径优化

将全部配送点坐标代入两种改进算法中，再次求解取消配送点的情况下，由农场直接配送到各个需求点的全局路径，结果如表3所示。

表3 全局路径的运行结果

图7 两种算法求解全局路径的收敛曲线图

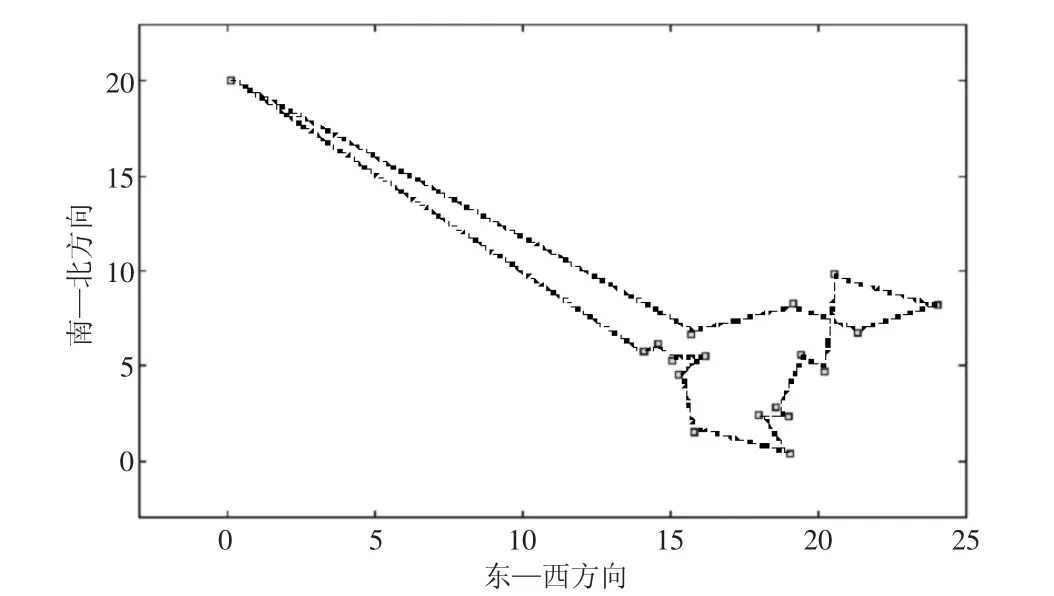
图8 2SGPSO算法的全最优路径

如图7，从全路径优化来看，2SGPSO求解全部路径收敛速度快，收敛效果好，在迭代40～50前后趋于稳定。2SGPSO算法求解的最优路径的路径如图8所示。全局配送最短路径为：RH→a1→b4→B→b3→b5→b2→b1→c1→c2→C→c3→c4→a5→a4→A→a2→a1→RH，最短路径为85.01km。

4 结论

本文介绍了ACPSO算法与2SGPSO算法在RH农场生鲜农产品物流路径设计优化中的应用，结合运行MATLAB软件得出以A、B、C为起始配送点的最短配送路径以及由农场直接配送的最短配送路径。ACPSO算法更加适合小范围内最优路径设计，ACPSO算法得到的最优值明显优于2SGPSO算法；2SGPSO算法下的收敛速度较快，多次迭代后趋于稳定，更加适合进行数量较多的配送点的路径设计优化。