基于Monte-Carlo的岩体三维裂隙网络模型研究
张 亚,彭乐文
(河海大学地球科学与工程学院,江苏 南京 211100)
Monte-Carlo随机模拟技术是通过一定的随机数生成方法,生成服从某一随机变量的概率分布形式的随机数序列。由于裂隙的分布具有很大的随机性、不确定性,可以把裂隙几何参数当作一种随机变量,并且大量研究表明裂隙几何参数的分布服从一定概率分布形式,因此可以将Monte-Carlo随机模拟技术运用到裂隙岩体中来研究裂隙分布特征以及裂隙网络模型。离散裂隙网络(DFN,discrete fracture network)将岩体切割成很多由相邻结构面接触而组合的块体,块体的变形及运动均由结构面控制,并且裂隙网络为地下水流唯一的渗流通道。对裂隙岩体来说,离散裂隙网络模型比等效连续介质模型更能刻画地下水实际的渗流情况[1]。
随着计算机技术的发展,随机裂隙网络的模拟也成为当今研究的热点之一。王晋丽等[2]利用Monte-Carlo随机模拟技术生成二维裂隙网络渗流模型,研究了裂隙网络中水流在不同边界条件下的流动特征;李新强等[3]根据结构面的分布特征利用计算机模拟技术建立了裂隙网络模型,并对该模型进行了等效岩体渗透张量的求解;张彦洪等[4]通过人工模拟方法建立随机裂隙网络模型,研究了裂隙开度和渗透压力对裂隙岩体渗流应力耦合特性的影响。在有限的地质测量基础上,冯学敏等[5]运用Monte-Carlo方法建立了与实际岩体裂隙同分布的随机裂隙网络;敖雪菲等[6]在研究坝基裂隙岩体灌浆时,基于Monte-Carlo方法建立了裂隙岩体三维网络模型,结果表明该法能有效反应裂隙真实特征并获得贴近实际的灌浆结果;刘日成等[7]通过随机模拟技术建立了2种DFN模型,考虑2种边界条件研究了DFN的非线性渗流特征;刘泉声等[8]基于裂隙网络模拟技术Monte-Carlo法,通过Fish语言编制DFN模型生成程序DFN-GEN,研究了应力对等效渗透系数的影响。DFN建模技术应用领域比较广泛,不仅在裂隙岩体渗流方面得到应用,而且郎晓玲等[9]、刘广峰等[10]也将DFN模型建模技术运用到了油田开发等方面。
根据大量的实践经验,可以发现裂隙分布非常复杂,并且裂隙几何参数难以确定,但许多研究表明在裂隙网络模拟中假设结构面为薄圆盘形状是比较符合实际情况的[11]。因此,研究利用Monte-Carlo随机模拟技术建立裂隙为薄圆盘形状的三维裂隙网络模型,并对模型进行验证、统计窗裂隙交线分析以及裂隙网络连通率计算。
1 Monte-Carlo随机模拟原理
Monte-Carlo随机模拟方法的基本原理是利用[0,1]区间标准均分随机数,根据由已知裂隙几何参数的密度分布函数求得的抽样公式来获得服从给定裂隙几何参数分布形式的随机变量。
1.1 标准均匀分布随机数的产生
目前,在工程应用中多运用数学方法通过计算机编程来产生所要的随机数。同余法是产生标准均匀分布随机数最为常用的数学方法之一,它包括乘法线性同余法、混合线性同余法、二次同余法和加法同余法(见表1),其中研究使用的是混合线性同余法。

表1 常用的同余法
1.2 标准均匀分布随机数检验
随机数检验是对利用随机数生成器产生的伪随机数序列与真正的[0,1]均匀分布随机数序列相似程度的检验。常用的检验方法包括:参数检验、均匀性检验、独立性检验等,其中均匀性检验又包括χ2检验和K-S检验。统计检验不能完全肯定或否定某一假设,最好能够多做几种统计检验,以便有较大的把握保证使用的随机数列有较好的统计性质。研究所用的随机数检验方法如下:
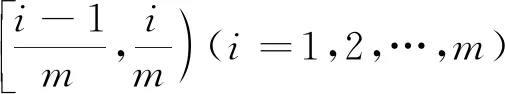
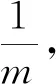
(1)
该统计量公式渐近地服从χ2(m-1) ,通过查χ2分布表,即可对频率差异性做显著性检验。
(2) 独立性检验 独立性检验是检验一组随机数相互之间是否存在相关性。设u1,u2,…,ui为一组按先后顺序排列的随机数序列,前后距离为k的随机数相关系数为
(2)
因此,统计量为
(3)
当在n充分大时,Vk近似服从N(0,1)分布。
1.3 随机变量抽样
在Monte-Carlo随机模拟中,随机变量是通过在标准均匀分布随机数的基础上经过一定的概率分布函数公式变换处理得到的,并且服从不同分布形式,这一过程称为随机变量抽样。抽样的方法主要包括:直接抽样法(又称反函数法)、复合抽样法、舍选抽样法和变换抽样法等,其中直接抽样法最为常用和有效。
直接抽样法的基本思路为:设随机变量t服从分布p(t),累积分布函数P(t),则P(t)的值域为[0,1],所以可以均匀分布随机数ui作为P(ti)的函数值。根据累积分布函数与分布函数的关系,在P(ti)和ui之间建立t与u对应关系:

(4)
求式(4)的反函数得
t=p-1(u),
(5)
将p(t)代入式(4),再将式(4)代入求反函数之后的式(5),即可得到抽样表达式。几种常见分布形式的抽样表达式如表2所列。

表2 常见分布的抽样表达式
2 结构面分布规律及几何特征
2.1 结构面分布规律
虽然结构面的发育具有随机性,但是同组结构面在岩体内分布具有一定的规律可循,即结构面具有等距性和韵律性。结构面的分布规律不仅为研究岩体结构力学和岩体水力学模型提供了依据,还有助于研究结构面的力学特性。
结构面的等距性是指同组结构面在一定尺度上、一定范围内具有相同的间距。无论是大尺度还是小尺度,这种等距现象都存在。结构面的等距性主要受以下4种因素的影响:岩石力学性质、应力强度、构造作用和岩层厚度。除了等距性,结构面还表现出韵律性,即裂隙发育密集带和稀疏带交替相见出现,且带与带之间具有一定间距。结构面韵律性分布的形成机制一直是学者研究的热点,目前公认的2种理论模式为:饱和模式与传播模式。
2.2 结构面几何特征
裂隙岩体中力学特征及水力特征受裂隙控制,而裂隙的空间分布又可以通过几何特征来表征。结构面的几何特征主要是指结构面的形态以及结构面几何参数,其中结构面几何参数又包括方位、规模、张开度和粗糙度等。
(1) 结构面形状 结构面形状是指在忽略厚度的情况下,在延伸平面上的几个形状。由于地质条件的复杂性,在不同形成条件下、结构面的形状完全不同,很难用一个统一的形状来概括,因此许多学者提出了不同的概念模型,主要包括:正交模型(见图1)、圆盘模型(见图2)和多边形模型等。

图1 结构面正交模型Fig.1 Structural surface orthogonal model

图2 结构面圆盘模型Fig.2 Structural surface disc model
(2) 结构面参数 结构面的几何参数一般包括:产状、间距、迹长、粗糙度、张开度、充填物和连通性等,其中间距是指相邻结构面的垂直距离,用来反映结构面发育的密集程度,另外根据所测的平均间距可将岩体进行描述(见表3);迹长是指结构面与露头面的交线,用来描述和评价结构面的连续性,国际岩石力学学会提出的分级标准见表4;张开度是指裂隙两壁间的垂直距离,是表征渗透性重要的几何参数之一。

表3 结构面间距分级表

表4 结构面连续性分级表
3 裂隙网络模型的建立
3.1 结构面分布的概率分析
裂隙发育具有很大的随机性,即裂隙几何参数具有随机性,属于随机变量,因此可以用相应的概率分布来描述。目前,常见的裂隙几何参数的概率分布函数包括:均匀分布、负指数分布、正态分布和对数正态分布等[12]。
根据大量的野外资料表明,结构面的产状、迹长、间距及张开度等几何要素服从于某种随机分布,其中均匀分布一般适用于产状的分布形式,负指数分布一般适用于迹长、间距和张开度分布形式,如图3所示;正态分布一般适用于产状和迹长分布形式,如图4所示;对数正态分布一般适用于迹长、间距和张开度分布形式。常见的几何要素概率分布规律见表5[13]。

图3 间距的负指数分布形式Fig.3 Negative exponential distribution of spacing
3.2 DFN的建立
野外岩体裂隙分布是复杂的,大量的工程实践证明,裂隙的分布特征服从一定的规律。因此,可以通过野外露头、平洞等裂隙的统计分析,建立裂隙分布的概率模型,并通过Monte-Carlo随机模拟方法,在计算机上建立反映服从该概率分布规律的三维裂隙网络模型。裂隙网络模拟过程是根据现场裂隙统计资料获得裂隙几何参数的概率分布规律,应用Monte-Carlo随机模拟方法,对已知的密度函数进行随机抽样,进而得到与实际分布函数相应的随机变量,进而推算出每条裂隙的空间位置坐标,并结合裂隙几何参数在计算机上生成形象直观的三维裂隙网络。
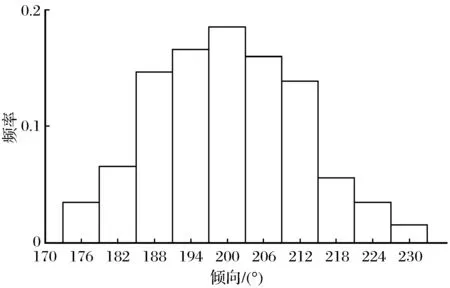
图4 倾向的正态分布形式Fig.4 Normal distribution of tendency
实际上,随机裂隙网络建模的过程就是根据露头得到有限的裂隙信息推求服从这些概率分布特征的岩体内部以及更大区域的裂隙分布,建立能够反映现场实际情况的裂隙网络模型[12]。基本的三维裂隙网络模拟流程如图5所示。
4 实例分析
4.1 工程概况
根据文献[1]中某水电站坝址区裂隙的几何参数统计资料,并结合Monte-Carlo模拟技术建立三维裂隙网络模型。裂隙的几何参数如表6所列,其优势方向为北东向和北西向。对裂隙的几何分布进行拟合,部分拟合结果如图6、图7所示。

表5 结构面几何要素经验概率分布
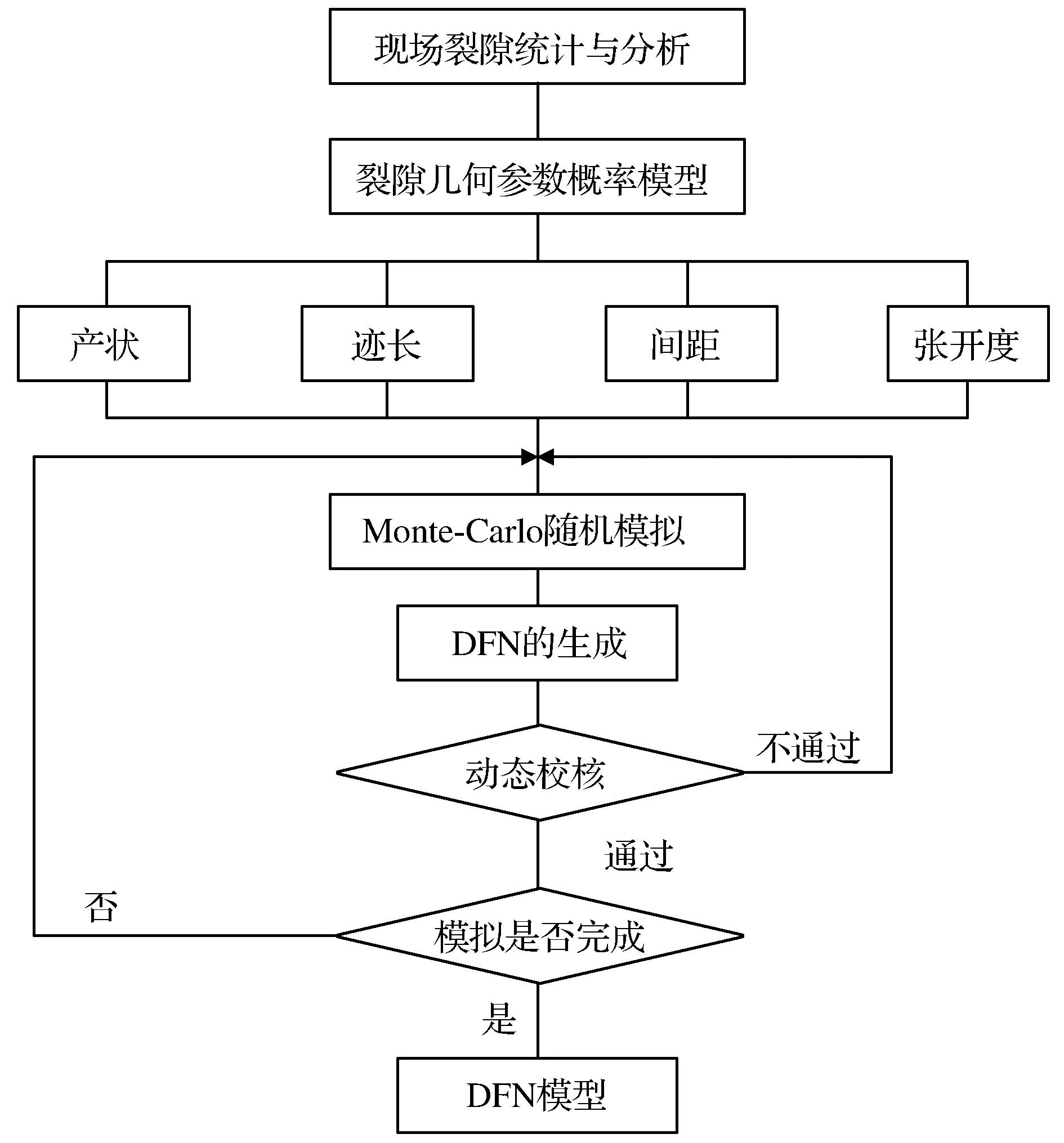
图5 三维裂隙网络模拟流程Fig.5 3D crack network simulation flowchart
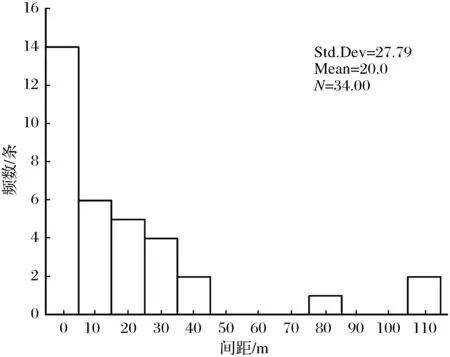
图6 间距(NE)频数直方图(负指数分布)Fig.6 Frequency histogram (Negative exponential distribution) of crack spacing (NE)
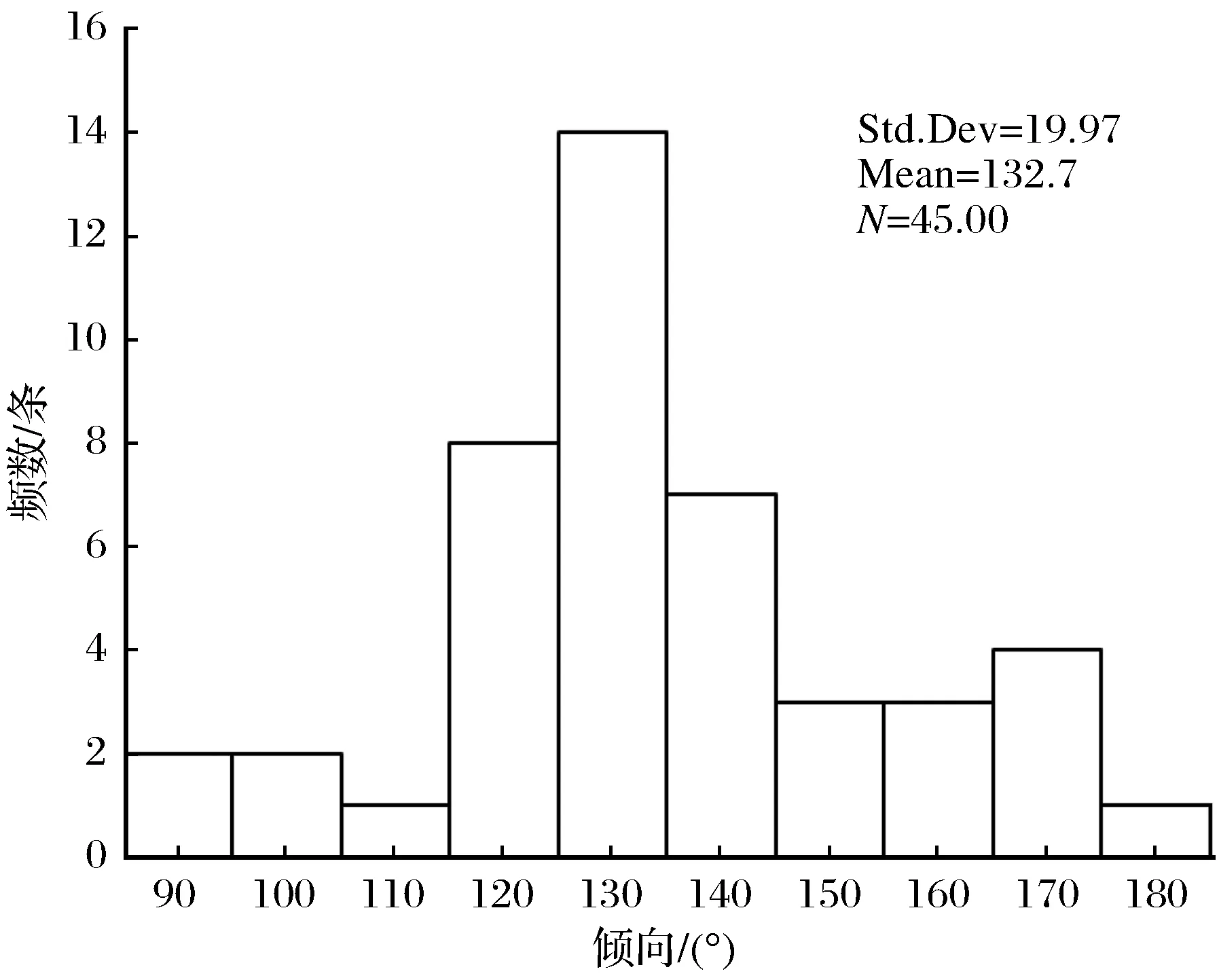
图7 倾向(NE)频数直方图(正态分布)Fig.7 Frequency histogram (Normal distribution) of tendency (NE)
4.2 岩体三维裂隙网络的模拟
设置裂隙生成区域为200×200×200 m3,正北向为X轴,正东向为Y轴,垂直向为Z轴。由于该区域发育2组优势裂隙,故将NE向、NW向分布命名为DFN01和DFN02。2组裂隙的数量大小由结构面体密度控制,而求得所需要生成的2组裂隙数量的方法可参考文献[14]中所述方法,主要思路如下:
由线密度λd和结构面间距d的定义可知两者互为倒数,则有
(6)
(7)
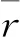
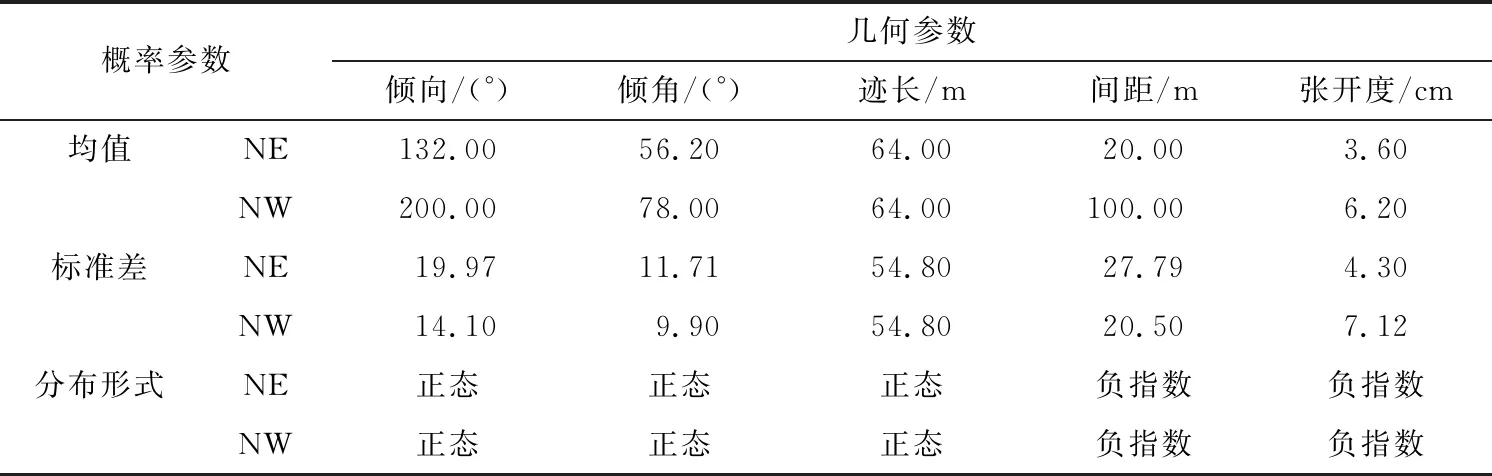
表6 某水电站坝址区裂隙几何参数统计

(8)
因此,模拟区域V内的结构面数量n为
(9)
经计算可知,NE向裂隙组DFN01所需生成裂隙数量为307条,NW向DFN02所需61条,由此生成的三维裂隙网络模型如图8所示,其中DFN01标记为蓝色,DFN02标记为绿色。
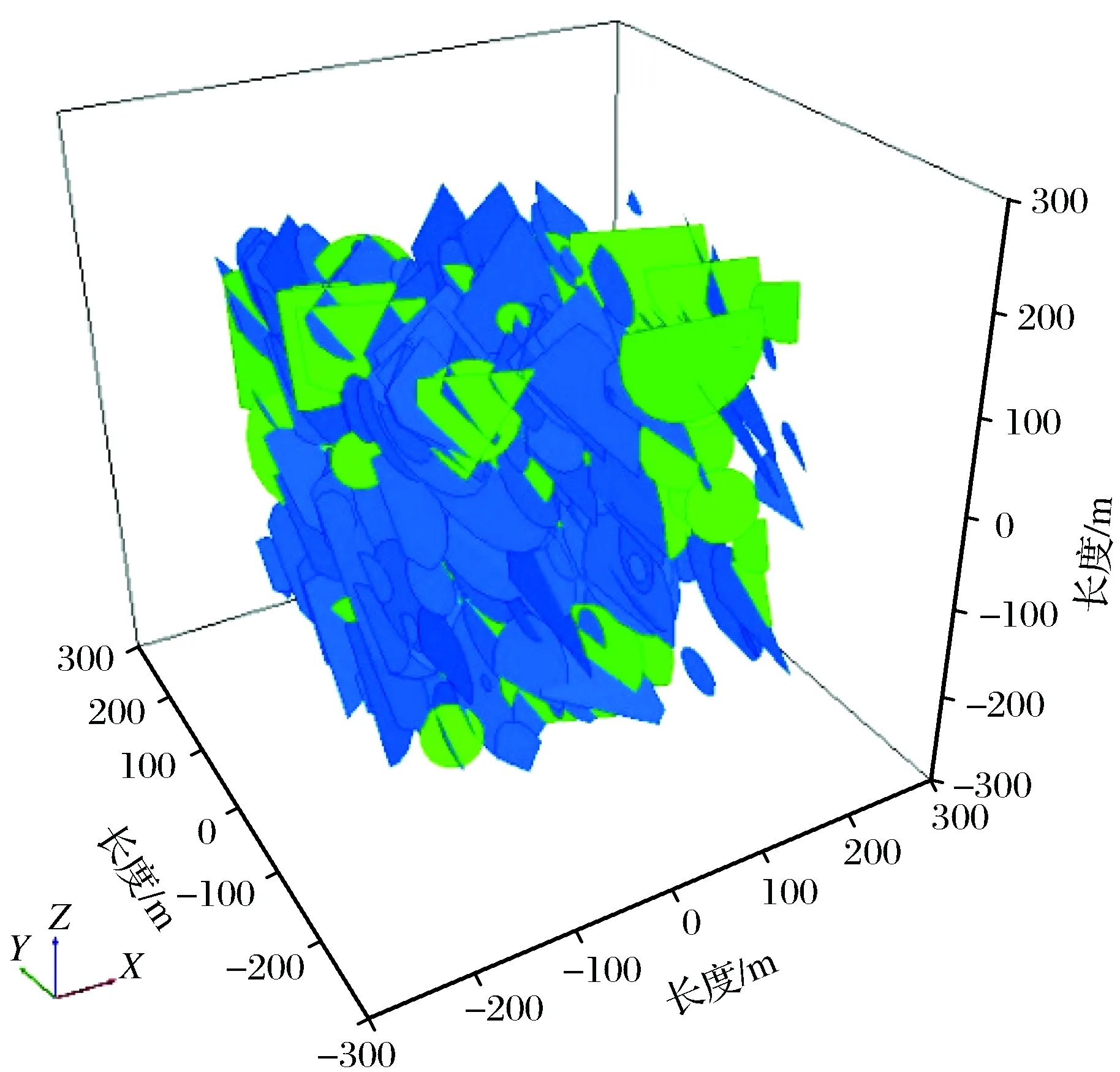
图8 三维裂隙网络模型Fig.8 3D crack network model
4.3 模型的验证与分析
(1) 模型的验证 根据裂隙网络模型求得所生成DFN的几何参数信息,结合现场裂隙统计得到的裂隙几何特征对通过Monte-Carlo随机模拟技术建立的三维裂隙网络进行验证。模型验证一般可以考虑对比模型数据与实测数据之间结构面平均倾角倾向、平均迹长、线密度等参数。在模型中设置4条测线来计算所建DFN的线密度,如图9所示。对比模型数据与实际数据之间线密度的差异性,并计算相对误差百分比,结果见表7。

图9 测线及统计窗布置示意图Fig.9 Measuring line and statistical window layout map
由表7裂隙网络线密度模拟值与实测值对比来看,相对误差百分比均≤10%,认为该模型模拟结果比较贴近实际情况。
(2) 模型分析 研究对模型的分析主要包括统计窗裂隙交线分析和裂隙连通率计算分析。统计窗设置如图9中红色平面所示,统计窗坐标分别为(-200,-200,0)(-200,200,0)(200,200,0)(200,-200,0)。统计窗裂隙交际线如图10所示。统计窗上蓝色裂隙交线为DFN01与统计窗的交线,绿色为DFN02与统计窗的交线。
由图10可知,DFN01和统计窗相交而成的交线与DFN02和统计窗交线的夹角约为70°,这与表6中所示的2组裂隙走向的差值大致一致。DFN裂隙连通率主要是通过裂隙间的交线的长度来反映的,即交线长度越长,裂隙连通率越大,裂隙连通率计算如图11所示。由图11可知,大部分裂隙交线的走向为NE向,这是因为DFN01数量较多,约为DFN02数量的5倍;裂隙连通率较大的交线是2组优势裂隙中半径较大的裂隙相交而形成。
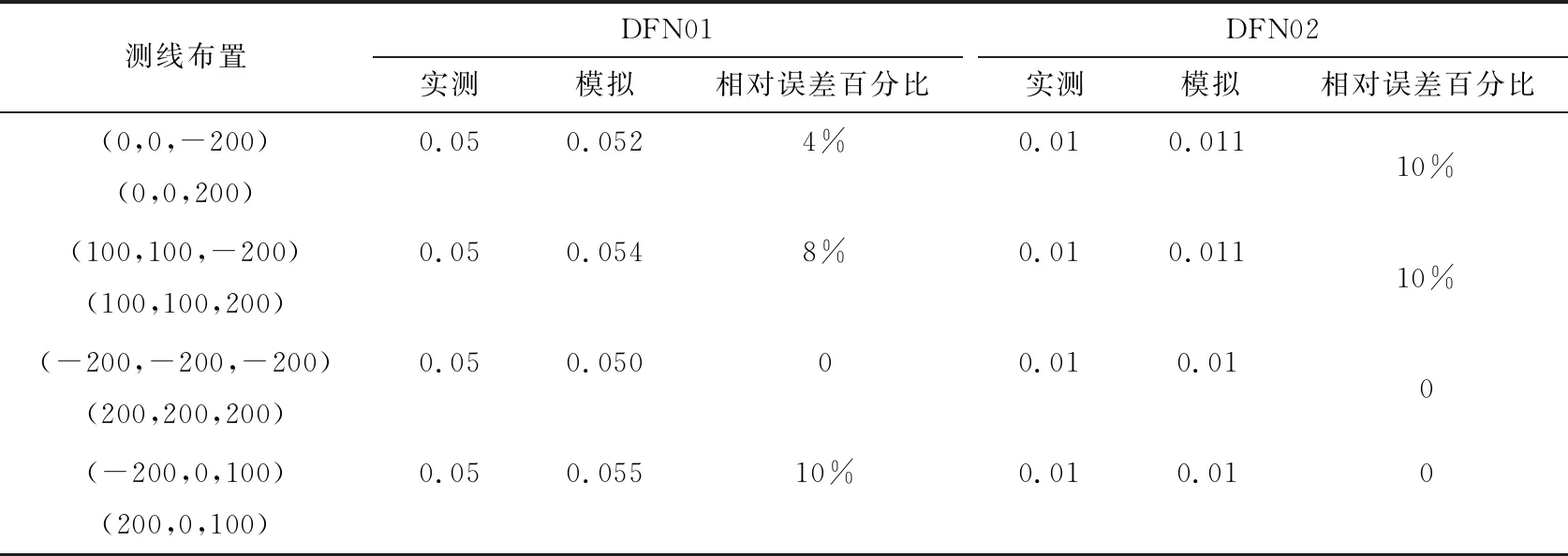
表7 裂隙网络线密度模拟值与实测值对比

图10 统计窗上裂隙交线分布Fig.10 Distribution of the crack intersection on the statistical window
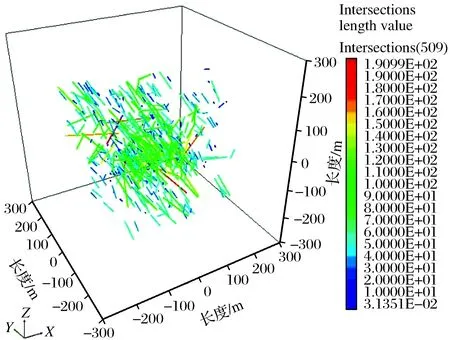
图11 裂隙连通率计算Fig.11 Crack connectivity calculation
5 结语
研究采用Monte-Carlo随机模拟方法建立了三维裂隙网络模型,主要通过混合线性同余法生成随机数,并且对随机数进行χ2检验和独立性检验,结合实测裂隙统计与分析得到的裂隙几何参数概率分布的抽样公式对随机变量进行抽样,得到与实际分布函数相应的随机变量,并且假设结构面为薄圆盘形状,进而建立DFN模型。
在裂隙网络模拟之后,需要进行模型的验证,通过对比实测数据与模拟数据之间的线密度参数的差异性来检验模型的可靠性,验证结果表明模型拟合度较高。建立模型之后,除了对模型统计窗裂隙交线分析和裂隙连通率计算分析,还可以近似地求得RQD、渗透系数张量等参数。利用Monte-Carlo随机模拟技术对三维裂隙网络模型的研究,不仅为裂隙岩体的建模提供了一种很好的思路,并且为后续对裂隙岩体渗流的研究工作提供了技术支持。

