中国股市低风险异象研究
周 亮,王银枝
(1.湖南财政经济学院 财政金融学院,湖南 长沙410205;2.中国人民银行郑州培训学院,河南 郑州450011)
一、引言
低风险异象指的是高Beta 证券的Alpha 往往偏低,这与传统的资产定价模型(CAPM)是相悖的。CAPM 模型的一个基本假设是投资者能够通过任意增减杠杆的方式投资于单位风险下预期超额收益最大(即夏普比率)的投资组合,从而满足他们自身的风险偏好。但是很多投资者,如个人投资者、养老基金和共同基金等,由于受到融资约束,不能自由使用杠杆,因此为了达到特定的收益率目标,只能够选择高Beta 的资产进行投资,从而导致高Beta 的资产价格偏离其内在价值,未来风险调整后收益率就会显著降低;相反,低Beta 资产由于其收益率较低,因此并不被投资人所喜爱,从而导致其价格被低估,未来的风险调整后收益也会相对更高。对内含杠杆的ETF 基金的热衷更是直接证明了大多数投资者并不能直接使用杠杆。这种热衷于高Beta资产的投资行为预示着高Beta 资产相对于低Beta 资产而言,具有更低的风险调整后收益。在我国资本市场上最典型的是债券和股票间的收益差别,目前债券的年化收益率不到4%,但是其年化波动率也不到3%,而沪深300 指数年化收益率超过10%,但是其年化波动率却高于25%(周亮和李红权,2019)[1]。因此综合来看,债券的风险调整后收益更高,但是由于4%的收益率并不能满足绝大部分投资者的要求,而且并不能自由使用杠杆,因此一般投资者仍然倾向于进行股票投资。
为了更准确地对低风险异象进行分析,Frazzini&Pederson(2014)[2]构造了一个Beta 套利策略(以下简称BAB),结果发现在全球20 个股票市场、债券市场及商品期货市场上BAB 套利策略均能获得稳定的盈利,且随着高低Beta资产间的Beta差异越大,收益越高。随后很多学者对BAB 在全球市场的应用情况展开了研究,均支持了低风险异象的存在和有效性,且市场流动性会显著影响到BAB 策略的收益,即低风险异象受市场流动性影响较大。中国资本市场上散户投资者过多,而机构投资者占比相对欧美发达市场偏小,市场投机氛围更重,且由于政府监管更严格,杠杆约束相对于发达资本市场更强,因此有理由相信中国资本市场也存在着显著的低风险异象。但是目前对中国市场低风险异象的研究很少,仅有于谊卉(2016)[3]采用Frazzini & Pederson(2014)[2]的方法对我国股市进行了初步探讨。因此,系统性地研究我国资本市场上的低风险异象具有较强的理论和现实意义,一方面可以为投资者的资产配置及监管者的政策监管提供经验借鉴,另一方面也是对我国资本资产定价理论的完善和补充。
二、文献综述
Jensen et al.(1972)[4]的研究证明了高Beta 股票构成的投资组合相对于低Beta股票构成的投资组合的收益率更低,可以称之为低风险异象。在此之后,Blum 和Friend(1973)[5]、Fama 和Macbeth(1973)[6]、Fama 和French(1992;1993)[7-8]以 及Baker et al.(2011)[9]的研究也证明了低风险异象的存在。Fama和French(1993;2006)[8,10]发现在控制了规模和市值特征(三因子模型)之后,Beta 和收益率之间的关系变得更为单调。Carhart(1997)[11]在三因子模型的基础上增加了动量因子从而构造了四因子模型,Pástor 和Pietro(2003)[12]更是又增加了流动性因子和盈利因子构造了六因子模型,但是这些模型虽然使得模型Alpha 下降,却更证明了低风险异象在股票市场的存在性。Frazzini 和Pederson(2014)[2]通过全球多个股票市场和期货市场的数据验证了高Beta资产的低收益性,他们构造了一个Beta套利策略(以下简称BAB),用来检验低风险异象的大小。即加杠杆买入低Beta 的资产使得其Beta 为1,同时降杠杆卖出高Beta 的资产使得其Beta 也为1,结果发现在全球20 个股票市场、债券市场及商品期货市场上BAB 套利策略均能获得稳定的盈利,且随着高低Beta资产间的Beta差异越大,收益越高。在此之后,大量学者对BAB 策略进行了研究,Novy-Marx(2014)[13]、Auer 和Schuhmacher(2015)[14]、Buchner 和Wagner(2016)[15]、Abdollahi et al(2017)[16]的研究结论均支持了BAB 能够获得稳定盈利的结论。许多学者从行为金融学视角来对这种现象进行解释,如Jensen et al(1972)[4]从杠杆限制的角度、Baker et al(2011)[9]从市场基准追踪的角度分析了市场分割导致的低风险异象。Bali et al(2014)[17]的彩票需求心理理论也可以对这种异象进行解释。
我国学者在资产定价方面的研究,主要还是集中在对CAPM 模型及风险因子定价模型的研究上。在CAPM 模型的研究方面,田丁石和肖俊超(2012)[18]研究发现在历史贝塔值分组条件下,沪深股市基本符合CAPM 模型。但是李和金和李湛(2000)[19]却发现上海股市系统性风险与收益存在正相关关系,但并不是CAPM 所预料的线性关系。陈学信(2018)[20]对CAPM 模型进行了详细总结,并探讨了多种CAPM 模型间的差异,进而提出了基于价格错定的HCAPM 模型。在风险因子定价模型方面,陈守东、孟庆顺和赵云立(2003)[21]较早对FF 三因子模型进行了研究,利用最小二乘法和广义距估计方法(GMM)研究了上证180 指数样本股和深证100 指数样本股,结果表明三因子模型对于中国股市是基本适用的。周亮(2017)[22]对中小板股票的研究,发现流动性因子和盈利因子能够显著提升多因子模型的解释效力。干伟明和张涤新(2018)[23]在FF 三因子模型的基础上增加了盈利因子、成长速度因子和成长质量因子,发现扩展后的模型明显增强了解释力。对于股票Beta 的研究,国内学者主要集中于对Beta 自身时变性或随机性的研究(罗捷和劳兰珺,2008;徐建卫,2015)[24-25],对于低风险异象的研究极为少见,目前仅有于谊卉(2016)[3]采用Frazzini和Pederson(2014)[2]的方法对我国股市进行了初步探讨,验证了BAB 策略在我国的有效性。但是于谊卉(2016)[3]只是对BAB 策略的盈利能力进行分析,并没有区分不同市场状况下低风险异象的差异性,也没有分析资金约束对低风险异象的影响。基于此,本文将系统性地对我国资本市场上的低风险异象进行详细分析,首先借鉴Frazzini和Pederson(2014)[2]的研究方法,通过构造BAB 因子研究我国股票市场的低风险异象,通过牛市、熊市的划分,研究不同市况下低风险异象的差异以及稳健性;然后,通过对市场流动性的分析来判断资金约束对低风险异象的影响,以深入探讨低风险异象产生的机制;最后,本文还初步探讨了商品期货市场低风险异象的存在性。
三、数据与方法
(一)Beta的计算方法
采用我国股市数据来对我国资本市场的低风险异象进行检验。首先需计算个股的Beta,计算公式如式(1)所示:


其中,wi为修正系数为横截面平均Beta 值。借鉴Frazzini 和Pederson(2014)[2]的处理方式,设定相对于采用原始Beta 数据直接计算,这种处理方式对最终结果的影响不大(Frazzini &Pederson,2014)[2]。
(二)BAB因子的构建方法
通过构造BAB 因子来检验我国股市中的低风险异象,即买入低Beta 股票的同时卖出高Beta 的股票,具体步骤如下。
第一,将所有股票按照Beta 从低到高的顺序进行排序,选出排序最低的1/4 股票为低Beta 组,选择排序最高的1/4股票为高Beta组。
第二,按排序对高低Beta 组中的每个股票赋予不同权重,使得在低Beta 组中Beta 越低的股票权重越高,在高Beta 组中Beta 越高的股票权重越高。设由zi=rank(βit)构成的z为Beta排序的n×1阶向量为低Beta 组中最大的Beta 对应的顺序,zH
min为高Beta组中最小的Beta对应的顺序,则:

其中,wL、wH分别为低Beta 组股票和高Beta 组股票对应的权重向量为高低Beta 组Beta 排序和的倒数为n×1 阶单位向量。通过这种赋权方式,使得
第三,构造最终的BAB因子:
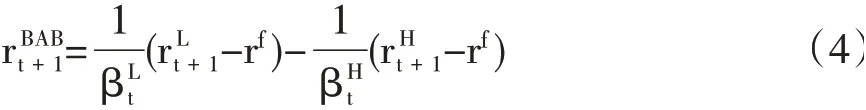
通过以上三步就可以构造出市场中性的BAB因子,用来研究我国资本市场的低风险异象。
(三)数据来源及描述性统计
为了保证样本数据足够多,选取了2002 年以前上市的A 股公司作为研究对象,剔除掉已退市及数据不完整的公司,共得到958 家公司数据。选取所有公司2002年1月1日至2018年5月31日所有的日收盘价数据(复权后)作为分析对象,对于部分缺失的数据,采用线性插值法补齐。同时考虑到沪深300 指数在2005 年才推出,因此采用上证综指作为市场基准指数,同时采用一年期定期存款利率作为市场无风险利率。需要说明的是,日数据只是用来计算Beta,在研究BAB因子收益时,采用的是月度数据,即用每个月月末时点算出的Beta为研究对象,然后每月进行轮动,同时对于区间的收益也采用月度收益率来衡量。由于计算Beta 需要用到三年的数据,因此虽然全体样本是自2002 年开始,但是在描述性统计及后面的实证检验中,计量数据实际是从2005年1月1日开始。表1报告了个股、市场基准的月度收益率以及个股Beta 的描述性统计情况,可以看到,个股收益率及Beta的极端值都比较大,如个股月收益率最大值达到1341%,Beta 最大值为3.476,而最小值为-1.966;但是从5%和95%分位数来看则显得合理很多,如个股收益率5%和95%分位数分别为-20.7%和26.9%,Beta值的5%和95%分位值分别为0.674和1.48,因此在进行实证分析时剔除掉极端值的影响是很有必要的。需要说明的是,表1 中所有股票Beta 的平均值为1.07、中位值为1.058,并不是1,主要是因为我们选择的市场基准是上证综指,而样本股并没有包含所有的上市公司,因此样本股的平均Beta并没有和市场基准完全一致。但是由于我们在构造BAB 因子时使用的是最高的1/4 和最低的1/4股票数据,中间大部分与市场走势接近的个股已被剔除,因此对结果不会产生影响。

表1 收益率及Beta的描述性统计情况
四、实证检验
(一)Beta与Alpha间的关系
按照Beta 从低到高的顺序将所有股票分成10组,通过统计这10 个组的超额收益、Alpha 和夏普比率等数据,可以观察我国股市中的低风险异象,结果如表2 所示。其中超额收益指对应Beta 组超过市场无风险收益的月收益;CAPM Alpha 指采用CAPM 模型计算出的截距项;三因子Alpha 指采用FF 三因子模型(包括市场因子、规模因子及估值因子,数据从锐思数据库获得)回归得到的截距项;Beta 值对应Beta 组的平均Beta 值;波动率是对应的年度波动率数据,通过月波动率换算而来;夏普比率也是年度数据,通过将超额收益进行年度变换而得到。从表中数据可以看到,CAPM Alpha、三因子Alpha 及夏普比率均呈明显的下降趋势,说明高Beta 对应了低Alpha。从波动率来看,10 个组别之间没有明显差别。图1 和图2 更直观地展示了三因子Alpha 及夏普比率的趋势变动图,可以很明显地看到,从低Beta组开始到高Beta 组,三因子Alpha 和夏普比率均呈现明显的下降趋势。BAB 因子能够获得显著的正收益,低风险异象在我国股票市场是存在的,且BAB 因子的波动率只有0.15,远低于各个组别的波动率,因此夏普比率达到了0.89。Beta 套利(BAB)因子可以产生显著为正的风险调整后收益。
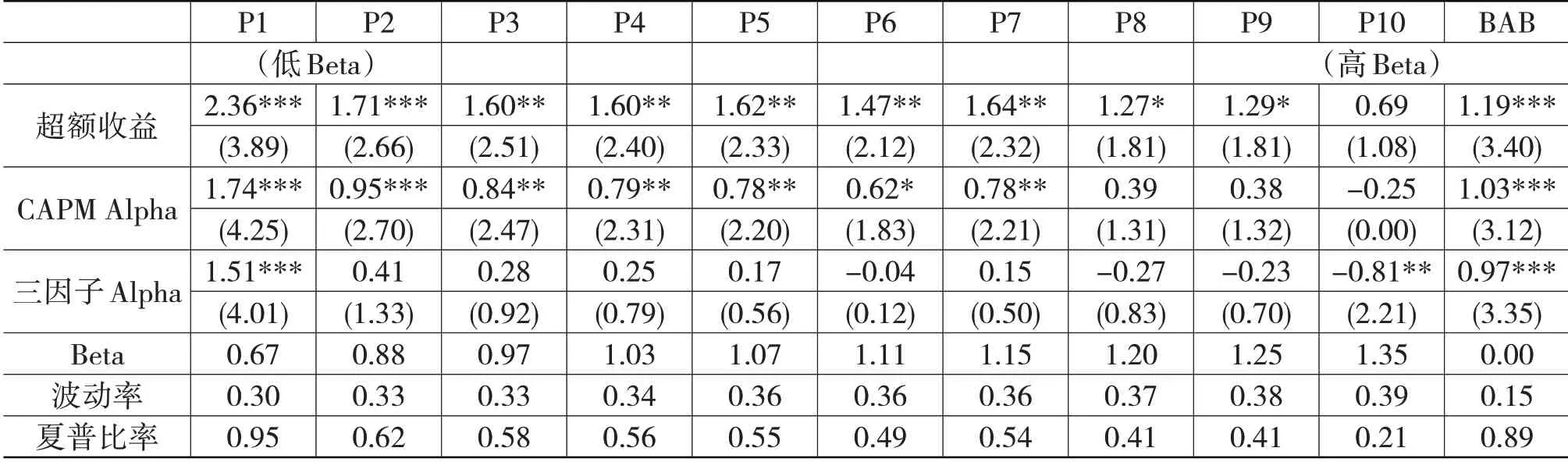
表2 最后一列报告了BAB 因子的统计检验情况,可以看到,BAB 因子在样本区间内获得了1.19%的月度超额收益,控制了市场因子影响后的CAPM Alpha 为1.03%,控制了三因子影响后的三因子Alpha为0.97%,且所有数据均在1%水平下显著,说明
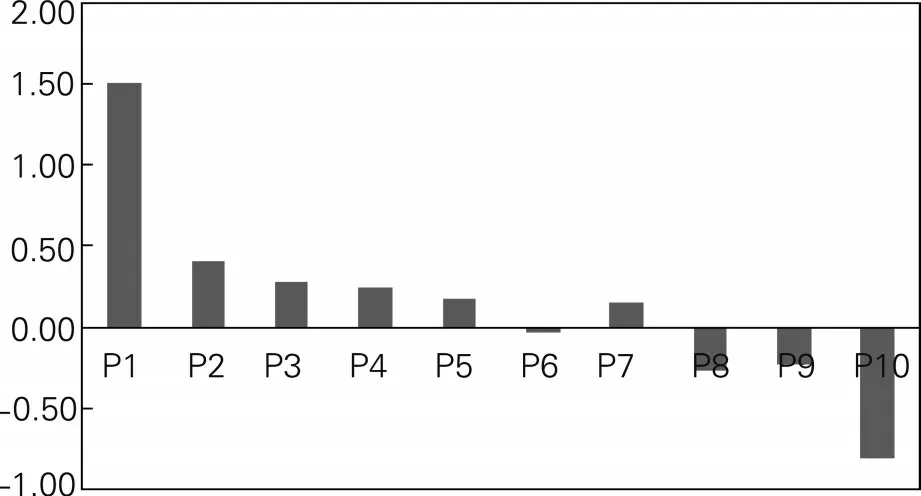
图1 Beta分组的三因子Alpha
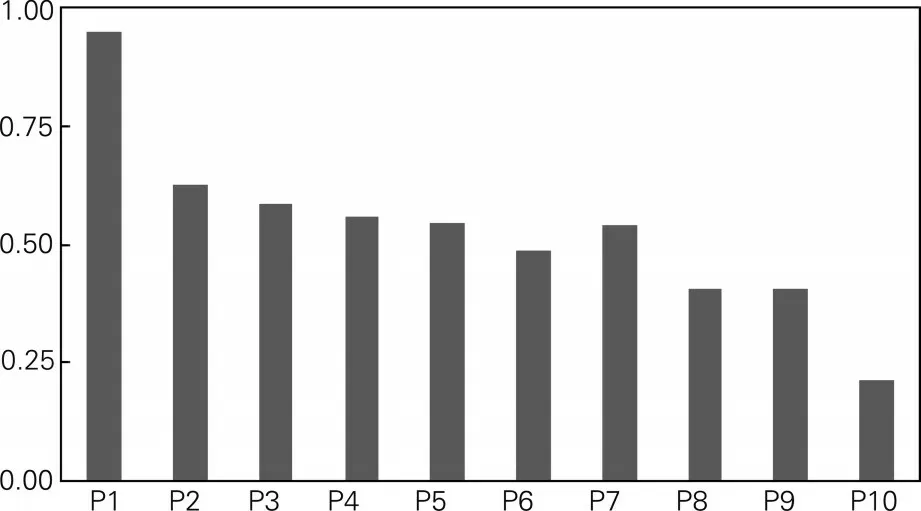
图2 Beta分组的夏普比率
(二)稳健性检验:牛市、熊市是否对低风险异象有影响
通过将市场分为牛市和熊市,既可以分析不同市场状态下低风险异象的差异,同时也可以提供稳健性检验。借鉴Cooper et al(2004)[29]的方法,取上证综指前36 个月的收益率平均值作为标准,若当月收益率大于该值称之为牛市状态,反之则称之为熊市状态,并对牛市和熊市下Beta 分组及BAB 因子的收益及风险情况进行统计,结果如表3 所示。可以看到,在牛市中所有分组的收益均要远超熊市,最低的夏普比率都高达2.79,而熊市中最高的夏普比率为-1.86;但是可以看到,无论在牛市还是熊市,CAPM Alpha、三因子Alpha 及夏普比率均随着Beta的升高而降低。图3 报告了牛市和熊市中不同Beta分组的三因子Alpha,可以清晰地看到,两种市场状态下,Alpha 均随着Beta 的升高而下降。从表3 最后一列可以看到,无论是牛市还是熊市,BAB因子均能获得显著的超额收益,且无论是控制了市场因子的CAPM Alpha,还是控制了FF 三因子的Alpha,均显著为正,两种市场状态下的夏普比率均在0.9 以上,充分说明了无论何种市场状态下,BAB 都能获得稳定的正收益。因此综合来看,我国股票市场上低风险异象是显著存在的,而且结果是稳健的。
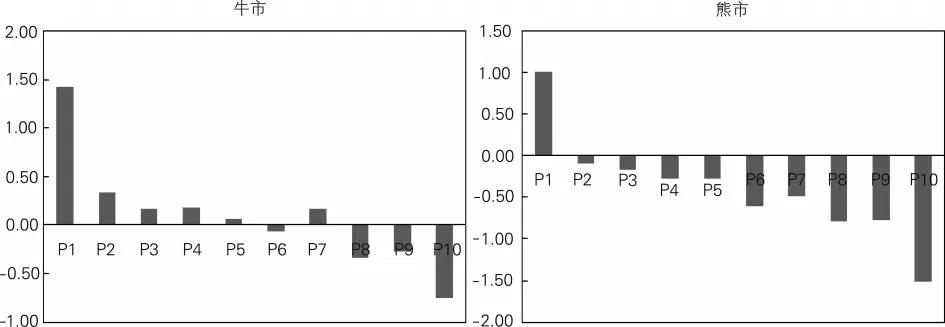
图3 牛市、熊市下Beta分组的三因子Alpha
(三)流动性风险的影响分析
1.流动性风险对Beta截面差异的影响
为了验证假设3,采用Shibor利率的月波动率来衡量市场流动性风险,波动率越高时市场流动性风险越高,反之亦然。采用Parkinson(1980)[30]定义的极差波动率来计算,公式为其中hi和li分别为Shibor 利率在一个月内的最高价和最低价。按照极差波动率的高低,将市场平均分为低流动性风险、中流动性风险及高流动性风险三组。采用标准差、平均离差及组内极差三种方式来衡量Beta的截面差异,其中,平均离差为截面上所有个股Beta 相对于截面均值的偏离程度,计算公式为MD=组内极差为截面个股Beta 上1/5 分位值减去下1/5 分位值的差值。表4 报告了不同流动性风险时期三种截面差异的统计结果,可以看到,在整个样本区间内,Beta 的截面标准差均值为0.149、平均离差均值为0.155、组内极差为0.305;但是在P1(低流动性风险)时期三者的均值分别为0.155、0.168 和0.338,均要高于P3(高流动性风险)时期的0.137、0.138 和0.263;通过P3-P1 项的T 检验,可以看到所有的差值在1%的水平下都是显著的。综上可以发现,提高资金流动性风险,证券间Beta值的差异将减小。
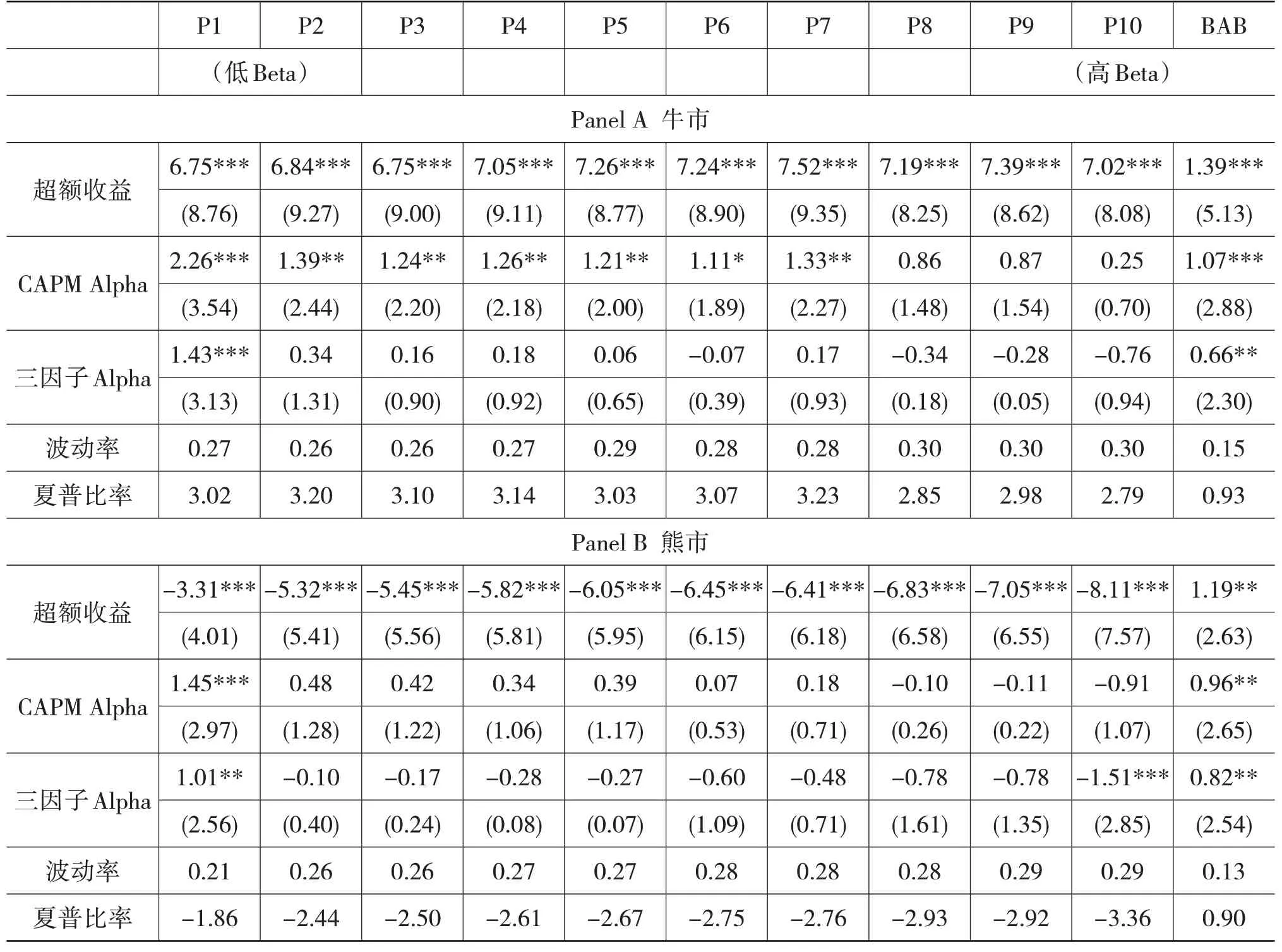
表3 牛市、熊市下Beta分组及BAB因子的收益率统计
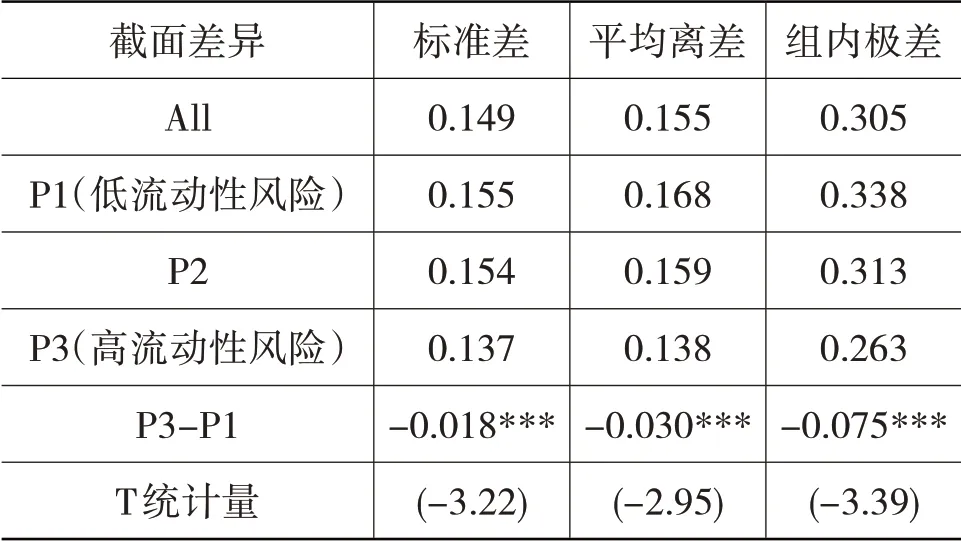
表4 不同流动性风险状况下Beta截面差异的统计结果
2.流动性风险对BAB因子市场敏感性的影响
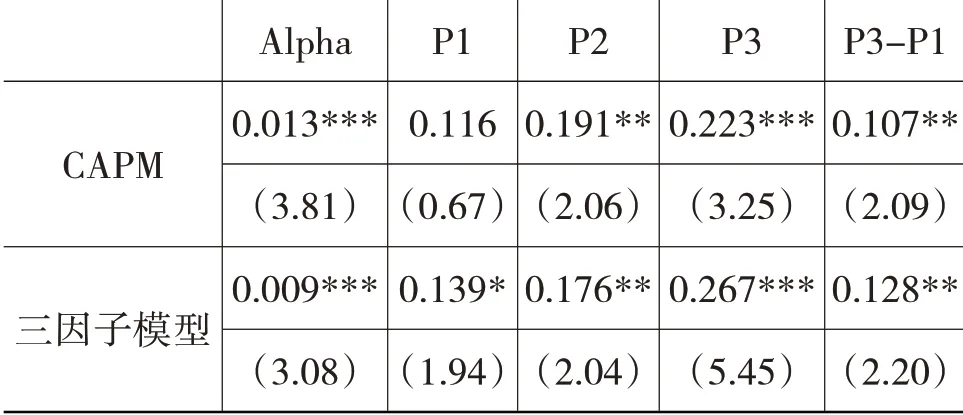
表5 BAB因子收益市场敏感性回归结果
将三种流动性风险状态设置为三个虚拟变量P1、P2、P3,分别表示低流动性风险、中流动性风险和高流动性风险,将三个虚拟变量与市场因子的交乘项代替原市场因子进入CAPM 模型或三因子模型,以分析不同流动性风险时期BAB 因子的市场敏感性。表5 报告了相关回归结果,表中只列出了截距项Alpha 及三个交乘项的回归系数,三因子模型的SMB 和HML 因子的回归系数未列出。从回归结果可以看到,P1 交乘项的回归系数在CAPM 模型中不显著,在三因子模型中只在10%水平下显著,且数值都要低于P3 交乘项的回归系数(在1%水平下显著);最后一列报告了两个系数间差值的检验结果,可以看到高流动性风险时期的系数在5%的显著性水平下要高于低流动性风险时期(分别为0.107和0.128),因此说明流动性风险提高时,BAB 因子的市场敏感性增加。
(四)进一步讨论:商品期货市场是否也存在低风险异象
除了股市以外,我们也尝试考察其他资产市场低风险异象的存在性。由于我国债券市场品种不齐全,数据缺失比较严重,因此选择数据较为齐全的商品期货市场作为研究对象。为了保证样本覆盖的商品品种较多,同时又兼顾数据样本时间足够长,选择2009 年5 月作为研究起点,在此之前共上市了20 个期货品种。由于计算Beta 需要用到3 年的历史数据,因此低风险异象的实际分析时间为2012 年5 月至2018 年5 月。采用风险平价方法(即使得每种商品期货的波动率相同)构造市场基准,一年期定期存款利率为无风险利率。图4 报告了CAPM 模型计算的Alpha 变动情况,其中P1 为最低Beta 组、P4 为最高Beta组。从图中可以看到,商品期货市场的Alpha随着Beta 的增加并没有明显的变化趋势,这可能是由于样本量过小的原因所导致的,相对于股市958家公司的样本宽度,20 个商品期货的样本显得很不足。但是从分析结果初步来看,在我国商品期货市场上低风险异象是不存在的。
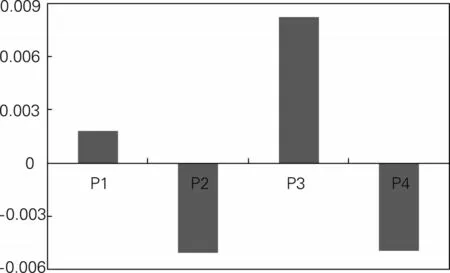
图4 商品期货市场的Alpha变动情况
五、结论与启示
为检验我国股市中的低风险异象,在理论推导的基础上,选取2002 年1 月至2018 年5 月958 家上市公司的日数据进行了分析。实证结果显示:第一,按照Beta 由低到高的顺序进行分组并分析其Alpha及夏普比率的变动情况,发现高Beta伴随着低Alpha的现象在我国股市是明显存在的,且无论牛市还是熊市,结论都是稳健的;第二,通过构建BAB 因子检验低风险异象的大小,并测算其在样本区间的收益情况,发现BAB 因子能够获得显著的超额收益,且在控制了CAPM 市场因子和FF 三因子之后,BAB 因子的Alpha 收益仍是显著为正的,充分说明了我国股市中存在着显著的低风险异象,且无法由传统的风险定价因子所解释;第三,用Shibor利率的波动率来衡量市场流动性风险,结果发现,当流动性风险升高时,个股Beta的截面差异将缩小,也就是说大部分个股的Beta 将趋向于1,且流动性风险的增加会导致BAB 因子收益的市场敏感性增加。因此综合来看,与Frazzini 和Pederson(2014)[2]的结论一致,我们在中国股市上也验证了低风险异象的存在。除此以外,我们还对商品期货市场进行了初步分析,但是研究结论却并不支持低风险异象存在。
低风险异象近年来受到了国外学者越来越广泛的关注,尤其是Frazzini 和Pederson(2014)[2]构建了BAB 因子以来,大量文献对BAB 因子的有效性及不同条件下的表现进行了研究,但是我国学者目前对这方面的研究还有所欠缺。本研究发现在我国股市中这种低风险异象也是显著存在的,该研究结论对于我国资本资产定价理论的完善和发展具有一定的理论价值,同时也对投资实践者和市场监管者具有一定的经验借鉴意义。第一,投资者在实际投资过程中可以有效利用低风险异象,在投资组合中减少风险过高的股票或其他证券产品,并适当增加风险较低的证券进行投资,虽然会摊薄投资收益,但是能够极大地降低投资风险;第二,由于普通投资者面临着较强的融资约束,如果想获得较高的收益,必然只能多投资于高风险的资产,证券公司可以利用自身的资金和渠道优势,针对性地开发新的金融产品,在金融产品中可以适当增加低风险资产的杠杆比率,并降低高风险资产的配置比率,这样既丰富了资本市场的投资产品,也可以扩大证券公司的收益率和影响力;第三,在保证不发生系统性金融风险的前提下,监管层可以适当放松低风险资产的投资门槛以及融资约束,这一方面可以有效引导市场资金进入低风险资产,同时也可以提高资本市场的有效性及资源配置效率。
——基于三元VAR-GARCH-BEEK模型的分析

