WEC-透空式防波堤集成装置能量转换效率研究

毛艳军马小舟

(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连166024)

在可再生能源的开发探索中,波浪能发电装置(Wave Energy Converter,WEC)得到了广泛的研究和应用,但也面临着建设成本较高的问题。针对这一问题,近些年相关学者提出了成本共享的思路,将波浪能发电装置与现有海上结构物集成,一方面可以降低建设成本,另一方面也可以增加装置的稳定性。其中将波浪能发电装置与近岸防波堤进行集成具有较高的可行性和适用性[1-3],此类集成装置的设计方案可应用于现有防波堤的改造以及新型防波堤的结构概念设计。He和Huang[4]将振荡水柱式波浪能转换(Oscillating Water Column,OWC)装置与浮式防波堤进行集成并进行了实验研究,结果显示装置在一定条件下可以获得较好的能量捕获效率和消波效果。宁德志等[1]对一个由垂荡浮子式波浪能发电装置(Heave Oscillating Buny,HOB)与有桩柱约束的浮式防波堤组成的集成系统进行了实验研究,在合适的波频范围和PTO(Power Take Off)系统阻尼条件下可以获得较高的能量捕获率和较好的消波效果。针对此类形式,赵玄烈等分别针对波浪能发电装置集成于有桩柱约束的浮式防波堤[2]和波浪能发电装置集成于固定的箱式防波堤[3]两种不同的集成方式,进行了基于线性势流理论的频域分析。前一种集成方式采用对称结构,存在极限波能捕获宽度比0.5。后一种集成方式是将浮子作为附属结构装配在固定的透空箱式防波堤前,有很好的适用性和可扩展性。同时,理论分析显示其可以很好地利用反射波能量,波能捕获宽度比可达0.8甚至更高,因此后者具有更为优异的表现。然而上述理论研究是基于线性势流理论进行,波浪非线性、流体粘性和流动分离的影响均未考虑,且仅能够考虑简化为线性阻尼模型的PTO 系统。在实际海况下,波浪的非线性、流体的黏性和流体分离对于共振浮子的运动响应往往具有很强的影响,且波浪能发电装置的PTO 系统的阻尼模型也不仅局限于线性的形式[5],其中液压型PTO 也是常用形式之一,液压型PTO 采用高压和低压蓄压器,可以光滑能量输出,其PTO 阻尼力形式上在半周期近似滑动摩擦阻尼力[6],因此可以用Coulomb阻尼模型近似液压型PTO 阻尼模型。针对以上不足,本文应用基于黏性流的计算流体力学软件OpenFOAM对该模型进行模拟研究,研究线性PTO 阻尼模型Fpto=Cpto·V约束下装置的能量转换性能和消波性能。并与理论分析结果进行对比,分析在共振区间上黏性耗散带来的影响。同时也应用2 种二次平方型,和Coulomb阻尼型非线性的PTO 阻尼模型,研究对比非线性PTO 装置与线性PTO 的区别和联系。同时为改进此类集成装置的能量捕获效率,针对浮子形状进行优化。从而得以获得更高的能量捕获效率。

1 理论基础

1.1 控制方程

本文模型采用OpenFOAM 中的overInter Dy MFoam 求解器求解,流体计算采用有限体积法求解不可压缩的两相流N-S方程,不可压缩连续性方程及动量方程分别为

式中,u为流体的速度;ug为动网格更新时的网格修正速度;ρ为两相流的混合密度;p为压力;S为黏性应力张量;fb为有重力作用的体积力和表面张力项;sρu为源项,可用于阻尼区消波,其中s为阻尼系数。

采用VOF 方法处理两相流界面,VOF 方法的原理是定义体积分数α[0,1],其中0 代表空气相,1 代表水相,两者之间的界面采用0 到1 的过渡值来表示,从而实现界面的捕捉。造波方法采用速度入口造波,通过给定速度和体积分数的入口边界条件而实现数值造波。消波方法采用阻尼区消波的方式,通过在动量方程中添加阻尼项,在消波区内设置阻尼系数大于零,从而实现数值消波。

1.2 重叠网格

重叠网格的基本原理是将不同的部件分别画在不同的网格上,然后融合到一个背景网格上,其中各部件的网格与背景之间网格有重叠区域,利用这些重叠区域网格,通过插值进行信息的双向传递,从而在重叠网格的基础上实现计算域的更新。重叠网格主要包括计算单元(calculated),插值单元(interpolated),洞单元(hole)三类网格(图1)：洞单元网格作为图上黑色网格,为结构内部网格,在计算时间步内的物理量值冻结,不随计算更新;插值单元网格作为图上中灰色网格,为信息传递的主要部分,在子部件和背景网格上分别有一圈插值单元用于双向信息的传递和插值;计算单元为正常参与流场控制方程计算部分的网格,图上灰色网格。可参考沈志荣[7]具体网格插值方法和实现。

1.3 PTO 系统

PTO 阻尼系统采用线性阻尼模型和非线性Coulomb阻尼模型。线性阻尼系统可表示为

式中,λpto为线性阻尼系数,其中最优阻尼系数(λoptimal)可根据势流理论频域下的解析解获得。λoptimal的表达式为

式中,M为质量,μ为附加质量力系数,λ为辐射阻尼,K为水静力回复刚度。

非线性Coulomb阻尼模型可表示为

式中,Coulomb阻尼模型因为其阶跃特性容易引起数值振荡,因此可以做近似的线性化处理如下：

式中,Cpto为预设Coulomb阻尼型PTO 阻尼力,Gpto为线性化位置PTO 阻尼系数。

PTO 阻尼系统采用线性阻尼模型,非线性Coulomb阻尼模型和线性化处理的Coulomb阻尼模型三种阻尼模型如图2 所示。

图1 重叠网格Fig.1 A diagram of the overlapping grid

图2 线性PTO 阻尼模型,Coulomb阻尼模型和线性化的Coulomb阻尼模型Fig.2 Damping models of linear PTO,Coulomb and linearized Coulomb

2 数值水槽构建和模型验证

2.1 模型构建

参考赵玄烈等[3]给出的结构参数构建模型,模型基本布置如图3,水深h=10 m,浮子宽度a1=2 m,后方固定式防波堤宽度a2=6 m,浮子与防波堤间距离D=1 m,浮子吃水深度d1=1 m,防波堤吃水深度d2=2.5 m。此模型的模拟工作难点在于动网格的处理方法,因附属浮子与固定箱式防波堤的距离较近,且共振时浮子运动响应较大。Open FOAM 中传统的随体网格变形不适用于此类在靠近固定边界处的局部网格变形过大的模拟工作。Open FOAM-v1906版本中的重叠网格的功能,可适用于海洋工程浮式结构物的模拟工作,因此本文应用此种网格更新方式。同时可以利用Open FOAM-v1906中的速度入口造波边界进行数值波浪水槽的构建。入口U 边界条件为wave Velocity,相体积分数边界条件为wave Alpha,压力边界条件为fixed Flux Pressure。重叠网格区域边界类型为overset。浮子边界为固壁边界条件。自由液面和重叠网格区域进行如图4的加密处理以满足计算精度要求,网格总数为136 050,近壁面网格大小为0.1 m。时间步长控制采用自动调整时间步长,最大库朗数为0.5。

图3 附属结构式集成装置Fig.3 Layout of the integrated device with a subordinate structure

图4 附属结构形式装置附近重叠网格划分情况Fig.4 Division of the overlapping grid around the integrated device with a subordinate structure

2.2 模型验证

本节验证模型选取一在波浪作用下垂荡方向无约束运动的浮式方箱进行模拟,背景网格和重叠网格如图5所示,近壁面网格大小0.02 m,模型几何参数详以及数值造波的精度验证详见已发表工作[8]。本节应用重叠网格方法进行了浮子在周期T=1.79 s,入射波高H=0.2 m 下的运动响应模拟,并与Isaacson的实验的RAO 值[9]和应用随体变形网格方法模拟的结果[8]进行对比。垂荡方向运动响应历时线如图6,表明应用重叠网格方法进行浮式结构物计算可以获得稳定且可靠的计算结果,进而验证重叠网格方法的有效性。

图5 方箱周围重叠网格网格划分Fig.5 Division of the overlapping grid around the permeable box

图6 重叠网格法模拟的桩式约束方箱垂荡方向运动响应时程与随体变形网格以及实验值的对比Fig.6 The response time history of heave motion of the floating pile-restraint box simulated by overlapping grid method comparing with those obtained by body deformation grid method and by experiments

3 PTO 阻尼模型与浮子形状优化

3.1 线性PTO 阻尼模型

赵玄烈等[3]文中线性PTO 阻尼力选取为单个浮子在线性频域解下的理论最优PTO 阻尼系数,而在考虑黏性的CFD 模拟中,该最优阻尼系数可能不为最优值,且集成系统结构的非对称性也使得附加质量和辐射阻尼发生变化,也导致了集成系统的最优阻尼系数不再与单一浮子相同。因此本节采用线性PTO 模型,从频域下的理论最优阻尼系数出发,研究黏性流下此结构的最优PTO 阻尼的特性。结合理论分析结果,选取模拟工况：T=4.74,4.45,3.88,3.66,3.45,3.30,3.18,3.04,2.84,2.57,2.49和2.39s,对应的无量纲波数(kh)的范围为7.073～1.882,水深和波高设为恒定值(h=10 m,H i=0.5 m)进行模拟研究。

图7为各波况下附加浮子在理论最优PTO 阻尼λoptimal作用下的能量捕获宽度比(Capture Width Ratio,CWR)与理论分析结果的对比。研究发现相对比于单浮子结构形式[8]约0.30的最大CWR值,能量捕获宽度比明显提升,其最大CWR值可达0.7。但是相比于理论分析结果,在共振区间kh=2.0～5.0上,CWR值明显下降,理论最大值接近1.0,模拟值相较于理论值下降约30%,可以明显看到黏性效应对于此类装置能量捕获效率的影响。对于kh=6.089 97和kh=7.07两个短波波况,CWR的极小值和第2个峰值也能够被有效地模拟获得。选取kh=3.72波况,对PTO 阻尼系数进行了放缩,选取放缩系数0.75,1.25,1.5。模拟发现,1.25λoptimal和1.5λoptimal的CWR值都比1.0λoptimal要略大,关于在考虑黏性影响下理论最有阻尼值的讨论详见文献[8]。图8,图9是反射系数(K r)和透射系数(K t)与解析结果的对比。反射系数在共振位置附近出现了下降,在共振位置kh=3.72反射系数达到极小值,意味着反射波波能被吸收。kh=6.09波况反射系数偏小,因为在模拟中此波况下波浪仍然可以引起浮子的振荡。由图7可见,kh=6时CWR不完全是0,可能是由于非线性原因,导致波浪并不是完全的满足了此处的kh值,从而能量也没有被完全反射。

图7 1.0倍最优PTO 阻尼约束下CWR 值与解析解的对比值的对比Fig.7 Comparison between the CWR values and the analytical solutions under the constraint of 1.0 times optimal PTO damping

图8 1.0倍最优PTO 阻尼约束下反射系数与解析解的对比Fig.8 Comparison between the reflection coefficient(K r),and the analytical solution under the constraint of 1.0 times optimal PTO damping

图9 1.0倍最优PTO 阻尼约束下透射系数与解析解的对比Fig.9 The comparison between the transmission coefficient Kt and the analytical solution under the constraint of 1.0 times optimal PTO damping

3.2 非线性PTO 阻尼模型

上节所述线性PTO 模型在微幅低速运动中可以获得较好的近似效果,但当非线性较强,运动响应较大时更适合采用非线性PTO 模型,可选用二次非线性阻尼模型。液压型PTO 装置因为有光滑能量输出的效果,常用于WEC 装置的PTO 系统中,其中Coulomb阻尼模型可作为液压型PTO 的有效近似模型。因此本节选用二次非线性阻尼模型和Coulomb阻尼模型作为集成系统的PTO 装置进行模拟,其中在原型比尺的计算中采用理想的Coulomb阻尼模型未发现明显的数值振荡,可以获得稳定的计算结果,原因可能为原型比尺中模型的流体阻尼和静水回复力可以抵消数值振荡。阻尼系数取λquadratic=λlinear,λcoulomb=λlinearVmax,其中λlinear对应线性PTO 系统在kh=3.01时的理论最优阻尼λlinear=5 720.91 kg/s。Vmax=0.48 m/s为线性PTO 作用下浮子的最大运动速度。如图10为附加浮子在3种PTO 模型作用下,在共振波况T=3.663 s,H=0.5 m 下的运动响应的对比。图11为3种不同PTO 模型的PTO 阻尼力的对比,可以发现,因阻尼系数选取相同,模拟速度低于1.0 m/s,所以二次非线性阻尼型PTO 系统的运动响应比线性PTO 装置运动响应偏大。PTO 阻尼力偏小,并且在PTO 力为0 kg/s的附近表现出二次抛物线形的PTO 力的时程,证明二次非线性阻尼模型可以很好地应用于PTO 系统的模拟。Coulomb阻尼模型因其在半周期上保持恒定最大PTO 力,因此其约束的浮子运动响应最小。线性阻尼模型,Coulomb阻尼模型以及二次非线性PTO 阻尼模型下集成装置的能量捕获宽度比CWR结果如表1所示。可以看到在此种条件下,线性PTO 阻尼模型获得了最大的CWR值。这里其他两种非线性PTO 阻尼模型表现较差。但是也有待于进一步的优化PTO 阻尼系数的选取,以获得更大的CWR值。

图10 3种不同形式PTO 阻尼约束下的浮子垂荡运动响应Fig.10 The heave motion response of the floater under the restraints of three kinds of PTO damping

图11 3种不同形式PTO 阻尼力的时程Fig.11 Time history of the three kinds of PTO damping forces

表1 3种阻尼模型下装置的CWR 值Table 1 The CWR values of the device under three kinds of PTO pumping model

3.3 浮子形状优化

为进一步优化装置的能量捕获效率和消波性能,浮子形状是影响装置能量捕获宽度比的重要参数之一[10],因此本节主要就附属结构中,前方浮子的形状进行优化。由毛艳军等[8]研究可知,方箱型浮子在底部迎浪测和背浪测两个直角处产生了明显的漩涡,从而导致流场粘性效应的增加,因此本节选用2种避免这种结构形式突变的浮子形状,修圆角形式和圆底形式。模拟后,由图12可以看到三者的速度矢量图,方箱形浮子在底部两个拐角处产生了明显的漩涡,漩涡从边壁上分离向外发展并逐渐耗散。修圆角形浮子底部也有漩涡产生,但是可以看到漩涡的尺度较小,且并未脱离浮子的壁面。圆底形浮子底部流场则光滑很多,流体沿着底部壁面发展,对整个流场的扰动较小,从而也对应流体粘性和湍流耗散影响较小。

图12 3种形状浮子周围的流场变化情况Fig.12 The flow field variations around the floaters with three kinds of shapes

3种形状浮子的运动时程如图13 所示,可以看到由于结构水线面宽度相同,排水体积较为接近。从运动响应可以看出,修圆角的浮子和方箱形浮子的运动相位基本上一致,运动响应幅值算子(Response Amplitude Operador,RAO)略微增大。圆底形的浮子在运动相位上与方箱形浮子产生了一定的相位偏移,同时RAO也有所增加。如表2所示,为3种浮子形状算例的透射系数(K t),反射系数(K r),运动响应幅值算子(RAO),捕获宽度比(CWR)模拟性结果对比与方箱形浮子对比,修圆角形浮子和圆底形浮子可以保持透射系数基本上不变,反射系数下降,圆底形浮子的反射系数最小,对应的运动响应和能量捕获宽度比都是最大的,其中圆底形浮子的CWR达到0.808,相比于方箱形浮子,提升了近0.1,效率提升明显。

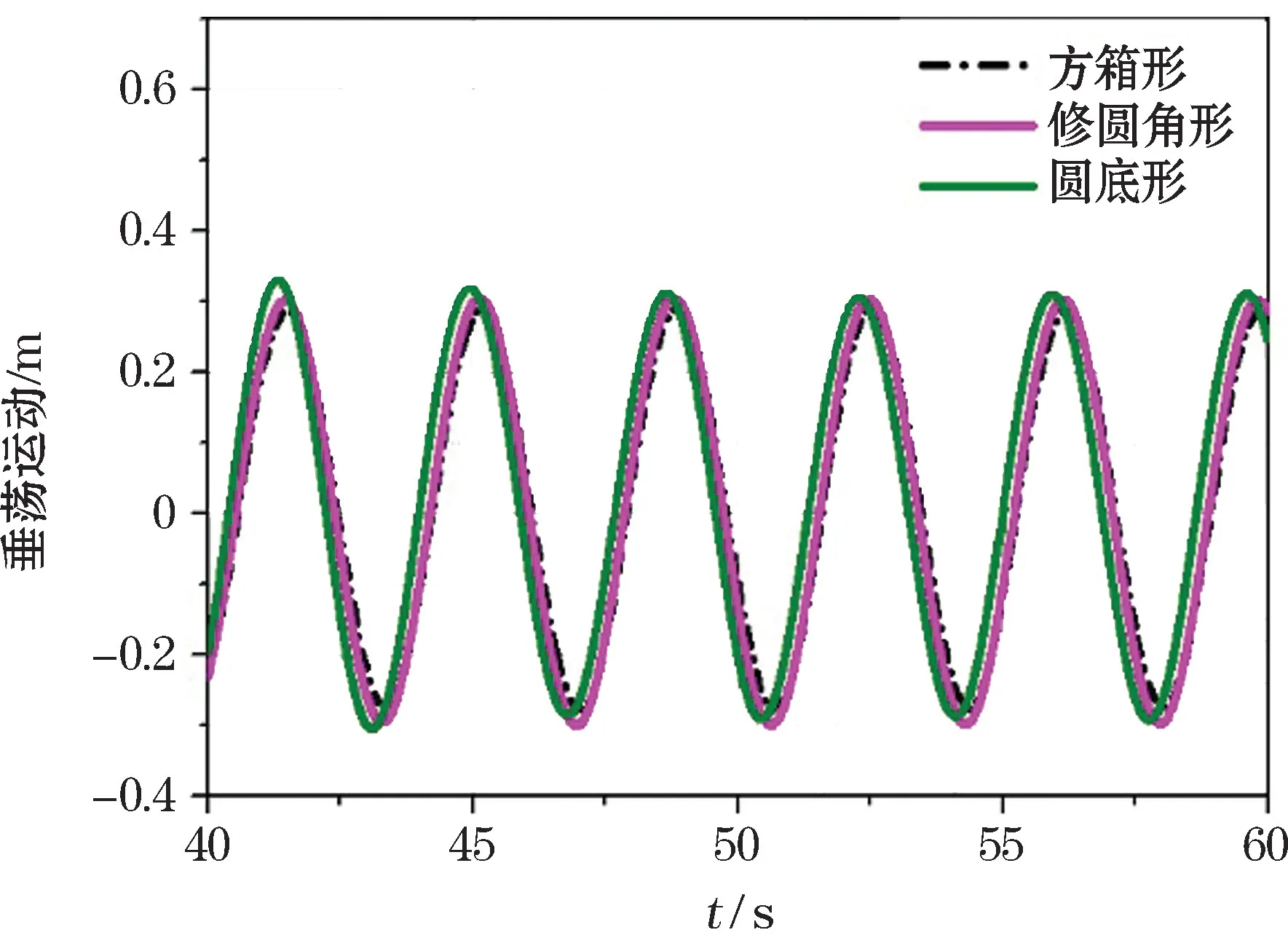
图13 3种形状浮子的垂荡运动响应时程Fig.13 The time history of the heave motion response of the floaters with three kinds of shapes

表2 3种形状浮子的模拟结果对比Table 2 Comparison of the results(K t,K r,RAO and CWR)simulated for the floaters with three kinds of shapes

4 结 论

应用OpenFOAM 进行了附属结构形式的波浪能与防波堤的集成系统的数值模拟工作,分析了考虑黏性和流动分离影响下集成装置的运动响应,能量捕获宽度比和消波性能。通过3种不同形式PTO 系统的对比,研究了PTO 阻尼系统对集成装置的影响。进一步优化浮子形状,研究了浮子形状对装置能量捕获效率的影响。研究发现：

1)此类结构在考虑黏性影响的模拟中仍可以获得较高的能量捕获宽度比,CWR值可达0.7。反射波能量得到很好地利用,反射系数(Kr)在共振区间上降低,同时透射系数(Kt)在kh＞1.8的较宽波频范围内都可以维持在0.5以下,保证良好的消波效果。

2)非线性PTO 的开发和应用,进一步扩展了波浪能发电装置的PTO 模拟工作。2种PTO 阻尼模型可以维持较好的数值稳定性,在本文选取的阻尼系数条件下,非线性PTO 阻尼模型作用的浮子能量捕获宽度比小于线性PTO 阻尼模型。

3)形状参数的优化显示圆底形浮子可以减小流体黏性和流动分离的影响,从而可以进一步提高装置的能量捕获效率。