波浪与抛石潜堤相互作用的MPS法数值模型研究

张永兰蒋 勤*王丽珠

(1.河海大学 港口海岸与近海工程学院,江苏 南京210098;2.南京师范大学 海洋科学与工程学院,江苏 南京210023)

抛石潜堤具有结构简单,易于施工,整体稳定性好等优点,所以它是目前海岸工程中广泛应用的防护结构型式。当波浪行进到抛石潜堤时,部分波浪会在堤前被反射,部分波浪会越过潜堤,还有一部分波浪水体会以渗流的形式透过抛石堤的孔隙传入掩护区内。由于在抛石潜堤孔隙中的渗流水体受到块体摩擦阻力的影响,部分入射波能被耗散,因此抛石防波堤可以起到很好的消波作用。因此,研究波浪与抛石防波堤的相互作用对防波堤设计具有重要的工程价值。

近年来,随着计算机模拟技术的发展,数值模拟方法已成为研究波浪与结构物相互作用的重要手段之一。波浪与抛石潜堤相互作用问题是一个具有复杂流-固界面和大自由表面变形,以及多孔介质渗流的强非线性紊流运动问题。鉴于对抛石体内复杂的紊动渗流问题进行严格的理论求解存在一定的困难,目前通常将抛石结构简化为均质多孔介质,通过建立数值计算模型的方法模拟波浪与可渗结构物的相互作用。对多孔介质内渗流的研究可追溯到19世纪初期,Darcy[1]从流量与压降关系的线性假定出发,提出了分析多孔介质内低雷诺数流体运动的基本原理。Forchheimer[2]针对具有较高雷诺数的渗流问题,在动量方程中引入一个附加非线性阻力项,建立了描述非达西渗流运动的控制方程。Sollitt和Cross[3]通过在动量方程中添加惯性项和线性、非线性阻力项,提出了描述多孔介质中非达西流动的广义渗流模型。Gent[4]基于描述流体运动的雷诺时均N-S方程,并借助“U”型管内一维渗流的实验结果来调整模型中线性、非线性阻力系数的方法,研究了波浪与多孔介质的相互作用问题。Liu等[5]基于流体运动的N-S方程,推导出描述多孔介质内渗流运动的空间平均N-S方程。Hsu等[6]在Liu等[5]的基础上给出了可渗结构内部紊流运动的体平均/雷诺平均N-S方程,以描述介质的孔隙尺寸较大、紊流效应无法忽略的紊流渗流问题。迄今为止,波浪与抛石结构物相互作用的数值模拟大多基于上述多孔介质渗流模型,并采用网格法进行数值求解[6-9]。但是,传统网格法在对动量方程中的对流项和大变形自由表面运动求解时存在着数值耗散问题,难以准确再现具有复杂流-固界面和大变形自由面的强非线性渗流问题。

粒子法作为一种拉格朗日方法,具有易于处理大自由表面变形和不同介质界面以及由于在控制方程中不包含对流项,所以在理论上能够避免数值耗散等优势,可以弥补传统网格法的不足。因此,近年来,采用粒子法模拟多孔介质渗流问题的研究备受关注。Akbari和Namin[10]以及Shao和Loe[11]忽略孔隙介质内外流体运动的紊流效应,分别采用光滑粒子流体动力学法(Smoothed Particle Hydrodynamics,SPH)和不可压缩光滑粒子流体动力学法(Incompressible SPH,ISPH)求解可渗结构物内外的流体运动问题。同样,Fu和Jin[12]忽略渗流的紊流效应,利用移动粒子半隐式法(Moving Particle Semi-implicit method,MPS)建立的数值模型研究了多孔介质河床上的水流流动问题。此外,考虑到波浪与可渗结构相互作用中常伴有波浪破碎等强紊动现象,Ren[13]忽略孔隙介质内部的紊流运动,将大涡模拟技术用于再现孔隙介质外部的紊流运动,建立了分析波浪与可渗结构物相互作用的弱可压光滑粒子流体动力学法(Weakly Compressible SPH,WCSPH)数值计算模型。Peng等[14]考虑孔隙介质内外的紊流运动,基于Drew[15]的二相流混合理论,建立了模拟多孔介质中流体流动的WCSPH 模型。

相较于网格法,无网格粒子法是一种较新的数值流体计算方法,尚存在自由表面粒子误判、压力求解精度较低以及在模拟波浪传播时数值能量衰减显著等问题[16]。因此,本文利用改进的MPS法流体运动模型[16,17]构建了垂向二维紊流渗流数值计算模型,模拟波浪与抛石结构物的相互作用。通过对“U”型管中多孔介质内渗流运动和孤立波在抛石潜堤上传播过程的数值模拟及其与理论解和实测结果的对比分析,对所建立的MPS法紊流渗流模型在用于波浪与可渗结构物相互作用问题时的求解精度进行验证。

1 MPS紊流渗流模型

1.1 控制方程

MPS(Moving Particle Semi-implicit)法即移动粒子半隐式法是由Koshizuka等[18]于1996年提出的一种无网格数值计算方法。它采用带有物理信息的粒子将计算域进行离散,通过追踪离散粒子的拉格朗日运动,模拟流体的运动过程。因此,在采用MPS 法建立模拟多孔介质内外流体运动的数值模型时,基于Drew[15]的二相混合流理论,可以得出描述断面二维多孔介质内外流体运动的控制方程为

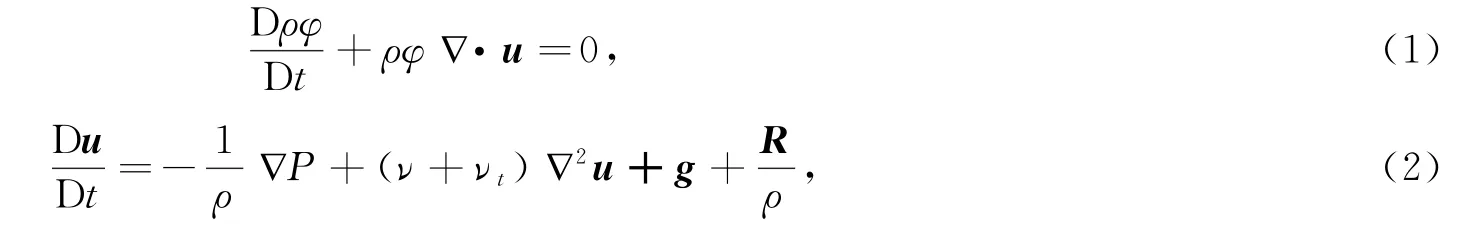
式中,u为速度矢量;ρ为密度;t为时间;P为压强;g为重力加速度;ν为运动黏度;φ为孔隙介质内流体所占体积的百分比,即：φ=VF/V,VF为液相体积,V为多孔介质的体积;R为多孔介质对孔隙水流的阻力;νt为紊流黏性系数,可采用Smagorinsky紊流模型[19]计算,即νt=(CsΔl)2(2SijSij)1/2,其中Cs为Smagorinsky常数,在本模型中取Cs的值为0.1,Δl为粒子初始间距,Sij为应变张量,i=1,2,j=1,2。

在上述基于二相混合流理论[15]的方程中,包含了流体和固体(多孔介质骨架)两相。本文假定多孔介质骨架不随外力变形,因此无需求解固相运动。同时,假定多孔介质内流体处于饱和状态,流体穿过多孔介质区所受到的阻力为R,根据Peng等[14]的计算方法,R的计算公式为

式中,μ为动力黏性系数;kp为渗透性系数;φ为体积分数;Dc为抛石块体的平均粒径,本文取Dc=d50。

当采用MPS法进行数值求解时,首先利用核函数(或称权重函数)建立粒子间相互作用模型。然后,对控制方程进行离散求解,以实现对流体运动过程的数值模拟。MPS法以目标粒子与其相邻粒子间的距离远近来描述粒子间相互影响的程度,最常用的核函数为Koshizuka等[18]于1996年提出的标准核函数w(rij),具体公式为

式中,re为目标粒子的影响域半径;rij为粒子i和粒子j之间的距离,即rij=|rj-ri|,ri和rj分别为i,j粒子的位移矢量;。参考以往的研究经验,对于梯度模型,取re=2.1l0;对拉普拉斯模型,取re=3.1l0,在此l0表示初始粒子分布的粒子间距离,即离散粒子的直径。

通过构建梯度(∇φ)算子、拉普拉斯(∇2φ)算子和散度)的离散模型对控制微分方程进行离散,实现对流体运动过程的数值求解。常用的算子的离散模型为

式中,φ为任意的一个标量为任意的一个矢量;Ds为数值计算模型的空间维度,对二维数值计算模型Ds取值为2;n0为初始粒子数密度;λ为一个模型参数,定义为

粒子数密度n是流体密度在 MPS 法中的一个衍生变量,在物理含义上两者是对等的。MPS法通过在计算过程中保持流体的粒子数密度不变来满足流体的不可压缩条件。粒子数密度n是一个无量纲参数,定义为目标粒子i与其影响域内所有相邻粒子j之间的核函数值的累加值,具体表示为

1.2 压力泊松方程

与SMAC法类似,MPS法采用映射法对离散后的控制方程进行求解。针对某一时步,模型的求解过程分为两步：第一步为预测步,对动量方程中除压力梯度项以外的所有项进行积分,得到一个临时的速度场和位移场;第二部为校正步,考虑流体的不可压缩条件,对包括预测步中未使用的压力梯度项的动量方程进行积分,推导出压力泊松方程,通过求解压力泊松方程得到新的压力场,再采用压力梯度项对预测步得到的临时速度场和位移场进行修正,求出下一时步物理量的计算结果。

具体地,在采用MPS法进行数值求解时,目标粒子i在k+1时步的流速可以拆分为中间流速和校正流速)之和,即

式中,i代表目标粒子。根据由Drew[15]的二相流混合理论得到的动量方程式(2),在预测步中,目标粒子i的中间流速可以采用上一时步k得到的重力、黏性力以及阻力项的值显式求解,即

式中,Δt为计算时间步长。在MPS法中,预测步对应于虚拟时间步k+1/2,用“*”表示。在校正步中,目标粒子i在k+1时步的流速为中间速度矢量和源于压力梯度的修正流速矢量之和,即

对式(11)两边同时求散度,可得

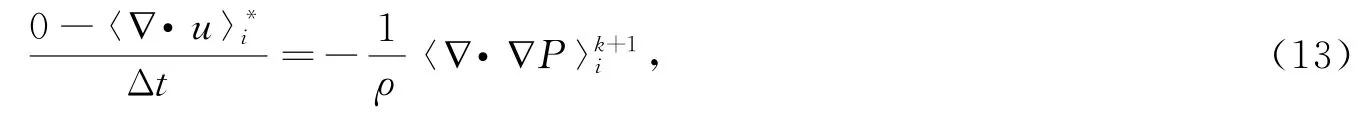
结合式(1)可得

最后,综合式(13)和式(14),可以得到可渗结构物内的压力泊松方程为

式中,ρ为流体密度;n0为初始粒子数密度为k时步的粒子数密度为k时步粒子i的体积分数其中,nw为可渗结构物孔隙率,Ωi为目标粒子i的邻域搜索范围,其直径等于可渗区域过渡区厚度,w(rij)为表征目标粒子i与其相邻粒子j之间相互关系的核函数。

1.3 压力梯度模型

为了避免因原始压力梯度模型计算精度低而引起的数值能量耗散问题,本研究采用Wang等[16]基于泰勒级数展开提出的高精度压力梯度模型,其表达式为

1.4 自由表面粒子的识别

与网格法中需要采用特殊的自由表面追踪方法相比,无网格粒子法的最大优势之一是可以自然、简单地实现自由表面的追踪模拟。在原始MPS 法中,自由表面粒子的识别依据自由表面处粒子的影响域被自由表面边界截断,其粒子数密度小于内部流体粒子的粒子数密度的特点,给出的自由表面粒子的判别条件为：

式中,β为经验系数,一般取值为0.80～0.97,本研究β=0.95。

式(17)中的自由表面粒子的判定条件简单易行,但是,当内部流体粒子的分布不够均匀、混乱无序时,内部的流体粒子常常被误判为自由表面粒子,从而引起严重的非物理压力震荡问题。因此,本研究采用Wang等[19]提出的压力判别法来提高自由表面的识别精度,即：在式(17)的自由表面粒子判别条件的基础上,引入以压力值为参数的附加判别标准：

1.5 流-固界面的耦合

为了保证流体运动的连续性,需要对流体与多孔介质间的流-固界面进行特殊的边界处理。在传统欧拉网格法中,通常依据连续方程和动量守恒方程,在流-固界面网格上施加相应的流速或压力等的连续条件。而在MPS粒子法中,由于离散流体粒子具有拉格朗日特性,粒子的位置坐标是随流体运动不断变化的,因此无法像传统网格法那样在离散粒子上施加相应的边界条件。因此,本研究借鉴Akbari和Namin[10]的边界处理方法,在流体域和多孔介质域之间设置一个孔隙率渐变的过渡区域(图1),使得流体粒子进出多孔介质时受到一个连续变化的阻力作用,以实现多孔介质内外流体运动的连续性。由于实际问题中可渗结构物界面一般具有不规则的几何形状,难以精准再现可渗界面,因此,可渗界面通常被视为具有一定范围的一个流-固过渡区域,这一过渡区域的大小可根据组成可渗结构物的材质的平均直径来确定。前人的研究结果[19]表明：当选取的过渡区域的厚度δ小于可渗结构物材料的平均粒径(δ＜d50)时,将导致数值计算的不稳定;当选取的过渡区域厚度δ大于可渗结构物材料的平均粒径(δ＞d50)时,所选取的过渡区域厚度越小,计算结果的精度却越高。通过模型模拟试算,本文将可渗结构物材料中值粒径值(δ=d50)作为流-固过渡区域的计算厚度。

图1 流-固界面耦合示意图Fig.1 A sketch map showing the coupling at the fluid-solid boundary

2 模型验证与结果分析

2.1 “U”型管内多孔介质渗流

对“U”型管中多孔介质内渗流问题进行了数值实验研究,分析了 由“U”型管两端液面差引起的多孔介质内不同时刻的渗流速度和液面变化过程。数值实验的计算条件为“U”型管长B=4 m,高H=3.8 m,在“U”型管底部中央区设置了宽Lp=1 m,高Hp=1 m的多孔介质结构物;“U”型管左端初始水柱高HL=3.35 m,右端水柱高HR=2 m,左右端水位差ΔH0=1.35 m(图2)。由于“U”型管两端水柱高度不同,在重力作用下,左侧水体会穿过多孔介质渗流到“U”型管的右侧,当管内两端液面高度持平时达到最终的平衡状态。

图2 “U”型管内渗流概化图(m)Fig.2 A sketch map of seepage flow motion within a U-shaped pipe(m)

式中,t为时间;ΔH0为“U”型管左右两侧水柱的初始水位差;LP为渗流路径的长度;kh为导水率,即kh=ρgkp/μ。其中g为重力加速度;kp为渗透性系数;μ为流体的动力黏性系数;ρ为流体密度。

同理,多孔介质内渗流速度随时间变化的理论公式为

采用线性达西渗流的假设[1],忽略式(4)中第二项的非线性阻力项,可得渗流水头ΔH0随时间变化的理论公式为：

式中,t为时间;ΔH0初始水位差;LP为渗流路径的长度;u为多孔介质内的达西渗流速度。

为了与理论值进行比较,采用所建立的MPS法渗流模型,选取离散粒子直径l0=0.05 m,粒子总数N=5 000,流体密度ρ取水的密度1 000 kg/m3,流体的运动黏滞系数ν为10-6m2/s,对“U”型管中多孔介质内渗流进行了数值模拟。对比分析当kh为0.05和0.025时计算得出的“U”型管两端水柱水头差随时间变化的数值解与理论值(图3)可见：在两端水头差较大的初期阶段(t≤10 s),由于两端液面高度差较大,重力作用较强,数值解与理论值均给出了液面差急速下降的变化趋势,二者间的误差低于10%;此后,随着两端液面差逐渐变小,数值解与理论值给出的液面差变化速度变缓,最终达到平衡,计算值与理论值间的误差低于20%。相应地,对比分析管内可渗区中心断面平均渗流速度随时间变化的数值解与理论值(图4)可见：模型模拟结果与实验得到的渗流速度的变化趋势与液面水头差变化趋势基本一致,即在初期阶段(t≤10 s),平均渗流速度随时间急速减弱;此后平均渗流速度缓慢下降。数值计算得到的平均渗流速度与理论值间的误差低于15%。

图3 不同时刻液面差变化计算结果与理论值比较Fig.3 Comparison between the calculated results and the theoretical values of the variations in water level difference at different time

图4 不同时刻平均渗流速度的计算结果与理论值比较Fig.4 Comparison between the calculated results and the theoretical values of the averaged seepage velocity at different time

2.2 抛石潜堤上孤立波传播

采用本研究建立的MPS渗流模型对孤立波在抛石潜堤上的传播过程进行了模拟研究,并与Wu和Hsiao[21]的物理模型实验结果进行了比较。依据物理模型实验,计算域设置如图5所示,水槽长L=8 m,水深d=0.11 m,在水槽的左端采用推板式造波,入射波高为H=0.047 7 m。在水槽中部距水槽左端4 m 处设置了长B=13 cm,高h=6.5 cm 的矩形抛石潜堤。组成抛石潜堤的碎石平均粒径d50=0.015 m,孔隙率nw=0.52。计算中,将抛石堤前趾堤脚作为坐标原点,分别在堤前1.8 m(x=-1.8 m)处和堤后1.8 m(x=+1.8 m)处设置P1和P2两个测波点,记录孤立波的波面形态;离散粒子直径取l0=0.005 m,离散粒子总数N=27 000个;流体密度ρ=1 000 kg/m3,运动黏滞系数ν=10-6m2/s。

图5 孤立波在可渗潜堤上传播概化图Fig.5 A sketch map of solitary wave propagation over submerged permeable breakwater

不同时刻(t分别为1.45,1.85,2.05和2.25 s)潜堤附近压力场与流速场的模拟结果如图6所示。需要说明的是本研究将孤立波波峰到达x=-1.8 m 处的瞬间定义t=0 s。由图6a可见,在流-固界面处粒子分布均匀,且压力分布的连续性较好,表明本研究所采用的流-固界面耦合的边界处理方法是合理可行的。由图6b可见：当孤立波传播到堤前趾附近时,由于受到抛石潜堤的阻碍作用,波浪水质点速度明显减弱。在堤的后方由于波浪水流速度的垂向差异,形成了明显的紊流涡旋,且涡旋的尺度和强度随时间逐渐增大。在t=2.05 s时,涡旋基本发育成熟,到t=2.25 s时,涡旋充分成长,涡旋外围延伸到自由液面附近。由图6a的压力场和图6b的流速场的模拟结果可见：本数值模型有效地保证了压力场的均匀变化,无明显数值压力震荡,合理地再现了潜堤后方紊动涡旋的形成发展过程。

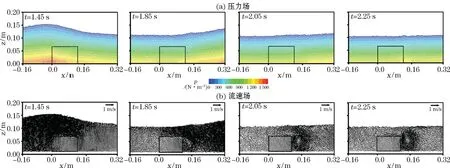
图6 不同时刻(t=1.45 s,t=1.85 s,t=2.05 s,t=2.25 s)潜堤周围压力场和流速场模拟结果Fig.6 Simulated results of the pressure fields and flow speed fields around the submerged permeable breakwater at different time(t=1.45 s,t=1.85 s,t=2.05 s,t=2.25 s)

对比由MPS数值模型得到的抛石潜堤前后孤立波波面历时曲线与Wu和Hsiao[21]的实验结果和Gui等[22]ISPH 模拟结果(图7)可知：在x= -1.8和1.8 m 处,本数值模型得到的孤立波波面形态变化与Wu和Hsiao[21]的实验结果基本一致,同时,相较于Gui等[22]采用ISPH 法得计算结果,本模型的模拟结果与实验值更为接近。

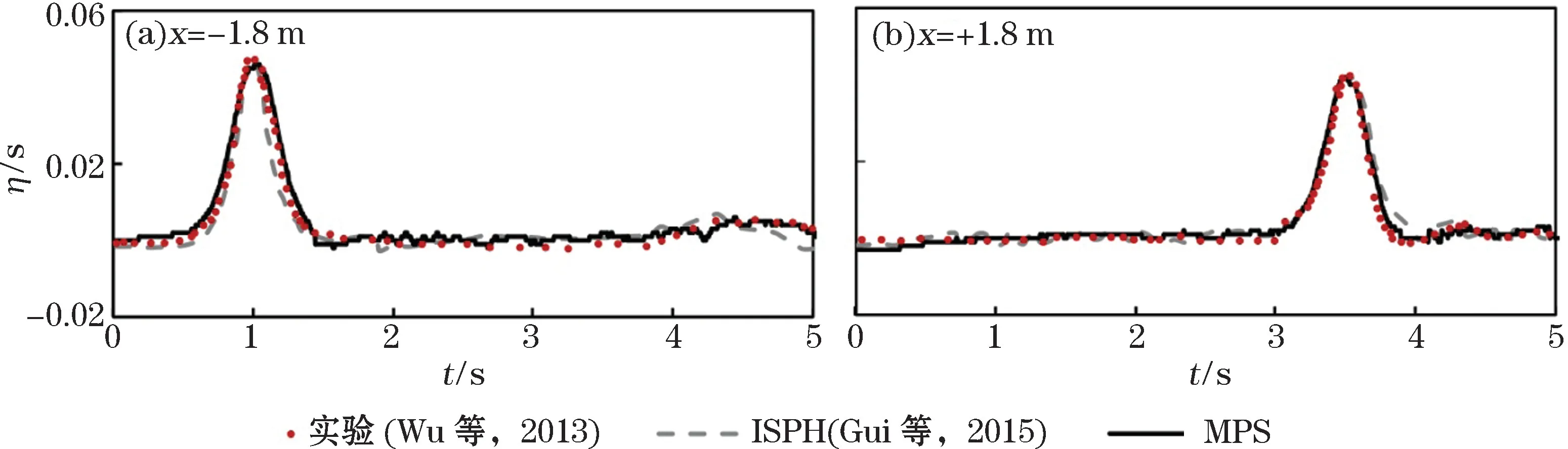
图7 抛石潜堤前后孤立波波面形态模拟结果与实测值比较Fig.7 Comparison of the calculated and the measured profiles of solitary wave in front and back of the submerged rubble-mound breakwater

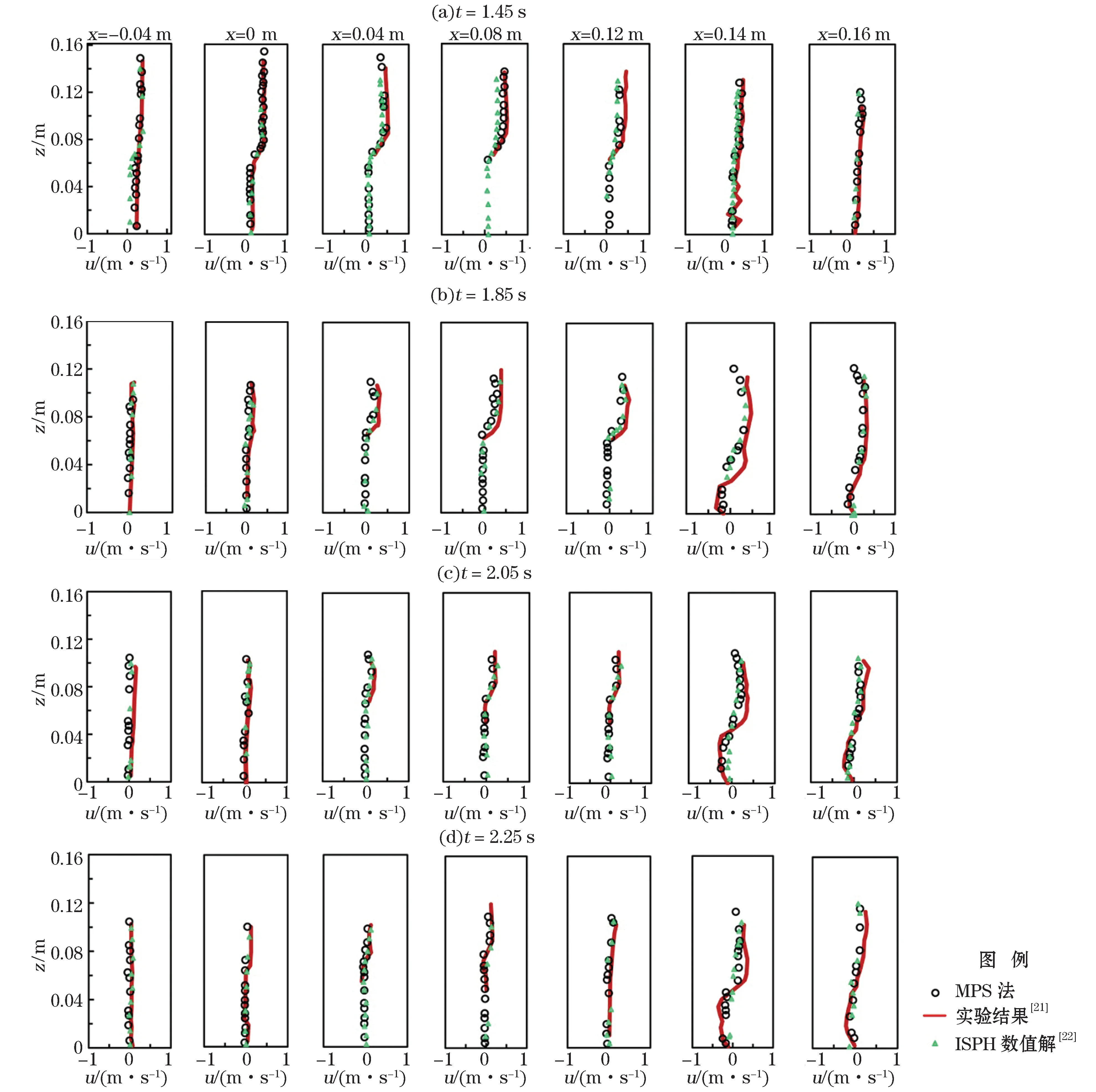
图8 潜堤周围典型断面水平速度垂向分布对比图Fig.8 Comparison of vertical distributions of horizontal velocity along typical sections around permeable structures

图8为不同时刻(t=1.45,1.85,2.05和2.25 s)典型断面(如表1所示)的水平流速垂线分布的MPS法模型模拟结果与Wu和Hsiao[21]的模型实验结果和Gui等[21]的ISPH 法模拟结果的比较。相较于Gui等[22]采用ISPH 法得到的模拟结果,本模型给出的各断面的流速分布总体上与实验结果更加接近。此外,从图8b～8d可见,在断面x=0.16 m 处,断面流速分布的数值计算值与实验值间的误差明显大于其他6个断面。结合图6b可以发现,在x=0.16 m 处的流速变化比较复杂,并伴有涡的产生和消失,由于目前的数值模型是将抛石结构物假设为均匀的多孔介质结构,不能再现实际抛石结构物中复杂的孔隙结构,因此导致在流速变化复杂的区域模型得到的流速值与实验值尚存在一定的差异。

表1 流速测量点x 方向坐标表Table 1 The x coordinates of the flow velocity measuring points

2.3 模型收敛性验证

为了验证所建立的数值计算模型的收敛性,采用不同的离散粒子解像度对计算结果的模拟精度进行了分析。图9为粒子直径分别为l0=0.005 m,l0=0.006 m 和l0=0.008 m 的条件下得到的t=2.25 s时刻,不同断面(x= -0.04 m,x= +0.04 m,x= +0.12 m)上水平流速垂向分布计算结果的对比图。由图9可见,3种不同离散粒子尺度下的计算结果差异很小,并与实验值基本吻合,表明所建立的MPS渗流模型是收敛的。

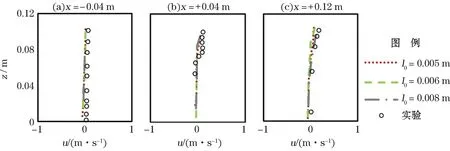
图9 不同粒子解像度条件下水平流速计算结果比较Fig.9 Calculated horizontal flow velocities under the conditions of different resolutions

3 结 论

本文以Wang等[16,19]提出的改进MPS法流体运动模型为基础,基于Drew[15]的多孔介质二相流运动方程,采用Gotoh等[23]提出的亚粒子尺度(SPS)紊流模型,构建了垂向二维MPS法紊流渗流模型,用以研究波浪与抛石潜堤相互作用。通过模拟“U”型管中多孔介质内渗流运动和孤立波在抛石潜堤上的传播过程,验证了本模型的合理性和模拟精度,具体结论为：

1)对“U”型管中多孔介质内渗流问题的模拟研究表明：模型得到的不同时刻“U”型管两侧水柱液面差和管内渗流区中心断面水平速度平均值变化与理论值基本吻合,变化趋势一致,证明本文提出的MPS法紊流渗流模型可已很好地模拟线性渗流问题。

2)由孤立波在抛石潜堤上传播过程的模拟结果可见：由本文建立的数值模型得到的孤立波波面形态、渗流区内外典型断面上垂向流速分布的计算结果与实测结果吻合较好;计算得到的压力场分布均匀、无明显的数值压力震荡;流速场的计算结果清晰地再现出波浪与抛石潜堤相互作用过程中的涡流现象及其运动过程,表明本模型在模拟具有复杂介质界面和大自由表面变形的非线性渗流问题时具有显著优势。

3)通过对不同解像度条件下渗流区典型断面水平流速垂向分布的模拟结果与实测值的比较,验证了本数值模型具有良好的收敛性。