高中数学教学中审题能力的培养途径
江苏省前黄高级中学国际分校 潘 莉
审题是高中数学教学中的一个重要环节,学生只有正确而有效地审题,才能读懂题意,迅速找到题目中的关键信息,并进行有效整合,形成清晰的思维活动,从而制定一个最佳的解题方案或策略,高效地解决学习中遇到的问题。学生审题能力的高低,直接影响学生的解题速度与运算的准确性。
一、培养学生严谨审题的能力,正确理解题意是关键
审题的关键是准确理解题意。在审题的过程中,要对题目中出现的条件、定义、概念等进行充分的阅读与理解,还要注意题目中的关键语句,分析出关键信息。在数学教学中,教师要引导学生认真读题,引导学生正确理解题目中的意思,对题目中的信息进行有效加工,对有关条件进行合理转化,形成正确的解题方案。
例1:若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点。设函数y=f(x)=x3-tx2+1(t∈R)。
(1)若函数f(x)在区间(0,1)上无极值点,求t的取值范围;
(2)求证:对任意实数,在函数f(x)的图像上总存在两条切线相互平行;
分析:审题时首先要认真读懂题目,抓住函数极值点的定义,正确进行分析。第一问可以直接求出导数为零的方程的解,从而将根与范围(0,1)进行比较,可得结果。第二问要理解“任意”“总存在”等一些关键词,利用导数与斜率的关系写出直线方程,进一步分析可得结果。

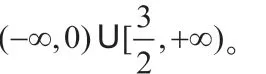
()2 由(1) 知f'(x)=3x3-2tx, 令f'(x)=1, 则3x3-2tx-1=0,
所以不论为何值,函数f(x)的图像在点x=x1,x=x2处的切线平行。
综上,对任意实数t,函数f(x)的图像总存在两条切线相互平行。
二、培养学生深入细致审题的能力,充分挖掘隐含条件是关键
学生在解题的过程中有时会过分地追求速度,对审题往往缺少耐心和细心,造成审题失误,关键信息未能捕捉到,或者隐含条件未能深入挖掘,导致解题不能进行或计算出错。教学中,教师要引导学生认真读题,并对题目中的关键信息及时进行圈点勾画,提高审题效率。
例2:若sinθ,cosθ是方程4x2+2mx+m=0 的两根,则m的值为___________________。
分析:题目中的显性条件是sinθ,cosθ是方程4x2+2mx+m=0的两根,可以选择韦达定理或把方程根代入方程中去,隐性条件是三角函数相关公式,通过计算可以得到m的值,但还要注意通过判别式进行检验。
三、培养学生全局处理问题能力,全面分析,整合信息是关键
数学审题要有全局观念,认真阅读题目,分析题目中的每一个条件并进行适时转化,将问题进行分解,从而化难为易、化繁为简,高效审题,提高解题效率。

(1)求函数q(x)的表达式;
(2)当x为多少时,总利润(单位:元)取得最大值,并求出该最大值。
分析:学生在审题的过程中要注意到一些关键性的信息,如“销售量q(x)(单位:百台),若x<20,当20 ≤x≤180 时,若x>180”,这些都是处理问题的关键。
四、培养学生灵活审题的能力,创新、发散思维是关键
波利亚在《怎样解题》中指出:“通过对解题活动,特别是已有的成功深入分析总结出一般性的思维方法或模式,而后者在今后的解题教学活动中就可起到一定的启发和指导作用。”“它会给你指出整个或者部分解题途径,它或多或少地清楚地向你建议该怎么做。”
多层次、多角度地分析问题,更加有利于我们多角度地去思考问题,从而解决问题的方法、策略就越多。教师在教学过程中要培养学生多维度分析问题的能力,加强一题多解和多题一解的训练,这样学生才能在考试过程中在较短的时间内利用最有效的方法解决问题。
分析:本题可以从函数图像的角度分析,将其看成一个分段函数来处理,分别研究一次和二次函数的情况。同时也可以先分离参数,再转化成图像去处理。

总之,要让学生能够熟练掌握解题的方法,首先要掌握审题的方法和技巧。只有学生正确审题,才能在较短的时间内迅速找到解决问题的方法,从而进一步正确解决问题。在数学教学中,要注重学生审题能力的培养,只有认真、细致地审题,才能全面客观地掌握解题信息,并进行合理转化,从而形成良好的解题思路。

