小学数学教学中如何培养学生的关联思维能力

淮阴师范学院第一附属小学 朱凯敏

小学数学教学改革深入推进，培养学生关联性思维能力成为提高学生学习主体地位与教学质量的重要前提。但关联性思维能力培养是系统性工程，还需从学生已有的认知经验入手，找准其单点思维起点，并通过双向交流互动等途径，丰富学生多点思维。这要求教师转变职责理念，提高学生学习的主观能动性，引导其多角度观察事物，从而培养关联思维，灵活解决生活问题。

一、依托教材明确学生思维发展起点

数学知识逻辑性强，需要学生多角度分析与验证数学知识，从而深入了解概念内涵。但学生在接触新的数学知识时，多从已有的学习经验或生活认知入手分析数学知识，数学问题解决方法相对单一。而学生的知识基础与思想模式不同，解决数学问题的角度也存在差异，实现学生单点思维向多点思维的发展，还需找准学生单点思维的起点，带领学生巩固以往的数学知识，通过新旧知识结合，引导学生多角度发现问题解决方法。如在《小数的乘法与除法》的教学中，在探索新知环节，让学生运用以往学过的方法，看计算结果是否与猜想一致，实现思维自然过渡，轻松掌握小数乘整数的计算方法。

二、小组合作丰富多点思维

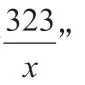
三、通过思维成果展示形成多点思维

小组合作学习得出的规律性总结，得益于组内成员的有效沟通与交流，但并不保证所有的学生都没有疑问。在班内展示小组多点思维成果，其他小组成员质疑与点评、辨析，更利于多点思维成果的丰富性。通过互动展学，学生倾听与提出问题、表达等良好习惯得以养成，更重要的是对各思维要点的掌握更加明确。在多个单点思维的比较中，思维途径得以拓展，多点思维得以丰富与完善。如在求证直角三角形的问题中，各个小组虽然得出了作辅助线、用相似、证相等、用勾股定理等思维方式，但在全班互动展学中，积极吸取了其他小组验证得出的导角、余角补角等解决方法，在实现多点思维拓展的同时，也加深了对直角三角形知识的理解。

四、教师灵活演变角色

在小学数学教学中，要想快速培养学生的关联思维能力，应当注重学生主体地位的提升。对此，要求教师灵活转变组织者与引导者等角色，让学生在双向互动交流中不断发展多点思维。学生在小组合作学习中，认识与学习到了多样性的思维方式，但对各思维方式的关联与核心等问题相对忽视。教师需要给予适当的引领，通过设计问题等方式，引发学生思辨讨论，让学生通过对比等方法，明确思维方式的核心与起点等。尤其是在解决数学问题时，鼓励学生多角度思考解决方法，引导学生整体性地看待问题，最终养成关联性思维。最常用的是一题多变教学方法，围绕同一道题，从解法或分析、检验等方面进行变换性的提问，能够灵活学生思维，使其发现多个思维方式之间的关联度。变问题或条件等思维训练，要求学生对法则或公式明确掌握，确保思维定势积极作用的有效发挥，夯实学生知识基础。

提高思维能力是培养学生综合能力的核心，也是激发学生智力与潜力的重要前提。小学阶段的学生生活阅历与学习体验不足，思维水平相对滞后，常处于定势思维状态，与其他思维的关联度相对不足。单点思维不利于学生核心素养的发展，还需依托教材与生活素材活化学生思维，培养其举一反三与融会贯通的学习能力，促使其逐步走向多点思维发展状态，最终形成关联性思维。