结合尺度估计MST和粒子滤波的视频目标跟踪

孙新领，张 皓，赵 丽

1.河南工学院 计算机科学与技术系，河南 新乡453003

2.山西大学 软件学院，太原030013

1 引言

视觉跟踪是计算机视觉中最重要的领域之一，已被应用于多个领域，例如监控和人机交互等。但是，当存在遮挡、外观和尺度变化情况下，仍然会引起各种问题[1-3]。在各种视觉跟踪算法中，均值漂移跟踪（Mean Shift Tracking，MST）算法[4-6]是最常用的方法之一，它具有易于实现且计算时间消耗较少的优点。MST方法的基础是非参数密度估计器，由于它是使用颜色直方图来表示模型，所以对部分遮挡和旋转具有鲁棒性。然而，MST 方法不能解决尺度变化、完全遮挡和模型改变等问题。此外，在外观和光照变化的条件下实现长期跟踪也十分困难[7-8]。

为了解决MST 的这些缺点，研究者已经提出了多种基于MST 的改进型跟踪方案。例如，文献[9]给出了一种改进的MST算法（EM-Shift），其同时估计局部模式的位置和描述局部模式近似形状的协方差矩阵。文献[10]利用自适应背景加权直方图（BWH）方法来改进MST算法，并尝试将轮廓直方图和空间直方图结合起来，使其可以利用背景信息，有效地减少背景对目标定位的干扰。但是，它无法处理对象的尺度变化。文献[11]提出了一种称为尺度和方向自适应MST 算法（SOAMST），使用加权图像作为密度分布函数的尺度和方向，使其可以在MST 框架下估计物体的尺度和方向。但是SOAMST 算法对于目标的遮挡问题也无法处理。为此，一些学者融入了卡尔曼滤波器。例如，文献[12]提出了一种将卡尔曼滤波与SOAMST 相结合的算法（KSOAMST），如果目标被部分遮挡，则直接使用SOAMST跟踪目标；如果完全遮挡，则使用卡尔曼滤波器估计目标下一帧的位置。但是，卡尔曼滤波的性能随着非线性强度变大会明显下降。文献[13]使用MST进行跟踪，并利用它的相似性来调整卡尔曼滤波器的协方差。这种方法可以在被遮挡的情况下追踪物体，但当物体移动速度变化较大时，无法跟踪物体。

在本文中，提出了一种结合MST算法、探测器和粒子滤波器的目标跟踪方法。主要创新点为：提出一种具有半监督学习能力的探测器来在线更新目标模型，自适应校正目标尺度，以此解决传统MST 方法无法应对尺度变化的缺陷。此外，在发生完全遮挡时采用粒子滤波器估计目标的位置，以此改善MST 无法处理完全遮挡的问题。实验结果表明，该方法能够成功跟踪复杂环境中的目标。

2 目标跟踪方法的框架

本文所提出的目标跟踪方法的流程图如图1所示，主要包括MST、探测器和粒子滤波器。首先，通过MST算法跟踪对象，基于Bhattacharyya系数来确定是否跟踪成功。如果该系数值低于特定阈值，则判定未成功跟踪对象。此时，使用探测器重新初始化MST 的目标位置和尺度。这个过程是基于模型匹配和学习过程。学习过程会不断更新目标模型，以加强探测器的性能。另外，粒子滤波器还可以准确地估计目标的位置，在发生完全遮挡时，通过目标的先前行为来预测目标的位置，以此解决经典MST算法的缺点。

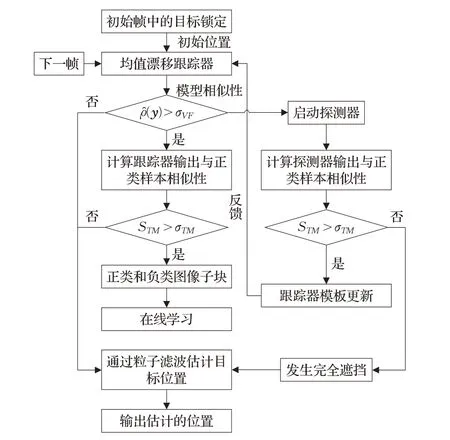
图1 所提出跟踪算法的流程图

在发生完全遮挡的情况时，MST 和探测器都无法找到目标。如果跟踪器和探测器的相似性快速降低，则确定已发生完全遮挡，并且启动粒子滤波器预测目标的位置。在所提出的方法中，假设目标在x 和y 方向上以相同的速度移动。这种假设是合理的，因为完全遮挡通常会在短时间内发生，因此目标遵循几乎恒定的速度模型。粒子滤波器可以根据目标的先前行为估计目标的位置和速度。在离开遮挡情况之后，再次由探测器找到目标并继续跟踪。

3 均值漂移跟踪器

3.1 均值漂移算法

在经典的MST算法中，用户在第一帧中选择目标，并且使用归一化的颜色直方图来表示目标模型[14]。目标区域中的归一化像素位置由确定，其中n 表示像素的数量。目标模型由下式计算得到：

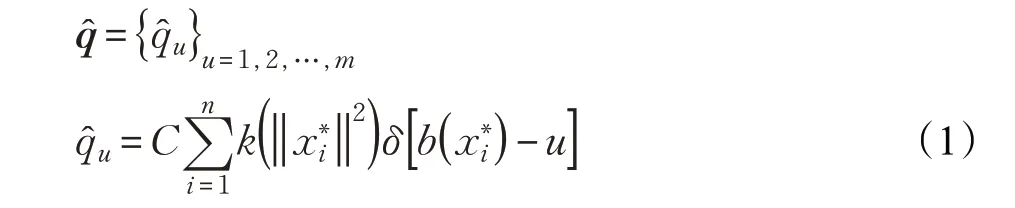
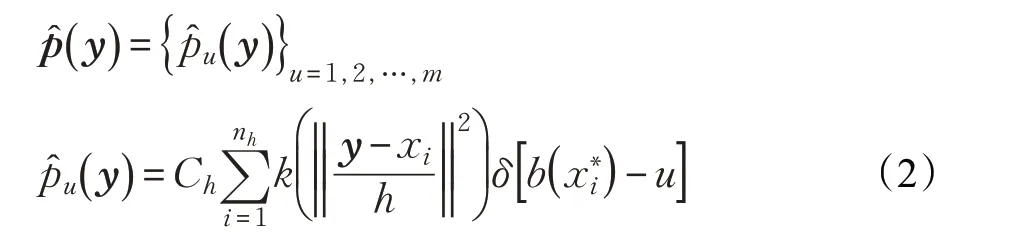
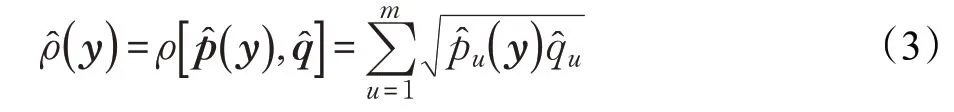
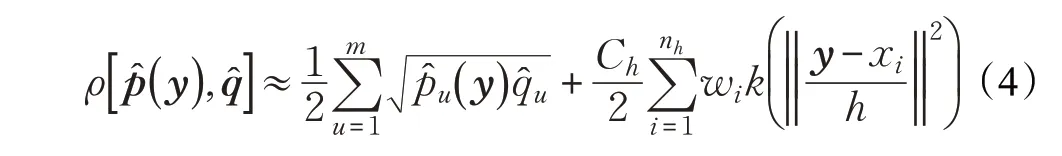
其中：

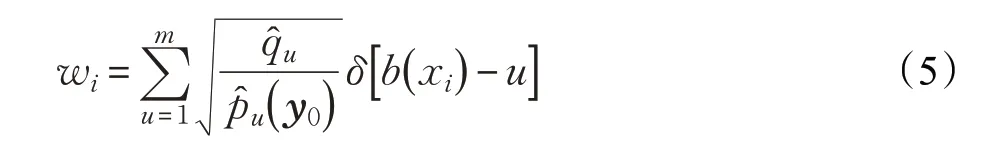
式（5）中的第一项与位置y 无关，所以最大化相似性与最大化式（5）中的第二项相同。将式（5）对y 求导数，并使其等于零，得到迭代优化过程，称为均值漂移迭代。在均值漂移迭代中，估计的目标从y0移动到新位置y1。经典MST的最终迭代公式定义为：

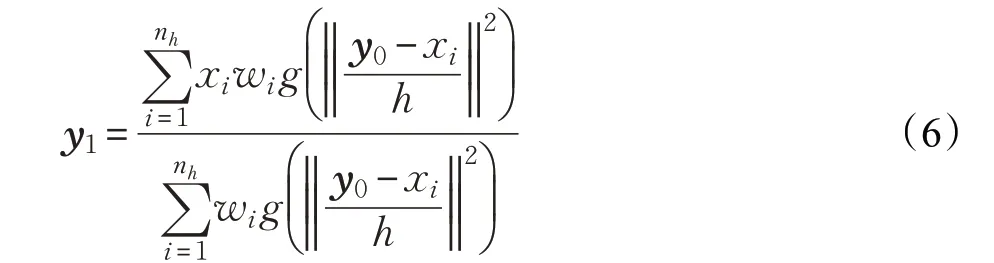
MST 算法适用于跟踪通用对象。但是，当连续帧之间的目标位移相对较大时，它可能无法跟踪对象。类似地，如果目标与其他对象重叠（遮挡），则算法可能会收敛到局部最小值。为解决这个缺点，需要重新初始化或重新启动检测过程。此外，经典MST 的一个局限是尺度适应性。因为它不考虑目标的尺度，所以无法准确估计目标的位置。

3.2 跟踪器的模型更新

为了解决MST 的尺度问题，需要动态更新MST 跟踪器的目标模型，为此本文采用一种探测器来实现模型的更新。如果跟踪器无法跟踪目标，此时探测器能够以高可靠性找到目标，并更新目标模型。其以加权方式更新目标的颜色直方图，表示如下：

4 具备在线学习的探测器

探测器有助于重新初始化MST 的目标尺度和位置。当采用半监督P-N 学习[17]的在线学习过程跟踪物体时，探测器的性能得到有效改善。探测器基于滑动窗口方法[18]，由三个部分级联组成：方差滤波器部分、集成分类部分和模型匹配部分。为了实时执行提出的算法，探测器在验证区域中搜索目标，而不是执行穷举搜索。

4.1 方差滤波器

探测器执行的第一步是使用方差滤波器在图像中找到候选子窗口。通常，方差可以区分开结构良好的对象和均匀背景。在该阶段，将灰度值方差小于特定阈值σVF的所有子窗口都丢弃。这个阈值定义为初始目标模型中方差的一半，因为方差会根据目标而改变。为了减少计算时间和内存使用量，通过积分图像计算每个子窗口的方差。为了计算每个子窗口B 的方差，需要使用两个积分图像。其中一个是位置( x,y )处的积分图像I′，包含了图像中点（1，1）和( x,y )之间的所有像素值的总和，可以表述为：

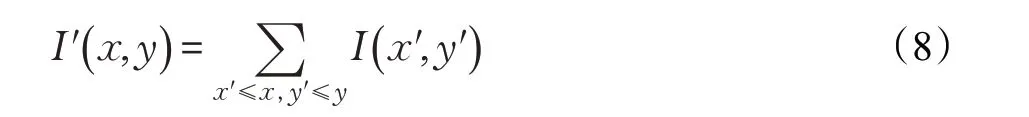
另一个积分图像I″表示图像I 的平方值，表示如下：

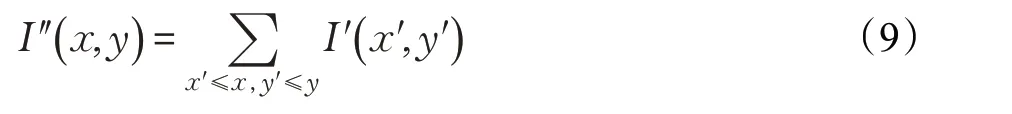
使用这些积分图像，子窗口B 的方差可以表示为：

其中n 是图像中的像素数。

4.2 集成分类器

通过方差滤波器过滤掉背景以后，执行探测过程的第二步，即采用基于随机化的集成分类器，通过比较几个像素的强度值对像素进行分类。此阶段的输入是一组通过方差滤波器输出的子窗口。对于每个候选子窗口，计算一个概率，用于表示子块是否对应于正确标签。如果概率值小于0.5，则子窗口被拒绝。

集成分类器由M 个子分类器组成，每个子分类器都执行像素的强度值比较。在算法开始时，从均匀分布中随机提取像素的位置，并在跟踪目标期间固定像素的位置。每个子分类器的输出表示为：

其中，d1和d2是图像I 中的随机位置。最后，使用式（12）对每个子分类器的概率进行平均，当平均概率大于0.5时，集成分类器将子窗口分类为目标对象：

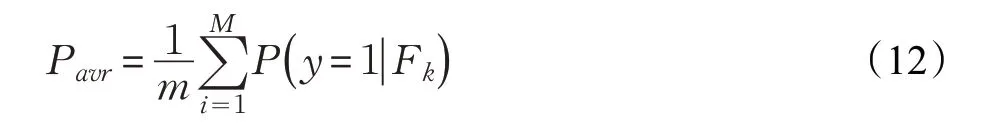
4.3 模型匹配

在通过分类器对目标像素进行分类后，执行探测器的最后一步，即使用模型匹配方法搜索目标。模型匹配过程会在探测图像与目标模型之间进行逐像素的比较，当两者相似性大于特定阈值时，判断该探测图像为探测器找到的目标模型。然后通过式（7）来更新MST 中的目标模型，获得尺度更新过的新目标模型

为了减少计算时间，将输入子窗口的大小调整为MtNt。在所提出的方法中，通过归一化相关系数(NCC)来测量相似性。子窗口T1和T2之间的NCC 表示如下：

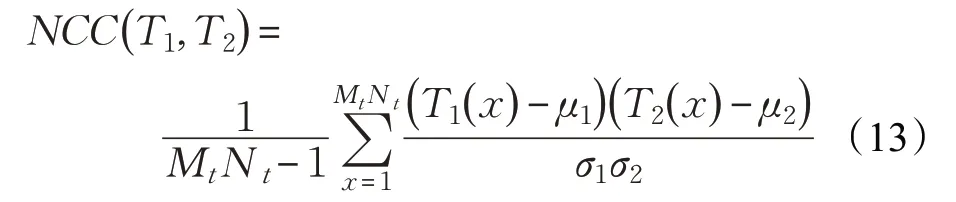
其中μ1和μ2,σ1和σ2分别是T1和T2的均值和标准差。使用NCC，两个子窗口之间的距离计算如下：

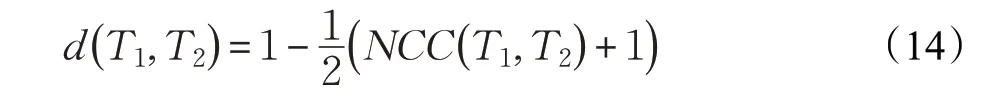
在跟踪期间，更新正类和负类的标准化模型。给定输入子窗口Tin，正类和负类的距离表示为：

其中T+和T-分别是正类和负类的集合。那么，模型匹配概率的定义为：

该概率表示子窗口是否包括目标，如果概率大于特定阈值σTM，则确定相应的子窗口属于目标。

4.4 在线学习

P-N学习方法是一种半监督学习方法，其使用两种类型的约束从未标记数据中提取示例以增强训练集。一个是P 约束，它可以识别假阴性示例，然后将它们放入一个正类训练集中。另一个是N 约束，它可以识别假阳性示例，然后将它们添加到负类训练集中。P-N学习的目标是通过在标记数据中的学习分类，并将未标记的数据进行分类以扩充标记数据集。

为了学习分类器，使用了检测到的目标的反常子块。P 约束的功能是找到目标的新外观，以便于探测器的泛化。它基于跟踪器结果附近的子窗口将具有正标签的事实来搜索示例。也就是说，P 约束用于分类高度重叠的子块。相比之下，N 约束的目的是在背景中发现杂乱像素点，以便于探测器的目标检测。

5 基于粒子滤波的位置估计

由于传统MST 只会锁定领域内的局部最大值，当遇到大面积遮挡时，MST 锁定的目标位置会与真实位置有偏差。这个偏差会随着遮挡视频帧的增加而持续扩大，以致最后丢失目标。为此，在发生严重遮挡时，本文启动粒子滤波器，用来估计遮挡时的目标位置。在遮挡过后，根据所估计的位置，使MST 能够快速搜索到目标。

粒子滤波器能够为发生遮挡时的目标跟踪提供很强的鲁棒性，这是因为它既不受限于线性系统，也不要求噪声服从高斯分布。粒子滤波中，将目标可能的位置是真实位置的概率作为粒子。前一帧中的所有粒子会以状态传递函数的形式转换到当前帧，虽然粒子位置和权重都发生变化，但它仍能提供最近似实际位置的目标位置。

为了估计系统的后验状态，定义一个目标模型，如下所示：

式中，fm-1为目标状态的非线性函数；wm-1为白噪声序列，代表状态预测的不确定性。当前时间m(m ≥1)的在线离散预测zm由下式确定：

式中，hm为非线性函数，um为零均值的白噪声序列，表示预测中的误差。

粒子滤波的迭代过程分为两个部分：（1）预测；（2）更新。

在预测阶段，利用系统模型及m 时刻的初始概率密度，通过积分运算获得m-1 时刻的概率密度，表达式如下：

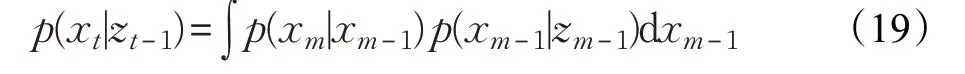
其中，zm={ }zi:i=1,2,…,m 为给定的在线观测序列。

在更新阶段，在给定先验概率密度p(x1|z0)≡p(x1)、状态函数形式(f)、外观模型(h)以及最终预测时刻的情况下，每一时间步长处估计后验密度p(x0:m|z1:m)表达式如下：

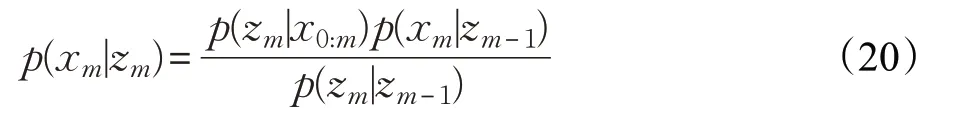
对于目标跟踪的应用，需要从初始给定的概率密度p(x1)中获取N 个观测样本。为了获得一致性的粒子观测值，需要为这些粒子样本分配一致性权重，表示如下：

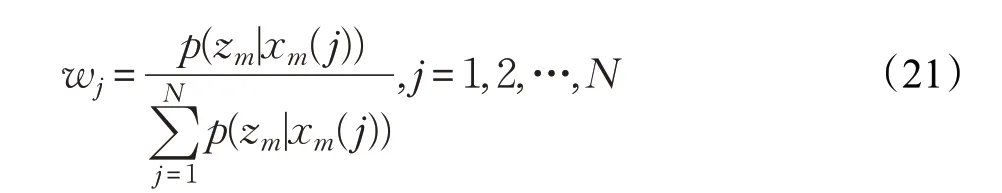
由于假设目标状态变化为马尔可夫链，则后验概率可以描述为：

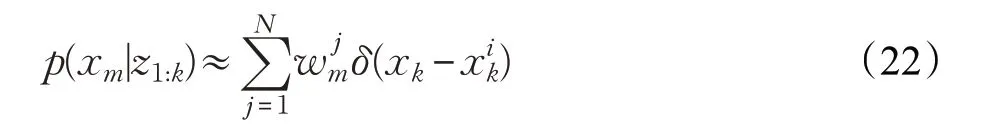
式中，δ(⋅)表示狄拉克δ 函数。

本文提出的实时目标跟踪方法的伪代码如算法1所示。

算法1 提出的目标跟踪算法

初始化：

1. 通过式（1）计算目标模型q̂，并初始化位置y0；

2. 初始化参数；

3. 基于在第一帧中的目标选择进行学习；

执行：

6. 确定是否目标跟踪成功

则通过式（16）计算跟踪器输出的子块和正类样本集中子块的相似性STM（模型匹配概率）；

如果(STM＞σTM)

则跟踪器提供正类和负面图像子块，并执行学习。

否则

通过粒子滤波，基于跟踪器中的目标位置来估计位置。

否则

通过粒子滤波预测目标的位置；

通过式（16）计算探测器探测的子块与正类样本集的相似性STM；

如果(STM＞σTM)

通过粒子滤波估计位置和尺度；

为跟踪器更新目标模型；

否则

通过粒子滤波预测目标的位置；

7. 返回到第4步骤；

输出：

估计的目标位置和尺度。

6 实验及分析

6.1 实验设定

实验使用的测试视频序列来自PETS 2009数据集，这些视频中包含了遮挡、背景杂乱和外观变化在内的各种环境。实验在具有英特尔酷睿i7-3.40 GHz CPU，8 GB RAM PC机上的MATLAB上编程执行。

使用这些视频序列进行性能评估，并与一些基于MST的改进方法进行比较，分别为经典MST跟踪器、文献[10]提出的结合自适应背景加权直方图的BWH-MST方法、文献[12]提出的卡尔曼滤波与SOAMST相结合的算法（K-SOAMST）。MST算法使用基于颜色直方图的目标模型迭代估计对象的位置。BWH-MST 使用背景加权直方图解决了背景复杂的问题。K-SOAMST算法改善了MST 在尺度估计和方向估计等方面存在的问题，并结合卡尔曼滤波提高对遮挡的应对能力。

对于基于均值漂移框架的跟踪器，使用RGB 颜色空间，并且每个通道被均等地分成16 个区域以表示目标和候选，而且都应用Epanechnikov内核。对于本文提出的算法，Bhattacharyya 系数的阈值σVF（用于确定跟踪是否成功）设置为0.65。粒子滤波器中的粒子数量设置为30。对于探测器，相似性的阈值σTM定义为0.6。用于更新目标模型的β 设置为0.9。这些值是通过多次实验结果确定的。

6.2 性能指标

为了评估跟踪算法性能，使用两个性能指标。第一个是中心位置误差（CLE），它可以测量估计物体的中心位置与实际数据之间的误差，定义如下：

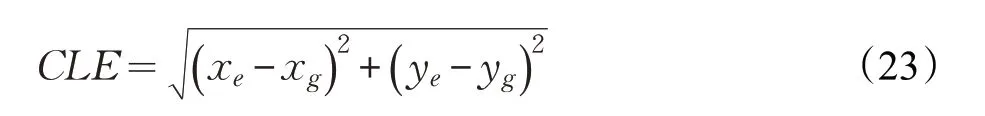
其中，xe和ye表示跟踪结果的中心位置，xg和yg表示实况数据的中心位置。

第二个性能指标是成功率（SR），定义如下：

其中，Re是跟踪结果的边界框，Rg是实况数据的边界框。如果SR 大于0.5，则判定跟踪结果为成功。

6.3 性能评估

为客观地评估所提出的算法与其他基于均值漂移的跟踪算法（MST、BWH-MST 和K-SOAMST），选择了四个具有挑战性的视频序列来构建测试数据集，分别为Ball序列，Car1序列，Car2序列，和Person1序列。其中，Ball 序列存在目标快速移动，Car1 序列包含了遮挡情况，Car2序列包含了尺度变化情况，Person1序列存在光照变化。

图2 举例显示了在Car1 序列和Car2 序列上各种算法的跟踪结果。图2（a）显示了在存在完全遮挡情况下的跟踪情况。在完全遮挡之前，每个跟踪器都可以估计目标位置。然而，在经过完全遮挡之后，只有本文算法可以跟踪目标。K-SOAMST 也具有处理遮挡的能力，但是在该视频序列中，汽车目标移动较快，非线性较强，导致卡尔曼滤波的性能下降。在本文方法中，粒子滤波可以很好地应对非线性和非高斯环境，为此能够纠正跟踪过程。在图2（b）的序列中，目标发生了尺度变化。在这个视频序列中，所有算法都可以跟踪目标，其中本文算法和K-SOAMST 算法的尺度估计准确性较高，能够自适应调整目标的尺度。这是因为本文算法中融入了用于尺度调整的探测器过程。

图2 各种基于MST算法的跟踪结果

各种算法在4个视频序列上的平均CLE和SR性能指标如表1和表2所示。

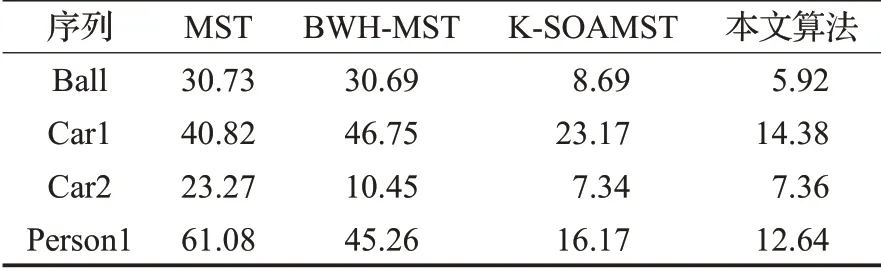
表1 平均中心位置误差（CLE）

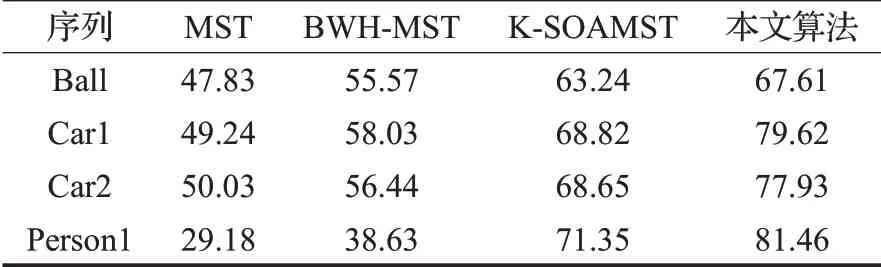
表2 平均跟踪成功率（SR） %

从表1 和表2 所示的结果可以看到，本文算法都获得了最佳结果。对于Ball 序列，目标快速移动，使得它在连续帧之间的位移很大。虽然MST算法无法跟踪目标，但本文算法在此序列上表现良好。这是因为粒子滤波器基于先前的目标运动轨迹，精确地估计目标位置，从而减少目标在连续帧之间的位移，这使得MST 算法能够成功地跟踪对象。此外，当MST 算法无法跟踪对象时，探测器会找到目标位置并重新初始化MST 算法。在Car1 序列中，目标在15 帧中经历完全遮挡。本文算法在目标重新出现后表现良好，这是因为粒子滤波器在目标完全遮挡时预测目标位置，并且当目标再次出现时，MST 算法可以使用所预测的目标位置成功跟踪目标。在Car2 序列中，目标的尺度变小。本文方法在探测器的帮助下估计目标尺度。在Person1 序列中，当目标模型由于光照变化而改变时，MST和BWH-MST算法无法跟踪目标。

另外，各种算法每帧目标跟踪的平均计算时间如表3所示。其中，基于MST的跟踪器最显著的优势在于可以在较短时间内跟踪目标，为此各种方法的计算时间都不是很高，都在15 ms 以内。其中，传统MST 算法计算时间最短为3.85 ms。尽管所提出的算法包含探测和学习过程，但本文在探测过程中调整了输入子窗口的大小，使其计算速度并没有增加太多，为11.55 ms。

表3 跟踪算法的执行时间

上述实验结果表明，本文算法不仅具有良好的跟踪性能，且所需要的计算时间也较少，因此可以成功地应用于实时跟踪应用。这是因为本文提出的算法结合了传统MST 算法和粒子滤波算法，具备了MST 算法运算量少，跟踪速度快，以及粒子滤波算法的鲁棒性高和抗干扰、抗遮挡能力强的优点。

7 结语

本文提出了一种基于改进MST 的实时跟踪算法，将MST 与粒子滤波器和基于在线学习的探测器相结合，这使得算法能够在包含完全遮挡或对象重新出现的复杂环境中跟踪目标，且可以使用探测器估计目标的尺度。与具有挑战性的视频序列上的比较表明，所提出的算法在准确性方面表现良好。

但是，本文算法仍有一些局限性。例如，在发生遮挡时，本文假设目标以相同的速度移动。为了解决这个缺点，在今后的工作中将考虑引入一个基于复杂运动模型的非线性滤波框架。