一维量子卷积计算

闫茜茜，王鹏程，刘兴云

湖北师范大学 物理与电子科学学院，湖北 黄石435002

1 引言

作为一种新颖的计算模型，量子计算具有两个突出的特点：其一量子态的叠加和纠缠等性质可以完成并行计算处理加快数据的计算速率，具有代表性的是肖尔（Shor）大数分解算法[1]、波色取样[2]、格罗夫尔（Grover）搜索[3]、量子退火算法等。其二n 个量子比特有2n个状态即n 个量子比特可以存储2n位信息，提高了信息存储空间，例如运用在量子图像处理中，量子图像表示（QIMR）起着关键的作用[4-8]。

卷积神经网络在数据信息处理方面有助于改进机器学习，例如在物体分类[9-13]、目标检测[14-16]等领域已取得不错成就。随着社会的发展，卷积神经网络的计算数据愈加庞大，导致计算速率愈加缓慢，量子计算相比于经典计算具有更高的优势[17-18]，因此需要借用量子计算的原理或概念计算卷积，以提高卷积神经网络计算速率。许兴阳、刘宏志[19]通过给出卷积算术线路定义，进而设计出了量子门组卷积神经网络模型（QGCNN）；Cong I 等[20]引入并分析了受机器学习启发的量子线路模型Quantum Convolutional Neural Networks（QCNN），证明了QCNN 可以准确识别与一维对称保护拓扑阶段相关的量子状态及对给定的未知错误模型优化的量子错误校正方案，其性能优于现有方法；Henderson M等[21]研究了在标准的卷积神经网络体系结构中添加量子卷积层，来设计量子卷积神经网络。

以上文献通过经典的卷积神经网络模型和量子计算的特性，来设计搭建量子卷积神经网络，并通过不同的实验方法验证量子卷积神经网络的高效性，但是在文献中只是借用酋算子搭建简易线路，没有设计出详细的量子卷积线路，进而也没有完整的量子卷积神经网络量子线路模型。为了研究通用量子卷积神经网络的量子线路，使量子计算与卷积神经网络完美结合并且发挥两者最大的优势，根据Yao等[8]和Cong I等[20]文章中的计算原理，将一维信息编码为量子态，受控非门及Hadamard门完成量子卷积计算量子线路搭建，设计出了在任何实验中通用的量子卷积线路模型。

2 量子信息处理

最近大量研究中，将量子计算与数字图像处理相结合对于解决实际图像处理应用中的高精度和高实时性问题非常有效。Venegas-Andraca S E 等[5]提出一种基于“qubit lattice”的存储，即对于一个输入图像，其中每一个像素点都有一个qubit 来表示，因此需要至少2n比特的存储。Le P 等[6]提出一种FRQI 模型，该编码方式将像素值和像素位置通过量子态张量积的形式进行了关联，采用1 个量子比特编码像素值，颜色信息编码在概率幅中。Zhang Y 等[7]提出了一种NEQR 模型，同样通过张量积的形式将像素值和像素位置进行了关联，不同的是采用了d 个量子比特编码像素值，灰度信息编码在基态中。Yao 等[8]提出了QImR 模型，该模型用于将2D 图像编码为量子纯态，图像的像素值由量子态的概率幅表示，图像的像素位置由量子态的基态表示。

运用到一维信息处理中，采用QImR模型编码方式将信息的信息熵由量子态的概率幅表示，信息熵的位置由量子态的基态表示。一维信息展开得到一个列向量，将这个列向量映射为含有L=2l个量子比特的量子态

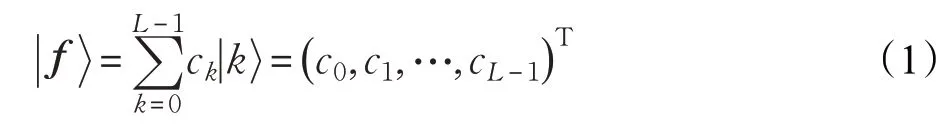
3 一维量子卷积计算

由经典卷积计算过程知，两个向量卷积的结果仍然是一个向量，以短向量长度向长向量截取对应长度进行内积计算，之后保持长向量不变短向量进行一步移位操作，直到短向量最后一个元素与长向量最后一个元素对齐并计算其内积，最终得到卷积结果向量。卷积计算步骤可归纳为相乘、求和、移位，因此在用量子计算方法设计量子卷积线路模型时也有相同的计算步骤。如图1所示为量子卷积计算流程图，首先将经典信息进行编码处理转化为量子信息，量子信息量子态输入到量子线路模型中进行卷积计算，量子态张量积完成相乘过程，概率幅置换完成移位过程，加法计算完成求和过程，最后进行量子态提取得出卷积结果。

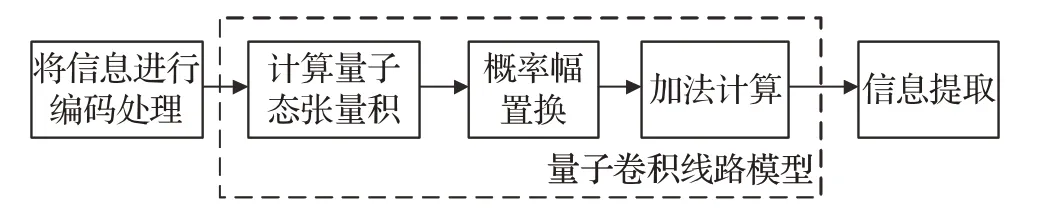
图1 量子卷积线路模型流程

3.1 计算量子态张量积

通过采用上述编码方式，将经典信息P1、P2分别编码为含有m-qbit、n-qbit 的 量 子 态其中M=2m、N=2n，若m ≥n 则以信息P2为卷积核，对信息P1进行卷积计算。在希尔伯特空间H1和H2中，量子态进行张量积运算即：

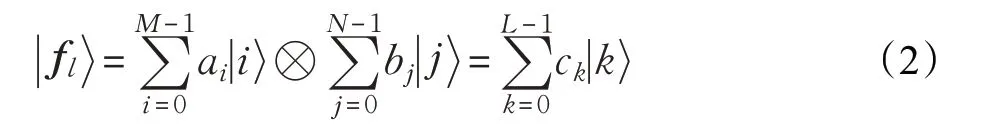
3.2 概率幅置换QL

QL运算是一个含有L=2l个量子比特的概率幅置换运算，由通用量子门多位受控非门（CNOT）构成。CNOT 分为1 型受控非门和0 型受控非门，包括控制量子比特和目标量子比特，1型受控非门中当控制量子比特全为态时，目标量子比特由或由，0 型受控非门当控制量子比特全为0 态时才对目标量子比特起作用。如表1所示为对计算基矢的作用，其中双量子比特门受控非门作用为，三比特受控—受控非门（CCNOT）称为Toffoli门，作用为其中a、b、c=0 或1，⊕表示以2为模的加法。

表1 通用受控非门

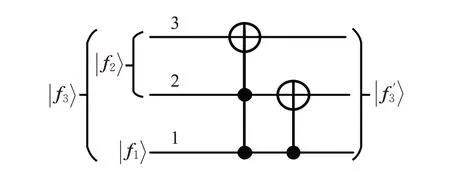
图2 3-qbit Q8 量子置换线路

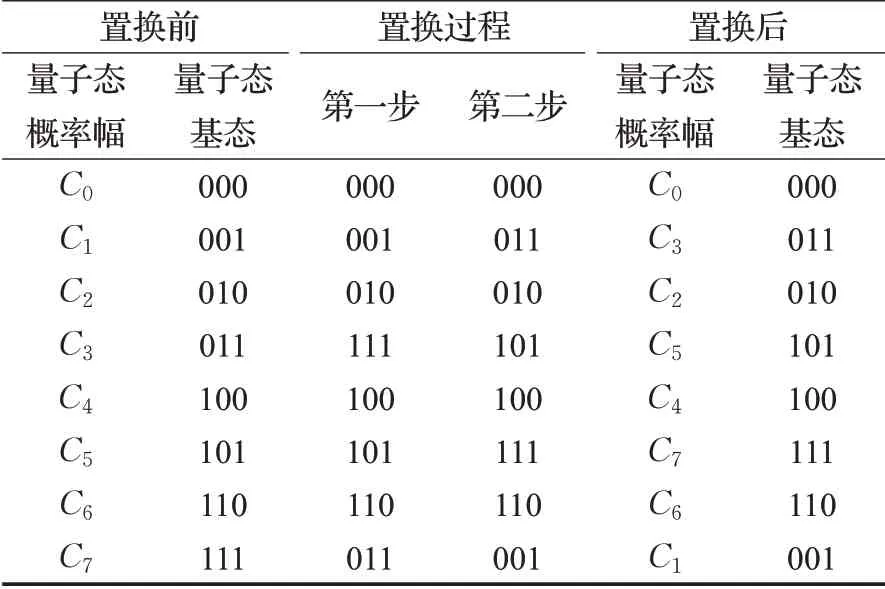
表2 Q8 线路具体置换方法

3.3 加法运算

单量子比特H 门的定义为：

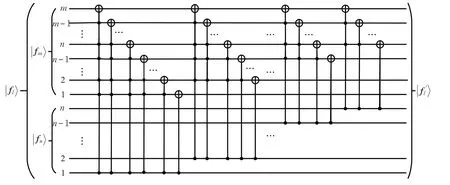
图3 QL 量子线路置换图

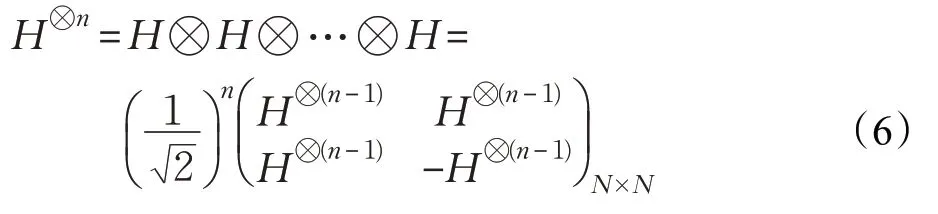
则

IM×M⊗H⊗n矩阵中，只有第1 行、第N+1 行、…、第(M-1)N+1 行相应位置为1，其余行相应位置都是1、-1穿插出现。如对量子态的1个量子比特执行H 门，对剩余的量子比特即量子态的2个量子比特执行单位矩阵，I4×4⊗H 矩阵表达式为：

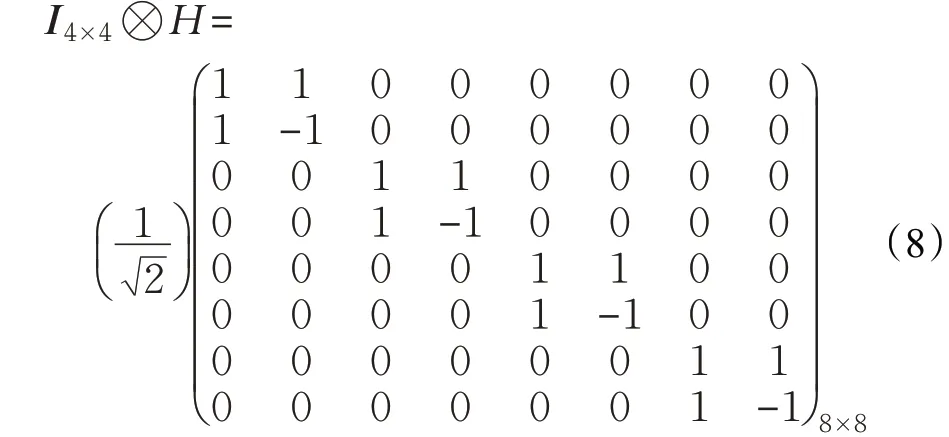
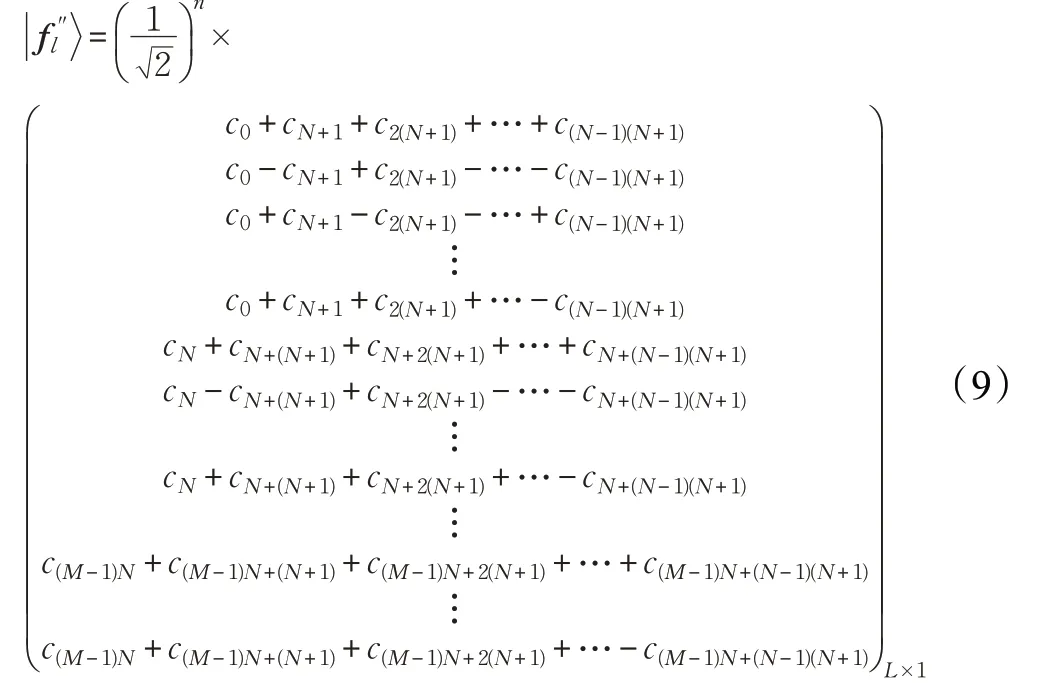
3.4 输出结果

当对量子态进行提取的瞬间，量子态坍缩到一个具体的态上，此时的卷积结果也将被破坏，Cong I 等[20]表明测量放在QCNN 线路中池化层和最后结果的输出部分，用于确定量子比特受控旋转及固定数量的输出量子位，因此在以后的量子卷积神经网络的量子线路模型设计中，无需对其量子卷积计算部分进行结果提取直接进行后续操作即可。如对量子态的量子比特进行结果提取，当此量子比特的提取结果为时，得到卷积结果由矩阵可知，一维量子卷积计算结果为矩阵当中概率幅全相加的行，即第1 行、第N+1 行、…、第(M-1)N+1行，因此需要对初始量子态的n 个量子比特进行提取，当n 个量子比特的结果为时，即卷积结果g 矩阵形式为式（10），进而得出量子卷积线路模型，如图4所示。

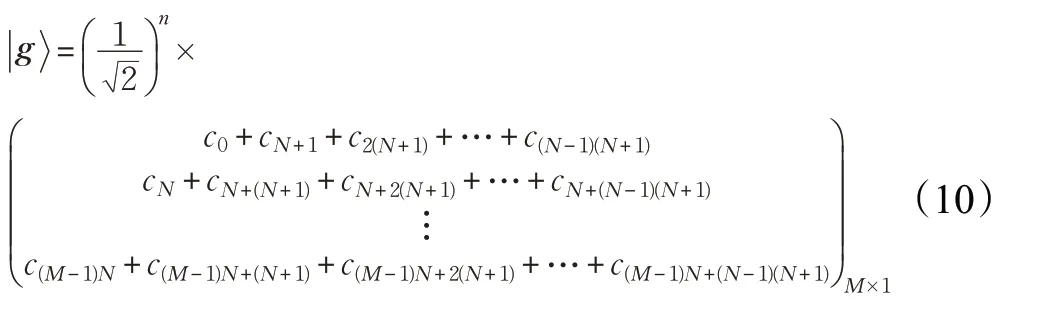
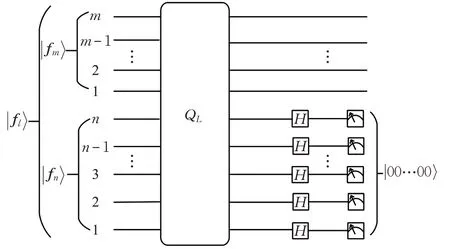
图4 一维量子卷积量子线路模型

4 结论

任意多量子比特运算线路都可以分解为双量子比特门或三量子比特等一些单量子比特门，通常这些简单的量子门数量表示对量子运算计算复杂度的估计。根据量子卷积算法线路模型可知，以n-qbit 量子态为卷积核对以m-qbit 的量子态为目标信息进行的量子卷积计算中，总的量子门数满足，故量子卷积计算总的计算复杂度不超过O(n2)。

重点研究了在量子叠加态形式中，通过设计量子卷积线路模型来进行卷积计算，概率幅置换完成经典卷积计算中的移位过程，加法计算完成经典卷积计算中的对应相加计算过程。在存储上，经典计算需要2l比特，量子计算需要l 量子比特即可；在计算上，经典计算是移位相乘累加运算，量子计算是酉算子的演化。因此可以根据量子并行计算的特点计算卷积，并且该一维量子卷积算法大大减少了卷积计算步骤，提高了计算速率，增加了信息的存储空间，为量子计算与人工智能的结合提出新的解决思路。