Helmert方差分量估计在GPS/GLONASS/BDS组合单点定位中的应用

代 阳

（安徽理工大学测绘学院，安徽 淮南 232001）

北斗三号全球组网空间星座部署任务圆满完成，标志着我国北斗服务范围由区域迈向全球，同时也意味着全球卫星导航系统（Global Navigation Satellite System，GNSS）的多系统合作与兼容变得更加成熟[1]。目前主流的卫星导航系统分别为中国开发的北斗系统（BeiDou Navigation Satellite System，BDS）、俄罗斯开发的格洛纳斯系统（Global Orbiting Navigation Satellite System，GLONASS）与美国开发的全球定位系统（Global Positioning System，GPS）。相比较于单系统定位，多系统组合定位能够提供更多的可视卫星，完善星座的几何结构，适用于更广泛的时空领域[2]。同时在算法方面，多系统组成的卫星观测数据能够削弱单系统定位中的系统误差，并提供适量冗余数据，可有效避免系数方程的病态性。因此，GPS/GLONASS/BDS 多系统组合定位在定位服务中的地位越来越重要。

在多系统组合定位中，伪距单点定位模型因为测量方式简单、实时性强被广泛应用于导航定位服务中。但是在进行多系统伪距单点定位时，由于GPS/GLONASS/BDS 系统间观测噪声不同、轨道布设不一，提供的观测数据精度存在差异，因此，单纯地将各个系统的观测数据归为一类，系统间采用等权模型定权，会导致随机模型不精确，降低定位精度[3]。如何精化系统间权阵，是提高多系统单点定位精度的关键问题。

常用于系统间定权的方法有二次无偏估计法、信噪比定权法、等权模型与Helmert 方差分量估计模型等。其中Helmert 方差分量估计模型被广泛应用于卫星定位领域。Helmert 方差分量估计模型通过预平差得到的残差改正数，估计出各个系统的验后单位权方差，从而对各个系统定权，降低观测质量较低系统的权重，以达到提高精度的目的[4]。段举举等在GPS/GLONASS 组合单点定位中，采用Helmert 模型对GPS、GLONASS 两个系统进行定权，有效地提高了点位精度[5]。张广汉等在GPS/BDS 伪距单点定位中，采用Helmert 方差分量估计进行定权，认为系统间合理权比为1∶1[6]。刘天骏等在GPS/BDS 组合定位中，将卫星类型分为GPS/GEO/MEO/IGSO 类，将指数加权与Helmert 方差分量估计结合，有效地提高了静态与动态单导航定位的精度[7]。在现在的卫星导航定位服务中，随着GPS，GLONASS，BDS 系统不断地完善与发展，其应用领域也越来越广泛。因此，确定GPS/GLONASS/BDS 系统间的权比有着重要的意义。

1 三系统伪距单点定位的函数模型

1.1 三系统伪距单点定位原理

伪距单点定位通过导航电文推算各个卫星实时的在轨位置、卫星钟差改正，并利用伪距码测算各个卫星到接收机的空间距离，进而根据空间交会原理推算接收机此刻的位置。

由于误差无可避免，在利用最小二乘平差得到的结果会受到接收机钟差、卫星钟差、电离层误差、对流层误差、多路径效应等的影响。若忽略它们的影响，定位结果精度大大降低，定位偏差甚至会达到十几米。因此，采用卫星实时播发的星历文件改正卫星钟差，采用无电离层组合、Klobuchar模型等消除电离层误差影响，并采用Saastamoinen模型、Hopfield 模型等改正对流层误差[8]。接收机钟差难以对建立数学模型进行拟合，通常将其与接收机的三维空间坐标一起作为参数通过最小二乘进行解算。而多路径效应受测站周边环境影响，因此通常将测站架设在空旷、反射物较少的环境下。

不同于单系统，GPS/GLONASS/BDS 伪距单点定位不但需要考虑上述方面影响，同时需要统一GPS，GLONASS，BDS 3 个系统的时间基准与空间基准[9]。并且接收机在接收3 个系统的数据时存在硬件延迟偏差，不同的系统之间存在着时间偏差，因此GPS/GLONASS/BDS 伪距单点定位需要计算额外的GLONASS，BDS 相较于GPS 的系统间时间偏差参数，观测卫星数不得少于6 个。

1.2 三系统伪距单点定位观测方程

GPS/GLONASS/BDS 伪距单点定位的数学模型为

式中：G为 GPS 卫星；R为 GLONASS 卫星；B为BDS 卫星；j为对应的卫星编号；ρ为伪距观测值；r为接收机到卫星的几何距离；c为光速；dtr与dts分别为接收机钟差与卫星钟；为GLONASS，BDS 相较于GPS 的系统间时间偏差。Δion为电离层误差；Δtrop为对流层误差；Δmul为多路径误差；ε为观测噪声。

将式（1）线性化后，可得

式中：V为GPS，GLONASS，BDS 系统伪距观测值的改正值； [x0y0z0]为站点的近似三维坐标，通过最小二乘平差多次迭代得到；为卫星坐标，i 可取G，R 或B，通过导航电文求得；dx，dy，dz为站点坐标在x，y，z 方向的改正数；L为对应各个系统的残差项。

2 三系统组合单点定位的随机模型

卫星观测数据的质量，受到卫星系统误差、轨道精度、观测噪声及卫星与观测站之间的相对位置影响。如果将每颗卫星的观测数据简单地杂糅在一起，忽略各个卫星观测精度差异，做等权处理，势必会降低定位解算的精度。因此，根据各个卫星观测质量的差异，降低观测质量差的卫星权值，提高观测质量好的卫星权重，能够有效地提高定位解算精度。目前常用的定权模型从两个方面出发。同一系统内，采用高度角模型且信噪比模型定权，前者数据容易获取并计算简单，被广泛使用。不同系统之间，通常采用等权模型、Helmert 模型进行定权。等权模型考虑不同系统的整体观测质量水平相当，系统间的权比均为1，系统内部采用高度角定权；而Helmert 模型考虑到不同系统间的轨道精度差异、星历精度差异等，通过验后方差估计各个系统的单位权方差，系统内部采用高度角模型。

2.1 高度角定权模型

在同一系统内部，卫星的观测数据质量受卫星高度角影响，呈正相关趋势。在卫星沿着轨道运行时，不同卫星与测站的相对位置不同，信号传播路径存在差异。当卫星的高度角较低时，测距码信号传播路径增加，期间受大气对流层及电离层误差影响较大；并且，由于测站与卫星的相对高度较低，易受周围反射源影响，多路径效应加大。当卫星的高度角增高时，受各方面误差影响较低，且卫星的几何精度提高。为了降低卫星高度角对定位结果的影响，通过设置截止高度角与高度角模型定权改善系统内部观测值的精度。对于高度角很低、观测质量差的卫星，设置高度截止角，将高度角低于阈值的卫星数据的权值设置为0。而高于阈值的卫星，根据卫星的观测值精度与高度角呈正相关的规律，采用高度角模型定权。目前，高度角定权模型常使用的函数为三角函数高度角模型，其表达式[10]为

式中：i为对应卫星的编号；P为该卫星观测值的权值；φi为第i 颗卫星的高度角；α为截止高度角，通常设置为15°。

2.2 Helmert 方差分量估计

Helmert 方差分量估计模型在GPS/GLONASS/BDS 系统间定权的步骤[11]有 5 步。

1）系统间的初始单位权方差均为θG=θR=θB=1，同一系统内部定权方式按照高度角定权模型通过高度角方式定权。

2）通过最小二乘法，解算接收机的近似坐标，并计算伪距观测值的改正数V。

3）通过严密Helmert 方差分量估计，分别计算GPS，GLONASS，BDS 的单位权方差，具体公式为

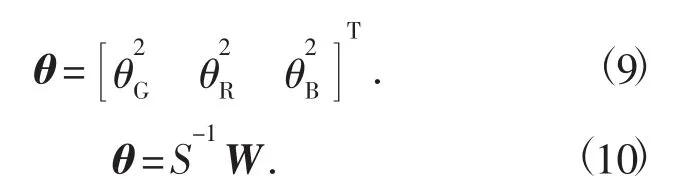
式中：A为伪距单点定位的系数矩阵；P为观测值权阵；n为GPS，GLONASS 与BDS 对应的卫星个数；N，S，W 均为中间变量。

4）利用单位权方差θ，更新各个系统的权阵为

3 算例及精度分析

3.1 实验数据

本文实验数据采集于安徽理工大学本楼上观测站点CORS1，CORS2 与CORS3，接收机板卡型号均为 BD980，天线类型均为 AT300，能够接收GPS，GLONASS 与BDS 的双频观测数据。数据采集时间段为 2019年9月30日21﹕58﹕30—10月1日 00﹕38﹕30，采样间隔为1 Hz，共9 600历元。卫星的截止高度角设置为15°，接收波段为L1/L2 波段。该cors 站点的真实坐标由长期静态相对定位获得。

3.2 实验案例

为了验证Helmert 方差分量估计在GPS/GLONASS/BDS 组合伪距单点定位中的可靠性与稳定性，笔者根据实验数据，分别采用等权模型与Helmert 方差分量估计模型进行对比实验。实验具体步骤如下。

1）在采集的三系统卫星数据中，通过截止高度角与信噪比设置，去除观测质量较差的卫星。

2）通过筛选后的卫星观测文件与导航电文，确定每个历元下各个卫星的轨道位置及观测方程。

3）设置系统间初始权比均为1，并通过最小二乘法，解算接收机的近似坐标。

4）根据实验步骤，计算在Helmert 方差分量估计定权下的定位结果，并统计解算坐标在x，y 与z方向的点位偏差。

5）计算系统之间采用等权模型定权，系统内部采用高度角模型定权下的定位结果，并统计解算坐标在各个方向上误差。

根据上述实验步骤，分别统计CORS1，CORS2与CORS3 观测站在两种定权模型下的每个历元的解算结果。在此笔者仅列出CORS1 站点在x，y 与z 方向上的点位偏差，见图1～3。

图1 在两种定权方式下的x 方向下的误差

图2 在两种定权方式下的y 方向下的误差

图3 在两种定权方式下的z 方向下的误差

由图1～3 可知，采用Helmert 方差分量估计对GPS/GLONASS/BDS 系统间进行定权，在x，y 与z方向上的定位结果明显优于等权模型定权下的结果，在各个方向的误差更小；在2 000～5 000 历元期间，外界环境发生改变，观测条件变差，采用等权模型定权下的定位误差在x，y 与z 方向上明显变大，甚至部分历元产生粗差，而采用Helmert 方差分量估计定权下的解算结果虽然受到影响，但每个历元的定位误差均小于等权模型，呈现稳定的趋势，并未产生粗差；相较于等权模型，Helmert 模型在x，y 方向上的改善结果较明显，在z 方向的改善结果较小。

在等权模型与Helmert 模型定权下，统计CORS1，CORS2 与CORS3 测站定位解算误差统计结果，见表1。

由表1得，在 CORS1，CORS2 与 CORS3 测站下进行多系统伪距单点定位，采用Helmert 模型定权下的解算结果在x，y，z 方向偏差及点位误差均小于等权模型定位结果；在这3 个站点下，Helmert 方差分量估计均在x 方向上改进程度最大，最高改善了0.484 m；y 方向次之；z 方向改善程度较弱，但最低也改善了0.645 m。综上所述，与等权模型相比，Helmert 模型定权下在不同站点的解算结果精度更高，可靠性与稳定性更强。

表1 不同站点在不同定权方式下的方向偏差与点位误差 （m）

4 结论

本文针对GPS/GLONASS/BDS 三系统组合伪距单点定位中如何定权、提高精度的问题，提出了采用Helmert 方差分量估计确定系统间的权比。通过实测数据分析，最终验证了Helmert 方差分量估计应用于伪距单点定位的可靠性与稳定性。实验结果表明，与等权模型相比，采用Helmert 模型解算的结果在x，y 与z 方向的精度更高。并且，在受到外界因素的影响下，等权模型解算结果受到影响波动较大，而Helmert 模型解算结果更加稳定，不易受到影响。综上所述，在GPS/GLONASS/BDS 三系统组合伪距单点定位中，采用Helmert 方差分量估计精化权阵，能有效提高定位解算的精度与可靠性。

本文仅对GPS/GLONASS/BDS 三系统下伪距单点定位的随机模型进行讨论，并未考虑到GPS/GLONASS/BDS 三系统下相对定位中随机模型如何确定的情况，这将是作者的下一步研究方向。