对2019年高考理综新课标卷Ⅰ第21题的赏析与教学启示

胡小波

(泰州市姜堰区娄庄中学,江苏 泰州 225506)

图1

在星球M上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示．在另一星球N上用完全相同的弹簧,改用物体Q完成同样的过程,其a-x关系如图中虚线所示,假设两星球均为质量均匀分布的球体．已知星球M的半径是星球N的3倍,则

(A)M与N的密度相等.

(B)Q的质量是P的3倍.

(C)Q下落过程中的最大动能是P的4倍.

(D)Q下落过程中弹簧的最大压缩量是P的4倍.

1 试题分析

命题意图： 题目主要考查的知识点是:万有引力定律应用、牛顿第二定律、胡克定律、力和运动、功能关系、能量转化与守恒及a-x图像的意义．主要考查的能力有:图像的理解能力(截距、面积等意义)、推理能力、综合分析能力等．

试题特点： 从新课程标准角度看,该题通过小球在弹簧上的运动借助a-x图像的显现体现了对学生模型建构、科学推理等科学思维素养的综合考查,对学生运动与相互作用观、能量观等物理观念素养有较高的考查,与新课程标准强调学生科学思维、物理观念等核心素养的培养相呼应;从知识与能力角度看试题将万有引力定律应用、弹簧弹力作用下的力与运动、牛顿运动定律、胡克定律、功能关系、机械能守恒、能量的转化与守恒等看似独立无序的核心知识借助a-x图像巧妙的串联起来,压缩成一道经典的动力学问题,综合性强,对学生的能力要求较高,显示出较好的区分度,以达到选拔优质人才的目的．

解题技巧： 星球密度的计算、在弹簧上运动的两物块质量比较和最大动能的关系以及最大压缩量的比较这种种物理量的关联分析都隐藏在a-x图像中,将物块在竖直放置的弹簧上的压缩弹簧的运动这一具体情境与a-x图像巧妙对应起来,便是解决这道题的核心思想所在．

2 解题方法

2.1 MN两星球密度的比较

众所周知,天体密度的计算是建立在牛顿的万有引力定律基础上,其核心方法有两类:一类是根据天体表面的重力加速度g和天体作为一均匀球体的半径R求解,原理是地面上的物体所受星球的万有引力等于物体的重力,从而求出天体的质量M,再据密度公式求出天体密度即可;第二类是利用天体的一颗卫星(或行星)求解,通常是已知卫星的线速度、角速度、周期、向心加速度和轨道半径(分别记为v、ω、T、a、r)中的任意两个参数(不能同时是ω、T)再加上天体的半径R便可计算出天体的密度,原理是天体对其卫星的万有引力提供向心力求出天体质量M,再用密度公式求其密度．综合上述方法和题目具体情境该题应当是用第一种方法．

当物块在弹簧上由静止向下运动时,便逐渐压缩弹簧,在开始运动的瞬间,弹簧处于原长,此时物块运动的加速度即为所在星球表面处的加速度．

由图像易知,

对P而言,当x=0时,加速度

a=gM=3a0.

(1)

对Q而言,当x=0时,加速度

a=gN=a0.

(2)

由(1)、(2)得星球M和星球N表面的重力加速度关系为

gM=3gN.

(3)

对星球M和星球M表面的一个质量为m的物体,由万有引力定律等于重力得

(4)

解得星球M的质量为

(5)

故星球M的密度为

(6)

同理得星球N的密度为

(7)

因两球作为球体的半径关系为

R=3R′.

(8)

由(3)、(6)-(8)式可得ρ=ρ′

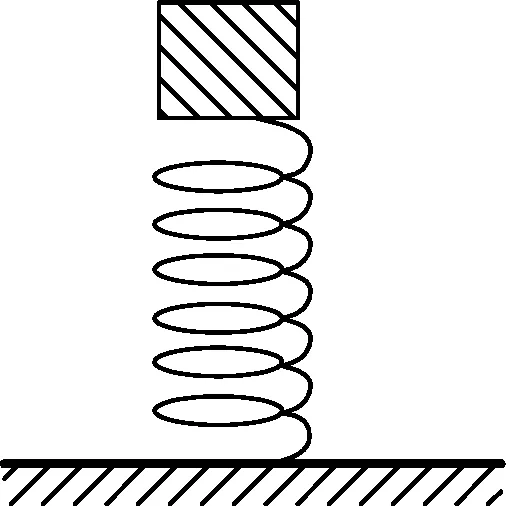
图2

2.2 两物块P、Q质量的比较

解法1: 图像横截距法

物块在弹簧上向下运动时做的是变加速直线运动,当弹簧对其弹力与其重力相等时,合力为0,加速度为0,对应着a-x图像中的横截距,此时

对P:

mPgM=kx0′.

(9)

对Q:

mQgN=k·2x0.

(10)

由(3)、(8)、(9)式得两物块质量关系为mQ=6mp;

解法2:图像斜率法

取向下为正方向,物块自静止压缩弹簧时由牛顿第二定律得

F合=mg-F弹=ma.

(11)

由胡克定律得

F弹=kx.

(12)

由图像得

对P:

(13)

对Q:

(14)

综合(12)、(13)两式有mQ=6mP.

2.3 两物块P、Q最大动能的比较

解法1:动能定理法

物块P由静止运动至合力为零时速度最大、动能最大,这一过程由动能定理得

WG+W弹=Ekmax-0

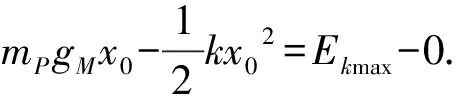
(15)

又物块P有最大动能时

kx0=mPgM.

(16)

由(14)、(15)得

(17)

同理可得在星球N上压缩弹簧的Q物块的最大动能

(18)

由(16)、(17)得

选项(C)正确．

解法2:机械能守恒法

物块P由静止运动至合力为0时速度最大、动能最大,这一过程由物块与弹簧构成的系统机械能守恒得(物块P减少的机械能转化给弹簧的弹性势能)

(19)

当然kx0=mPgM.

(20)

由(18)、(19)式得

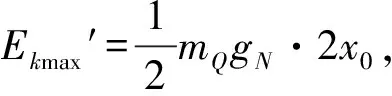
解法3:能量守恒法

物块P由静止运动至合力为0时速度最大、动能最大,这一过程由能量守恒(物块减少的重力势能转化为物块的动能和弹簧的弹性势能)得

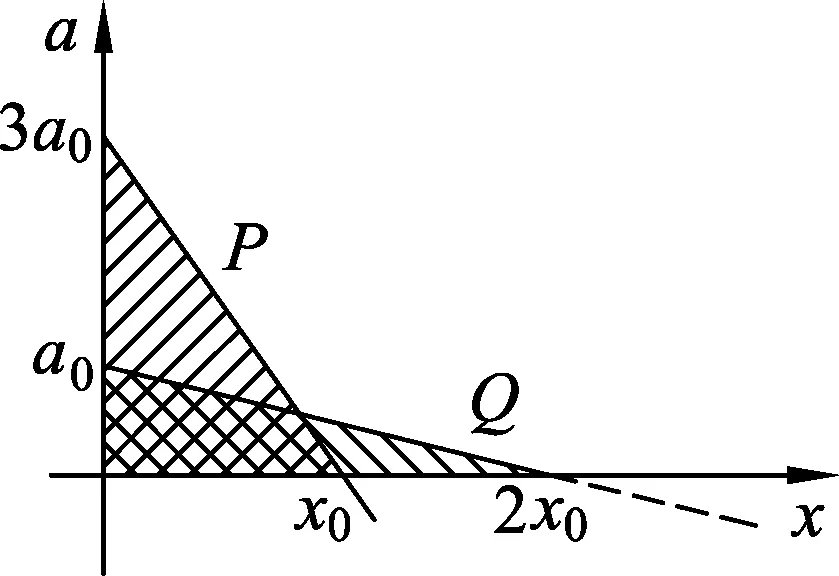
图3

解法4:a-x图像的面积法

由v-t图像的面积表示位移大小、F-x图像的面积表示功、a-t图像的面积表示速度变化量易推知a-x图像的面积表示速度平方的一半．

对P:

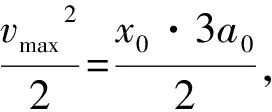
对Q有:

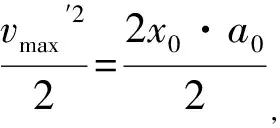
因为mQ=6mP,

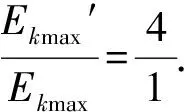
2.4 两弹簧最大压缩量的比较

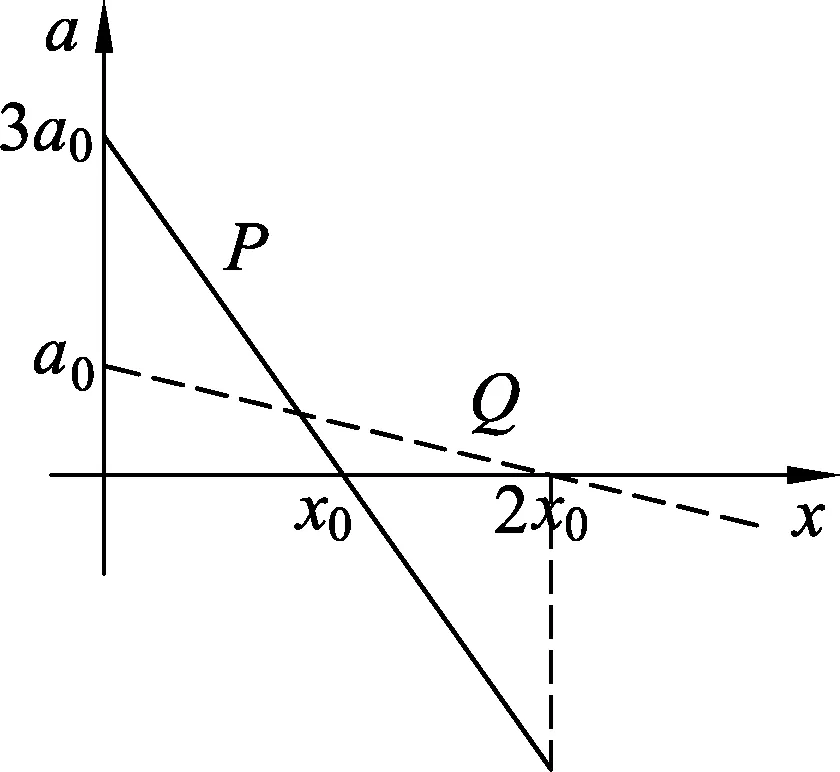
图4

由上述解法4中a-x图像面积的意义易知,物块从接触弹簧至速度最大,再从速度最大至速度为0(此时弹簧压缩最缩),这两过程应当是一对称过程,因而P所在弹簧最大压缩量为2x0、Q所在弹簧最大 压缩量为4x0,即Q所在弹簧最大压缩量为P弹簧最大压缩量的2倍．

当然也可以分别将两者的a-x延长至x轴下方面积与x轴上方面积相等处,即有此时的最大压缩量分别为2x0、4x0

3 试题导向与教学建议

3.1 要重视基础知识、基本规律的相互关联渗透

物理概念、物理定理、物理定律是构成物理学的基本元素,要想真正走进物理学、了解物理学、学习物理学甚至于将来发展物理学都离不开对基础知识、基本规律的学习理解,更不能停留在碎片化的知识当中,要关注规律之间的关联渗透,用整体的、联系的视角看待问题．教师在物理课堂教学中要有关联知识、关联规律的思想意识．

3.2 要关注利用数学方法处理物理问题的能力培养

运用数学方法处理物理问题的能力是高考物理考试纲要中明确规定的五大能力之一．图像的横纵截距、图像的斜率和面积所蕴含的意义往往是借助数学工具、利用物理规律推导出两物理量间的定量关系,通常来说,每一个物理图像背后必定有与之相对应的函数关系式,函数关系式的推导那必定要运用到数学工具,因此,对学生运用数学工具处理物理问题的能力要重点培养．

3.3 要用发展的眼光看待问题,不能墨守成规

纵观近几年全国卷Ⅰ对万有引力定律及其应用的考查,题型、分值都较为稳定,题型常为单项选择题或多项选择题,分值一直维持在6分,知识点的考查较为单一,较少出现与其他定理定律的综合考查,如2015年全国卷Ⅰ的“嫦娥三号”登月问题、2016年的同步卫星问题、2018年的双星系统问题均以万有引力定律为主要考查点,尚未与其他知识点相互渗透考查,但2019年则一反常态,将其设为选择题的压轴题,显得独树一帜,推陈出新,一改以往的命题风格,试题借助a-x图像不仅考查了万有引力定律、牛顿第二定律、胡克定律、机械能守恒定律和能量转化与守恒定律等经典的力学定律,还考查了动能定理这一重要定理．对学生理解图像、综合分析图像、结合具体情景分析图像的能力提出了相当高的要求．

因此教师在组织复习备考时千万不能随意预测,觉得每年都单独考查的某一知识点那来年一定还会是单独考查,不可能与其他知识渗透综合考查,教师千万不能有这样的思想观念,2019全国卷Ⅰ的第21题 就给我们敲响了警钟．

3.4 要培养学生一题多解的发散思维能力

在日常教学中要强调、鼓励学生一题多解和多题一解,一题多解可以锻炼学生的发散性思维,多题一解可以发展学生归纳推理的思维．以知识为载体,以能力为立意,将物理学的研究过程呈现给学生．