巧用图解法分析一类含弹簧的力学动态问题

周 勇 袁 宁

(1. 深圳实验学校高中部,广东 深圳 518055;2. 惠州市实验中学,广东 惠州 516001)

力学动态问题是高中物理中很常见的一种题型,在历年高考题和各类模拟题中常有涉及,而图解法在分析力学动态问题时往往可以回避繁琐的计算,具有方便、直观的优势,本文将结合实例介绍一种用于分析一类含弹簧(橡皮筋)的力学动态问题的图解法．

1 问题引入

图1

例1.(2014年全国卷Ⅰ)如图1所示,用橡皮筋将一小球悬挂在小车的架子上,系统处于平衡状态．现使小车从静止开始向左加速,加速度从零开始逐渐增大到某一值,然后保持此值,小球稳定地偏离竖直方向某一角度(橡皮筋在弹性限度内)．与稳定在竖直位置时相比,小球的高度

(A) 一定升高.

(B) 一定降低.

(C) 保持不变.

(D) 升高或降低由橡皮筋的劲度系数决定.

1.1 常规分析

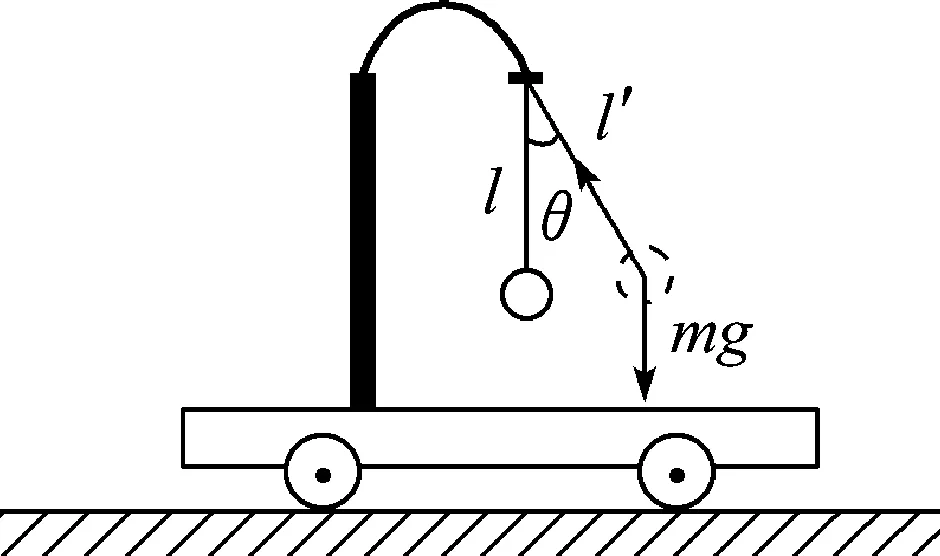
图2

设橡皮筋原长为l0、劲度系数为k,静止时,橡皮筋长度为l,加速时长度为l′且与竖直方向夹角为θ,如图所示．由胡克定律可知,静止时k(l-l0)=mg,加速时小球受力分析如图所示,由竖直方向受力平衡可知

k(l′-l0)cosθ=mg.

k(l′-l0)sinθ=ma.

则k(l-l0)=k(l′-l0)cosθ.

l′cosθ=l-l0(1-cosθ).

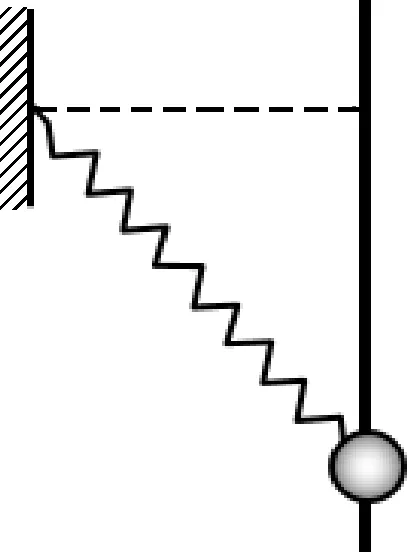
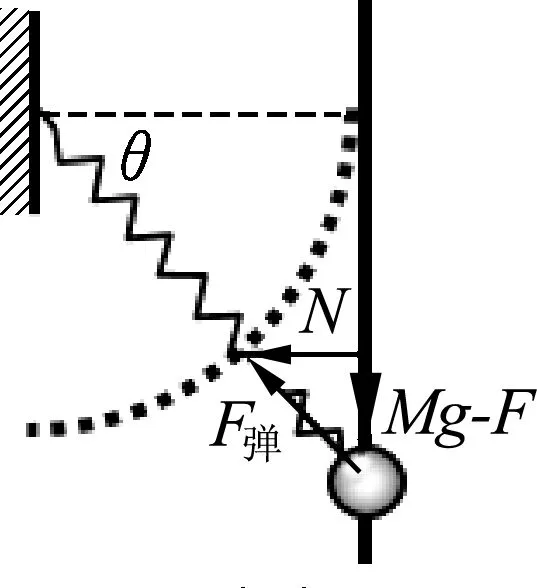
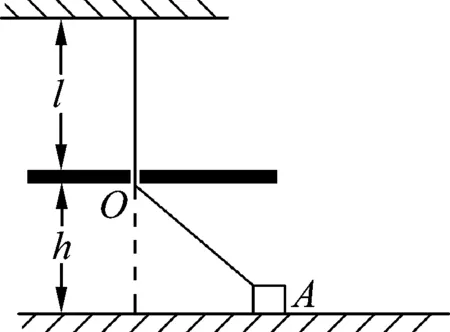
即l′cosθ

所以小球高度一定升高,故选项(A)正确．

1.2 图解法分析

图3

如图3所示,设橡皮筋原长为l0、劲度系数为k,以悬挂点为圆心,以原长l0为半径做一个圆,那么圆以外的部分长度就是橡皮筋的伸长量,设系统静止时橡皮筋的伸长量为Δl,由平衡条件可得

mg=k·Δl.

(1)

设系统加速时橡皮筋的伸长量为Δl′,此时作出小球受力的矢量三角形图并构造一个以Δl′为斜边、另两条直角边分别沿竖直和水平方向的几何直角三角形,如图3所示．显然,两个三角形具有相似关系,根据对应边成比例,可得

(2)

联立(1)、(2)可知Δh=Δl.

所以l0cosθ+Δh

1.3 方法优化

图4

考虑到这类动态问题往往都只需要作定性分析,因此,我们在分析方法上还可以作进一步的优化．在图3的基础上,如果直接以橡皮筋的劲度系数k为力的单位(比例尺),那么直接用橡皮筋的形变量(圆外部分的长度)就可以表示弹力的大小了,在此基础上作出小球静止和加速运动时受力的矢量图如图4所示,此时力的三角形与图3中的几何三角形就“重合”了,该三角形的三条边长既表示几何长度又可以反映力的大小．

由于加速时力的三角形竖直边长表示小球重力,因此跟这条边对应的几何长度也等于初始静止状态时橡皮筋的伸长量,和初状态比,小球的高度相当于沿着圆弧提升了l0(1-cosθ),即小球高度一定升高,故选项(A)正确．

与常规的解析法相比,图解法以形变量为突破口,切入点低便于掌握,计算量小方便分析,在分析这类含弹簧(橡皮筋)的力学动态问题时非常有效．下面再结合实例来谈谈该方法的应用．

2 应用举例

图5

例2.如图5所示,粗细均匀的光滑直杆竖直固定,轻弹簧一端连接于竖直墙上,另一端连接于套在杆上的小球上,小球处于静止状态．现用平行于杆向上的力F拉球,使小球沿杆缓慢向上移动,当弹簧水平时恰好处于原长,则从小球开始向上运动直到弹簧水平的过程中,下列说法正确的是

(A) 拉力F越来越大.

(B) 拉力F先减小后增大.

(C) 杆对球的作用力一直减小.

(D) 杆对球的作用力先增大后减小.

图6

解析： 因拉力F和小球的重力都在竖直方向,可先将重力Mg与F合成,等效为一个力(Mg-F)．以弹簧原长为半径作一个圆,以弹簧的劲度系数k为力的单位,那么弹簧在圆外部分的长度就可以表示弹簧弹力大小了,在此基础上作出小球静止时受力的矢量图,如图6所示．当小球缓慢向上移动时,显然,杆对球的作用力N一直减小．设弹簧与水平方向的夹角为θ,由矢量图可得

Mg-F=F弹sinθ.

解得F=Mg-F弹sinθ.

当小球缓慢向上移动时,弹簧弹力F弹减小,θ减小,从而拉力F增大,故选项(A)、(C)正确．

图7

(A) 移动后滑块对地面的压力变小.

(B) 移动后滑块对地面的压力不变.

(C) 移动后滑块将加速运动.

(D) 移动后滑块仍能静止.

图8

解析: 因地面的支持力N和滑块所受的重力G都在竖直方向,可先将小球的重力G与支持力N合成,等效为一个力(G-N)．因弹性细绳的原长l与小孔O离绳固定端的竖直距离相等,若以劲度系数k为力的单位,那么OA部分的长度就可以表示弹性绳的弹力F大小了,在此基础上作出滑块静止时受力的矢量图,如图8(实线)所示．若把滑块向左移动少许,假设滑块仍能静止,此时其受力矢量图如图中虚线所示．显然,重力G与支持力N合力不变,从而可知移动后滑块对地面的压力不变;若移动后滑块仍能静止,那么地面的摩擦力减小,小于初状态所受摩擦力,也就小于最大静摩擦力,说明移动后滑块确实静止,故选项(B)、(D)正确．

3 结束语

本文介绍的这种图解法从相似三角形法演变而来,关键思想包括以下两个方面: (1) 借助辅助圆或辅助线段将弹簧(弹性绳)的原长截去,于是可以通过圆外的部分长度直观的反映弹簧的伸长量及其变化;(2) 以劲度系数k为力的单位(比例尺),弹簧的伸长量就可以直接表示弹力大小．在此基础上,再作出物体受力的矢量图,结合相关长度和角度的变化就可以很方便的看出某些力的变化,可以有效的避免繁琐的数学计算,快速得出结果．