从相位传播的角度计算多普勒频移的“降阶”方法
——对一道全国中学生物理竞赛复赛试题解答的思考
郑金山
(莆田第四中学,福建 莆田 351100)
第32届全国中学生物理竞赛复赛试题第4题,设置了机载测地雷达的电磁波多普勒频移的讨论. 其中第1问的原参考解法,从电磁波中的相位传播的角度进行计算. 由于采用了解析几何的框架,演算比较复杂. 根据其思路,在给高中生讲解时,借鉴《力学》[1]教材中的处理,尝试通过结合信号传播路径的几何关系,计算信号传播时间,分析多普勒频移,降低了计算的难度.
1 原题及解答思路
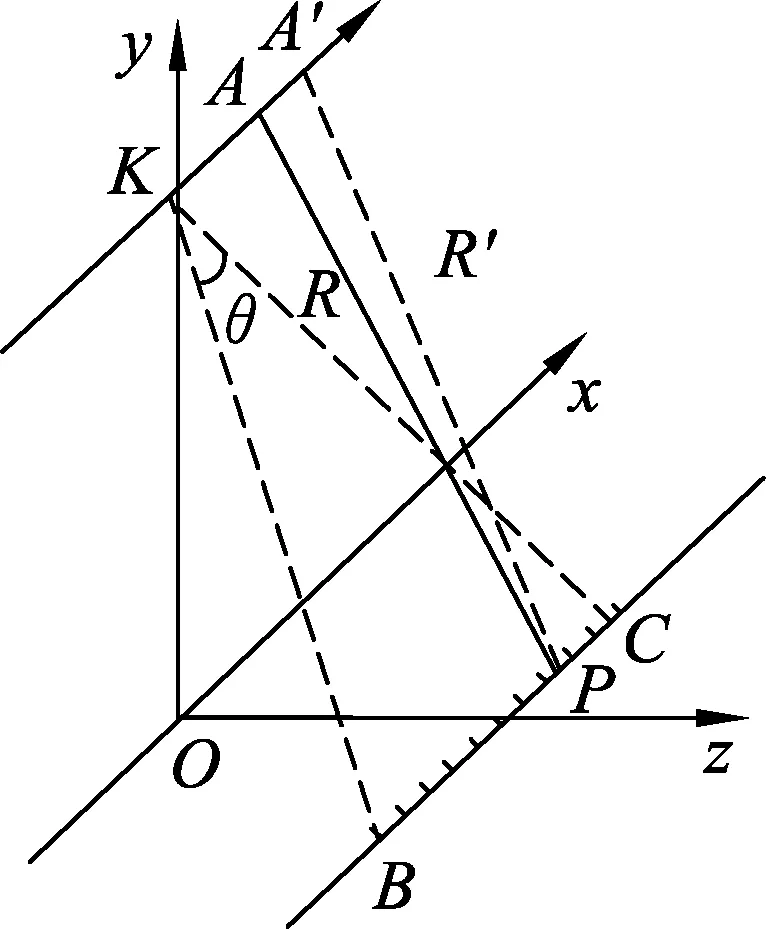
图1
(32届全国中学生物理竞赛复赛第4题1问)[2]如图1,飞机在距水平地面(xz平面)等高的航线KA(沿x正方向)上,以大小为v(v远小于真空中的光速c)的速度匀速飞行;机载雷达天线持续向航线正右侧地面上的被测固定目标P点(其x坐标为xP)发射扇形无线电波束(扇形的角平分线与航线垂直),波束平面与水平地面交于线段BC(BC随着飞机移动,且在测量时应覆盖被测目标P点),取K点在地面的正投影O为坐标原点. 已知BC与航线KA的距离为R0. 天线发出的无线电波束是周期性的等幅高频脉冲余弦波,其频率为f0. 已知机载雷达天线经过A点(其x坐标为xA)及此后朝P点相继发出无线电波信号,由P反射后又被机载雷达天线接收到,求接收到的回波信号的频率与发出信号的频率之差(频移).

原解答过程[2]对数学运算能力的要求比较高,为了便于直观理解,笔者尝试从两个信号(余弦电磁波脉冲)的传播路径的几何关系入手,分析两个时间间隔的关系. 由于采用几何的方法,比较直观,高中生更为熟悉,可以降低学习难度.
2 从几何直观上分析,考虑信号传播过程进行求解

图2
如图2所示,先把三维的空间描述,转换为二维平面上的情形.当飞机飞到A点,从波源发出一个波峰(仅为了便于理解,当然可以是某个其它的相位)开始计时,这个波峰相位向空间传播,遇到目标P发射回来,接收器接收到了这个波峰的回波信号. 在波的传播过程中,实际上飞机载着雷达以飞行速度沿航线运动. 这时飞机已经飞到了A′点.在发出第1个波峰之后,过了1个周期(源周期)τ的时间,当飞机飞到B点时,下一个波峰信号(或者延后了2π的相位)从雷达出发,向空间传播,同样被目标P反射后,接收器接收到了它的回波信号. 此时飞机飞到了B′点. 接收器接收到的两个信号的时间间隔,即为接收到的信号的周期τ′. 如果能够得到发射周期(源周期)和接收周期的关系,就可以计算出接收到的频率.
假定在t1时刻,第1个波峰从A出发,到达P反射回来,到点A′被接收. 设所用的时间为t,有
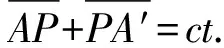
(1)
信号到达A′的时刻为
(2)
当飞机飞到B处时,发出下一个波峰信号,此时刻为t2=t1+τ,此信号传播出去,遇到P反射回来,到B′点被接收. 设所用的时间为t′,有

(3)
信号到达B′的时刻为
(4)
相邻两个波峰到达接收机的时间间隔
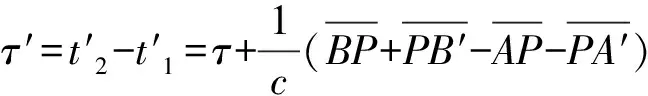
(5)
需要借助辅助线讨论,从B′作B′D⊥A′P于D,从B作BE⊥AP于E.


(6)


(7)
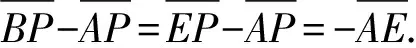
(8)
在直角三角形ΔA′DB′中,
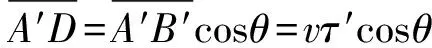
(9)
式(9)中θ=∠B′A′D.
在直角三角形ΔAEB中,

(10)
式(10)中φ=∠BAE.
由几何关系∠B′A′D=∠BAE+∠A′PA,令δ=∠A′PA,则有θ=φ+δ. 讨论式(9)和式(10)中两个角的余弦,有
cosθ=cos(φ+δ)=cosφcosδ-sinφsinδ,
(11)
由(6)可知,δ是一个小角度,δ≪1,cosδ≈1,sinδ≈δ,由式(11)得
cosθ=cosφ-δsinφ.
(12)
代入式(9),有

(13)
由式(6),vτ′是长度的一阶小量,δ是弧度一阶小量,sinφ是一个随飞机飞行位置变化的有限数值,所以(vτ′)δsinφ是一个长度的二阶小量,可以忽略. 式(13)可以变形为

(14)
将式(7)、(8)、(10)、(14)代入(5)可得

(15)

(16)


(17)
(18)
这里,飞机飞行的航线和从飞机射向目标P的光线的夹角为φ,飞机还未飞到F,此时飞机和目标之间是靠近的趋势,cosφ>0,Δf=f′-f0>0,f′>f0,表现为频率变大的现象;若飞机飞到F点,cosφ=0,没有频率差;若飞机飞过了F,cosφ<0,飞机和目标之间是远离的趋势,表现为接收到的频率比源频率减小的现象. 这和教材[3]中的讨论是一致的. 从图2中可以看出,产生信号周期差的原因是由于信号回程时少走了一段路程,导致接收到的信号周期比源周期小.
3 进一步的思考
以上通过分析两个相隔一个周期(相位相差2π)的波峰信号的传播过程,求解出多普勒效应中的接收到的信号周期和源信号周期的关系,从而求出频率差.这种方法同样适用于教材[3]中的几种情况的讨论: (1) 波源相对观察者运动,观察者静止; (2) 波源静止,观察者相对波源运动; (3) 超声波雷达测速,雷达不动,目标相对雷达运动. 这些情境中的频移讨论,也可以从相位传播的角度,应用几何路径分析的方法进行计算.
4 对解答的反思
原题解在坐标系中严谨的进行了代数解析,运算要求较高,可以作为更高的要求去学习掌握,具有更广阔的应用前景,例如这样可以更方便的编制程序进行数值计算等. 本文的讨论可以作为一个过渡,为学生理解原解答打下基础. 另外在处理几何的关系过程中,需要正确判断高阶小量并略去,突出主要因素,这是竞赛解题中的运算的一项基本要求.
5 总结
基于相位传播的计算多普勒频移方法,可以解决一般的多普勒频移的计算问题. 教师采用几何方法帮助学生分析信号传播路径,计算信号相位传播的时延,可以帮助降低计算难度,达到数学技巧“降阶”,而物理直观“升阶”的目的,提高竞赛辅导的实效.

