中空孔对直眼掏槽爆破效果的影响数值模拟

罗剑辉，程 兵，汪海波，宗 琦

（安徽理工大学 土木建筑学院，安徽 淮南 232001）

掏槽爆破是决定隧道或巷道掘进爆破中整体破岩效果及循环进尺大小的关键所在[1]。合理的掏槽方法有利于岩体爆破成腔，为后续爆破提供较大自由面，以达到良好爆破效果。基于掏槽孔与临空面的空间位置关系进行区分，可将掏槽分为直眼掏槽和斜眼掏槽[2]。直眼掏槽凭借其具有炮孔不受断面大小限制、可以多台机械同时钻孔、能实现较高的炮眼利用率、爆堆集中等特点，成为隧道或井巷爆破开挖中常用的掏槽方法，因此研究中空孔对直眼掏槽爆破效果影响具有重要的工程实际意义。

林大能等[3]基于力学理论分析了直眼掏槽时掏槽孔装药爆破形成空腔的整个历程以及腔内岩体的抛掷飞散行为，同时构建了空腔演变过程的理论模型以及空腔尺寸的求算方法。刘优平等[4]从理论上分析了中空孔直眼掏槽爆破机制，并对中空孔的作用进行进一步阐述，认为：随着中空孔直径的增加应力集中效应会更加显著，并通过现场试验证明使用大直径中空孔是取得良好掏槽效果的必要方法。李启月等[5]采用显式动力分析软件对掏槽孔与不同直径中空孔间的裂隙贯穿历程进行了数值模拟，结果显示：随着中空孔直径增加，岩体破坏过程中的拉、压破坏特征则愈加显著。张祖远等[6]基于现场工程实际研究了采用中空孔直眼掏槽时，掏槽孔数量、中空孔直径、掏槽孔与中空孔距离、微差起爆间隔时间等不同参数条件下爆破振动的变化规律。左进京等[7]通过模型实验研究了不同直径中空孔掏槽腔体的爆破破坏形式，并利用高速摄像获得了不同中空孔直径下槽腔岩体向外抛掷的过程，阐述了不同直径中空孔直眼掏槽的内在差异。

现有研究较少利用数值模拟手段研究中空孔直眼掏槽的应力场分布及掏槽爆破效果。鉴于此，拟运用ANSYS/LS-DYNA，建立有、无中空孔2 种直眼掏槽爆破的三维数值模型，比较分析掏槽爆破过程中爆炸应力场演化历程以及岩体破坏特征。

1 数值模拟

1.1 建立数值模型

运用ANSYS/LS-DYNA 建立2 组有、无中空孔的三维直眼掏槽爆破模型，且为了减少计算量和求解时间，基于模型自身的对称性可以将模型简化为1/2 模型。数值计算模型如图1。

图1 数值计算模型Fig.1 Numerical calculation model

有中空孔模型：模型中间设置中空孔，中空孔深度为2 700 mm，直径为100 mm。中空孔的四周按菱形布置4 个掏槽孔，中空孔与掏槽孔距离为300 mm，掏槽孔深度为2 500 mm，直径为42 mm，采用不耦合装药结构，炮孔内装填直径为35 mm 药卷，装药长度为1 200 mm，炮泥填塞长度为1 300 mm。无中空孔模型除没有中空孔存在以外，其他炮孔参数和装药参数等均与有中空孔模型相同。

研究中岩体和炮泥采用Lagrange 网格，炸药和空气采用Ale 网格，炸药和空气与岩体和炮泥之间的交互作用通过罚函数耦合算法进行定义[8]。模型外侧除孔口端为临空面外均需要设置无反射边界，用于吸收剪切波和膨胀波以降低边界应力波反射对结果的干扰，从而更接近岩体在无限介质中的实际受力状态[9]。2 组模型均采用由孔底向上传爆的反向起爆方式，通过*INITIAL_DETONATION 关键字在掏槽孔底部定义起爆点。

此外，由于炮孔近区应力场较为复杂，需将炮孔近区网格进行细化，远离炮孔区域的网格相对稀疏，在确保计算精度的同时能够保障求解效率。

1.2 材料模型及参数

炸药采用 *MAT_HIGH_EXPLOSIVE_BURN 材料模型[10]，同时使用经典JWL 状态方程来描述爆炸过程中产物的体积、压力以及能量特性，式（1）表示JWL 状态方程决定的爆轰压力：

式中：peos为JWL 状态方程决定的爆轰压力，Pa；A、B 为材料常数，Pa；R1、R2、ω 为炸药材料常数，无量纲；E0为初始内能，Pa；V 为相对体积，无量纲。

炸药材料及JWL 状态方程参数见表1。

表1 炸药材料及状态方程参数Table 1 Material and equation state parameter of explosive

空气采用*MAT_NULL 空白材料模型，并同时使用LINEAR_POLYNOMIAL 线性多项式描述其状态方程[11]：

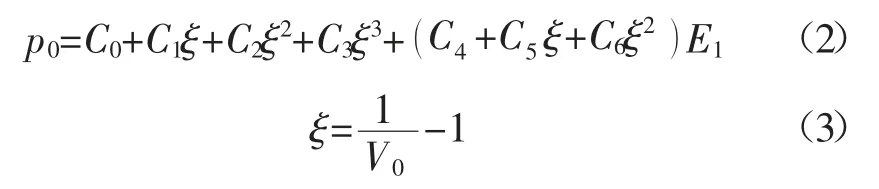
式中：p0为压强，Pa；C0、C1、C2、C3、C4、C5、C6为状态方程参数，无量纲；ξ 为黏滞系数，无量纲；E1为单位体积内能，Pa；V0为初始相对体积，无量纲。

空气材料及状态方程参数见表2。

岩体采用*MAT_PLASTIC_KINEMATIC 随动塑性强化模型，在爆炸载荷作用下岩体在极短时间内发生屈服破坏，与静载荷作用情况下相比应变率大幅度提高，岩体的力学性质发生显著改变[12]。该模型在岩体屈服应力中引入了应变率放大因子，改进后的屈服应力为[13]：

表2 空气材料及状态方程参数Table 2 Material and equation state parameters of air

式中：σY为屈服应力，Pa；λ 为放大因子，无量纲；σ0为初始屈服应力，Pa；β 为随动强化和等向强化之间的调节参数，无量纲；Ep为塑性强化模量，Pa；为等效塑性应变，无量纲；ε 为应变率，s-1；C、P 为Cowper-Symonds 应变率参数，无量纲。

岩体材料参数见表3。

表3 岩体材料参数Table 3 Material parameters of rock

炮泥采用*MAT_SOIL_AND_FORM 泡沫材料模型[14]，该模型能够较好地处理泥土等工程材料在爆炸载荷下大变形的动力响应问题。炮泥材料参数见表4。

表4 炮泥材料参数Table 4 Material parameters of stem

2 模拟结果分析

2.1 爆炸应力场分布特征

为了研究中空孔对直眼掏槽爆炸应力场的影响，基于后处理程序，得到有中空孔和无中空孔2 组模型在不同时刻的等效应力云图（图2 和图3）。

根据图2 和图3 可以看出，掏槽孔内炸药从底部开始起爆并逐渐向上传爆，爆炸应力波以柱面波的形式向外传播，当应力波传播到中空孔，在充当自由面的中空孔处发生应力波反射，中空孔附近岩体中的有效应力强度明显大于无中空孔模型，即中空孔周围产生了明显的应力集中效应。

图2 有中空孔模型不同时刻等效应力云图Fig.2 Von Mises stress isolines distribution of hollow hole model at different time

图3 无中空孔模型不同时刻等效应力云图Fig.3 Von Mises stress isolines distribution of non-hollow hole model at different time

为了能够更加直观地描述中空孔周围爆炸应力场分布特征，在2 组模型正中间上方距离掏槽孔底部600 mm 的地方各取1 个测点，通过后处理程序每隔0.02 ms 输出该测点的等效应力值，得到的2组模型测点的等效应力时程曲线如图4。

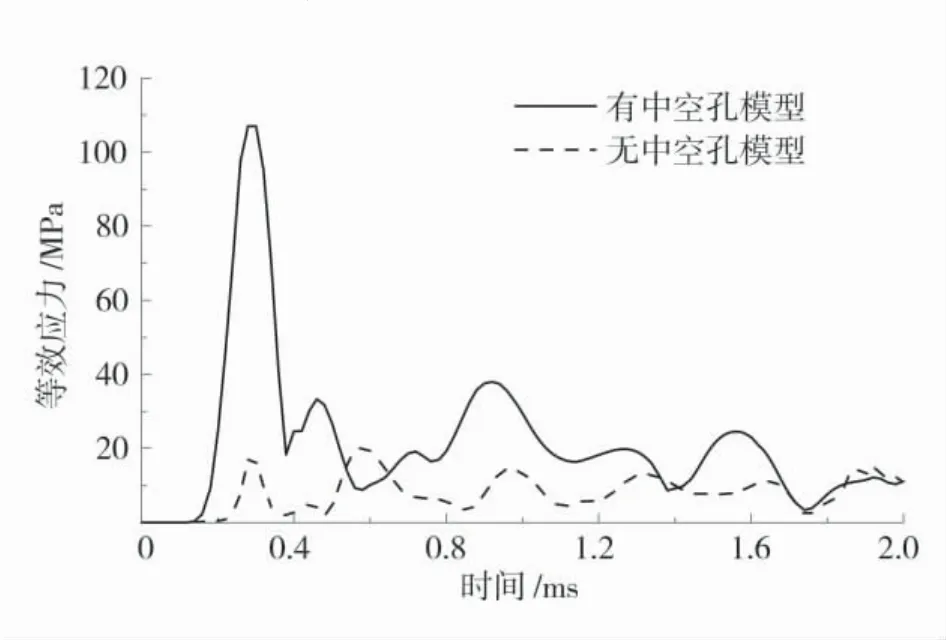
图4 等效应力时程曲线Fig.4 Equivalent stress time history curves

根据图4 可以看出，有中空孔模型孔壁测点的等效应力峰值为107.0 MPa，而无中空孔模型中心区域测点的等效应力峰值为20.3 MPa，且在2 ms内有中空孔模型孔壁测点的等效应力值基本高于无中空孔模型中心区域测点，充分说明中空孔附近产生了明显的应力集中效应。

2.2 槽腔岩体破坏情况

为了能够进一步研究槽腔岩体破坏情况，通过在k 文件中添加*MAT_ADD_EROSION 单元失效关键字，将岩体的拉、压强度参数定义为单元失效阀值，从而实现槽腔内岩体的损伤与破坏[15]。当槽腔岩体破坏演化完成以后，在上方距离掏槽孔底部600 mm 的地方垂直于炮孔方向截取横向平面，可以得到2 组模型在该处的岩体破坏情况（图5）。

图5 直眼掏槽槽腔岩体破坏情况Fig.5 Failure of rock mass in straight cut cavity

根据图5 可以看出，对于有中空孔的直眼掏槽爆破模型，槽腔内岩体能够被充分破坏，中空孔与掏槽孔之间形成了贯穿裂隙，且中空孔孔壁处发生了片状层裂，因此在爆生气体作用下该部分将会被抛掷出槽腔，形成有效的自由面；而对于无中空孔爆破模型，槽腔中间岩体保持了较好的完整性，未能够被充分破坏，在工程中的表现就是残孔、炮孔利用率低。

分析认为造成这种差异的原因在于，中空孔的应力集中导致裂纹优先向掏槽孔与中空孔的连线方向发展；应力波传播到中空孔孔壁，在中空孔孔壁上产生反射而形成拉伸应力波，由于岩石动抗拉强度较低，造成了中空孔孔壁岩体发生层裂现象。

3 结 论

1）由于中空孔处发生了应力波反射，中空孔附近产生明显的应力集中效应，中空孔模型孔壁测点的等效应力峰值为107.0 MPa；而无中空孔模型中心区域测点的等效应力峰值为20.3 MPa。

2）比较2 组模型的槽腔岩体破坏情况，有中空孔时槽腔内岩体被充分破坏，中空孔与掏槽孔之间形成贯穿裂隙，且中空孔孔壁附近形成了层裂现象；无中空孔时槽腔内岩体保持了较好的完整性。