大流速地下水作用下多圈冻结孔优化布置方法研究

董艳宾，荣传新，王 彬，杨 凡

（安徽理工大学 土木建筑学院，安徽 淮南 232001）

人工地层冻结法目前是富水软土层竖井掘砌施工的主要工法，该工法在拟施工的竖井井筒周围设置1 圈或多圈冻结管，通过冻结管中的低温冷媒与被冻土体之间不断进行热量交换，形成1 道具有一定强度、且具有良好封水性能的冻结壁，从而为井壁的掘砌施工提供1 个稳定的施工环境[1-2]。但随着施工穿越岩土层中地下水流速的增大，采用传统的冻结管布置方案时，出现了冻结壁交圈时间增加甚至无法交圈的问题，这导致后期的土体开挖以及井筒的施工无法如期开展，造成了巨大的经济损失。因此，对大流速地下水作用下的人工立井冻结温度场的形成规律展开研究具有重要的工程意义[3-5]。

在试验研究方面，周晓敏等[6]通过双管冻结正交模型试验，研究了常规盐水（温度为-26.0～-30.6℃）冻结工艺中，地下水渗流、孔间距等对饱和砂冻结交圈时间和上下游温度场发展规律的影响。Huang R C[7]进行了渗流条件下的单一冻结管的模型试验，发现地下水流会导致冻结管上、下游的冻结面积与无渗流条件相比出现了不同程度的减小。Li Yan Lao[8]通过模型试验得出了不同流速的地下水作用下，单排三管冻结温度场的发展规律。王朝晖等[9]对液氮（-80 ℃）冻结条件下地下水流速对冻结温度场的影响开展了研究，其结果表明10 m/d 以上的动水对液氮冻结效果有显著的影响。Vitel M[10]等设计了1 种与热力学原理完全一致的水热耦合数学模型，用于模拟渗流条件下饱和不可变形的多孔介质的人工地层冻结，完成了高渗流速度条件下三维冻结试验，为多孔介质相变相关的水热耦合研究提供了关键参数依据。Pimentel E 等[11]总结了之前学者的研究成果，并考虑到冻结冷量散失等问题，重新设计了试验装置，分别进行了流速为0、1、1.5、2.0、2.1 m/d 的渗流条件下人工地面冻结的大型模型试验，根据试验结果从冻结柱状体的交圈时间与所需冷量的角度出发，对冻结壁的交圈形式解进行了讨论，为冻结法的数值计算以及工程应用提供了重要依据。

由于大型相似模型试验的限制因素较多，且只能部分还原冻结温度场的发展规律，而数值计算则可以解决这一问题，因此数值计算一直是研究水热耦合问题的重要技术手段。在数值计算研究方面，杨平等[12]利用多孔介质热运移理论及达西定律，建立了考虑地下水流作用的单根冻结管冻结峰面发展的数学模型，分析了冻结过程中温度场及地下水流场的变化规律。高娟[13]以及刘建刚等[14]分别运用有限元的方法对地下水作用下竖井和水平冻结的温度场形成规律进行了研究。Vitel M[10,15-16]为了模拟在渗流条件下饱和不可变形多孔介质的人工地面冻结过程，构建了与热力学一致的水热数值模型，并对通常使用的限制性假设进行了简化，该模型在高渗流速度条件下的三维地面冻结实验中得到了很好的验证。黄诗冰等[17-19]通过考虑水/冰相变，开发了水热耦合模型来模拟水流对冻结过程的影响，并将该模型与基于COMSOL 多物理场平台的Nelder-Mead 单纯形法相结合，优化了圆形隧道周围冻结管的位置。Ahmed 等[20]结合“蚁群算法”对小流速地下水作用下冻结管的布置位置进行了优化设计，从而加快了冻结壁的交圈并使形成的冻结壁的强度更加均匀，为冻结方案的优化设计开拓新的思路。

将在上述研究的基础上，通过对比单管水热耦合模型与试验结果，验证水热耦合模型的正确性和相关参数取值的合理性。根据验证的水热耦合模型，采用对淮南矿区潘一煤矿副井冻结法施工的上游外圈冻结管进行局部加密的方法，来实现对常规冻结方案的优化设计，并通过COMSOL 有限元软件对优化效果进行研究。

1 渗流场和温度场的耦合模型的建立

1.1 基本假设

在冻结过程中，土体是由土体骨架、水、空气以及冰构成的多相体系。假设冻结过程中的土体保持为1 种饱和状态。考虑研究的重点及主要影响因素，在计算模型过程中做出如下假定：

1）忽略冻结管周边的热量损失，即视冻结管内、外壁的温度相同，且都等同于低温冷媒温度。

2）流体作为连续介质充满渗流区的全部空间，初始状态为稳态渗流且符合达西定律，不考虑冻结过程中的质量迁移。

3）冻结土层为连续的、均匀的、各向同性的多孔介质，满足混合物理论的基本假定。

4）在冻结过程中仅考虑土体基质、水、冰的热传导效应及冰、水在相变温度区域范围内发生，且未冻水含量仅与温度有关。

1.2 水热耦合控制方程

冻结过程的温度变化属于瞬态热传导问题，根据基本假定，则在冻结过程中，土体中同时存在冰、水和土体骨架，且三者存在不同的传热特征：除了传导传热以外，冰的热量传递还包括相变传热；水的热量传递还包括液态水流动产生的对流传热。根据传热及渗流原理，冻结过程考虑相变的温度场与渗流场控制方程为[5,15]：

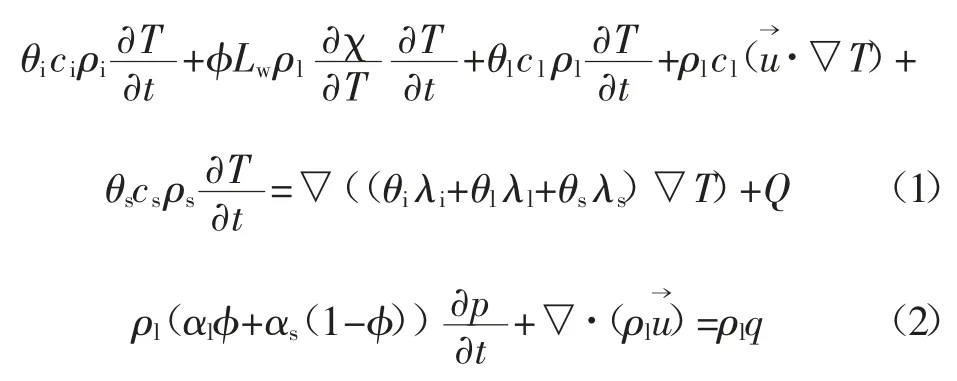
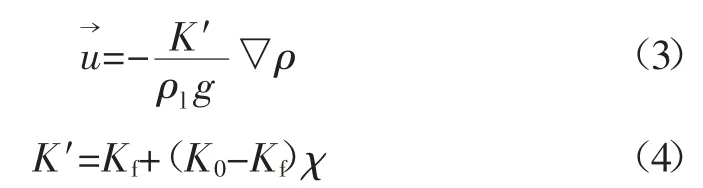
式中：t 为时间；T 为控制体温度；χ 为空隙中未冻水体积含量；ci、cl、cs为冰、水、土骨架的比热容；λi、λl、λs分别为冰、水、土骨架的导热系数；ρi、ρl、ρs为冰、水、土骨架的密度；Lw为单位质量水的相变潜热值为水的相对速度矢量；Q 为等效热源强度；αl为水的压缩率；αs为控制体等效压缩率；φ 为孔隙率；p 为渗透压力；q 为流量；K′为等效渗透系数；Kf、K0为完全冻结区和未冻区的渗透系数；θi、θl、θs为控制体的含冰率、含水率、土骨架含量；g 为重力加速度。

2 水热耦合模型的验证

2.1 物理模型试验的设计

为验证水热耦合数学模型的合理性，采用相似模型试验进行验证。为了减小因模型尺寸缩小而带来的失真影响，并考虑试验室条件的基础上，取几何相似比为C1=3，根据相似准则，测点布置如图1。

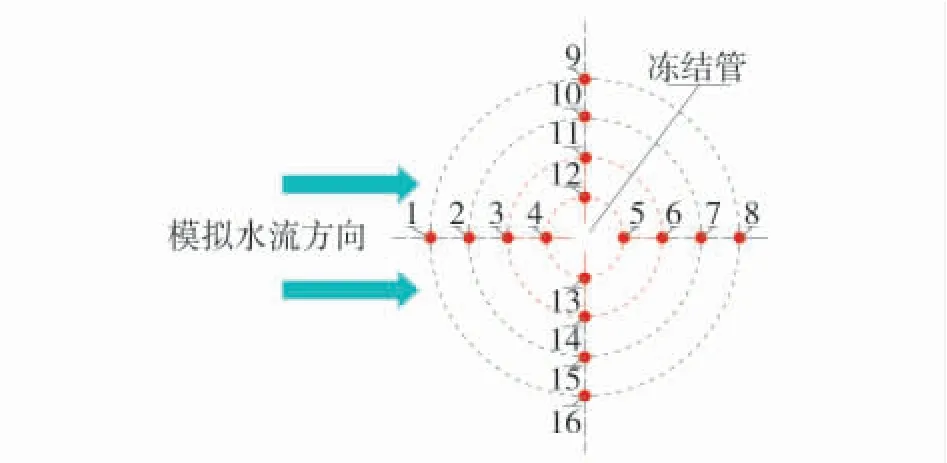
图1 测点布置方案Fig.1 Measuring point arrangement

试验选用粒径为1 mm 的圆粒砂来模拟多孔介质，砂的物理参数和热参数见表1 和表2。

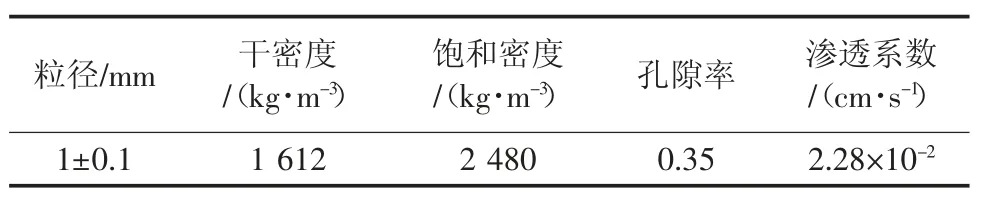
表1 砂子物理参数Table 1 Physical parameters of the sand

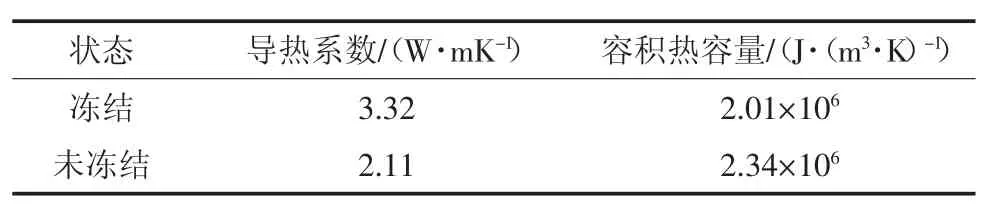
表2 砂子热参数Table 2 Thermal parameters of sand

为了防止外界的环境温度对冻结过程产生干扰，对箱体外表面以及冻结管路进行了保温处理：紧贴箱体外表面布置1 层30 mm 的橡塑保温板，随后采用40 mm 的聚氨酯保温板将整个箱体包裹在其中，接缝处用氯丁胶紧密粘合，外露的冻结管以及冻结干管表面包裹1 层30 mm 的橡塑保温层。保温层的布置情况如图2。

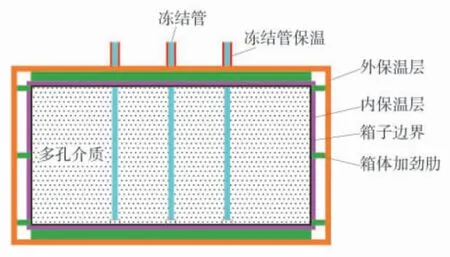
图2 箱体表面保温层设置情况Fig.2 Insulation layer setting of case surface

2.2 试验方法及测试方案

1）进行基础试验，测定选用的砂层的导热系数、质量比热、孔隙率、渗透率。

2）试验设备安装与调试，标定变频泵、压力表、流量计及测温系统。

3）设置变频泵的恒压数值改变水箱内水压，调节进水流量控制阀改变清水流量，控制通过砂层的清水流量，使砂层中渗流水速度达到设计值，由PLC控制变频泵，保证试验过程中上下游压力差恒定。

4）调节酒精温度至-32 ℃，开启酒精泵，通过调节酒精流量来使酒精供冷量达到设计值，记录开泵时间。

5）开启记录数据，间隔5 min 记录箱体边界温度、砂层温度、进出清水温度、去回路酒精温度和环境温度。

2.3 数值计算结果与模型试验结果对比

依据COMSOL Multi-physics 中的场方程，利用Porous Media and Subsurface Flow 模 块 和 Hear Transfer in Porous Media 模块的瞬态分析功能，将各个参变量代入方程，并调用借助Matlab 编制的内插函数与耦合方程，实现了冻结过程中水热耦合数学模型的瞬态求解。将1#～8#测点在流速分别为0 m/d和2 m/d 时的数值计算结果与模型试验结果进行对比，两者温度随时间和位置变化对比结果如图3，两者的量化比较见表3。

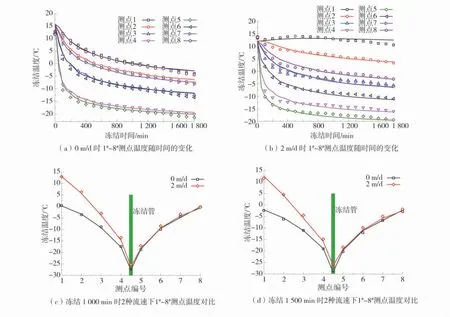
图3 温度变化规律对比分析Fig.3 Comparative analysis of temperature change law

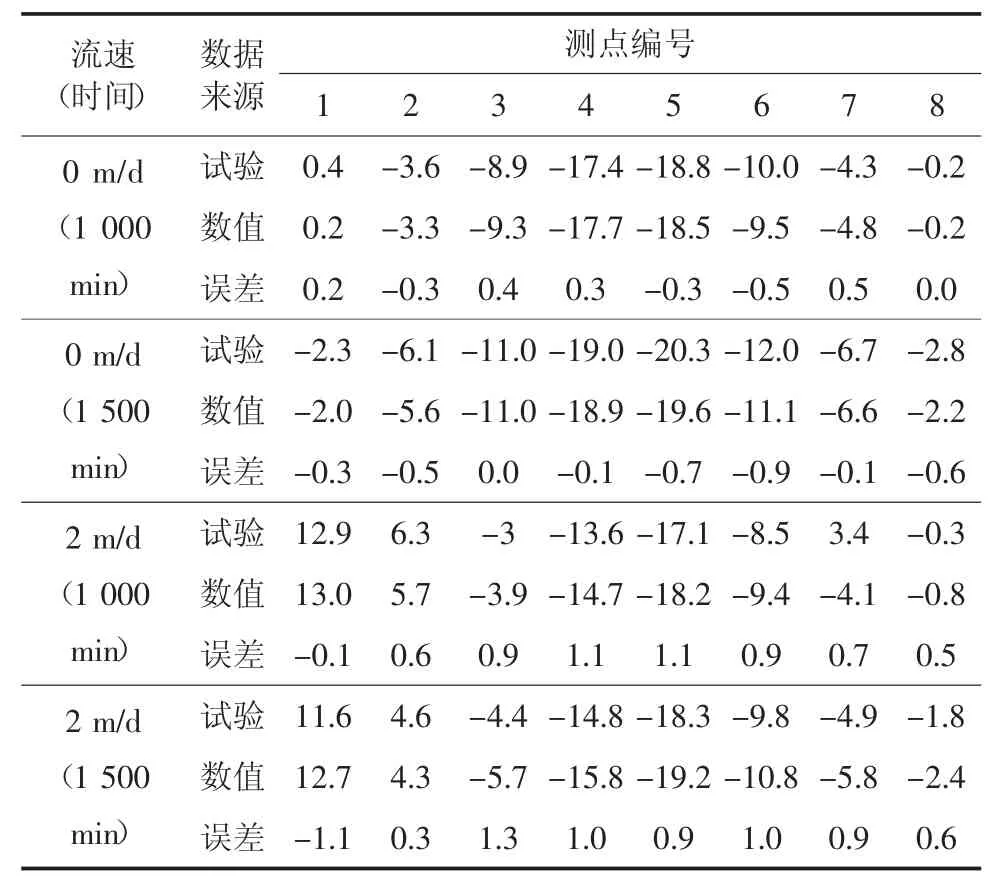
表3 数值计算结果与试验结果比较Table 3 Comparison between numerical calculation results and test results

1）由图3（a）和图3（b）可知，数值计算结果与模型试验结果基本一致。流速为0 m/d 时，1#～8#测点均经历了快速降温阶段和稳定降温阶段；流速为2 m/d 时，上游距离冻结管较远的1#、2#测点仅有稳定降温阶段，而较近的 3#、4#测点和下游 5#、6#、7#、8#测点则都经历有快速降温阶段和稳定降温阶段。

2）由图3（c）和图3（d）可知，在流速为 0 m/d 冻结1 500 min 时，对称点测点1#与8#的温差为0.2℃、2#与 7#的温差为 1.0 ℃、3#与 6#的温差为 0.1℃、4#与5#的温差为0.7 ℃，对称测点的温差绝对值均不大于1.0 ℃，可知测点的温度变化具有位置对称性；流速为2 m/d 冻结1 500 min 时，对称点测点1#与 8#的温差为 15.1 ℃、2#与 7#的温差为 10.1 ℃、3#与 6#的温差为 5.1 ℃、4#与 5#的温差为 3.4 ℃。这是因为在地下水流的作用下，冻结管上游的一部分冷量会被水流带到下游，使得上游测点降温慢，下游测点降温快；由于水流会抑制冻结管冷量向上游传递、并促进向下游传递，随着距离冻结管距离增加，这种抑制和促进作用越明显。因此关于冻结管对称的下游测点温度低于上游测点，且测点距离冻结管越近，两点的温度差值越小。

3）由表3 可知，1#～8#测点在冻结 1 000、1 500 min 时，地下水流速分别为 0、2 m/d 时，0 m/d 的数值计算的平均误差分别为 0 ℃和-0.4 ℃、2 m/d 的数值计算的平均误差为 0.7 ℃和 0.6 ℃，均小于 1.0℃；且仅有个别测点在某些时刻的误差绝对值超过1 ℃，因此判定数值计算结果与试验结果的整体吻合度较高，而个别测点在某些时刻的误差绝对值超过1 ℃，可能是由于试验测量误差导致的。

3 工程应用

3.1 参数与优化方案

淮南矿区潘一煤矿副井冻结法施工的设计参数如下：①井筒净直径：7.500 m；②拟开挖直径：8.000 m；③内圈管冻结管布置圈径：14.00 m；④内圈管数量：27；⑤内圈管管间距：1.625 m；⑥内圈管冻结管壁温度：-32 ℃；⑦内圈管冻结管尺寸：φ0.140 m；⑧外圈管冻结管布置圈径：18.00 m；⑨外圈管数量：43；⑩外圈管冻结管间距：1.314 m；1○外圈管冻结管壁温度：-32 ℃；12○外圈管冻结管尺寸：φ0.140 m；13○排间距：2.000 m。其中 200 m 层位处为粉质砂层，该层位地下水流速较大，在按照原设计方案进行冻结法施工过程中，发现冻结壁发展速度较慢。

对原冻结方案进行优化，优化参数如下：①优化冻结管布置圈径：18.00 m；②优化冻结管加密角度：120°；③优化冻结管增加数量：4 根；④优化冻结管间距：1.006 m；⑤优化冻结管壁温度：-32 ℃；⑥优化冻结管尺寸：φ0.140 m。优化前后冻结管的布置方式如图4。优化前后的数值计算模型如图5。

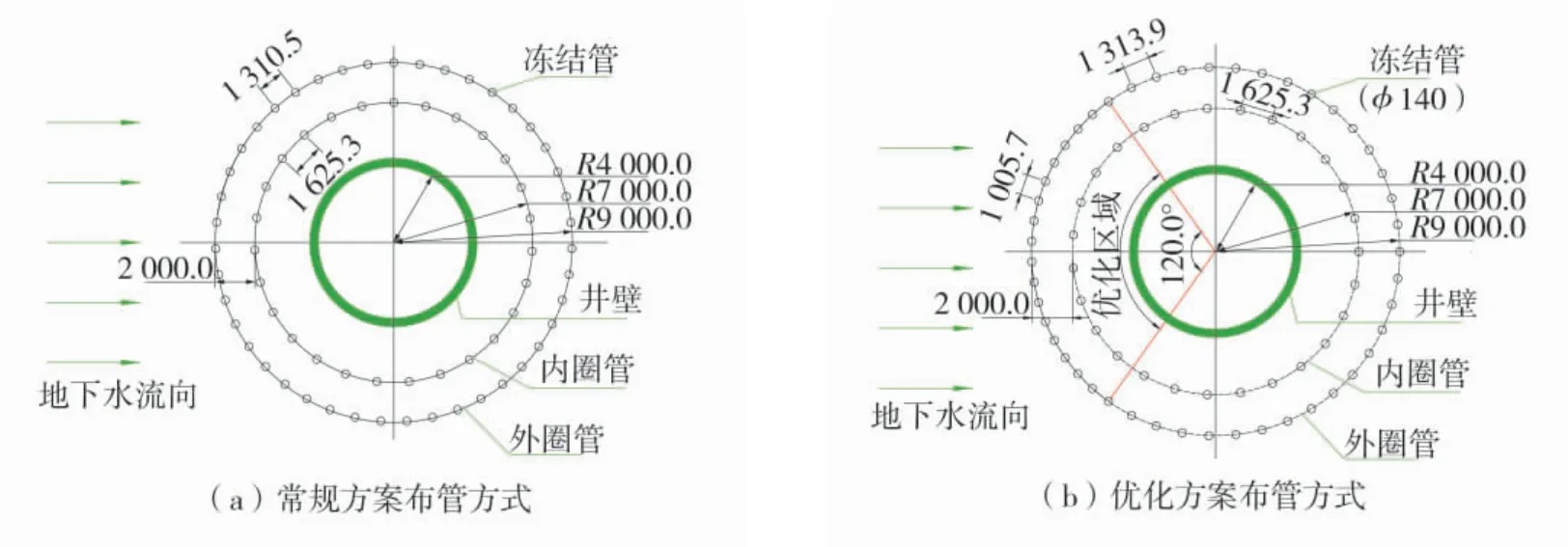
图4 优化前后冻结管的布置方式Fig.4 The arrangement of the freezing pipes before and after optimization

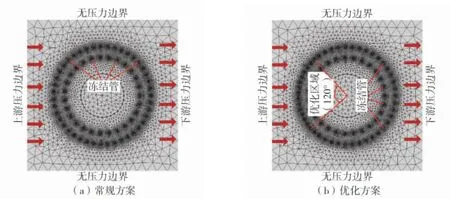
图5 常规方案与优化方案的数值计算模型Fig.5 Numerical calculation model of conventional scheme and optimization scheme

3.2 优化效果

根据饱和砂土的冰点试验结果，认为冻结砂土层达到-1 ℃时即形成有效的冻结壁，因此-1 ℃等温线即为冻结壁的轮廓线，将优化前后的不同流速的地下水作用下冻结温度场在30、60、90 d 的分布规律绘制成图，常规方案与优化方案温度场分析如图6。

由图6 通过分析发现：在流动的地下水作用下，下游区域的冻结壁的交圈时间早于上游区域，当冻结时间达到90 d 时，下游区域的冻结壁厚度明显大于上游的冻结壁。其主要原因是：地下水在通过上游冻结管作用区域流向下游区域时，通过对流传热作用将上游区域的冷量携带至下游区域，在冷量的叠加作用下，下游区域的冻结速率增加，因此其交圈时间要早于上游区域；与此同时，部分水流在绕过冻结区域流向下游的过程中，也会将上游、以及两侧冻结区域的冷量携带至下游区域，因此下游区域的冻结壁厚度要大于其他位置。

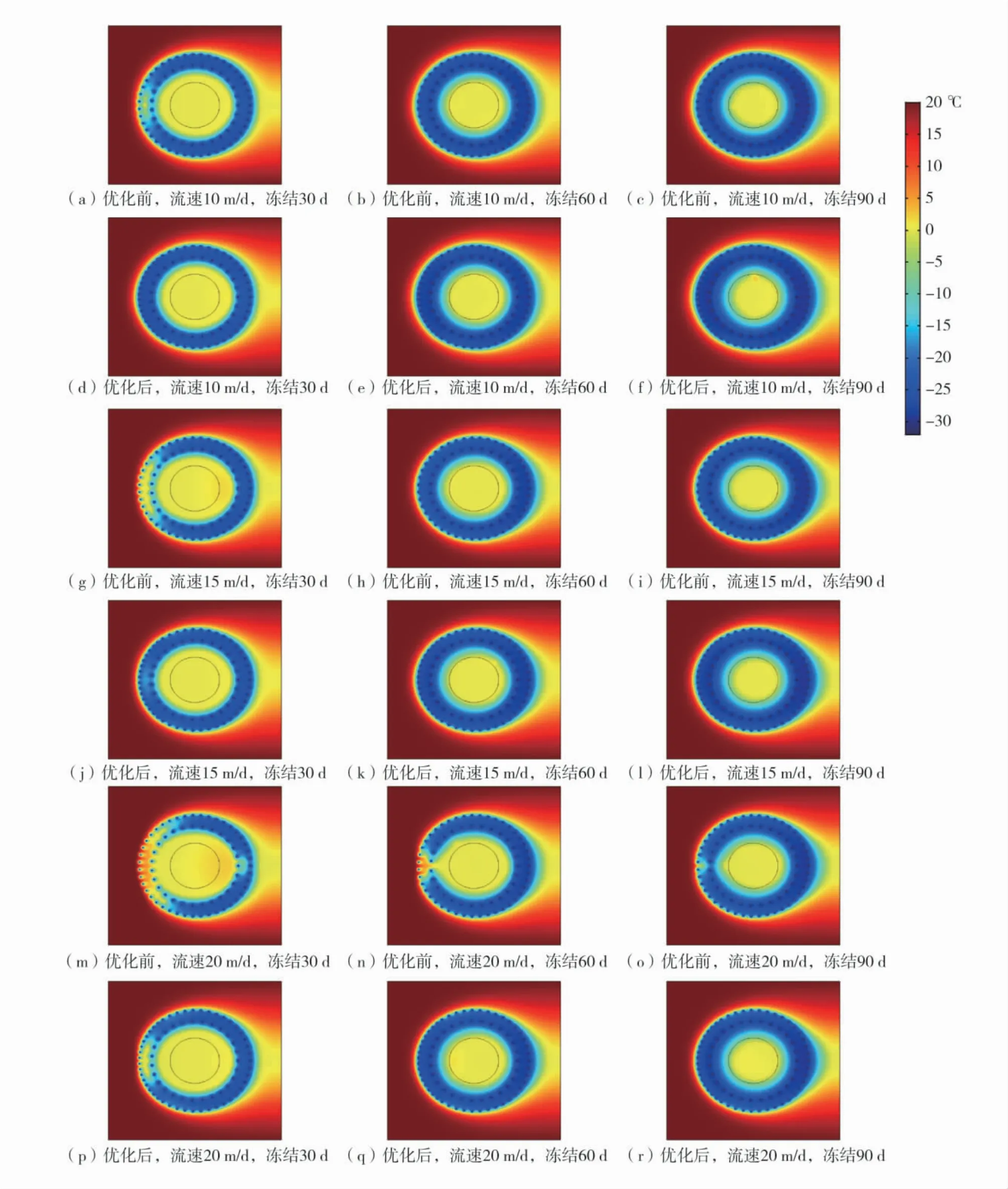
图6 常规方案与优化方案温度场分析Fig.6 Temperature field analysis of conventional scheme and optimization scheme

对冻结方案进行优化，即对上游120°的区域的冻结孔进行加密后，优化区域冻结壁的发展速度明显提高，在相同的冻结时间内，优化后的冻结壁上游位置的冻结范围明显大于优化前的冻结范围，并且地下水流速越大，冻结范围的差别越明显。以内、外圈冻结管均形成完整冻结壁为冻结壁完成交圈的判定标准。常规方案与优化方案的冻结壁交圈时间随流速变化的对比情况如图7。

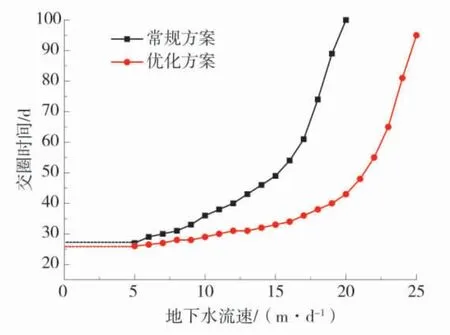
图7 冻结壁交圈时间随流速变化的关系Fig.7 Relationship between the closure time of frozen wall and the flow rate

由图7 通过分析可以发现：2 种方案的冻结壁交圈时间均随着地下水流速增加而增加，并且在地下水流速达到15 m/d 后，冻结壁交圈时间随流速增加明显延长；地下水流速为10、15、20 m/d 时，常规方案的交圈时间分别为36、49、100 d，优化方案的交圈时间分别为29、33、43 d，优化方案相较于常规方案在3 种流速下的冻结壁交圈时间分别提前了7、13、57 d，因此优化方案相较于常规方案可以有效缩短冻结壁交圈时间，并且流速越大，优化方案对冻结壁交圈时间的改善越明显。

当冻结时间达到90 d 和120 d 时，常规方案和优化方案冻结壁的厚度随流速的变化规律如图8。

由图8 可以发现：冻结90 d，地下水流为7、13、19 m/d 时，常规方案的冻结壁厚度分别为6.74、6.05、5.01 m，优化方案的冻结壁厚度分别为6.76、6.15、5.34 m，优化方案相较于常规方案的冻结壁厚度分别提高了 0.02、0.10、0.33 m；冻结 120 d，地下水流为9、15、21 m/d 时，常规方案的冻结壁厚度分别为7.00、6.68、5.63 m，优化方案的冻结壁厚度分别为7.04、6.73、6.20 m，优化方案相较于常规方案的冻结壁厚度分别提高了0.04、0.05、0.57 m。因此可知，随着地下水流速的增加，冻结壁的厚度整体呈减小的趋势；对应相同的地下水流速，优化方案形成的冻结壁的厚度明显大于常规方案的冻结壁，并且随着地下水流速的增加优化方案的效果越明显。

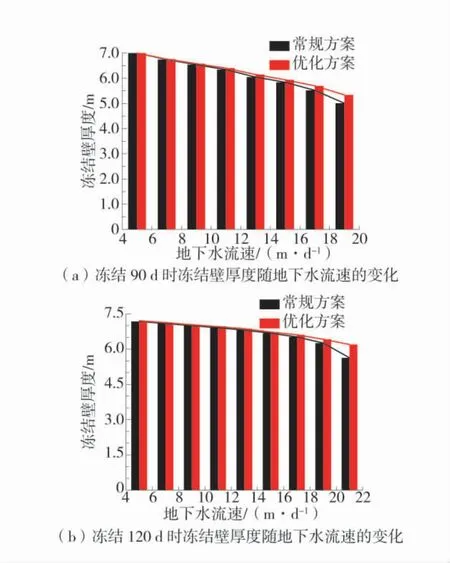
图8 冻结壁厚度随地下水流速的变化情况Fig.8 Variation of the thickness of frozen wall with the flow rate of groundwater

综上，在大流速地下水作用下，通过在对双圈冻结管布置方案中的上游位置的冻结管进行加密可以有效缩短冻结壁的交圈时间、增大冻结壁的厚度。产生这种效果的主要原因是，在较大流速的地下水作用下，冻结管布置圈的上游位置的冻结效果是影响整个冻结壁交圈时间以及厚度的决定性因素，对上游位置的冻结管进行加密处理后，增加了上流区域的冷量供应，缩小了相邻冻结管之间的间距，从而缩短了上游区域的冻结壁的交圈时间，进而提高了整个冻结壁的冻结效率。

4 结 论

1）通过对上游120°范围内冻结管进行加密的方式对常规冻结方案进行了优化设计。当地下水流速为10、15、20 m/d 时，常规方案的交圈时间分别为36、49、100 d，优化方案的交圈时间分别为 29、33、43 d，优化方案相较于常规方案在3 种流速下的冻结壁交圈时间分别提前了7、13、57 d，因此优化方案相较于常规方案可以有效缩短冻结壁交圈时间，并且流速越大，优化方案对冻结壁交圈时间的改善越明显。

2）在较大流速的地下水作用下，冻结管布置圈的上游位置的冻结效果是影响整个冻结壁交圈时间以及厚度的决定性因素，对上游位置的冻结管进行加密处理后，增加了上流区域的冷量供应，缩小了相邻冻结管之间的间距，从而缩短了上游区域的冻结壁的交圈时间，进而提高了整个冻结壁的冻结效率。

3）在对冻结方案进行优化设计的时候，冻结管加密区域的位置以及范围都会对最终的冻结效果产生显著的影响，我们将在后期的研究中对该问题进行更深入的研究与分析。