支承压力区裂隙闭合度变化对渗透率的影响

李 立，于 雷，张霜玉，康 强

（1.中国矿业大学（北京）资源与安全工程学院，北京 100083；2.天地科技股份有限公司，北京 100013；3.中煤科工集团国际工程有限公司，北京100013）

研究煤体渗透率对弄清瓦斯流动，保证安全生产等具有重大意义。影响渗透率的因素有很多，包括有效应力、岩石性质、裂隙方向等。众多学者已对此进行了大量研究：姜振泉[1]研究了岩石性质对渗透率的影响，结果发现：软岩的微裂隙在弹性阶段张剪切裂隙即开始发育，硬岩裂隙从塑性阶段才开始发育，裂隙发育导致了渗透率的明显增加。李波[2]通过实验发现了试样的渗透率与围压呈非线性幂函数关系。林海飞[3]通过实验室研究得出了有效应力和渗透率的拟合方程。秦伟[4]通过煤岩固-气耦合试验，研究了在不同的轴压、围压的加卸载情况下煤岩体渗透率的变化规律。李志强[5]通过渗流实验研究了渗透率与温度以及应力的关系。周世宁发现[6]层理方向对煤体的渗透率影响很大，平行层理煤样的渗透率要大于垂直层理煤样，相差可以达10 倍到几十倍。薛熠[7]考虑了煤体开挖后的损伤效应，建立了峰后煤岩体渗透率模型，分析了3 种典型开采方式下渗透率的分布特征。薛东杰[8]利用渗逾模型定量描述了采动裂隙的特征，为建立渗透率与裂隙的定量关系提供了合适的数学载体。李世平[9]通过实验室研究，获取了渗透率在煤样破坏过程中的变化曲线，发现渗透率的变化曲线滞后于应力应变曲线。现场研究方面，汪有刚[10]和邓质刚[11]利用KSE 气体浓度记录仪记录了SF6示踪气体的浓度变化，依此计算出工作面前方不同距离处的渗透率大小。王凯[12]利用钻孔瓦斯流量法研究了采煤工作面前方煤体卸压增透效应，测定了支承压力区内的煤体瓦斯渗透率的演化规律。现场研究所得的煤体渗透率演化曲线具有相似的规律，即从工作面远处靠近工作面的过程中，渗透率缓慢增大后减小，在极限平衡区快速增大。煤体中含有大量的孔裂隙结构，裂隙是瓦斯运移的主要通道。张勇[13]根据瓦斯在裂隙中的流动形式将瓦斯流动通道分为宏观通道和细观通道；周世宁把煤层简化为砖墙结构[6]，认为瓦斯在砖体中的运动属于扩散运动，进入到砖缝属于渗流运动。瓦斯流动以煤体裂隙为载体，因此，煤体裂隙的特征是渗透率的决定性因素。因此，不考虑瓦斯与煤体的相互作用，主要分析煤体裂隙闭合度变化对渗透率的影响；通过裂隙闭合的力学模型，分析了支承压力区裂隙闭合度的变化过程，得出了工作面前方裂隙闭合的区域范围；分析了支承压力区煤体渗透率的演化规律；通过comsol 数值模拟软件，模拟了工作面前方渗透率的演化过程。

1 裂隙闭合度理论

1.1 支承压力区裂隙闭合度力学

支承压力区内应力的变化会导致裂隙闭合度的变化，建立的煤岩体裂隙压实闭合模型如图1，图中θ 为裂纹的方位角，σ1为垂直应力；σ3为水平应力；b、c 分别为椭圆形裂隙的半开度和半长轴。

通过裂隙周围的位移场解析表达式可以得出裂隙闭合的力学条件为[14]：

当σ1≤4G0α/（ζ+1），σ3≤4G0α/（ζ+1），所有的裂隙都张开。

当σ1≥4G0α/（ζ+1），σ3≤4G0α/（ζ+1），部分裂隙闭合。

图1 煤岩体裂隙压实闭合模型Fig.1 Model of crack compaction in coal

当σ1≥4G0α/（ζ+1），σ3≥4G0α/（ζ+1），所有的裂隙都闭合。

式中：G0为岩石的剪切模量；α=Lb/Lc；ζ 为平面应力系数，ζ=3-v/（1+v）；v 为泊松比。

1.2 支承压力区裂隙闭合度演化分析

静水应力条件下垂直应力σ1等于水平应力σ3。

当原岩应力区σ1＝σ3＝ρgH≥4G0α/（ζ+1），则裂隙在原岩应力区全部闭合。式中：ρg 为煤层上覆岩层平均体积力；H 为煤层埋深。

在支承压力弹性区，从原岩应力区至工作面的过程中，σ1逐渐增加，σ3逐渐减小，当满足条件：

此时部分裂隙张开。

在极限平衡区，σ1和σ3均快速卸载，当满足条件：

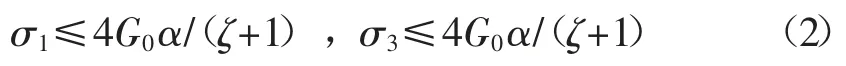
此时，所有裂隙快速张开。

因此，从原岩应力区至工作面，裂隙经历了“完全闭合-部分张开-完全张开”的过程。

当原岩应力区σ1＝σ3＝ρgH≤4G0α/（ζ+1），则裂隙在原岩应力区处于张开状态。

在支承压力弹性区，当满足条件：

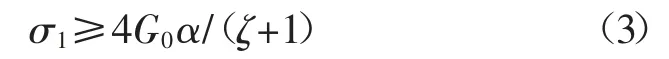
此时，部分裂隙开始闭合。

同样地，在极限平衡区，应力快速卸载导致所有裂隙快速张开。裂隙经历了“完全张开-部分闭合-完全张开”的过程。

1.3 支承压力区裂隙闭合度区域计算

以工作面为原点，开挖方向为x 轴正方向，垂直方向为y 轴，建立坐标系，支承压力区渗透率及裂隙演化如图2。

图2 支承压力区渗透率及裂隙演化Fig.2 Permeability and crack evolution in abutment pressure area

弹性区内支承压力表达式为[15-16]：

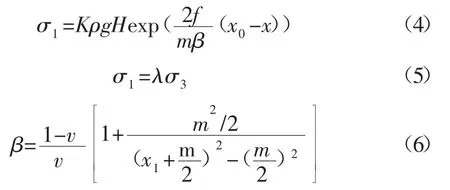
式中：K 为应力集中系数；f 为层面间的摩擦因数；m 为煤采高；x0为峰值点距离工作面的距离；λ为侧压系数，λ＝v/1－v；x1为弹性区宽度。

根据分析，当原岩应力区ρgH≥4G0α/（ζ+1），弹性区内若满足条件（1），部分裂隙张开。结合式（4）、式（5）可求得弹性区内部分裂隙张开的区域范围：

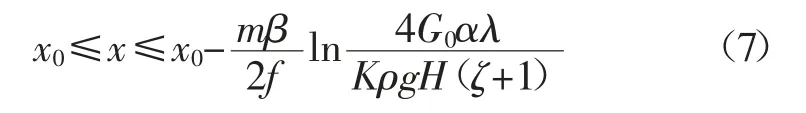
当原岩应力区ρgH≤4G0α/（ζ+1），弹性区内若满足条件（3），部分裂隙闭合，结合式（4）可求得弹性区内部分裂隙闭合范围是：

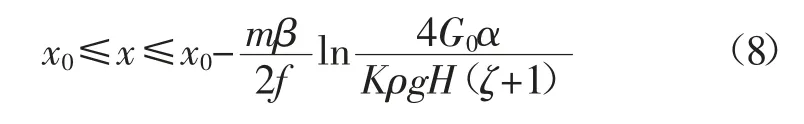
2 支承压力区煤体渗透率演化

渗透率与裂隙闭合度相关，同时还与裂隙的发育相关。裂隙张开导致渗透率增加，裂隙闭合导致渗透率减小，裂隙发育会导致渗透率增加。主要研究裂隙闭合度的变化对渗透率的影响，对裂隙的发育仅做简单介绍：

1）当原岩应力区σ1=σ3≥4G0α/（ζ+1），裂隙在原岩应力区全部闭合。①弹性区内：裂隙闭合度变化为裂隙全部闭合-部分裂隙张开，裂隙张开区域见式（5），导致渗透率缓慢增加，裂隙发育状态为AB段垂直应力缓慢增加，水平应力缓慢减小，裂隙缓慢孤立发育[17]，导致渗透率缓慢增加，BC 段为垂直应力快速增加，水平应力快速减小，裂隙快速发育，次生裂隙大量产生[17]，导致渗透率快速增加；②极限平衡区内：裂隙闭合度变化为所有裂隙突然完全张开，裂隙发育状态为煤体裂隙失稳扩展，形成多个宏观剪切面[17]，裂隙闭合度和发育状态导致渗透率呈“突跳式”增加。因此，可以推断，对于埋藏较深的煤层，原岩应力大，初始裂隙处于闭合状态。煤层开挖后，从原岩应力区到工作面，渗透率经历了“缓慢增加-快速增加-突跳式增加”的过程。

2）当原岩应力区σ1=σ3≤4G0α/（ζ+1），原岩应力区内的裂隙都处于张开状态。①弹性区内：裂隙闭合度变化为裂隙全部张开-部分裂隙闭合，裂隙闭合区域见式（6），导致渗透率减小，裂隙发育状态为AB 段同上文描述，渗透率缓慢增加，BC 段为同上文描述，渗透率快速增加；②极限平衡区内：裂隙闭合度及裂隙发育状态同上文描述，渗透率呈“突跳式”增长。因此，可以推断，对于埋藏较浅的煤层，原岩应力较小，初始裂隙处于张开状态，煤层开挖后，从原岩应力区到工作面，渗透率经历了“缓慢增加-减小-突跳式增加”的过程。

渗透率演化是裂隙闭合和裂隙发育扩张共同的作用结果。裂隙发育扩张和裂隙闭合对渗透率的作用存在竞争关系。一方面，裂隙发育导致渗透率增大，另一方面裂隙闭合导致渗透率降低，根据下文数值模拟结果和相关文献实测结果[10-12]，裂隙闭合虽然导致渗透率减小，但由于裂隙发育扩张作用，仍远大于初始渗透率。

3 数值模拟分析

3.1 模型建立与基本假设

1）几何模型。利用comsol 数值模拟软件，模拟支承压力区渗透率演化规律。数值模拟模型参数见表1，参数根据我国高瓦斯矿井的实际情况，并参考了相关文献设置。2 维几何模型长100 m，高30 m，其中顶板高15 m，煤层高5 m。底板高10 m，数值模拟几何模型如图3。在煤层左边界留10 m 的边界煤块，以消除边界效应。

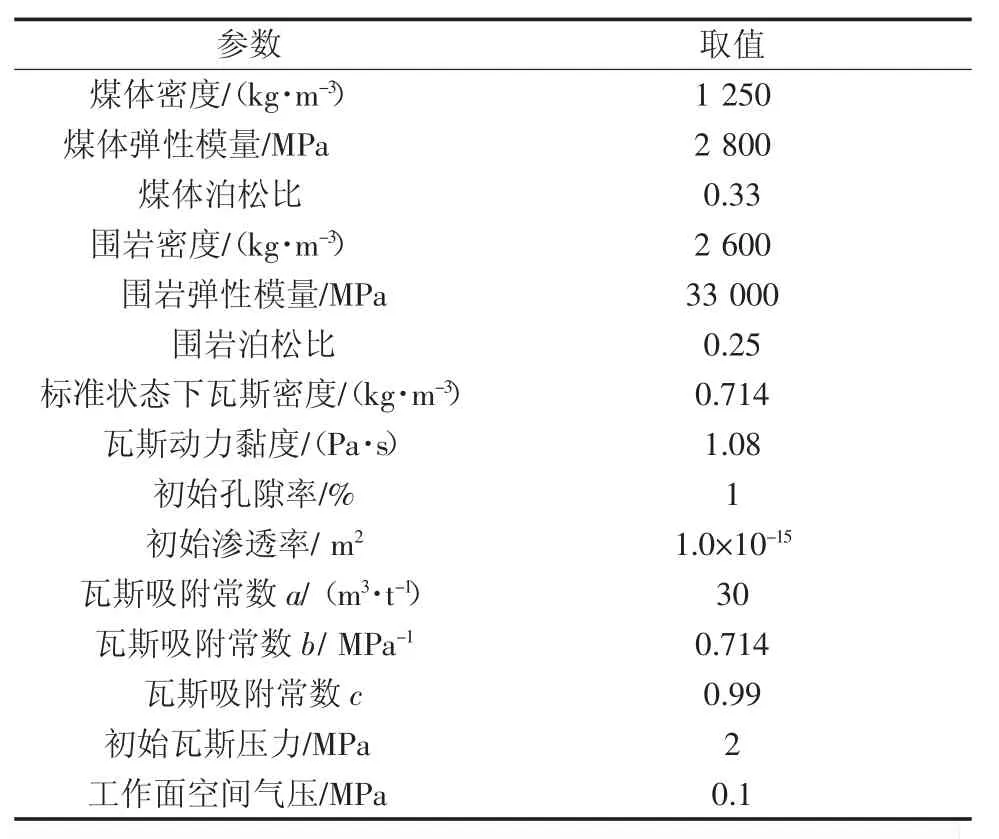
表1 数值模拟模型参数Table 1 Numerical simulation model parameters

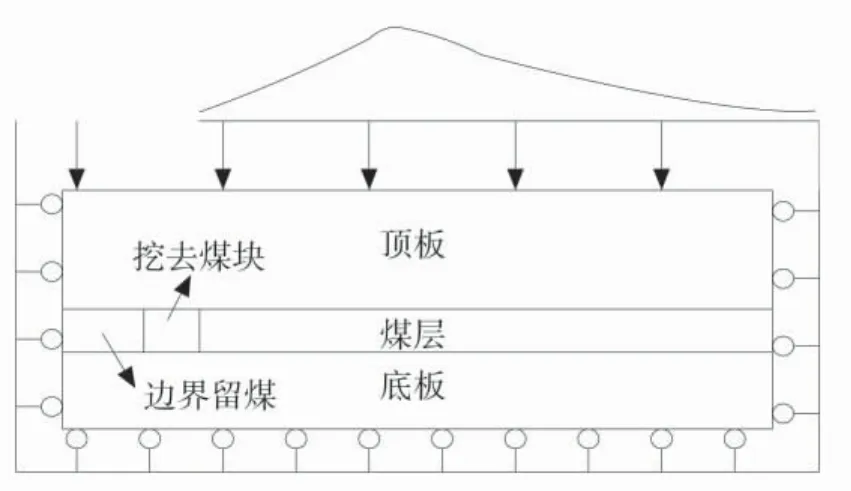
图3 数值模拟几何模型Fig.3 Numerical simulation geometry model

2）边界条件。模型左右两侧和下部边界使用位移边界条件：左右两侧固定x 方向位移为0，下部固定y 方向位移为0，模型顶端设为应力边界条件，设置采深为600 m。

3）数值模拟模块的应用。模型应用了固体力学模块和地球科学模块中的Brinkman 流接口。使用固体力学模块建立煤岩体弹塑性模型，屈服条件满足D-P 准则，将瓦斯压力耦合进固体力学模块本构方程中，对模型赋参数值求解使其收敛，可以求得煤体应力应变值。然后利用地球科学模块中的Brinkman 流接口计算瓦斯流场。

4）渗透率演化规律。根据Kozeny-Carman 方程，可以得到渗透率k 的演化方程[18]：

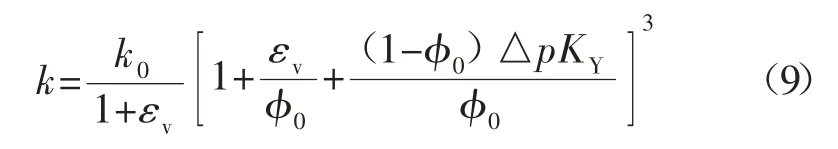
式中：k0为煤岩初始渗透率；εv为煤体体积应变；φ0为煤体孔隙率和初始空隙率；△p 为瓦斯压力改变量；KY为煤体体积压缩系数，KY=3（1－2v）/E，MPa-1；v 为柏松比；E 为弹性模量。

3.2 数值模拟结果

工作面前方煤岩体渗透率和垂直应力分布图如图4。

图4 工作面前方煤岩体渗透率和垂直应力分布图Fig.4 Permeability and vertical pressure distribution in front of working face

由图4（a）可以看出，推进25 m 时，应力峰值点在煤壁前方8 m，峰值应力大小30 MPa。由图4（b）可以看出，开挖后60 s 时，从原岩应力区到工作面，煤体渗透率经历了“缓慢增加-减小-突然增大”的过程：煤壁前方15～50 m 渗透率缓慢增加，煤壁前方8～15 m 渗透率减小，但渗透率仍远大于初始值，约为初始渗透率的 50 倍（初始渗透率 1.0×10-15m2），这是裂隙闭合和裂隙发育扩张共同的作用结果。一方面，煤壁前方8～15 m 范围内，裂隙快速发育，导致渗透率增大；另一方面，此区域内部分裂隙在应力的作用下产生闭合，导致渗透率降低。（根据下文3.3中理论计算结果，裂隙闭合的区域范围是煤壁前方8～17.7 m）因此，此范围内煤体渗透率减小，但由于裂隙发育扩张作用，渗透率仍远大于初始渗透率。

煤壁前方8 m 范围内，也就是极限平衡区内，渗透率产生“突跳现象”，约为初始值的210 倍。

应力的变化速率决定了裂隙发育与闭合度的变化速率，进而决定了渗透率的变化速率。根据数值模拟结果，煤壁前方15～50 m，应力变化较慢，因此渗透率的变化较慢；煤壁前方8～15 m，应力加速变化导致渗透率变化加快；煤壁前方8 m，应力快速卸载，煤体裂隙快速扩展形成更多的剪切破坏面，裂隙突然全部张开导致，导致渗透率产生“突跳”现象。

3.3 理论计算与数值模拟结果对比

根据表1 中参数，结合前文1.1 中裂隙闭合条件，分析裂隙闭合度变化：G0=E/2（1+v）=1.05 GPa，ζ=3-v/（1+v）=2。

煤体中裂隙长度较长，开度很小，取值α=Lb/Lc=1/100；则4G0α/（ζ+1）=14 MPa；σ1=σ3=7.5 MPa；满足σ1≤4G0α/（ζ+1），σ3≤4G0α/（ζ+1）。因此，原岩应力区裂隙都处于张开状态。

根据图4（a），峰值点距煤壁距离x0=8 m；应力集中系数K=3.3；弹性区范围x1=40 m；煤厚m=5 m，取层面间的摩擦因数f=0.3。

根据式（4）可以求出，β=2.04。

将上述数据代入式（6），可以求出裂隙闭合区域范围为：8≤x≤17.7 m。因此，裂隙闭合区域是煤壁前方8～17.7 m，导致渗透率下降。根据数值模拟结果：煤壁前方8～15 m 渗透率下降，理论计算和数值模拟结果一致。

4 结 论

1）原岩应力大时，原岩应力区裂隙处于闭合状态，支承压力弹性区内，裂隙由完全闭合逐渐张开，极限平衡区内，所有裂隙快速张开。渗透率经历了“缓慢增加-快速增加-突跳式增加”的过程。

2）原岩应力小时，原岩应力区裂隙处于张开状态，支承压力弹性区内，部分裂隙闭合，极限平衡区内，所有裂隙快速张开。渗透率经历了“缓慢增加-减小-突跳式增加”的过程。

3）数值模拟结果表明：煤壁前方8 m 范围内渗透率急剧增大，约为初始值的210 倍；煤壁前方8～15 m 渗透率减小，但仍远大于初始渗透率；煤壁前方15～50 m 渗透率缓慢增加。原岩应力区到工作面过程中，煤岩体渗透率经历了“缓慢增加-减小-突跳式增加”的过程。