永丰县藤田镇大坑水库大坝安全评价

黄春财

(江西省永丰县水利局建管股，江西 吉安 331500)

0 引 言

裂缝开度、扬压力、位移、变形和渗流等因素均可对大坝安全产生影响，且大坝运行状态受不同因素的影响程度存在一定差异，对大坝安全水平利用单一因素评价存在较大的不确定性，同时各因素间的关联作用往往具有随机性，因此有必要融合各类不确定信息综合评价大坝的安全状态[1]。张琳等[2]依据评估函数、持续序列和D-S证据理论，基于相关研究资料建立了信息评估模型和可信度函数；李文立等[3]对证据模型在冲突分配过程中加以修正，有效解决了Dempster处理规则中存在的问题；曹杰等[4]将多维空间中的点与基本概率赋值一一对应，用于加权融合计算；毕凯等[5]将聚类分析和模糊数学法相耦合提出一种新的分析方法。目前，关于不同类和同类监测项目间的数据融合研究还鲜有报道，且考虑权重的加权融合法的研究更少。鉴于此，此次对同类项目的监测数据采用变异系数联系，对各项目权重利用欧式距离计算，并对监测数据利用优化的加权融合法求解，对水库大坝的安全状况结合D-S证据理论评价。

1 监测数据预处理

1.1 标准化处理

各项初始数据因量纲和量级的不同无法直接参与计算，为消除各效应量之间的不可通透性和避免数量级悬殊对评价结果的影响，有必要无量纲化处理各原始监测数据，具体如下：

1)对于数值越小则水库大坝安全性能越高的坝体渗流、坝基扬压力等监测项目，利用如下公式处理原始监测数据，即：

(1)

2)对于数值越适中则水库大坝安全性能越好的径向位移、切向位移等监测项目，采用下述公式对原始监测数据处理，即：

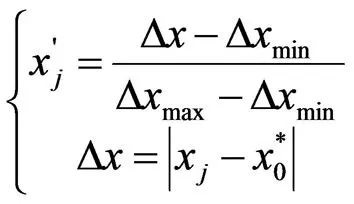
(2)

3)对于数值越大则水库大坝安全性能越好的监测项目，根据计算式(3)处理其监测数据，其表达式为：

(3)

1.2 监测数据归一化

(4)

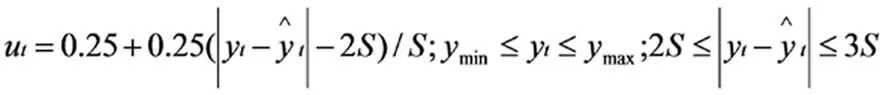
(5)

(6)

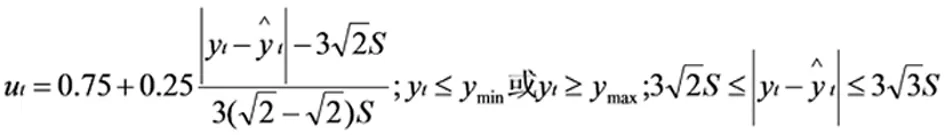
(7)

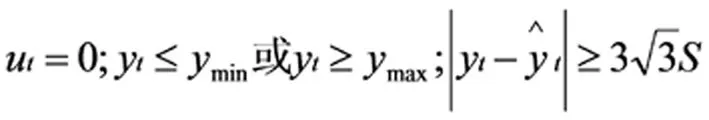
(8)

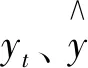
1.3 变异系数赋权法

针对同一测点存在多组监测数据且含有较多测点的项目，采用变异系数法对同测点数据间权重赋值。例如，对于布置了m个测点且每个测点存在n个测值的坝顶水平位移监测项目，利用下式计算确定测点i的变异系数δi，其表达式为：

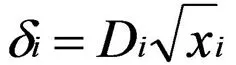
(9)

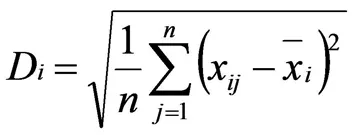
2 D-S证据理论

集合与命题之间的对应关系按照证据理论中的信任函数确立，而信任函数的规则更新主要通过D-S合成规则实现，在解决处理不确定数据融合冲突时具有较强的适用性。实际应用过程中采用层次分析法和系统工程理论，确定评价因素并建立隶属函数，然后对各因素的基本概率分配函数利用隶属函数计算，总的概率分配和最终评价等级依据D-S准则合成确定。

2.1 建立评价因素集

裂缝开度、位移、渗流和扬压力等为影响大坝安全的主要因素，在大坝安全评价中建立的因素集为U={u1,u2,…,un}，选取的因素要综合反映大坝的深层滑移、强度、稳定性等状态。依据监测信息的取值范围和大坝安全检查实施细则，文章结合水库大坝运行实际情况和相关文献资料将安全评价标准划分4个等级，由此构建的模糊评价集为：

V={V1，V2,V3,V4}={不安全，较不安全，较安全，安全}

(10)

式中：Vi为评价体系中的某指标的安全状态；V为水库运行的安全识别等级框架。各评价因子和不同等级之间的联系利用隶属度区间建立，当前还未形成普遍适用的等级划分标准，等区间划分法为当前系统工程的常用方法。本研究采用等区间划分法确定大坝安全评价等级，具体见表1。

表1 大坝安全分级标准

2.2 概率赋值法计算

对不确定性、模糊性信息利用D-S证据理论融合，需要采用隶属函数获取基本概率分配函数，然后对监测信息赋予相应的数值。为满足运算简化和数据后期分区的要求，隶属函数值μA(x)按照三角形模糊式计算确定，其表达式如下：

(11)

式中：a、b、c为划分的区间界限值。

根据表1识别框架和隶属函数形式，将大坝安全监测项目的概率赋值设定为隶属度，计算式如下：

(12)

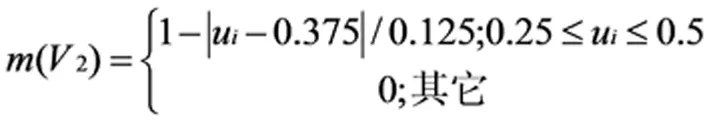
(13)

(14)

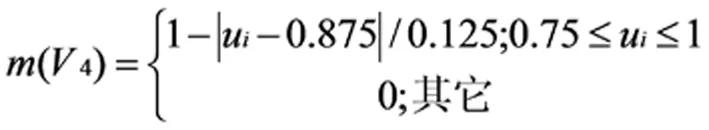
(15)

式中：ui为标准化处理后的监测项指标值；m((Vi)为不同评价等级下各指标的概率赋值，大坝安全监测项目的测量值趋近于属性特征中心值的程度越高，则对应的目标BPA越大。

2.3 概率赋值的融合

(16)

式中：A、Φ为集合和空集；m1(Vi)、m2(Vj)为安全评价因子的两个概率赋值函数；K为衡量信息冲突程度的标准，若K≤1则认为信息间存在冲突，无法融合；若K≠1，则认为能够融合信息。

根据以上规则融合的不确定信息具有较差的鲁棒性，即融合结果受基本概率赋值的影响较为显著，当存在赋值为零的情况下焦元概率值无法为零，信息融合具有“一票否决”的属性。因此，文章对证据融合提出一种欧式距加权改进的方法，设两个点在n维欧式空间内为A(x1，x2，…，xn)、B(y1，y2，…，yn)，则利用欧式公式确定该两点的距离D(A，B)为：

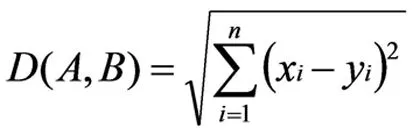
(17)

n维欧式空间中不同的点视为大坝安全评价指标，以向量的形式x=(a1,a2,…,an)、y=(b1,b2,…,bn)对坐标mi(A1)=a1，mi(A2)=a2，…，mj(An)=an；mj(B1)=b1，mj(B2)=b2，…，mj(Bn)=bn进行转变处理。两证据间的距离d(m1,m2)利用欧式距离计算式确定，即：

(18)

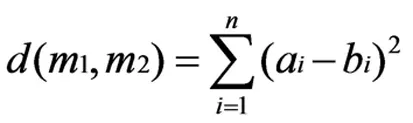
3 实例分析

大坑水库位于永丰县藤田镇藤田河左支中西山水上游，该水库是一座集灌溉、防洪、养殖、供水等功能于一体的小(2)型水利工程，设计和实际灌溉面积分别为100hm2和66.7hm2。经三十多年的服役运行，工程设施不配套、年久失修、建筑物老化等问题突出，枢纽工程现已无法满足正常运行要求。对此，永丰县水利局对大坑水库大坝进行安全监测，监测项目有裂缝开度、水平位移、垂直位移、扬压力和渗流，经现场检查枢纽工程和走访调查水库运行管理、施工、设计等情况，确定了其病险隐患，具体如下：

1)该水库枢纽工程坐落在第四系残坡积层之上，岩石破碎，构造发育，坝顶宽5.5m，大坝上游坡为1∶2.0，无护坡，下游坡为1∶2.0，无坝面排水系统，未做滤土排水设施。该大坝属于均质土坝，土体松软，见多处冲沟，坝体土主要是风化料，含大块径风化岩块。坝体蚁害严重，1/4坝高以下坝坡及坝脚沿线见湿软散浸区，主河床部位渗流明显，坝脚沿线见大面积沼泽地；当库水位达到200.44m高程以上时大坝渗漏更为明显，左坝段199.44m高程处见集中渗漏点；坝肩山体破碎，左坝肩1/2坝高处见集中绕坝渗漏,坝体、坝肩、坝基渗漏严重。

2)溢洪道位于坝右的天然亚口内，地基为震旦系凝灰质千枚岩，岩体呈全强风化，岩石破碎，边坡稳定性差，局部塌方；溢洪道开敞式宽顶堰体，设计宽度3.8m，实际宽3.8m，陡槽底板和边坡无衬砌，冲刷严重，无消能设施，无排洪渠，泄洪时冲毁下游农田[6]。

3)斜管断裂、消力池破坏漏水严重，平涵管预制混凝土平涵接缝砂浆脱落，与坝体存在接触渗漏[7]。

4)水库由水面经营人员兼管，无管理制度，管理不规范，。无水、雨情观测设施，无通讯设施[8。

采用ARMA预测模型和某一时间段内大坑水库监测数据，按照监测资料拟合值科学评价大坝安全状态。

3.1 数据前期处理

设U={u1,u2,u3,u4,u5}={渗流，扬压力，垂直位移，水平位移，裂缝开度}为监测数据因素集，然后利用文中所述归一化、标准化公式对各项监测数据进行处理，从而获取10个监测点的标准值，见表1。在上下游、左右方、上下方同一测点同一时刻的裂缝宽度监测项目存在3个数据，其它项为1个，所以需要采用变异系数法对裂缝开度监测值赋权。

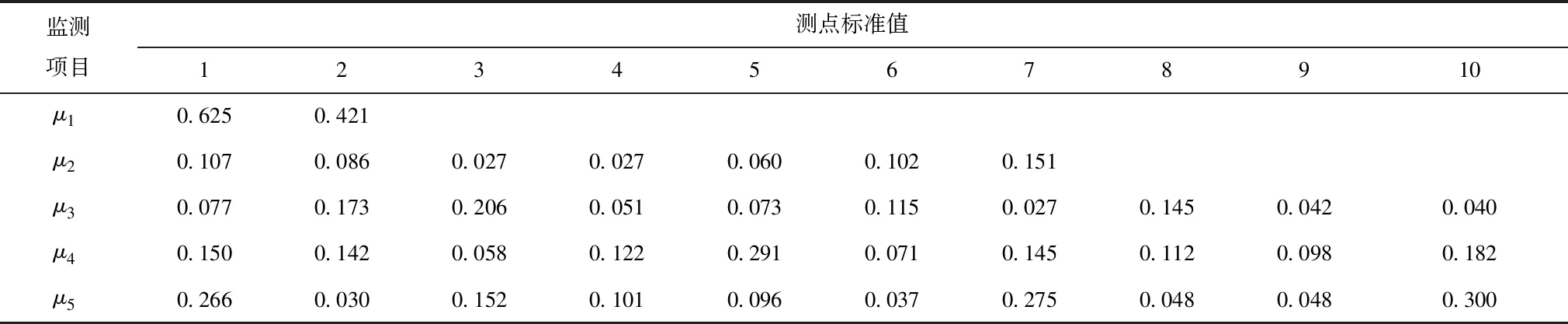
表1 大坝安全监测项目标准值

3.2 基本概率赋值

根据基本概率赋值计算公式和各监测项目标准化值，求解出水库大坝安全评价最底层赋值，然后对基本概率赋值的权重及其距离按照公式(18)和响应的流程求解，从而确定包含多个测点的每一种监测项目概率赋值，通过融合计算确定存在多个测点的项目赋值，如表2。

表2 融合计算的基本概率赋值

从表2可知，大坝安全融合值隶属于较安全V3的指标为0.048，除不确定因素外较安全V2和安全V1指标的融合值为0.527，总体融合值的50%以上为较安全和安全等级，因此可认为该大坝处于安全状态。然而，由于不确定度概率赋值还位于较高水平的0.426，所以要获取更加准确的评估结果需要扩大融合的底层指标数，综合考虑其他检测资料提高评价结果的可靠性。从单项指标的角度分析，坝基渗流的概率赋值为0.495，属于不安全的程度较高，可见大坝面临着渗流安全隐患，必须采取有效的安全措施提高坝基渗流稳定性。采用时间序列预测前期数据时，可以保证评价结果的可靠性，但无法进行长期的预测，若进一步提高融合精度需要考虑其他更多的监测信息[9]。

4 结 论

1)文章对D-S证据理论利用加权融合法加以优化，从而建立了数据与信息对象将的联系。对监测信息指标权重利用欧式距离公式求解，采用变异系数赋权法处理同一测点的多组监测数据，可实现直接融合不同测点数据的目的。

2)对永丰县藤田镇大坑水库大坝安全状态采用加权优化的D-S证据理论评价，评价结果与工程实际情况基本相符，可见该优化方法具有较高的可靠性和可行性。