低碳钢疲劳损伤声发射检测的概率熵研究

李建宇，贾中汇，齐 刚,

(1.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津科技大学机械工程学院，天津 300222；2.孟菲斯大学机械工程系，孟菲斯 TN38152)

材料和结构的疲劳是公认的在正常服役条件下引起机械部件或结构失效的最主要原因[1]，关于认识和控制疲劳的研究始终是工程界和学术界普遍关注的课题.由于影响疲劳的因素异常复杂，时至今日，试验方法仍然是关于疲劳最为可靠的研究手段，各种疲劳预测理论和抗疲劳设计准则均基于疲劳试验建立[2].随着人们对疲劳机理的更深入理解以及工程中对疲劳控制的更精确要求，疲劳试验的内涵和要求也不断拓展提升.早期研究中关于疲劳失效研究的重点是对材料和结构疲劳寿命的研究，为此利用试验方法获得疲劳极限和疲劳寿命曲线是关于疲劳寿命研究的核心任务，如经典的S-N 曲线和ε-N 曲线[3-4]；随后，在认识到疲劳总寿命可进一步划分为裂纹萌生、裂纹扩展和断裂等阶段后，疲劳试验的内容又增加了对微裂纹观测以及裂纹扩展速率等的监测，包括显微镜以及超声波探伤、红外检测和金属磁记忆等无损检测技术被广泛用于疲劳的检测[5-8]，这些工作在疲劳裂纹及其扩展的检测方面贡献突出，但是由于检测机制与测量精度等条件的限制，对于疲劳前期即裂纹萌生阶段前材料的微损伤累计的评估与检测鲜有触及.近年来，随着从微细观角度对疲劳损伤演化机理理解的发展需求，疲劳试验的内涵又拓展为对疲劳裂纹萌生阶段材料微结构和微损伤演化的有效观测，例如非线性超声、声发射和各种基于电磁原理的检测技术等[9-10]在材料疲劳微损伤累积的检测上都得到了有效应用.

在众多的损伤检测技术中，声发射技术(acoustic emission，AE)由于其对微小损伤事件的高敏感性和检测的便利性，在疲劳微损伤检测应用中被逐渐重视，如文献[11-12]研究计数、幅值及能量等声发射参数与疲劳损伤及循环加载周次数间的关系.声发射检测往往激发海量数据，一方面说明利用声发射可以获得非常丰富的微损伤信号，另一方面，海量数据也为数据处理和信息提炼增加了难度.虽然已有包括参数分析法、模态分析法和小波分析法等[13-15]关于声发射信号的研究，但多数工作仅限于少量、局部的声发射数据，大量的数据被搁置，没有为认识损伤机理做出更大贡献.对此，文献[16-18]提出利用统计学的手段对海量声发射数据进行统计分析，从而从整体的角度获得相关的损伤演化规律.该方法已在骨水泥、铸铁、纸等材料的微损伤评估中得到有效应用[19-21].本文拟在此基础上，进一步研究用于金属材料在整疲劳历程前期的损伤累积检测和评估，从而为利用试验手段对疲劳裂纹萌生阶段的微损伤演化研究提供一种新的思路.

1 材料与方法

金属材料经循环加载后，包括微观结构等材料属性都会发生变化，例如材料的宏观力学性能(如弹性模量、屈服强度、抗拉强度等)、物理学性能(如电阻率、磁导率等)等[22].材料属性的变化与循环加载次数之间的相关性为疲劳损伤及其演化的测量提供了可能.通过分析不同循环加载次数后，试样在拉伸试验过程中其AE 信号的统计性特征差异，从而寻求金属材料疲劳损伤及其演化的一种探索性的测量和评估方法.

1.1 试验材料

试验材料为工程常用低碳结构钢Q235.其主要成分为：C 0.200%、Mn 0.270%、Si 0.023%、B 0.023%、P 0.016%；力学性能为：抗拉强度 488 MPa，屈服强度 332 MPa，延伸率 22%.为便于声发射检测，试验采用板材试样，几何尺寸如图1 所示.

图1 板材试样尺寸(mm)Fig.1 Geometry of plate specimen(mm)

1.2 试验方案

试验过程如图2 所示，试验分为两个阶段，第一阶段对试样进行循环加载，第二阶段对试样进行静态拉伸，同时采集声发射信号.按照循环加载次数将试验分为六组，第一至第五试验组分别将试件疲劳加载2×105、3×105、4×105、5×105、6×105个周次，另设置无疲劳加载的纯单轴拉伸作为对照组(第六试验组).每组试验试样数为8 个.为指导疲劳试验的参数设定，使用MTS E45 型拉伸试验机对批次试样进行一组预拉伸试验，拉伸速率设定2 mm/min，试验测得试样平均抗拉强度 480 MPa、平均屈服强度340 MPa、平均伸长量9.764 mm.

预先进行整寿命疲劳试验，疲劳试验设置：CIMACH PLS-200 型电伺服液压疲劳试验机采用载荷控制方式，设定试验循环应力水平 σa＝±200 MPa，应力比为-1.试验结果显示，试样寿命主要分布在7×105～9×105次.

AE 采集参数设置：AE 数据采集系统使用PAC公司Micro-Ⅱ Digital AE System，门槛值35 dB，前置放大器增益40 dB，带宽100～400 kHz，采样率1 MSPS，PDT ＝300µs，HDT ＝600µs，HLT ＝1 000µs；谐振式传感器Nano30，谐振频率140 kHz，带宽125～175 kHz，两枚传感器分别布置于试样正反两面轴线上，各距中心线20 mm.

图2 试验过程示意图Fig.2 Schema of experimental protocol

2 结果与讨论

2.1 断面微观结构观测

为在微观层面了解材料损伤的结构变化，采用德国ZEISS 公司SIGMA 300 型扫描电子显微镜对试件断口进行观测，部分结果如图3 所示.

由图3 可知：试样的轴向拉伸断裂使断口存在大量塑性形变特征，脆性断裂特征并不明显.在所有断裂面上，均分布着尺寸范围＜5µm 且大小不等的微孔穴.微孔穴变化与聚结的演化过程将会在拉伸应变的影响下持续进行，伴随材料性能逐渐弱化，并最终导致塑性断裂.相比于对照组，历经6×105次循环加载后，断面上所展现的尺寸大于2µm 的微孔穴产生了显著增长.值得注意的是，在超过4×105次疲劳循环试验组的SEM 图像中(图4 所示)，均观测到了明显的由微孔穴聚结形成的微裂纹，且具备显著的扩展伸长趋势.

图4 SEM图像微孔穴聚结微裂纹及其扩展趋势Fig.4 SEM fracture morphologies of microcracks from microvoids coalescence and their propagation tendency

2.2 声发射原始信号

作为比较，给出对照组与第五试验组的原始AE信号，如图5 所示.在循环周次相差较大的两组试验中，其原始AE 信号特征具有相似性，在弹性阶段(Ⅰ)内，基本没有信号；至屈服点附近(Ⅱ)，信号涌现且有明显的幅值增长；在塑性变形阶段(Ⅲ)，信号集中涌现，且幅值基本低于上一阶段；经过抗拉极限点后(Ⅳ)，信号数量逐渐减少，活性较差；而在最终断裂阶段，仅出现少量、高幅值信号.由此可见，基于试验中的AE 原始信号特征难以直接用于区分不同程度的疲劳损伤，此时利用统计学方法对其进一步分析显得很有必要.

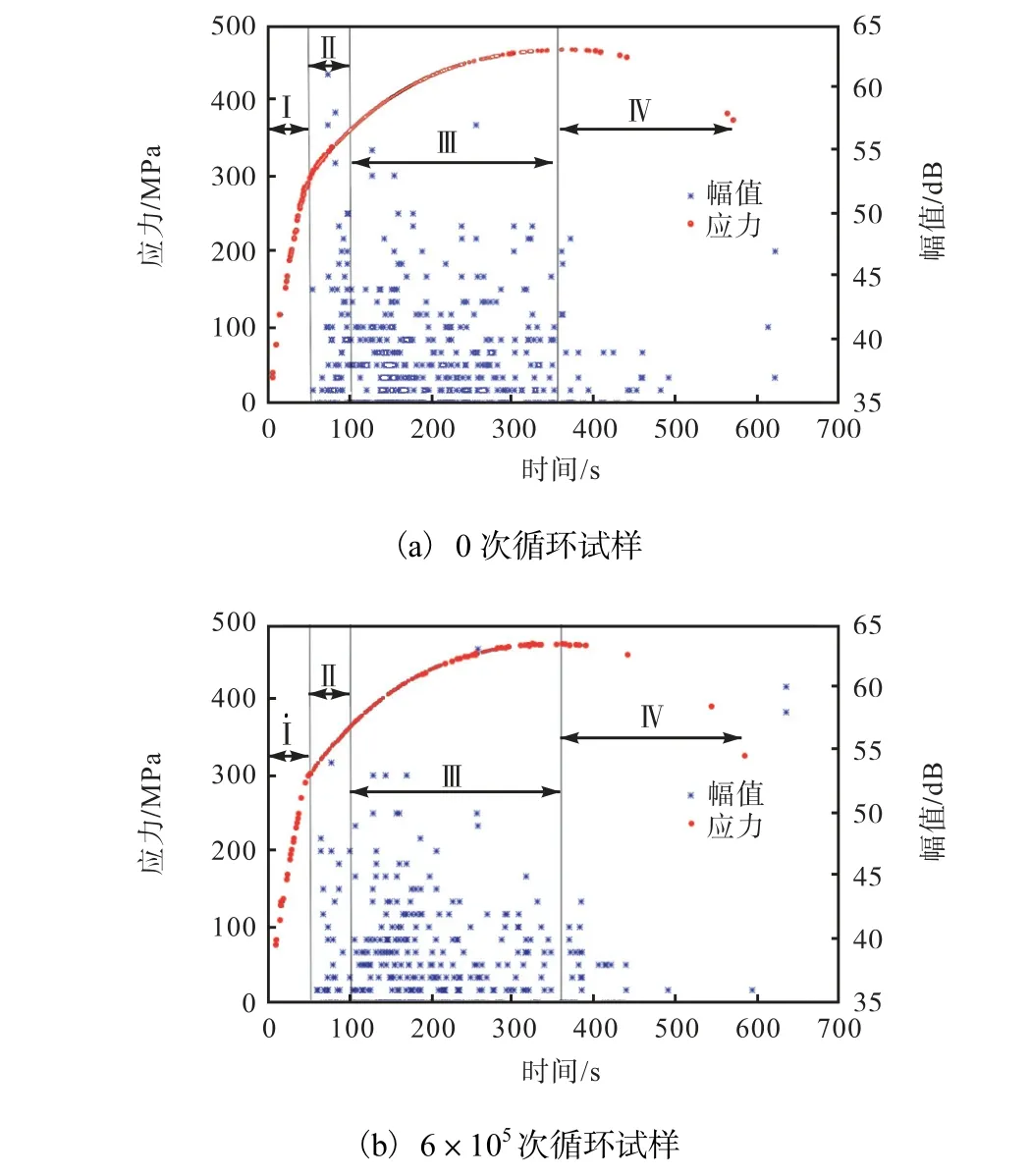
图5 单轴拉伸载荷下试样应力、声发射信号幅值与时间的关系Fig.5 AE signal amplitude-stress-time plot of fatigue specimen under uniaxial loading

2.3 声发射信号的统计分析

材料在受载过程中的声发射现象具有随机性和不确定性.一方面，这是因为材料内部微结构、微缺陷的随机性和不均匀性导致受载后声发射源的随机性；另一方面，由于材料在微观层面的不均匀性和各向异性，导致AE 信号在材料内部的传播过程具有不确定性.此外，材料受载过程中采集到的AE 信号极其丰富，因而涉及到对海量随机数据的分析和处理.基于上述考虑，本文采用统计学方法研究所采集到的AE 信号.

首先，基于AE 事件与微损伤事件的对应关系，利用受载过程中所采集到的AE 信号特征参数(时间、幅值、能量等)，定义材料随机损伤事件[17-20]

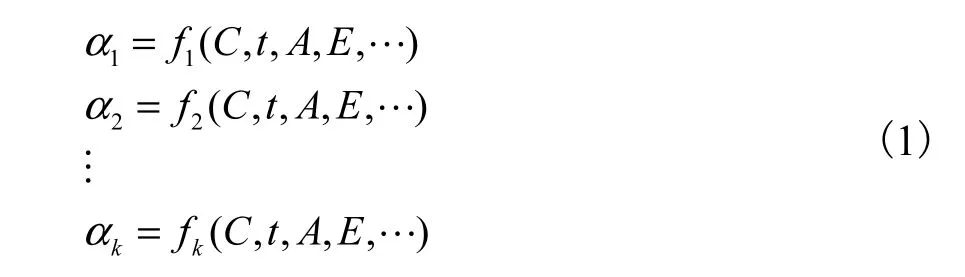
式中：αk代表材料内部的损伤事件；t、A 和E 分别为损伤发生的时间、幅值和能量；C 为信号源的空间坐标.

其次，对某一时间段内的AE 事件进行统计，为说明问题而又不失一般性，选取AE 信号的幅值特征进行统计分析.将AE 幅值从门槛值Amin到最大幅值Amax等分为n 个子区间，称每一区间为尺度标准X.

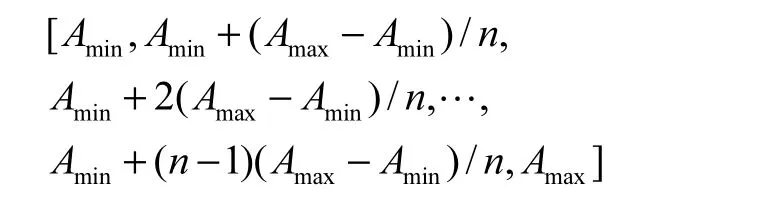
材料损伤演化主要由外部载荷推进，故选取应力作为观察索引Y，从而根据索引宽度的大小确定观察索引Y 的区间数量m.本文数据处理过程所划分的观察索引和尺度标准为：观察索引长度60 MPa、观察索引个数10、尺度标准范围35～65 dB、尺度标准个数10.

最后，对采集得到的AE 信号(每组试验所包含的8 个试样所得数据归为一组进行处理)按上述尺度标准(幅值区间H)与观察索引(应力区间W)划分进行统计计数处理，过程如图6 所示.

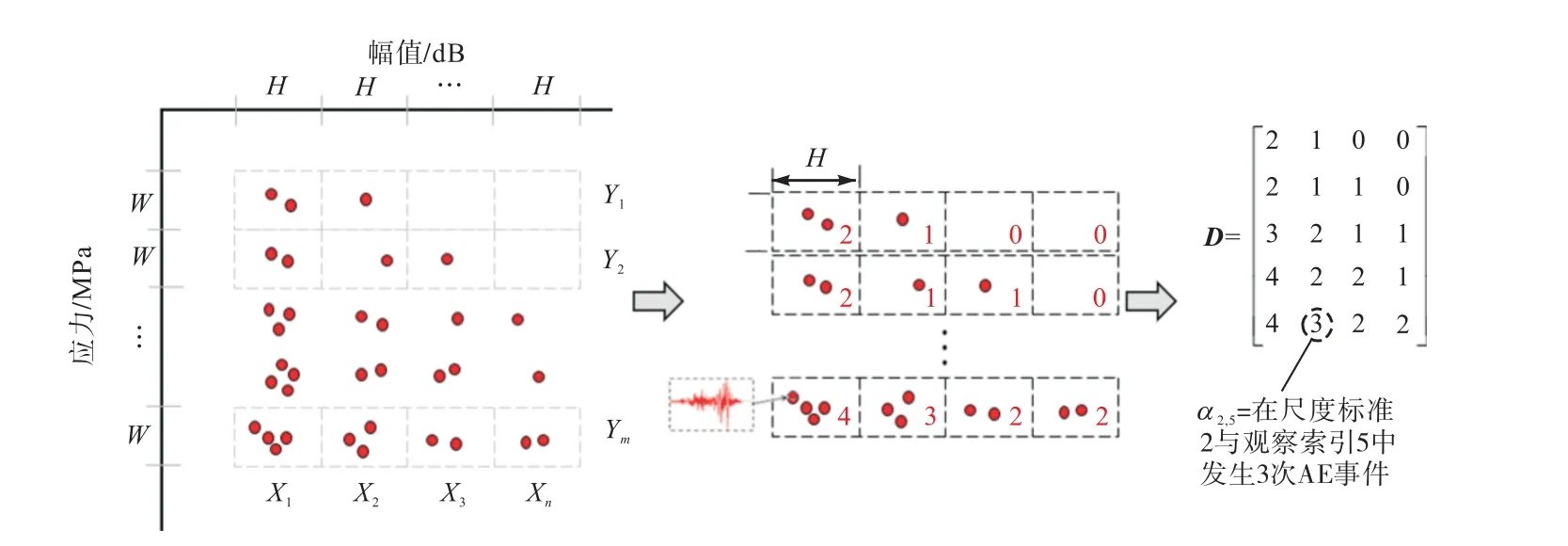
图6 声发射数据的统计计数过程Fig.6 Procedure of AE data statistical counting

则按照上述办法，试样在拉伸过程中的声发射信号可以转化为一个二维矩阵，记为D 矩阵[19-20].

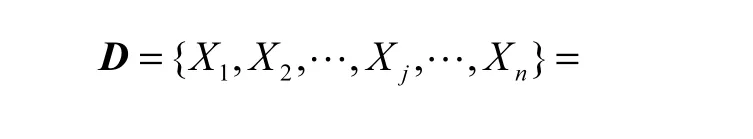
D 的元素αij代表同时落入对应尺度标准与观察索引区间内的AE 事件计数，即材料随机损伤事件数.该矩阵可表达为列向量集合{Xj}或行向量集合{Yi}的形式，列(尺度)向量Xj表示不同应力区间下第j 个幅值区间内的AE 信号数，行(观察)向量Yi表示不同幅值区间内第i 个应力区间内的AE 信号数.

针对行向量Yi，还可以进一步绘制如图7 所示的AE 信号幅值统计分布图，以具体反映随机损伤事件的载荷、数量、幅值和发生率的相互耦合关系.由此可见，早期加载阶段，低幅值AE 信号在数量上占主导，随着载荷的增加，高幅值AE 信号的数量逐渐增加.为了量化随着载荷的增加，AE 信号依照幅值统计分布的变化情况，此处引入损伤概率熵[23]

式中：n 为D 矩阵所划分的尺度标准数；pj为随机损伤事件落入第j 个子区间的概率.

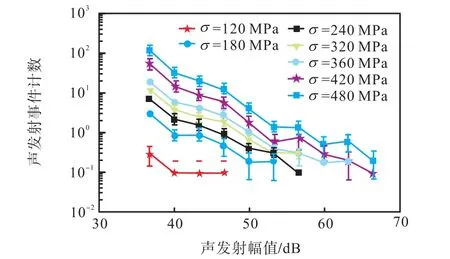
图7 声发射信号幅值统计分布图Fig.7 Statistical distribution plot of AE signal amplitude

研究概率熵值在不同应力条件下的变化规律，并定义为材料的损伤状态轨迹曲线[19-21]，该曲线可作为从宏观角度对材料损伤演化过程的统计性综合评定.具体的，根据概率熵的意义评估材料在载荷作用下损伤演化的不确定性，若熵增，则表示某一或有限尺度区间内AE 信号产生分布的不确定性(比如幅度大小、空间位置、数量等)的增加，预示着与之对应的微损伤事件发生的可能性增加.

2.4 不同循环次数下试样的损伤状态演化分析

按照上述思路，依据公式3 计算各组实验数据在各应力条件下的概率熵值，并将其沿应力序列依次连接，则可以给出各试验组数据对应的损伤状态轨迹曲线，如图8 所示.由图8 可见，各组曲线的基本形状与走势相近.基于试件源自同批次材料，表明在相同条件下的单轴拉伸试验中，各试样的损伤演化模式相近，使得其损伤演化表现相近.均起始于smin≈-2.3，即接近无损伤状态，且最终融合为一趋同水平，smax≈-1.3，即对应于单轴拉伸至塑性断裂的同一结果.

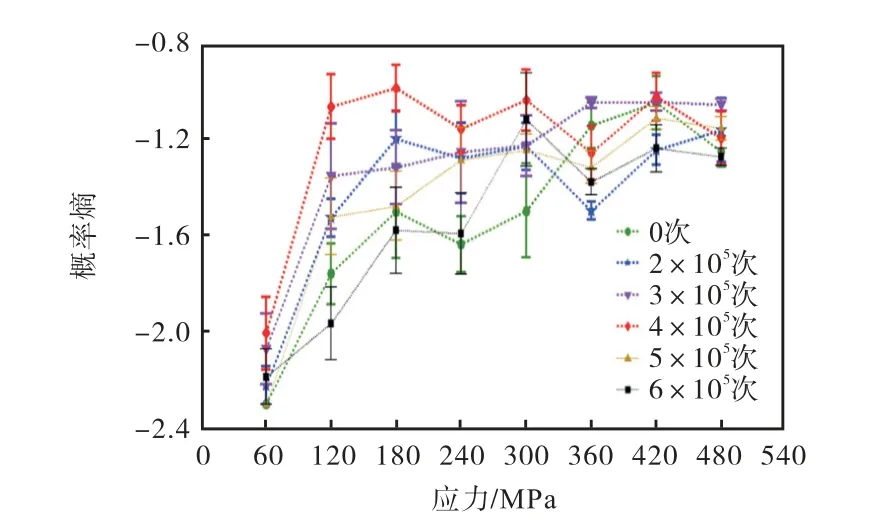
图8 不同实验条件下损伤状态轨迹曲线对比Fig.8 Comparison of the trajectory of damage state curves under different experimental conditions

进一步分析图8 曲线，并结合SEM 观测结果，有如下结论：

(1)对比各试验组损伤状态轨迹曲线，随历经疲劳循环周次的增加，0～4×105次循环试样曲线有着明显的逐渐升高，特别在60～120 MPa 阶段，呈现较为规律的上升.参考整周期疲劳试验所得批次试样在疲劳实验条件下的寿命更多集中在7×105～9×105次，表明在历经较少疲劳循环周次情况下，材料的性能退化虽不剧烈，但损伤分布相对均匀.所累积的疲劳损伤会对材料在单轴拉伸试验中的损伤演化过程产生较为明显的影响，表现为材料内部微孔穴数量变化及尺寸演化的严重程度上.对应于随机损伤事件发生概率的逐渐变化，使得各组间损伤状态轨迹曲线有着较为规律的分布.

(2)对于5×105及6×105次循环试样损伤状态轨迹曲线的相对降低，随着试样历经疲劳循环周次增至整疲劳寿命的中后期，材料内部损伤量已累积至一个较高的水平，其分布状态趋于局部集中，使得性能退化相对加剧.此时进行拉伸加载，已有疲劳损伤将促进弱化后的材料状态更早进入进一步的局部微孔穴聚结损伤演化阶段，即发生更严重损伤事件概率的升高.上述图4 所示材料微裂纹图像，是材料损伤演化过程中大尺寸微孔穴聚结为微裂纹行为的一个有力证据，也代表着此时材料性能的进一步弱化.作为5×105～6×105次循环试样拉伸试验中更为显著的损伤形式，材料内部随机损伤事件发生概率的相对降低，在损伤状态轨迹曲线上相应表现为概率熵值相对降低，亦使其损伤状态轨迹曲线整体有所降低.对此，取图8 多组损伤状态轨迹曲线分别在120 MPa、80 MPa 应力水平对应概率熵值，并辅以光滑曲线拟合.如图9 所示，其熵值变化趋势符合材料疲劳过程中其内部损伤演化不确定性的变化过程，即随历经疲劳周次的增加，损伤概率熵显示出“先上升后下降”的趋势.可以看到在熵值变化过程“转折点”处所对应的循环次数，恰好接近于材料整疲劳寿命的中后期(裂纹萌生与累积损伤形式转化等行为).

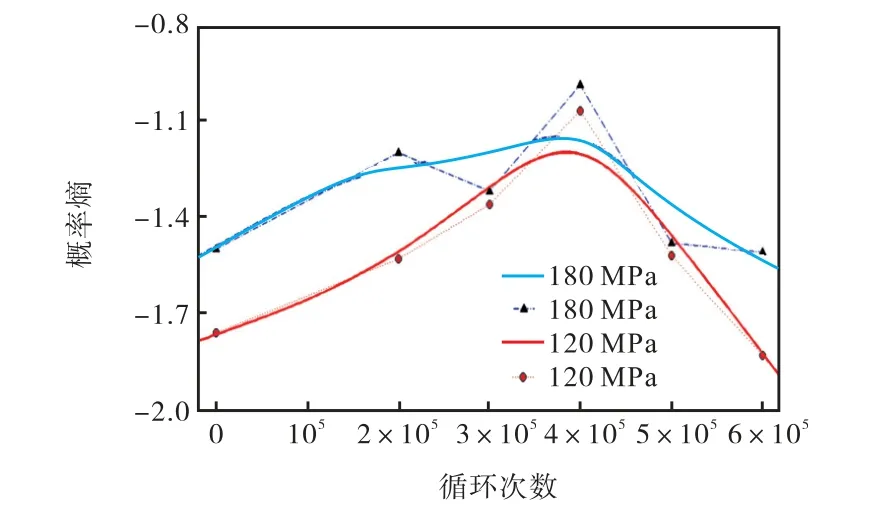
图9 概率熵值-循环周次拟合曲线Fig.9 Fitted curves of probabilistic entropy-fatigue cycles

3 结 论

(1)低碳钢材料经疲劳循环载荷后，其微观结构和宏观性能的改变可以利用拉伸试验结合声发射试验检测到.通过对AE 信号数据的统计分析，并在此基础上通过计算统计分布的概率熵，可以实现对材料损伤特性的定量表述.

(2)对不同循环次数下试样损伤状态轨迹曲线的形状和位置比较发现，其基本形状与走势相近，但在0～4×105次区间，随着循环次数的增加，对应的概率熵曲线位置呈现逐渐上升的趋势，而对于超过5×105循环的概率熵曲线，其位置又呈现下降的趋势.

(3)不同循环次数下试样概率熵曲线的位置差异和所展现的变化规律提示，本文所述试验方法和数据分析方法有望进一步用于金属材料疲劳损伤检测和寿命预测.