基于灰色关联度分析法的合金成本最优化

常锦才，马义茹，李菁月，李纯良

(1.华北理工大学 理学院，河北 唐山 063210；2.华北理工大学 3D建模与应用创新实验室，河北 唐山 063210)

0 引言

随着钢铁行业中高附加值钢种产量不断提高,如何通过历史数据对脱氧合金化环节建立数学模型，在线预测并优化投入合金的种类及数量，在保证钢水质量的同时最大限度地降低合金钢的生产成本，是各大钢铁产业提高竞争力所要解决的重要问题。现已形成了具备以合金收得率预测及成本优化算法为主体的自动配料模型，但国内钢铁企业只有部分车间引进了该项技术，而未采用该项技术的车间需要按照不同元素的固定收得率或经验计算各种合金加入量,难以实现配料的自动优化和成本控制。因此，需要通过建立模型来预测各种元素的收得率及各种合金的加入量，进而实现在尽可能提高准确率的情况下来降低脱氧合金化的成本。

由于现已有大量数据，所以可以根据灰色关联度分析法对收得率的影响因素进行分析，运用多变量曲线拟合对收得率进行预测，接着通过准则对预测收得率的准确性进行检验，最后可以使用linprog函数进行线性规划，从而得出合金配料方案以及最低成本。图1所示为降低脱氧合金化成本流程图。

图1 解决问题流程图

1 数据预处理

1.1 对异常值进行剔除

(1)连铸正样N_val、连铸正样O_val、连铸正样B_val、连铸正样Nb_val等大量的数据都为NULL，所以剔除整列数据。

(2)在所给数据中，有8种钢号，其中部分钢号所给数据偏少，用于计算结果很难趋近稳定，所以筛选出钢号为HRB400B的数据用于计算。

(3)转炉终点Si的数据中含有负数，不符合逻辑，所以剔除含负数的行。

(4)在所给数据中有少量温度数据为0，温度数据相对来说较为集中，所以可以删除为0的数据，不会造成太大影响。

1.2 对不完备数据进行处理

处理不完备数据集[1]的方法主要有三大类：

(1)删除元组：将存在遗漏信息属性值的对象删除，从而得到一个完备的信息表。当每个属性空值的百分比变化很大时，它的性能非常差，可能导致数据发生偏离，从而引出错误的结论。

(2)数据补齐：这类方法是用一定的值去填充空值，从而使信息完备化。可以用其余属性的平均值来进行补充等。

(3)不处理。

在所给数据中，缺失大量转炉终点Mn、P的数据，若使用删除元祖的处理方法势必会导致数据发生较大偏差，从而造成错误的结论。

为尽可能提高准确性，面对较为复杂的数据缺失，可以用平均值进行填充。

表1 不完备数据补充

2 C、Mn元素收得率的计算

在实际工艺流程中，钢水的脱氧合金化过程主要关注C、Mn、S、P和Si 5种元素的含量。元素收得率是指脱氧合金化的过程中被钢水吸收的元素的重量与加入该元素总重量之比。

所以元素收得率模型为：

(1)

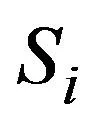
根据模型可以分别计算出如图2、图3所示C、Mn2种元素的收得率。

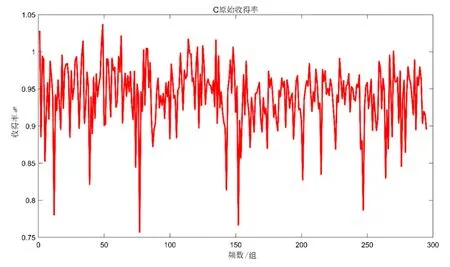
图2 C的历史收得率

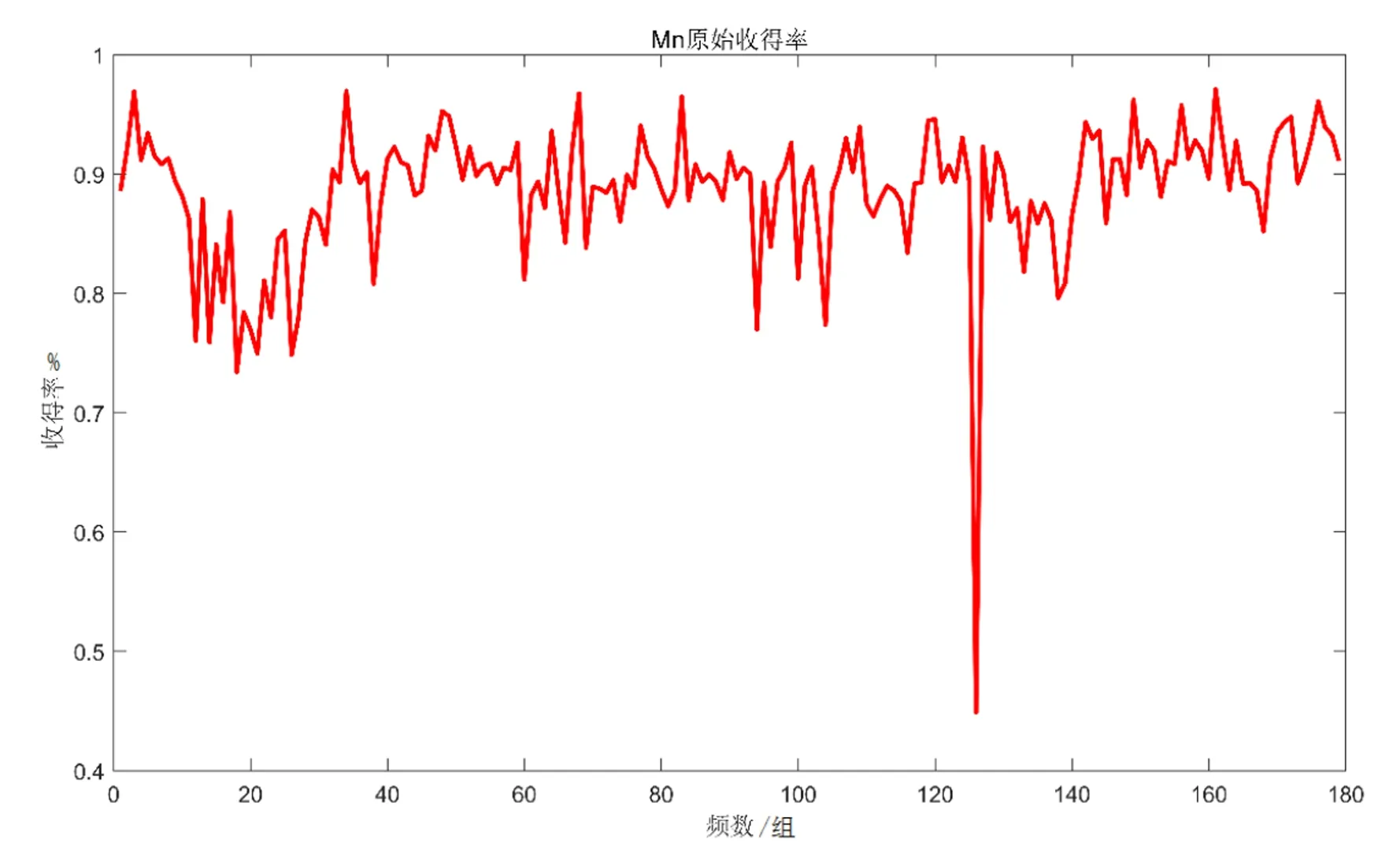
图3 Mn的历史收得率

元素收得率的范围应该在(0，1)之间，在数据处理的时候，原始数据通常都是有很多的噪点的，很多时候都会不稳定，有明显波动，所以需要对计算出的收得率进行去噪。

C元素和Mn元素收得率的分布如图4、图5所示。

图4 去噪后C的收得率

图5 去噪后Mn的收得率

去噪后C、Mn的收得率均在(0.8,1)之间，符合炼钢过程的实际情况。

3 收得率的主要影响因素

运用灰色关联度分析[2]的方法来分析主要影响因素。

灰色关联度分析法是一种多因素统计分析方法，它是以各因素的样本数据为依据运用灰色关联度来描述因素间关系的强弱、大小和次序，若样本数据反映出的两因素变化的态势(方向、大小和速度等)基本一致，则它们之间的关联度较大；反之，关联度较小[3]。

灰色关联度分析方法的步骤：

(1)根据分析目的确定分析指标体系，收集分析数据。

设n个数据序列形成如下矩阵：

(2)

(2)确定参考数据列，记作：

(3)

(3)对指标数据进行无量纲化。

采用均值化法作为无量纲化的方法，该方法在消除量纲和数量级影响的同时，保留了各变量取值差异程度上的信息。

(4)

无量纲化后的数据序列形成如下矩阵：

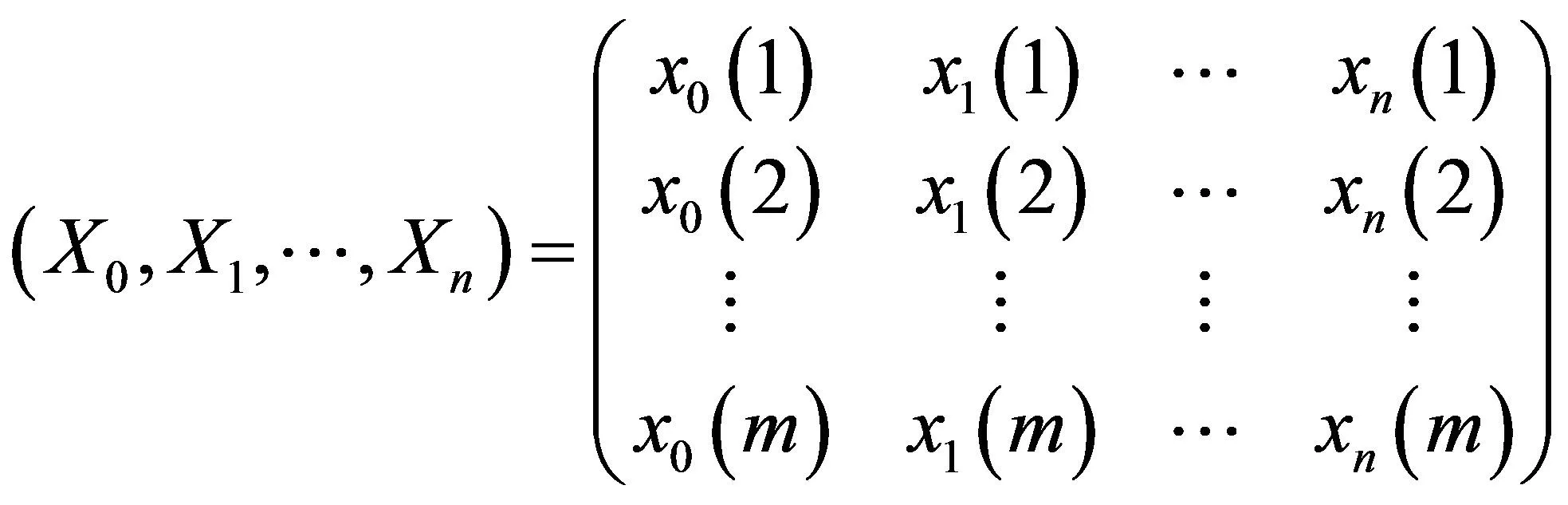
(5)

(4)逐个计算每个被评价对象指标序列(比较序列)与参考序列对应元素的绝对差值。

(6)

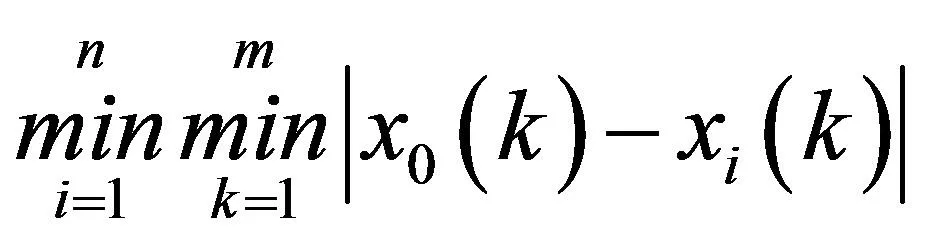
(7)

(6)计算关联序

对各评价对象(比较序列)分别计算每个指标与参考序列对应元素的关联系数的均值，以反映各评价对象与参考序列的关联关系，并称其为关联序，记为：

(8)

(7)如果各指标在综合评价中所起的作用不同，可对关联系数求加权平均值即

(9)

(8)C、Mn元素收得率的主要影响因素

依据各观察对象的关联序，得出分析结果。

C收得率影响因素降序排列：钢水净重、转炉终点温度、碳化硅、锰硅合金、转炉终点S、石油焦增碳剂、转炉终点Mn、转炉终点C。

Mn收得率影响因素降序排列：转炉终点温度、锰硅合金、钢水净重、转炉终点S、石油焦增碳剂、转炉终点Mn、转炉终点C、碳化硅、转炉终点P、转炉终点Si。

4 C、Mn收得率的预测

4.1 C的收得率预测

把影响收得率的主要因素提取出来。令C的历史收得率为因变量，收得率影响因素为自变量，对数据使用多变量曲线拟合[4]，得到收得率影响因素系数，如表2所示。

表2 C收得率影响因素系数表

由表2可知，C的预测收得率公式为：

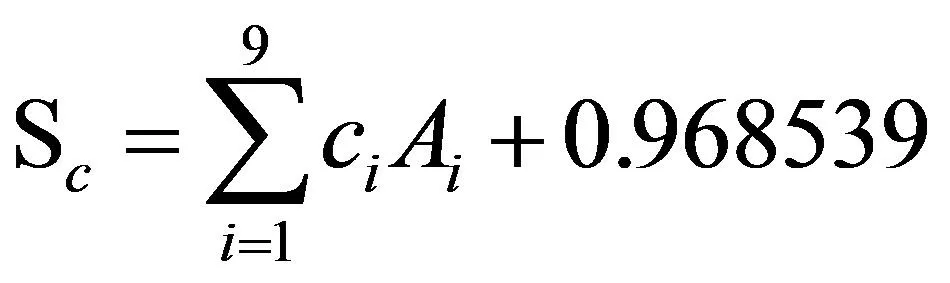
(10)

4.2 Mn的收得率预测

令Mn的收得率为因变量，收得率影响因素为自变量，对数据进行多变量线性拟合[5]，得：

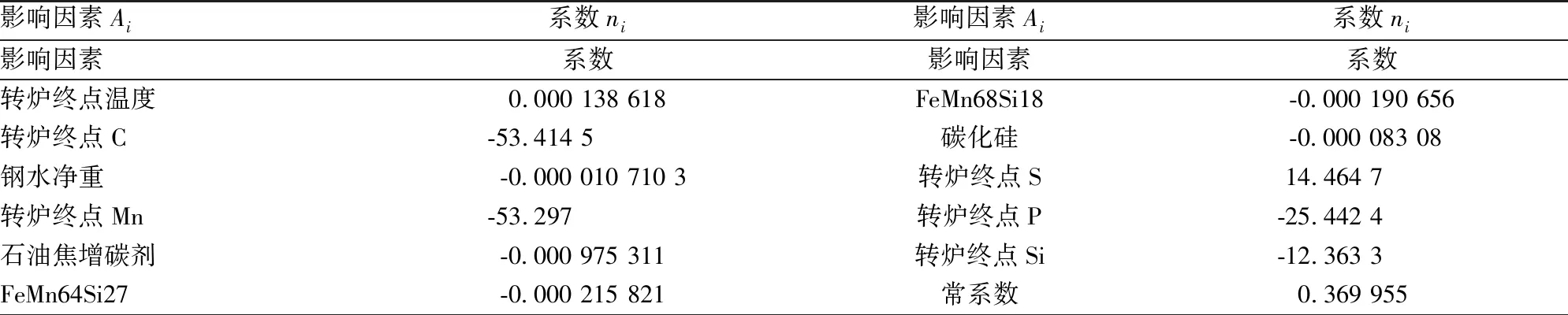
表3 Mn收得率影响因素系数表

由表3知Mn的预测收得率公式为：

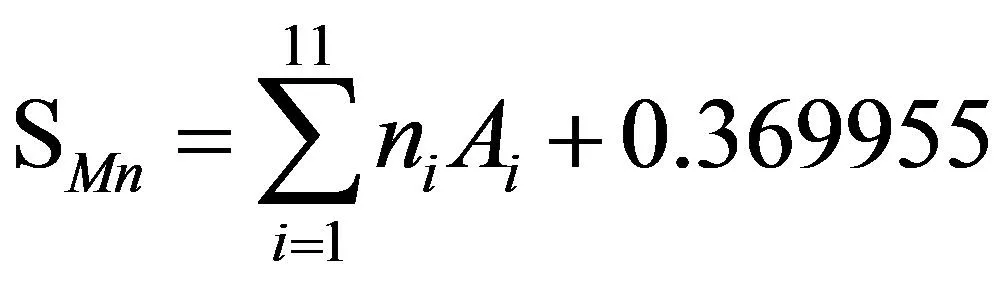
(11)

5 收得率预测准确率分析

根据预测出的元素收得率，求出对应连铸正样，公式如下[6]：

(12)

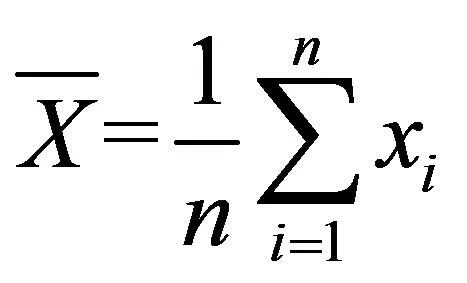
(13)

联合密度函数：

(14)

求对数函数

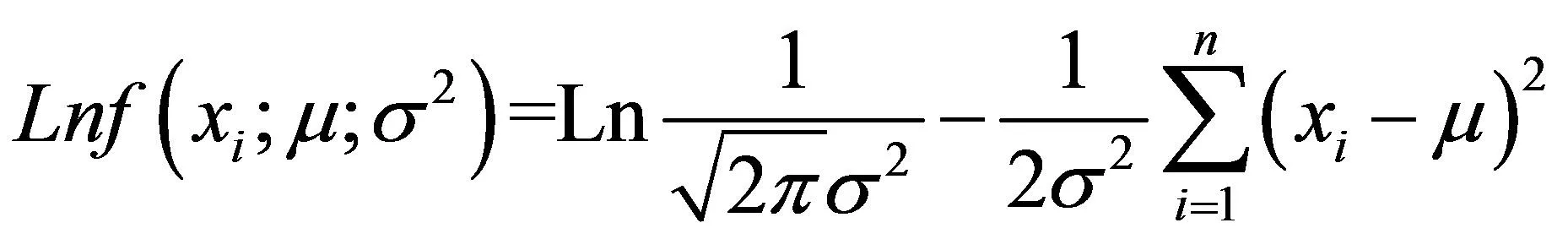
(15)

求解方程组：

(16)

解得：

(17)

由此可得出C、Mn、S、P和Si元素的正态分布函数如图6、图7所示。

图6 C元素正态分布函数

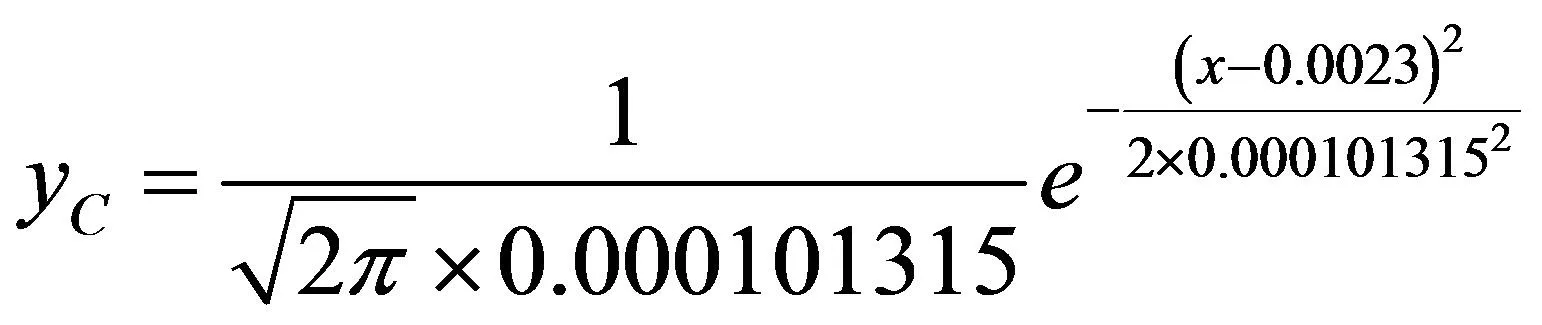
(18)

图7 Mn元素正态分布函数

(19)

根据3σ准则，求出连铸正样的区间：

3σ准则是先假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按照一定概率确定一个区间，认为凡超过这个区间的误差，就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除。且3σ准则适用于具有较多组数据的情形[8]。

根据炼钢实际情况，连铸正样应该呈正态分布，所以计算出的连铸正样预测收得率若落在3σ区间内，则预测是准确的。

经统计计算，C的预测收得率准确率为0.989 830 508；Mn的预测收得率准确率为0.989 270 386。

6 合金配料方案优化

要实现钢水脱氧合金化成本优化[9]计算，根据表中合金元素含量及合金收得率预测各种合金的所需用量。要在保证钢水质量的同时最大限度地降低合金钢的生产成本，也就是合金化成本优化计算。同时，要给出合金配料方案[10]。已知合金配料价格如表6所示。

表6 合金配料价格

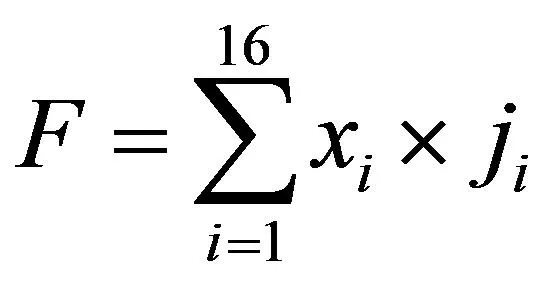
第2步：找出线性约束条件。

方法一：以主要元素含量的国家标准作为约束条件[12]，表7所示为主要元素含量国家标准。

表7 元素含量国家标准

其中C、Mn、S、P、Si内控区间的上下限分别作为约束条件，为了使计算简便，由收得率的公式逆推出如下公式：

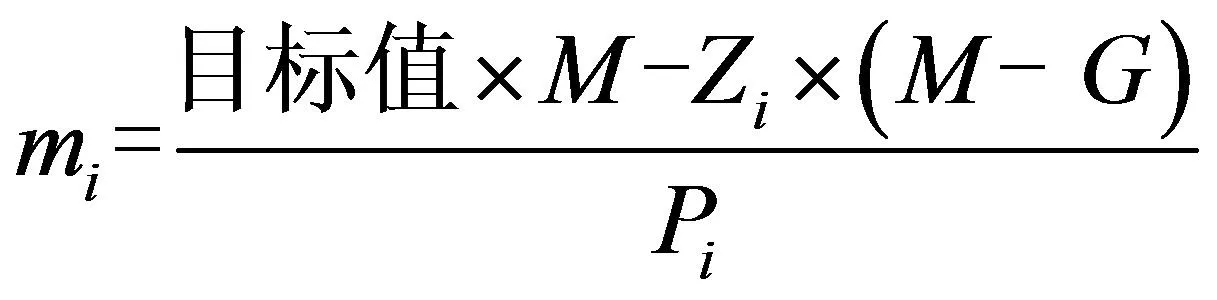
(20)

其中目标值即分别代入约束条件对应的值，从而得到如下新的约束条件[13]，

C含量的约束条件如式(21)：

(21)

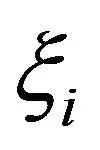
Mn含量的约束条件如下：

(22)

S含量的约束条件如下：(实际S的收得率为1)

(23)

P含量的约束条件如下：(实际P的收得率为1)

(24)

Si含量的约束条件如下：(实际Si的收得率为1)

(25)

各种合金用量总质量小于钢水净重：

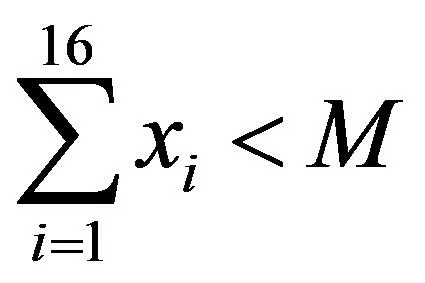
(26)

各种合金质量大于等于0：

(27)

方法二：

表8 3σ区间

C含量的约束条件如下：

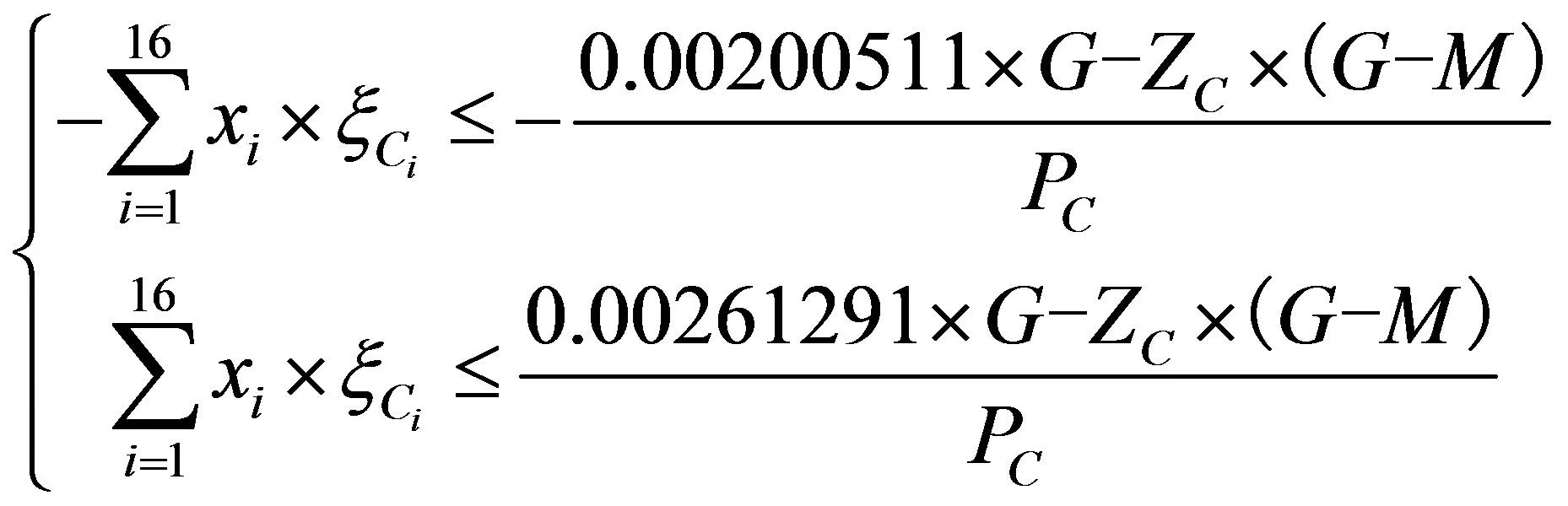
(28)

Mn含量的约束条件如下：

(29)

S含量的约束条件如下：(实际S的收得率为1)

(30)

P含量的约束条件如下：(实际P的收得率为1)

(31)

Si含量的约束条件如下：(实际Si的收得率为1)

(32)

各种合金用量总质量小于钢水净重：

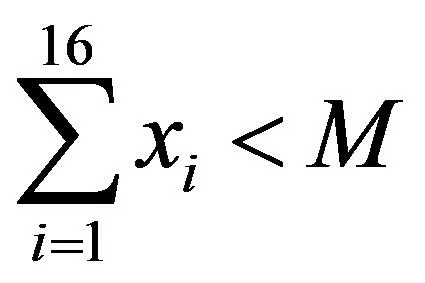
(33)

各种合金质量大于等于0：

(34)

第3步：建立数学模型，进行线性规划。

利用linprog函数进行线性规划。linprog函数如下：

[x,Fval]=linprog(c,A,b,Aeq,beq,lb,ub,x0)

(35)

根据以上2种方法得出合金配料方案对比如表9所示[15]。

表9 合金配料方案

由表9可知,方法一得出的合金最优配料方案为：一吨成品钢需要硅铝锰合金球用料1.525 4 t，硅铁FeSi75-B用料0.118 0 t，最低成本为12 136元。

方法二得出的合金最优配料方案为：一吨成品钢需要硅铝锰合金球用料1.660 6 t，硅铁FeSi75-B用料0.116 8 t，最低成本13 158元。

7 结论

(1)应用灰色关联度分析方法，得出影响元素收得率的主要因素，运用多变量曲线拟合得到收得率预测公式。利用准则对其进行准确率的鉴别，准确率高达98%以上，肯定了收得率预测的准确性。

(2)使用函数，分别以准则和合金元素国家标准区间作为约束条件，进行线性回归，得出合金成本最低的配料方案。结果表明该方案可以通过建立模型来预测元素的收得率及合金的加入量，进而在提高预测准确率的情况下来降低脱氧合金化成本。