Fe-0.3C-6Mn中锰钢热变形行为及热加工图研究

陈连生，闫博伟，李红斌，2，田亚强，刘倩

(1.华北理工大学 冶金与能源学院，河北 唐山 063210；2.华北理工大学教育部现代冶金技术重点实验室，河北 唐山 063210)

0 引言

随着全球能源与环境问题日益严峻，汽车制造正向着减轻自重的方向发展，用以满足节能减排和安全环保的要求[1]。作为第3代先进高强钢中最具代表的中锰钢，可以很好地满足安全与环保的要求。目前，对中锰钢的研究主要集中在热处理过程中的微观组织及之后的力学性能等方面[2-5]，而在热加工过程中，材料内部会发生复杂的物理化学反应如回复，再结晶，第二相析出等。此外，一些研究表明，奥氏体晶粒尺寸大小会影响到奥氏体的稳定性[6]以及奥氏体向马氏体转变产物的结构[7]；显然奥氏体稳定性以及马氏体转变类型会对中锰钢后续热处理过程的组织调控产生影响，因此有必要对中锰钢的热加工行为展开研究。孙国宁[8]利用Sellars提出的模型构建了Al-Mn-Er-Zr合金的高温本构方程，计算结果表明，应力实测值与计算值误差在6%以内，可以很好地反应高温流变行为。此外，热加工图也是一种有效的辅助技术，可用于热加工参数的设计与优化[9]。蔡薇[10]通过高温等温压缩实验，绘制了Cu-Cr-Zr-Ti合金的热加工图，得到了此合金最佳的热加工参数是变形温度为900 ℃，应变速率为0.01 s-1。热加工图可以表明失稳状态与变形条件之间的关系，从而获得材料的最佳热加工窗口。但是这些分析都是基于压缩过程中的流变曲线，但是在压缩过程中，由于工件端部与压头之间会产生摩擦，这必然会对所得的曲线产生影响。

该研究采用单道次热压缩试验，研究了中锰钢的流变行为，并通过摩擦修正方法对流变曲线进行摩擦修正，根据摩擦因素修正后得到的流变曲线建立了相应的应力-应变曲线本构方程和热加工图，结合实验微观结构，分析了微观结构演化与变形条件之间的关系，该研究旨在分析中锰钢的热变形行为，并预测出材料的最佳的热加工工艺参数。

1 试验材料及方法

采用真空感应炉冶炼浇铸了50 kg的微合金化中锰钢钢锭，其化学成分如表1所示。经成分均匀化后，加工成φ8 mm×12 mm的圆柱体，在Gleeble3500热模拟试验机上进行压缩试验，变形温度为900 ℃、950 ℃、1 000 ℃、1 050 ℃、1 100 ℃和1 150 ℃；应变速率分别为0.01 s-1、0.1s-1、1s-1和10 s-1。实验流程如图1所示，表1 所示为实验材料的化学成分。

图1 实验流程示意图

表1 实验材料的化学成分(质量分数，%)

2 本构方程的建立

2.1 流变曲线的摩擦修正

试样在塑性加工过程中，压头与试样之间会产生相对滑动的趋势，因此，在压缩过程中，会产生摩擦行为，摩擦的产生会进一步影响试样在压缩过程中的流动行为，变形前后的示意图，如图2所示。

图2 试样压缩示意图

该项研究采用Li[11]的方法对流变曲线进行摩擦修正，其修正结果与实际所得结果进行对比，如图3所示。

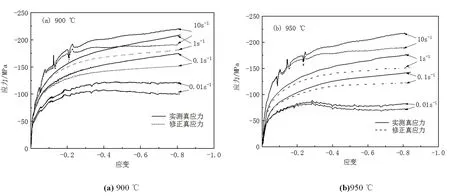
图3 实测应力与改进摩擦修正应力对比

由图3中实测真应力与修正真应力对比可知，随着试验过程的进行，摩擦对所得曲线的影响越来越大，通过修正摩擦减小摩擦对实验结果产生的影响，随着应变速率的提升，每组曲线中的偏差程度也就越大，与传统的方式[12]相比，更加切合实际。

2.2 本构方程的建立

(1)

(2)

(3)

σ——流变应力/MPa；

Q——应变激活能/Kj·mol-1；

R——气体常数/J ·(mol· K)-1；

T——绝对温度/K；

σ0——指定应变下应力/MPa。

Z因子可以表示为：

(4)

对式(1)和式(2)取对数可得：

(5)

(6)

图4 应力与应变速率关系

对式(3)取对数并进行求导可以得出：

(7)

(8)

图5 ln[sinh(aσ)]-T与 ln[sinh(aσ)]-的曲线

对式(4)取对数可得：

lnZ=lnA+nln[sinh(aσ)]

(9)

将相应参数的值带入式(9)中，得到lnZ-ln[sinh(aσ)]ln[sinh(aσ)]的关系曲线如图6所示。

图6 lnZ- ln[sinh(aσ)]关系曲线

由图6可知，lnA=20.41，即A=4.81×1 013。

根据Lin[13]的构建本构方程方法，利用修正摩擦因素后得到的流变曲线数据，构建本构方程参数，4个参数与应变ε之间的关系如图7所示。

根据图7，对数据进行拟合，得到参数与应变之间的关系以及本构方程：

Q=385.176 78+248.983 1ε+1 180.9311ε2+2 615.616 99ε3+2 108.400 91ε4-858.121 15ε5-1 451.292 47ε6

a=0.012 93-0.054 84ε+0.178 48ε2-0.243 72ε3+0.118 37ε4

n=15.904 04-63.322 07ε+232.101 63ε2-350.046 34ε3+181.409 52ε4

A=7.136 12×1013+2.723 689×1014ε+9.112 147×1014ε2-1.702 54×1014ε3-6.561 747 5×1015ε4

-1.220 017 46×1016ε5-6.808 393 5×1015ε6

(10)

图7 参数Q、a、n、A随应变变化曲线

3 热加工图的绘制与分析

热加工图由功率耗散图与流变失稳图组成。依据热加工图技术可以分析试验钢在不同变形条件下的热变形行为，从而获得热加工过程中的优良加工区域和不适于加工区域，从而达到控制组织演变、避免缺陷产生和优化工艺参数的目的[14]。

3.1 功率耗散图的绘制

根据动态材料学模型[15-20]的观点，材料的成型过程可视为材料本身能量耗散的过程。消耗的能量包括成型过程所需的能量和成型过程中微观演变需要的能量。其中微观演变所需能量与总的消耗能量相比之值就是功率耗散因子的值，功率耗散因子可由式(11)求出。

(11)

在成型过程中，当微观演变所需要的能量越接近总体消耗的能量时，也就是上式中分子越接近分母时，功率耗散因子的数值也就越大，这就意味着材料的动态再结晶发生的越完全。

3.2 流变失稳图的绘制

(12)

式中a、b、c、d——多项式的系数。

材料的失稳判据为式 (13) 所示，将式 (12) 所求的4个参数值代入式(13)中，即可得到流变失稳参数。

(13)

3.3 热加工图

将绘制成阴影的流变失稳区域，叠加在功率耗散图上，即为所得热加工图，如图8所示，为不同应变下的热加工图。

图8 不同应变下热加工图

由图8可知，随着真应变的增大，最大的功率耗散因子值均出现在1 050～1 150 ℃、应变速率在0.01～0.05 s-1区间内，功率耗散因子的值介于0.36～0.55之间。根据文献[22，23]功率耗散因子值大的区域对应为动态再结晶。在功率耗散因子值大的区域内，材料的流动应力随真应变的增大而减小，材料发生软化。因此，由该区域的微观演变机制结合图9可知，材料发生动态再结晶。而热加工图上的流变失稳区在900～1 000 ℃时，随着真应变的增加逐渐向高应变速率处发生了移动，而在真应变0.5～0.8，1 050～1 150 ℃区域时，流变失稳区逐渐向低应变速率处发生移动。综上所述，材料最佳的热加工区间在1 050～1 150℃、应变速率在0.01～0.05 s-1区间内。

图9 再结晶区域与失稳区域组织图

由图9(a)、图9(b)可知，在1 150 ℃、0.01～0.1 s-1区域内，材料的微观结构为再结晶组织结构，晶粒形状多为多边形形状，具有良好的加工性能，随着应变速率增加，变形时间缩短，再结晶晶粒的尺寸逐渐减小。此外，由图9(c)、图9(d)可知，在变形温度为900 ℃，应变速率为10 s-1和变形温度为950 ℃，应变速率为1 s-1的失稳区域内，材料内部组织结构中一小部分发生了动态再结晶，大部分组织结构为不规则形状或被拉长的晶粒，合金处于不稳定状态，在低温高应变速率条件变形下，短时间内动态再结晶发生不充分，塑性变形过程的进行引起位错密度增加，位错密度增加之后使得不同方位上位错堆积缠结，致使位错的运动受到不同方位上位错的阻碍，从而使得加工硬化非常明显，所以该加工区域为失稳区域，材料内部混晶严重，在随后的相变过程中，粗大的奥氏体晶粒会转变成粗大的马氏体，往往超过常规的马氏体要求[24]。在加工过程中，当受力不均匀时在粗细晶交界处或粗晶内首先形成裂纹，所以失稳区域不可应用于加工。

4 结论

(1)得到材料的应变激活能Q的范围为363～375Kjmol-1，并构建了基于双曲正弦函数的全应变本构方程。

(2)根据热加工图计算结果表明，温度在1 050～1 150 ℃、应变速率在0.01～0.05 s-1时可以获得较为细小的奥氏体晶粒。并通过对相应参数下的奥氏体晶粒进行金相检验，验证了预测结果的准确性。

(3)由微观组织分析可知，在预测的实验参数条件下，组织为再结晶组织，而在失稳参数下，组织为细小晶粒与变形后形成的条状晶粒形成的混晶组织，在加工过程中，当受力不均匀时在粗细晶交界处或粗晶内首先形成裂纹，所以失稳区域不可应用于加工。