主元法巧解导数压轴题*

苏艺伟 张兵源

(福建省龙海第一中学新校区，363100) (福建省漳州市教育科学研究院，363000)

许多数学问题中都含有常量、参量、变量等多个量.通常情况下，有一些元素处于突出和主导的地位，可视之为主元.在某些情况下，为解决问题的需要，我们也可人为突出某个元素的地位作用，将之当作主元.确立主元后，以此作为解题的主线进而把握问题，促使问题转化直至问题解决的思想方法称为主元法.数学中的多元参数问题，若按常规思路确定主元，可能导致问题复杂化，此时，若能针对题目的结构特征，改变思考的角度，重新选择某参变量为主元，另辟蹊径，往往可以使问题化难为易，迅速求解.在导数试题中，经常涉及到多个变量(如x、a、b等)，解题常规思路是以x为主元求解.但是对于不少导数压轴试题，以x为主元进行求解会十分繁琐.此时如果能够改变思路，重新确定主元，则会使得解题过程格外简捷自然.

例1已知函数

(1)若x=x0时，f(x)取得极小值f(x0)求a及f(x0)的取值范围；

(2)当a=π，00.

解(1)略.

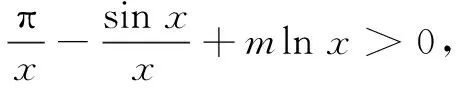
当x=1时，h(m)=π-1>0.

综上，h(m)>0，即f(x)+mlnx>0.

评注如果以x为主元求解问题(2)较为繁琐.此时重新确定m为主元，要证h(m)>0，只需对lnx进行分类讨论即可，这使得解题过程大大简化.

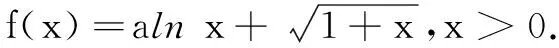
解(1)略.

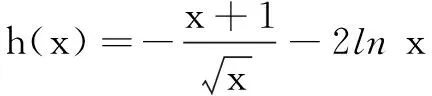
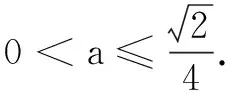
例4已知函数f(x)=ex-x，g(x)=(x+k)ln(x+k)-x.对任意的a、b>0，不等式f(a)+g(b)≥f(0)+g(0)+ab恒成立，求正实数k的取值范围.

解由已知，可得ea-a+(b+k)ln(b+k)-b-1-klnk-ab≥0，a>0,b>0,k>0.

记h(a)=ea-a+(b+k)ln(b+k)-b-1-klnk-ab，则h(a)≥0.

h′(a)=ea-1-b，令h′(a)=0，得a=ln(b+1).易知h(a)在(0,ln(b+1))单调减，在(ln(b+1),+∞)单调增，故h(a)≥h(ln(b+1))，即h(a)≥(b+k)ln(b+k)-(b+1)ln(b+1)-klnk.

记t(b)=(b+k)ln(b+k)-(b+1)ln(b+1)-klnk，则t′(b)=ln(b+k)-ln(b+1).

若k≥1，则t′(b)≥0，t(b)在(0,+∞)单调增，t(b)>t(0)=0,此时h(a)>0，符合题意.

若0

综上，可得k≥1.

评注本题通过两次重新确定主元，将复杂的多元问题转化成简单的问题，提高了解题效率.

不难发现，对于此类导数试题，当面对题目中含参数问题时，若以x为主元证明很困难，可通过重新确立主元的方法，往往会化繁为简，化难为易，化抽象为具体，使求解过程更加简捷.