一种基于窄带自相关的实信号频率估计算法

曹 燕， 王一歌， 李欣雯， 赵明剑， 丁泉龙

(华南理工大学电子与信息学院，广州 510641)

正弦信号分为复正弦信号和实正弦信号。实正弦信号在频域中除了含有正频率外，还有“负频率”[1]，会在一定程度上造成频谱的混叠，因此其频率估计比复正弦信号复杂。在实际工程应用中，涉及的信号多数为被高斯白噪声污染的实正弦信号，由于不能直接应用复正弦信号的相关方法，因此如何从混有高斯白噪声的实信号样点中提取信号的频率一直以来都备受关注。

正弦信号的频率估计有基于时域特性和基于变换域特征的两种方法。基于时域的方法相对简单，特别是利用少量的点在实时计算上有优势[2]。基于变换域的频率估计方法通常是考虑信号的频域特性，在估计性能上有一定的优势，但实现较为复杂。由于正弦信号的自相关仍然是同频率的正弦信号，且去除部分噪声影响，所以，在时域中基于自相关的频率估计算法颇多，例如Pisarenko谐波分解(pisarenko harmonic decomposer，PHD)[3]算法，改进协方差(modified covariance，MC)[4]算法、以及基于自相关的一些改进频率算法[5-10]，如利用更多的自相关系数[8]或是多步自相关[9-10]来提升估计性能。文献[4]把MC运用到自相关序列，提出了基于自相关线性预测误差最小的估计器。

基于频域的频率估计方法一般先进行频率粗估计，再进行频率细化。粗估计是寻找幅度谱的谱峰，可利用(快速傅里叶变换,fast fourier transform,FFT)实现，但是会出现 “栅栏”效应[11]，导致频率估计精度降低。为了提高精度，可对原始序列补零后再做FFT。频率细化的一种方法是基于插值的方法[12-16]。Quinn[12]提出利用最大谱峰和相邻次大谱峰对应的傅里叶系数进行插值来实现复正弦信号的频率估计。文献[15]在不对原始实信号补零的情况下，利用最大谱峰和相邻次大谱峰三点来内插，得到频率的精估计。

现结合时域和频域自相关的特点，提出一种基于窄带自相关的实信号频率估计算法。该算法在频域进行谱峰搜索后，利用信号的窄带功率谱来计算自相关，以消除窄带外的噪声对频率估计的影响，然后再用简单的时域自相关的MC算法来得到频率估计的闭式解。最后给出与时域自相关MC算法，以及频域全频带的自相关MC算法和频域三点内插算法[15]相比较的仿真结果。

1 基于自相关的实信号频率估计

1.1 实信号的自相关函数

假设原实正弦信号为

s(n)=acos(ω0n+φ)，n=0,1,…，N-1

(1)

式(1)中：a、ω0、φ分别表示信号的振幅、频率和相位。混入噪声的信号为

x(n)=s(n)+z(n)

(2)

式(2)中：z(n)为高斯白噪声，其均值为0，方差为σ2。它的自相关函数为

(3)

式中：τ为自相关函数的下标，τ=0，1,…,N-1，有噪声情况下，实信号的自相关函数为

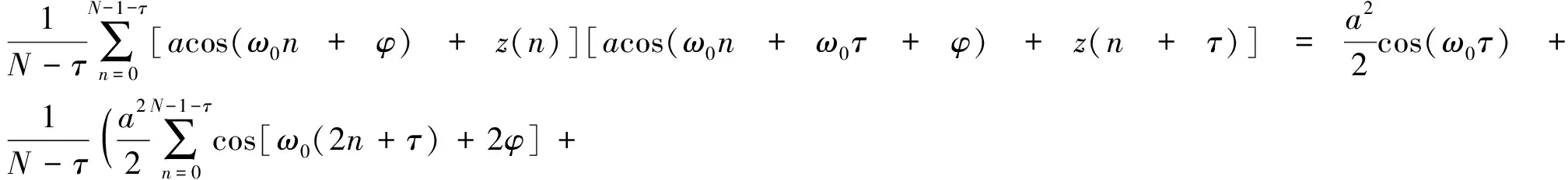
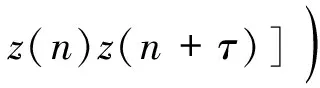
(4)

当N足够大时，自相关函数的期望为

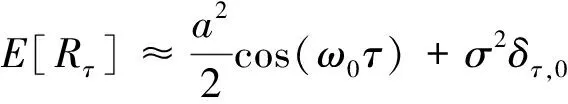
(5)

式(5)中：δτ,0为克罗内克(Kronecker)函数：

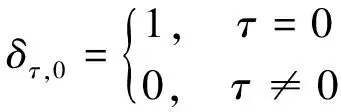
(6)

可以看出，在有噪声或者无噪声的情况下，正弦信号的自相关函数仍为与原信号同频率的正弦信号。而高斯白噪声的自相关函数的期望只有在零点位置存在，其余位置均为0。所以，利用非零序号的自相关可以估计原信号的频率，同时还可以在一定程度上降低噪声的影响。

1.2 基于原信号的MC算法

由于正弦信号s(n)具有线性预测特性：s(n)=2cosω0s(n-1)-s(n-2)，也可以时延后写成：

s(n+2)=2cosω0s(n+1)-s(n)

(7)

基于这种线性预测，对含噪的实正弦信号模型，可定义预测误差函数e(n)为

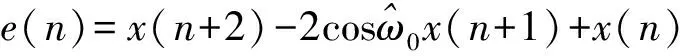
(8)

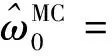
(9)

1.3 基于信号自相关的MC算法

1.3.1 基于时域自相关的MC算法

由于正弦信号的自相关函数仍为与原信号同频率的正弦信号，仍然具有线性预测特性。对照式(7)，自相关函数显然也满足：

Rτ+2≈2Rτ+1cosω0-Rτ

(10)

定义误差函数：

eτ=Rτ+Rτ+2-2cosω0Rτ+1

(11)

的和取最小值，即可以求得:

(12)

式(12)用自相关序列{Rn1,Rn1+1,…,Rn2,Rn2+1,Rn2+2}来估计信号的频率，其中n1、n2+2分别表示所需自相关系数的起始和截止下标。由式(6)可知，高斯白噪声的自相关函数的期望只有在零点位置存在，其余位置均为0，也就是说序号小的自相关系数受噪声的影响会大于序号大的自相关系数，但是从自相关的定义式(3)来看，当信号的长度N一定时，随着自相关系数序号的增大，所用的信号变少，求和数变少，又会影响自相关本身定义的准确性，因此n1取值也不能太大。当自相关序列直接从时域，即从式(3)来求解时，该算法称为时域自相关的MC算法。

1.3.2 基于频域全频带自相关的MC算法

根据Weiner-Khintchine定理，信号的功率谱和其自相关函数服从一对傅里叶变换关系，自相关函数可以看成功率谱的傅里叶反变换，即：

(13)

2 基于频域窄带自相关的MC算法

2.1 算法思想

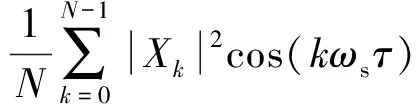
(14)

(15)

式(15)中：Δ为窄带的前后宽度，表示选取谱线的范围。式(15)和式(14)相比，限制了窄带外的噪声对频率估计的影响，同时带来计算量的减少。将式(15)代入式(12)，即可得到本文算法的频率估计表达式：

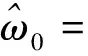
(16)

此算法只用了窄带里面的谱线，因此称为频域窄带自相关的MC算法。

2.2 算法流程及计算量分析

该算法的实现流程如下：

该算法只用一次FFT，由于用的谱线少，式(15)的求和计算量少于IFFT的计算量，式(12)的计算量是一样的，因此可以看出计算量比频域全频带自相关的MC算法少。而式(3)计算自相关的计算量远大于FFT，故该算法与时域自相关的MC算法相比，有明显的计算优势。

3 算法仿真及性能比较

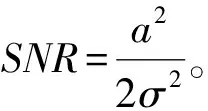
3.1 不同补零倍数的仿真

本文提出的频域窄带自相关的MC算法是基于频域进行分析，得到一个幅度谱谱峰，再通过自相关在时域的特点来进行频率估计的，因此可以补零增加信号的长度来得到更为准确的谱峰，使最后的频率估计更为精确。图1是本文算法补p-1倍零的仿真结果，以及频域全频带自相关的MC算法在p=1时候的仿真。注意p=1，表示补p-1=0倍零，即表示没有补零。可以看出，在没有补零(p=1)的时候，在低信噪比下，本文算法由于用窄带功率谱表示自相关，去除了带外的噪声，性能优于频域全频带自相关的MC算法，但是当噪声影响不大，信噪比提高之后，频域全频带自相关的MC算法由于用了全频带的信息，使得自相关系数更为准确，因而均方误差低于本文算法。一旦补零后，本文算法的性能就得以提高，SNR≥-7 dB下均方误差就达到CRB，且在随着补零倍数的增多，性能越来越好。

图1 本文算法不同p在不同信噪比下均方误差的对比Fig.1 Mse vs SNR for different p of the proposed algorithm

3.2 自相关系数不同起始的仿真

从式(16)可知，不同的n1、n2对频率估计的结果有影响，下面通过仿真来说明。图2描述本文算法在n1=2、不同n2时的均方误差比较。另外信号ω0=0.3π，SNR=20 dB，M=4N,Δ=3。为了保证自相关估计的估计精度，这里的n1=2，而n2的范围是n1+1≤n2≤N-2。从图2中可以看出本文算法在n2比较小的时候，即和n1相差不大时，所用的自相关系数比较少，性能比频域(全频带)自相关的MC算法差，但是随着n2的增大，本文算法的均方误差一直下降，当n2接近200时，其性能超过频域(全频带)自相关的MC算法，达到CRB，再增大n2，下降趋势变得比较平坦。

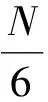
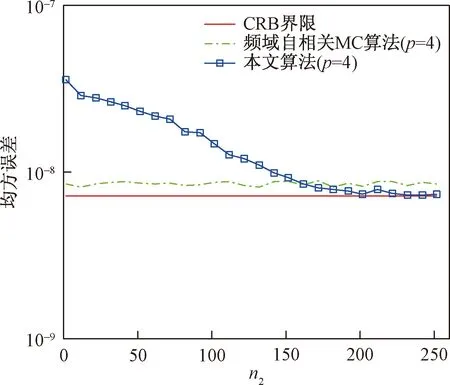
图2 本文算法在不同n2时均方误差的对比，SNR=20 dB，n1=2Fig.2 Mse vs n2 with SNR=20 dB，n1=2 for the proposed algorithm

图3 不同n1时算法均方误差的对比，SNR=20 dB，n2=254Fig.3 Mse vs n1 with SNR=20 dB，n2=254 for the proposed algorithm

图4列举了(n1,n2)={(2,256)，(2,120)，(40,120)，(40,256)，(120,256)}这几种情况下本文算法(p=4)的性能。 可以看出在SNR接近-7 dB时，这几种情况下的均方误差都能达到CRB，而频域(全频带)自相关的MC算法(p=4)只有在SNR≥18 dB后才有比较好的性能。然而随着信噪比的增大，自相关去噪的效果在减弱，反而是本身的自相关估计占据更为重要的作用，而序号比较小的比序号大的估计更为精确，同时自相关系数越多算法估计性能越好，如(n1,n2)=(2,256)；而自相关系数用的比较少的时候，算法估计性能变差，特别是用高序号自相关系数比较多，低序号自相关系数比较少时，性能变差，如(n1,n2)={(40,120)，(40,256)，(120,256)}比(n1,n2)=(2,120)差。

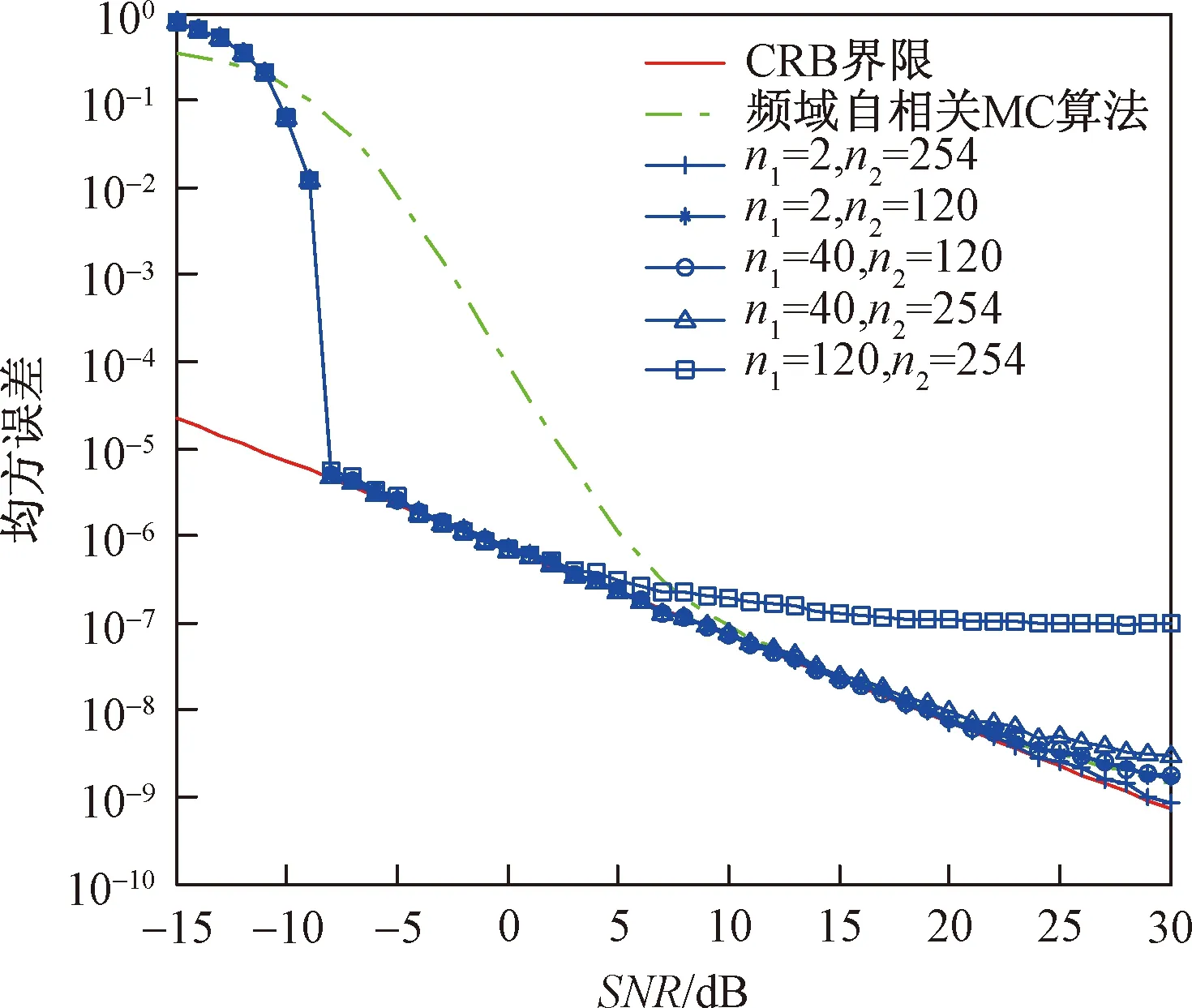
图4 不同n1,n2，本文算法在不同信噪比下的均方误差对比Fig.4 Mse vs SNR for different n1,n2 for the proposed algorithm

3.3 不同算法的性能比较

这里给出本文频域窄带自相关的MC算法与基于时域的原信号的MC算法、时域自相关的MC算法、和基于频域的频域全频带自相关的MC算法、文献[15]提出的频域三点内插算法进行比较。这里自相关的系数下标选用n1=2，n2=N-2，为了粗估计谱峰的统一，选用M=4N,Δ=3。

图5给出了不同信噪比情况下的比较，其中ω0=0.3π。可以看出本文算法在SNR≥-7 dB下均方误差达到CRB，估计器的性能远远超过基于时域的原信号的MC算法、时域自相关的MC算法；在SNR<10 dB时，性能优于基于频域的频域全频带自相关的MC算法，体现出低信噪比下去除带外噪声带来的好处；由于频域三点内插算法是基于原信号频谱的，而基于频域的频域全频带自相关的MC算法和本文算法都补取了3倍信号长度的零，因此可以看到本文算法一直都优于它，基于频域的频域全频带自相关的MC算法在SNR>5 dB后性能也超过它。

图6给出了SNR=10 dB时不同频率处的性能比较，也可以明显看到本文估计器的均方误差远远低于基于时域的原信号的MC算法、时域自相关的MC算法和基于频域的三点内插算法，在ω0∈[0.15π,0.85π]都达到CRB；在ω0∈[0.4π,0.6π]，本文算法和频域全频带自相关的MC算法有相比拟的性能，而在其他频率处都超过其性能。

图5 不同信噪比下不同算法的均方误差对比Fig.5 Mse vs SNR for different estimator

图6 不同频率ω0下不同算法的均方误差对比，SNR=10 dBFig.6 Mse vs ω0 for different estimator with SNR=10 dB

最后，图7给出了信号长度N对估计器性能的影响，同样ω0=0.3π，SNR=10 dB。可以看到随着N的增加，本文算法、时域自相关的MC算法、和基于频域的三点内插算法和频域全频带MC算法的性能得到了很大的提升，而MC估计器的性能趋于平缓。在N<150时，本文估计器的均方误差比频域全频带MC估计器低一点，且随着N的增大，这种优势也越来越明显，前者可以达到CRB，而后者逐渐远离。在不同长度下，本文算法都优于与之比较的其他算法。

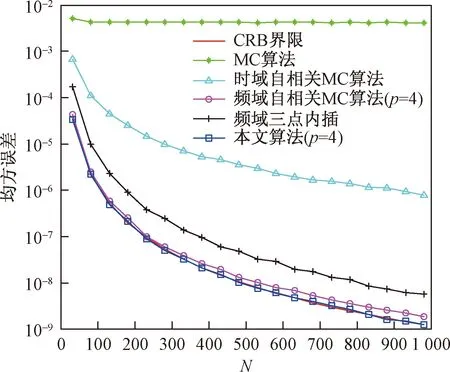
图7 不同信号长度N下不同算法的均方误差对比，SNR=10 dBFig.7 Mse vs N for different estimator with SNR=10 dB

4 结论

结合时域和频域自相关的特点，给出了一种基于窄带自相关的实信号频率估计算法，该算法通过在时域上避开选择受噪声影响比较大的低序号自相关系数，在频域上利用信号的窄带功率谱来计算自相关，去除带外的噪声，这样来提高估计器的估计性能。仿真结果也表明该算法性能优于传统的时域算法：MC算法和基于时域自相关的MC算法，以及传统的频域算法：频域全频带自相关的MC算法和频域三点内插算法，在-7 dB信噪比时就能逼近CRB界。特别是本文算法和基于时域自相关的MC算法、频域全频带自相关的MC算法相比，都是基于自相关的算法，但是在性能上和计算量上却有比较明显的优势。