基于水利水电工程质量监督数理统计学的假设检验应用研究

李玉超

(海南中南标质量科学研究院，海南 海口 570023)

为保证水利水电工程的质量，根据水利部颁发的检测管理规定对新开工的水利工程和尚未续建工程进行对比检测，以便校验工程的施工自检。具体检验项目由质检单位审定，依法治水，强化水利工程建设的质量监督，确保工程质量具有重要意义[1]。

在进行工程验收时，要以施工单位自检为验收依据，以真实可靠的施工单位自检成果为前提条件，以此保证检验施工单位自检成果的真实性。在验收前，要对比检测试样，基于数理统计学进行假设检验，对施工单位自检的实验结果和对比检测的实验结果进行统计推断。其余的试样则由施工单位自检，如果检验结果可靠，则2个样本应为同一个总体；若仅容量不同，则两者之间不存在较大的差异，且具有一致性[2]。随机样本具有随机性，不可能包含总体的全部信息，因此，2个样本之间必然存在很大的差异，此时需应用假设检验方法分析两者之间存在的差异，确保两者之间具有可比性，避免受取样时间分布和原材料变化等影响造成的误判，在对施工单位自检进行分析评价时，要判别施工单位自检成果的真实性和可靠性，实现对水利工程质量的有效监控，否则起不到预期的结果[3]。数理统计学方法科学可靠，能够对施工单位的自检成果进行有力的监督。为此，提出基于水利水电工程质量监督数理统计学的假设检验应用研究[4]。

1 假设检验应用研究方法设计

1.1 数理统计学假设检验变量选择

传统的研究方法会产生有偏的参数估计，导致有偏的预测，降低参数估计的有效性[3]。因此，基于数理统计学考虑假设检验预测精度的问题，应用LARS算法选择变量，为阐述方便，定义参数为β，最小乘法估计为

(1)

式中，β—参数；ι—调节参数；n—最小二乘损失函数。根据LARS算法，定义乘法的剖面为最小二乘损失函数，即

(2)

式中，p>0；λ—调节参数；βJ—LARS估计值；J是一个正则化的问题，利用LARS算法进行求解[5]。

定义：当n→∞，λnn-1/2→0，β0=(β10，…，βp0)要满足渐近正态性和稀疏性[6]。

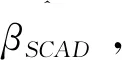
(3)

式中，调节参数λ的选择取决于系数，否则会发生同时选取p个λ的问题，造成计算搜索上的困难。需要注意的是，公式(2)中目标函数Q(β)在原点是奇异的，这给求解最小化造成一定的困难，为了解决这个问题，利用局部二次近似方法进行求解，具体求解过程如下：

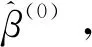
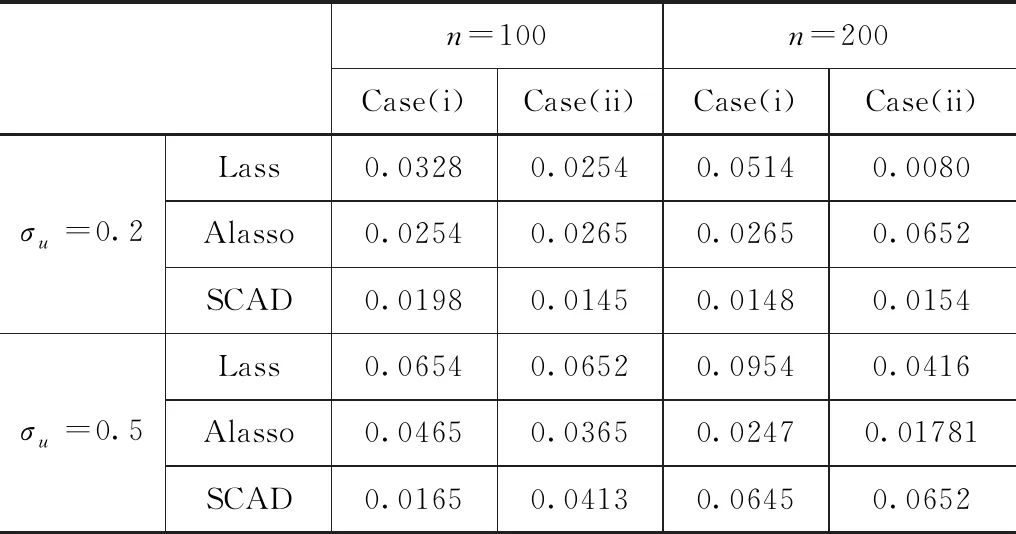
表1 缺失情形的变量选择

通过数值模拟可以调整计算的复杂度，从数值模拟结果可以看出，SCAD方法可以很好地改善估计的拟合精度，与预期的效果一样[7]。

1.2 假设检验显著性水平确定

在选择完水利水电工程质量监督数值统计学的假设检验变量后，要确定假设检验显著性水平，以此确定是否可以接受无效假设的概率标准，记假设水平为α，在假设检验应用中，通常取α为0.05或者0.01[8]。

根据小概率事件实际不可能性原理确定是否能够接受无效假设，通常在假设检验的过程中会出现两类错误，详见表2。

表2 数值统计学假设检验的两类错误

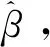
另外，需要注意的是，在假设检验时选用的显著水平不要超过0.05，要根据实验要求和实验结论选取显著水平。例如，在实验中，有许多不可控因素，会导致实验误差大，此时，可选择较低的显著水平。反之亦然，实验耗费较大，对精度的要求较高，不能反复进行，实验结论的应用事关重大，此时，要选择较高的显著水平，否则会直接影响假设检验的结论[4]。

1.3 数理统计学假设检验

在确定假设检验显著水平后，要考察基于数理统计学的假设检验应用问题，用检验模型考虑惩罚函数的影响，检验模型为

(4)

式中，ηi—测量误差，均值为0；Yi和wi—假定序列；εi—核函数[10]。

应用检验模型进行参数检验，具体步骤如下：

步骤一：假设wi和Yi来自检验模型的一组样本，则

(5)

式中，β—给定的参数；εi—核函数；δi—示性函数。如果Yi可以观测，则δ=1；若Yi不可以观测，则δ=0。

在公式(5)中，i是未知函数，依赖于Y和w，需要说明的是，如果w可以精准观测，则Y服从随机缺失机制;若w存在测量误差，计算所得的观测量则为变量w[11]。

步骤二：在满足Y和w的缺失机制后，要先获知参数β的有关先验信息，这些信息有利于提高参数估计的有效性，假设β满足如下约束条件：

Aβ=d

(6)

式中，A—已知的k×p矩阵，满足rank(A)=k；d—k的已知向量。

在满足上述约束条件下，为了模型的可识别性，要保证Y和w独立，需对其进行进一步讨论[12]。

步骤三：对有限样本的数值表现进行实际数据分析，用数值例子评价水利输电工程质量，假设数据来自以下模型：

(7)

式中，取Zi1～N(1，1)，ηi1～N(-2，1)，Zi2～N(0，σi2)。

应用公式(7)考察样本标准差，若MEE值变化小，说明估计对模型误差具有一定的稳健性；若MEE值变化大，说明得到的估计是相合的[13]。

由此，完成基于水利水电工程质量监督数理统计学的假设检验应用研究方法的设计。

2 仿真实验

为考察基于水利水电工程质量监督数理统计学的假设检验应用研究方法设计的合理性和逻辑性，采用数值模拟的方法对本次设计的方法和传统应用研究方法进行对比实验，考虑到缺失机制，需对两种研究方法进行1000次实验，选择三种不同的样本量，即n=50，100，150，假设约束条件为Aβ=d，d=3.5，A=(2，1)，显著水平为0.25，实验对比结果详见表3。

表3 缺失情形下的约束估计显著水平(α=0.25)

通过分析表3的数值结果，得到两种方法的测量误差对比结果，如图1所示。

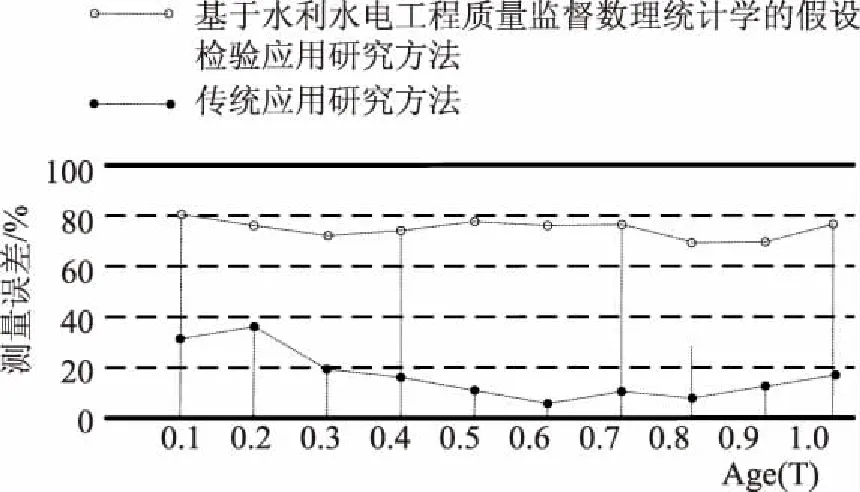
图1 两种方法测量误差对比结果

由图1可知，利用本文研究方法得到的测量误差值较小，无论在哪一种缺失机制下，MEE值变化较大，MEE值会随着样本量的增加趋于0，这意味着估计是相合的；而采用传统的研究方法测量误差时，MEE值变化较大，这意味着估计存在一定的差异。

综上所述，本文设计的基于水利水电工程质量监督数理统计学的假设检验应用研究方法具有一定的可行性，相比传统的研究方法更值得推广使用。

3 结束语

由于传统方法存在有偏参数估计，会影响测量精度，因此提出基于水利水电工程质量监督数理统计学的假设检验应用研究。引入LARS算法选择变量，来调整计算复杂度，并改善拟合精度；根据小概率事件实际不可能性原理确定是否能够接受无效假设，基于数理统计学的假设检验，通过检验模型考虑惩罚函数的影响。实验结果表明，不同缺失机制下本文方法的测量误差更小，证明所提方法更有利于水利水电工程的质量监督。由于实验环境与真实环境具有一定差异，实验结果会有一定偏差，但是不影响实验结论，接下来可以进一步研究所提方法的稳定性与安全性，来提高该方法的综合性能。