SiC模具高温模压石英玻璃物相接触角的分子动力学模拟

吴 悠，邹 斌，王俊成，黄传真，朱洪涛，姚 鹏

(1.山东大学机械工程学院先进射流工程技术研究中心，济南 250061；2.山东大学高效洁净机械制造教育部重点实验室， 济南 250061；3.山东大学机械工程国家级实验教学示范中心，济南 250061)

0 引 言

近年来，微结构光学元件因其在信息通信领域的广泛应用受到越来越多的关注。模压是制造光学玻璃元件常用的方法之一。模压过程中，一方面模具上精准的几何结构复印到了玻璃元件上；另一方面玻璃元件与模压模具之间的摩擦与粘附造成了模具的磨损，从而导致模具几何结构精度的丧失。这些均为模具与工件的固液界面相互接触、相对运动作用的结果。因此，有必要研究它们的接触特性，从而对模具结构和模压工艺的设计提供一定的指导。润湿是能够实现模压的先决条件，而接触角是表征润湿性的主要参数。对于理想光滑表面的接触角模型，Young[1]从固、液、气界面张力平衡的角度建立了经典的杨氏方程。对于粗糙表面和非均质表面，Wenzel[2]和Cassie[3]等学者在杨氏方程的基础上分别建立了Wenzel和Cassie-Baxter模型。Wenzel润湿模式中，液体始终完全浸渍粗糙结构波谷中，即出现所谓“钉扎”现象。而在模压工艺中，这一现象增大了工件液相在模具表面流动的阻力，从而增大了固液摩擦，使得模具更易磨损。而Cassie-Baxter润湿模式认为由于粗糙结构波谷中存在气相，液体无法浸渍其中，因此是模压比较期望的润湿模式。

在光学玻璃材料中，石英玻璃的光学性能有其独特之处。它既可以透过远紫外光谱，且透射率在同类材料中最优，又可透过可见光和近红外光谱。同时，其机械性能也高于普通玻璃[4]。目前，石英玻璃光学元件的制造多采用超精密磨削或是激光刻蚀的方法，生产效率低，生产成本高。而模压方法可以提高加工效率，实现大规模生产。然而，由于石英玻璃软化点温度高达1 500～1 600 ℃，常用的模具材料如WC等在此温度下无法正常工作，而SiC热稳定性好，熔点达2 830 ℃[5]，故较为适合作为模压石英玻璃的模具材料。由于模压温度高，超出了目前接触角测量仪器的工作范围，并且微结构模具表面粗糙度达到纳米级，要研究粗糙度对润湿性的影响需要测量纳米尺度微液滴的接触角，因此试验测定比较困难。分子动力学方法使微纳液滴高温接触角的模拟及研究其成因机理成为可能。

徐威等[6]通过改变LJ势函数中的作用参数模拟了纳米水滴在不同能量表面上的铺展过程和润湿形态，模拟结果与经典润湿理论计算得到的结果呈现相似变化趋势。王龙[7]研究了铜和金液滴在石墨烯和碳纳米管等不同结构基底上的润湿和融合过程，发现金属液滴的融合受液滴形状和基底结构影响。由于势函数的限制，目前对于界面润湿的分子动力学模拟多集中于LJ流体，如水和液氩等，而多元素流体较少见于报道。势函数按多体作用的复杂程度可分为对势和多体势。对于石英玻璃的模拟，多体势不能较好地计算Si-O键的断裂，因此不利于高温动力学性能的研究[8]。Beest等[9]基于石英玻璃经典的BMH势提出了BKS势，并运用第一性原理方法结合实验数据拟合了参数。Sundararaman等[10]使用BKS势预测了石英玻璃的力学性能，发现当短程和长程截止半径分别为5.5 Å和10 Å时模拟的石英玻璃结构更符合实际。Demiralp等[11]首先将Morse势与电荷平衡法(QEq)相结合，建立了MS-Q力场，并研究了石英玻璃在压力变化过程中的相变。丁元法等[12]比较了BKS与MS-Q模型下石英玻璃的高温扩散特性，认为计算高温下石英玻璃的扩散传输性能可优先选择MS-Q力场，但并未比较其表面特性。从以上文献可以看出，BKS和MS-Q是石英玻璃分子动力学模拟中常用的对势。其中，BKS势从低温到高温的较大温度范围均具有较好性能，而MS-Q势在高温下的传输性能要优于BKS势。目前对于石英玻璃高温表面特性的模拟的报道较为少见，因此仍需要对两种势函数性能的优劣进行比较。

Hosseini等[13]研究了不同形貌的疏水表面上的水滴行为，发现表面形貌、柱高度、空隙率和沉积角是影响表面疏水性的主要参数。因此，本模拟在SiC表面构建了纳米方柱阵列，并分别使用粗糙度评定参数Ra和Rmr表示柱高和空隙率，研究了纳米级表面粗糙结构对面向高温模压的SiO2/SiC接触角的影响。

本文使用分子动力学方法，对比了分别采用BKS和MS-Q势函数计算的SiO2熔体高温表面张力。模拟了不同模压温度和SiC模具表面粗糙结构SiO2的高温接触角，研究了微尺度下的高温界面润湿特征和SiO2熔体表面层结构特点，本研究的结构框图如图1所示。

1 模拟方法和模型

1.1 界面张力的计算

为了保证成形精度并减小工件与模具的粘附，光学玻璃模压温度一般选择在转变点温度到软化点温度之间[14]，故选择石英玻璃实际软化点附近温度1900 K作为模拟温度。SiO2表面张力模拟系统如图2所示。SiO2熔体表面模型的建立方法是在模拟盒子中随机加入800个Si原子和1 600个O原子，使其密度约为2.2 g/cm3。随后在5 000 K下驰豫200 ps以消除初始构型的影响，并以100 K/20 ps的速度降温至1 900 K。最后在x轴方向模型两边各添加一厚度为20 Å的真空层，以避免周期性边界的影响。面向高温模压的SiO2/SiC界面张力模拟系统如图3(c)所示，其中SiC是由金刚石结构的β-SiC原胞排列而成。分别将SiO2和SiC单独在1 900 K下驰豫200 ps，然后将它们添加进同一模拟盒子中，使SiO2与SiC {100}表面接触并对整个体系进行驰豫。

图1 基于分子动力学的SiC模具高温模压石英玻璃的物相接触角模拟研究关系框图
Fig.1 Study relationship of high temperature contact angle of molded optical glass in SiC die based on molecular dynamics

图2 SiO2熔体表面张力模拟计算体系
Fig.2 Simulation system of SiO2melt surface tension

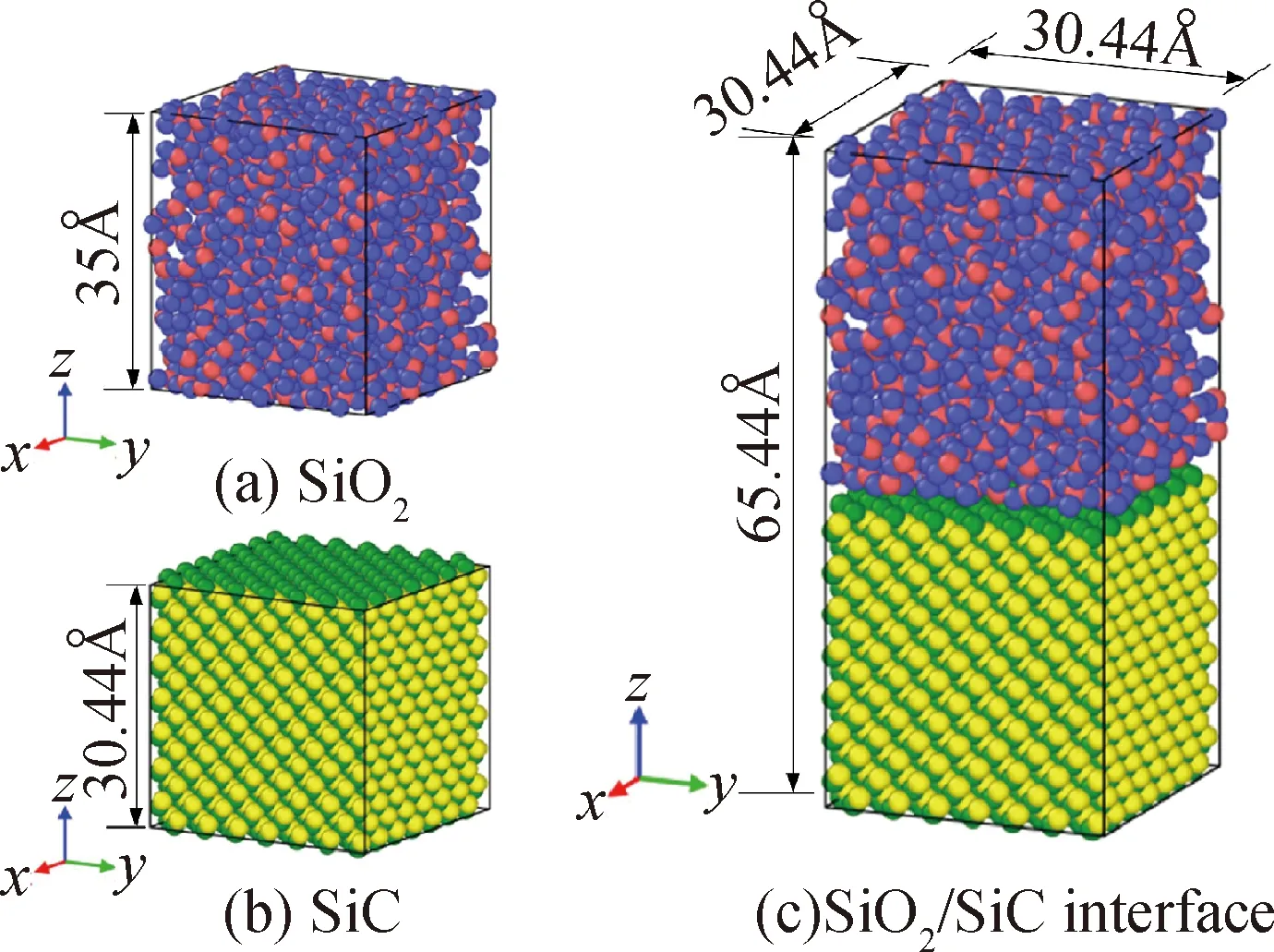
图3 SiO2/SiC高温界面张力模拟计算体系
Fig.3 Simulation system of SiO2/SiC high temperature interface tension

表面与界面张力的计算均采用压力张量法[15]，

(1)

式中，γ表示表面张力；Lx为模拟体系在x方向的长度;因子1/2是由于模拟系统有两个界面；PN与PT分别为系统界面法向和切向压力张量分量。

(2)

(3)

式中，kB为玻尔兹曼常数；V为模拟盒子体积；U表示势函数;ρ为液体密度；T为温度；r为原子间距，x、y、z为其在三个坐标轴方向的分量。

为了比较不同势函数模拟界面张力的可靠性，在模拟中，SiO2原子间的相互作用先后用BKS[10]和MS-Q[11]势函数进行表征如下，势函数参数见表1。

(4)

(5)

式中，q表示电荷量；A、C、D均为与相互作用强度有关的参数；α为与平衡距离有关的参数。

表1 SiO2势函数参数Table 1 Parameters of potentials for SiO2

SiC原子间的相互作用使用tersoff势函数表征。由于SiO2/SiC界面间为范德华作用，因此使用LJ势函数表征，其参数来自于UFF力场[16]，如表2所示。

表2 SiO2/SiC势函数参数Table 2 Parameters of potential for SiO2/SiC interaction

模拟过程中，模拟盒子三个方向均为周期性边界。BKS势函数Si和O原子所带电荷分别为+2.4e、-1.2e，截断半径为5.5 Å；MS-Q势函数Si和O原子所带电荷分别为+1.318e、-0.659e，截断半径为9 Å。静电力的计算采用PPPM(Particle-Particle Particle-Mesh)方法且精度为10-5，截断半径为10 Å。时间步长为1 fs。模拟均在正则系综(NVT)下进行，调温使用Nosé-Hoover方法。

1.2 接触角的模拟

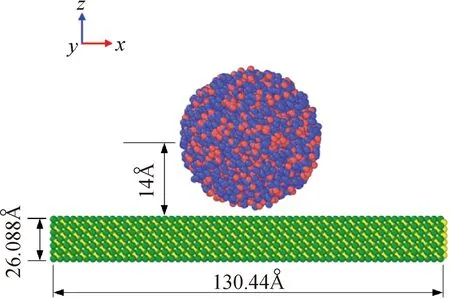
图4 面向高温模压的SiO2/SiC接触角模拟系统Fig.4 Simulation system of SiO2/SiC contact angle for high temperature molding

在模拟系统中SiO2与SiC分别为液相和固相，其中，SiC基底为SiC单胞排列而成的超晶胞，对其作出三点假设：(1)假设SiC表面为不存在缺陷的理想表面；(2)由于SiC不同晶面表面能相差较小，假设其{100}晶面为与SiO2相接触的表面；(3)假设SiO2熔体液滴为理想的球形。接触角的模拟系统如图4所示，首先在半径2.348 Å的球体区域随机添加1 200个Si原子和2 400个O原子，随后在5 000 K下驰豫200 ps并以100 K/20 ps的速度降温至1 900 K得到模拟所用的SiO2液滴模型。最后将SiO2和SiC添加进同一模拟盒子，x、y方向使用周期性边界，z方向使用固定和镜像边界，其他设置与上一节相同。

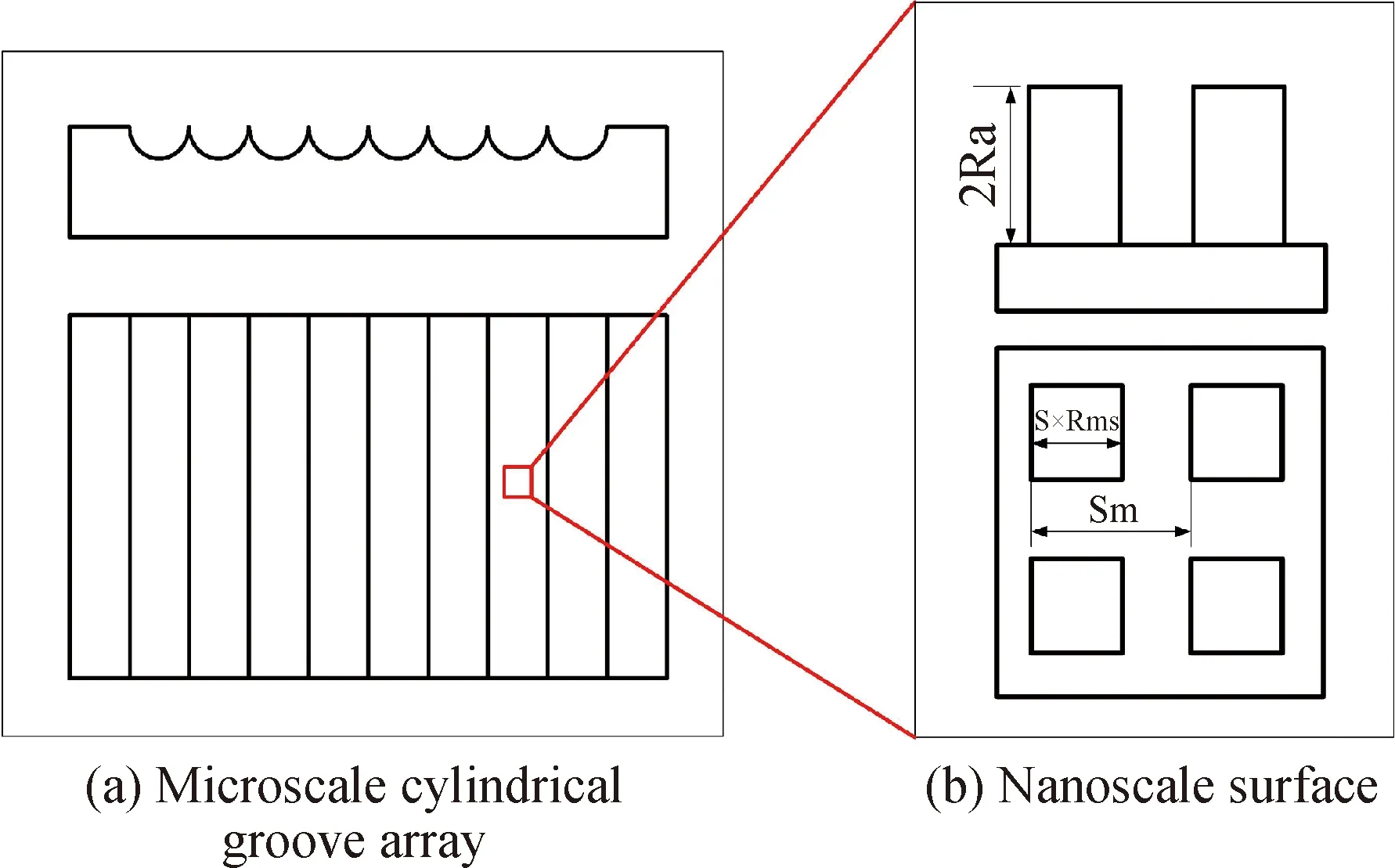
图5 微结构阵列模具表面多尺度形貌示意图Fig.5 Multiscale surface topography of micro-structure array die

为了研究纳米级表面粗糙结构对接触角的影响，采用文献[13]的方法构建了方柱形阵列SiC壁面。其结构如图5所示。Wenzel[2]和Cassie-Baxter[3]模型可用式(6)、(7)表示：

cosθW=rcosθY

(6)

cosθC=fcosθY+f-1

(7)

式中,θY为本征接触角；θW与θC为Wenzel和Cassie-Baxter模型接触角;r为粗糙度因子，表示表面的实际面积与表观面积之比；f为接触面积分数，表示液滴与基底实际接触的面积和基底表观面积之比。r与f可用粗糙度评定参数表示为

(8)

f=Rmr2

(9)

式中,Ra为轮廓算数平均偏差，Rmr为轮廓支承长度率，Sm为轮廓微观不平度的平均间距。模拟中若Rmr、Sm取恒值，则Ra取0.25、0.5、1、1.5倍晶格参数，分别对应r值为1.5、2.0、3.0、4.0；若Ra取恒值，改变柱间距为2、1.5、1、0.5倍晶格参数使Rmr取0.33、0.40、0.50、0.67，分别对应f值为0.11、0.16、0.25、0.44。

2 模拟结果与讨论

2.1 界面张力

图6为1 900 K下BKS与MS-Q模型中SiO2熔体表面张力随时间的演化。由于使用压力张量法时系统需要较长时间稳定，模拟连续进行了20 ns。为了降低模拟初期结构不稳定的影响，在计算累计平均值时采用最后10 ns数据。BKS与MS-Q势函数的计算结果分别为0.410 N/m和0.390 N/m。由文献[17]可知，SiO2在1 900 K下的实际表面张力应为0.302 N/m左右。考虑到模拟本身的准确性以及实际实验过程中，氧分子等充当表面活性剂降低了测定的表面张力值，因此模拟值高出实验值0.07～0.11 N/m左右是可接受的[18]。可以看出MS-Q势函数的模拟结果比BKS势函数更为接近实验值。

图6 BKS势函数与MS-Q势函数下SiO2熔体表面张力演化
Fig.6 Evolution of SiO2melt surface tension using BKS potential and MS-Q potential

图7为两种不同势函数模拟的面向模压的SiO2/SiC高温界面张力演化图。界面张力系统达到稳定时间相对较短，因此模拟时间设为15 ns，取最后4.5 ns时间段的数据计算平均值。从图中可见，BKS和MS-Q势函数的模拟结果分别为0.846 N/m和0.682 N/m。同时，计算了两种表面模型的一维密度分布和径向分布函数(Radial Distribution Function,RDF)。图8(a)为模型中心至模拟盒子边缘的密度分布，BKS与MS-Q模型的表面均存在类似汽液共存界面的低密度相，其厚度分别为4 Å与6 Å。BKS模型内部的密度约为2.69 g/cm3，大于MS-Q的2.25 g/cm3。这说明BKS表面模型的密度大于MS-Q模型，因此原子间距要小于MS-Q模型，具有更强的原子间作用力，从而具有更大的表面张力。图8(b)中RDF的计算结果也支持了这一解释。RDF图中前三个峰代表O-O、Si-O、Si-Si原子对的第一近邻，峰值点的横坐标即原子对的键长，其数值如图8(b)所示，MS-Q模型中数量较多且强度较大的Si-O、O-O键长均大于BKS模型，从而导致其表面张力小于BKS模型。综上所述，高温模压时SiO2表面性质的模拟可优先选择MS-Q势函数。

图7 面向高温模压的SiO2/SiC界面张力演化过程
Fig.7 Evolution of SiO2/SiC interface tension for high temperature molding

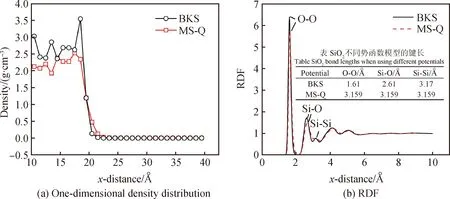
图8 使用BKS与MS-Q势函数的SiO2表面结构对比
Fig.8 Comparison of SiO2surface structure using BKS and MS-Q potential

2.2 表面粗糙结构对接触角的影响

液滴在理想光滑表面上的接触角称为本征接触角。由于微纳尺度下液滴表面存在一定的密度和压力涨落，为了获得具有统计学意义的接触角值，在处理数据时采用等密度拟合曲线法[19]。最后得到面向高温模压的SiO2/SiC的本征接触角为119.25°。根据杨氏方程[1]，可以利用上节模拟得到的界面张力对本征接触角进行检验。

(10)

式中,γsv表示固-气界面能；γsl与γlv分别表示固-液界面能和气-液界面能，它们在数值上与固-液界面张力和液体表面张力相等。由上节可知，γsl和γlv的值分别为0.682 N/m和0.390 N/m。由于本模拟中采用的SiO2/SiC相互作用参数来自UFF力场，因此选择文献[20]中使用UFF力场算得的SiC{100}晶面表面能数值0.502 N/m代入式(10)。最终得到的本征接触角理论值为117.49°，与模拟数值差别不大。

图9是SiO2熔体在具有不同粗糙度因子的SiC模具表面上接触角的模拟，从图中可见，接触角总体值在135°左右波动。接触角变化不大则表明固液相互作用能较为稳定，但图9(b)显示，在r=1.5时固液相互作用能较大。由图10可以看出，当粗糙度因子r=1.5时，SiO2熔体浸润了沟槽，出现“钉扎”现象，此时润湿接近于Wenzel状态。“钉扎”现象增强了固液界面的摩擦，液滴的铺展需要克服更大的能垒，因此虽然固液相互作用能较大但并未使液滴接触角减小；r>1.5时，SiO2均处于Cassie-Baxter润湿状态，因此接触角不再受粗糙度因子变化的影响。从Cassie-Baxter状态到Wenzel状态的过渡称为润湿转变。润湿转变可以通过施加压力实现，但临界转变压力会随着纳米柱的高度减小而减小[21]；当其减小到一定程度，就可能仅仅依靠系统压力实现润湿转变。本研究中，当r>1.5时系统压力无法使液滴保持Wenzel状态，因此转变为Cassie-Baxter状态；而此状态下，界面的固液相互作用比Wenzel状态更低，液滴在固体表面的扩散系数变小[22]，说明此时SiO2熔体在剪切作用下更易在SiC模具表面滑移，从而导致粘性摩擦作用较小。

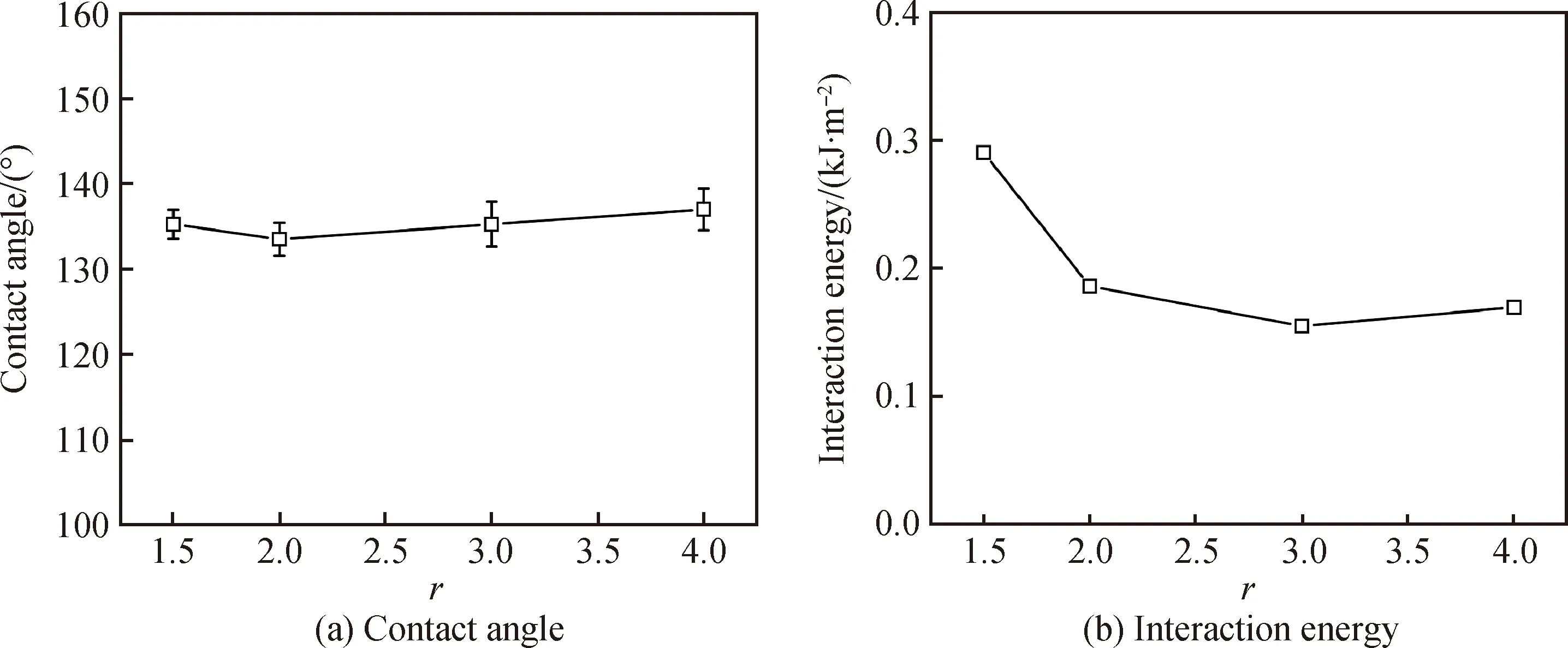
图9 SiC模具表面粗糙度对SiO2熔体液滴接触角和两者相互作用能的影响
Fig.9 Effect of SiC die roughness on contact angle of SiO2melt droplet and interaction energy

图10 SiC模具表面粗糙度对SiO2熔体液滴 接触状态的影响
Fig.10 Effect of SiC die roughness on contact state of SiO2melt droplet

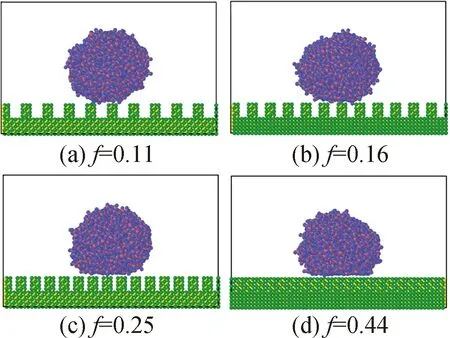
图11 接触面积分数对面向高温模压的SiO2/SiC 接触状态的影响
Fig.11 Effect of contact area fraction on SiO2/SiC contact state for high temperature molding

图12 接触面积分数对面向高温模压的SiO2/SiC接触角和相互作用能的影响
Fig.12 Effect of contact area fraction on SiO2/SiC contact angle and interaction energy for high temperature molding

图11为粗糙度因子r>1.5时SiC模具表面接触面积分数对SiO2熔体液滴接触状态的影响，此时SiO2始终呈现Cassie-Baxter润湿状态，液滴随接触面积分数的增大逐渐在SiC表面铺展。图12(a)对比了模拟接触角和理论接触角，虽然两者存在一定误差，但其都随着接触面积分数的增大而减小；同时图12(b)显示接触角越小，SiO2/SiC高温模压界面具有越强的相互作用。表面粘着力和热应力是脱模力的两个组成部分[23]，减小轮廓支承长度率即减小了SiO2与SiC模具界面的实际接触面积，从而能减小工件和模具之间的表面粘着力。而Cassie-Baxter润湿模式无“钉扎”现象，减小了工件和模具的传热面积，在一定程度上减小了热应力。因此适当减小Rmr值可以降低以及工件与模具之间的脱模力，从而减小模具磨损，提高寿命。同时也缩减了模具制造过程中抛光工序的工作量。

2.3 温度对接触角的影响

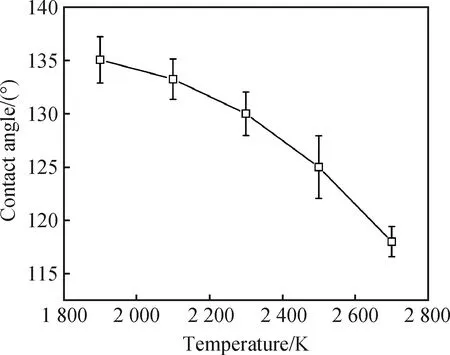
图13 面向高温模压的SiO2/SiC接触角与温度的关系Fig.13 Relationship between SiO2/SiC contact angle and temperature for high temperature molding

图13为接触面积分数为0.25时温度对面向高温模压的SiO2/SiC接触角的影响。从图可见，接触角值随温度的增大而减小，说明温度升高SiO2的表面张力减小；当温度高于2 300 K时，接触角的变化较大，这是因为使用MS-Q势函数模型的SiO2自扩散激活温度约为2 300 K左右[12]。自扩散激活温度可以视作石英玻璃的软化点温度，在此温度附近，石英玻璃的结构发生较大变化，松动和新生的化学键均大大增加[24]。图14(a)是不同温度下SiO2熔体表面的结构特点，由图可见，SiO2熔体表面存在一个等密度层；在等密度层外部，密度随温度升高而增大；在等密度层内部，密度随温度升高而减小；这意味着SiO2熔体内部的原子在高温作用下逐渐向外扩散，这种密度梯度的减小使SiO2表面结构更加松散，减小了其表面张力。图14(b)还表明，温度对SiO2熔体表面原子化学键的键长并未产生较大影响，但随着温度升高，各化学键对应的峰值依次减小，表明表面层原子的无序程度增加。同时，对比图8(b)可以发现，表面层中Si-Si对应的峰值变得较为微弱甚至消失，这说明在表面层硅原子数量较少，而氧原子大量聚集，O-O键的强度远小于Si-O键强度，这可能是SiO2表面张力随温度减小的另一个原因。

图14 不同温度下SiO2熔体表面结构特点
Fig.14 Surface structure of SiO2melt in different temperature

3 结 论

采用分子动力学方法模拟了SiO2熔体的界面结构，将SiC模具纳米级表面理想化为纳米方柱阵列，研究了粗糙度和温度对面向模压的SiO2/SiC高温接触角的影响，得到以下结论：

(1)使用MS-Q势函数模拟的SiO2熔体表面张力比BKS势函数计算的结果与实验值更为接近，因此模拟SiO2高温熔体的表面性质使用MS-Q势函数更为合理。

(2)在1 900 K的模压温度下，当粗糙度因子r>1.5时，Ra的变化对接触角值无明显影响。Rmr值减小使得接触面积分数f减小，接触角值随之增大。此时润湿模式从Wenzel转变为Cassie-Baxter，减小了工件-模具之间的摩擦。由于热应力和界面粘着力的减小，石英玻璃光学元件模压后的脱模力将会降低。同时，由于降低了Rmr值的要求，SiC模具加工过程中抛光工序的工作量也相应得到了减小。

(3)面向高温模压的SiO2/SiC的接触角随模压温度升高而减小。当模压温度超过2 300 K时，接触角变化率显著增大。因此模压温度选择在2 300 K以下可以降低模压时模具因玻璃熔体的粘附造成的磨损。