考虑结构整体特性的钢筋混凝土框架震后残余侧移响应研究
韩建平 高 珺 孙小云 拜立岗
(1.兰州理工大学甘肃省土木工程防灾减灾重点实验室,兰州730050;2.兰州理工大学防震减灾研究所,兰州730050;3.同济大学土木工程学院,上海210092)
0 引 言
基于不同地震激励水平下的结构分析结果进行抗震性能评估是基于性能地震工程的主要研究内 容 之 一[1]。 目 前 采 用 的 工 程 需 求 参 数(Engineering Demand Parameters,EDPs)以基于地震作用下的瞬时响应或累积能量耗散为主,特别是结构整体水平和构件水平的最大位移响应和其自身的延性能力。对历次灾害进行理论和调查研究结果均表明,结构体系经历地震作用之后,残余变形对结构体系损伤评价和性能评估有不可忽视的作用,可以考虑将其视为常见结构体系损伤和性能评价的补充指标[2-3]。
1995 年日本在经历阪神地震后,调查研究表明有超过100 根钢筋混凝土柱由于残余层间侧移角大于1.5%,虽然在地震中未发生倒塌但无法继续使用导致不得不拆除[4]。此后,各国开始将结构残余变形作为抗震中的问题之一进行研究,《日本公路桥梁设计规程第V部分:抗震设计》提出了桥墩震后残余位移限值的规定[5]。McCormick 等对日本东京大学一幢既有建筑进行研究,结果表明:当建筑的残余侧移角达到0.5%时,住户就会有感知;大于0.5%,则住户就有眩晕和恶心的感觉[6]。Kawashima 等提出了残余位移反应谱的概念[4]。Christopoulos[2-3]分别对单自由度(SDOF)和多自由度(MDOF)体系进行研究,发现分析时采用不同的滞回特性、非弹性机理以及地震动强度指标等,对结构残余位移响应影响较大,同时提出高阶振型和P-Δ效应对结构残余位移的影响不容忽视,通过联合使用最大位移角和残余位移角建立性能指标矩阵,从而定义结构体系的总体性能水平。Ruiz-Garcia 等的研究表明,钢框架残余位移的大小与分布对地震动烈度、结构层数、自振周期、框架机制以及模型所采用不同的滞回特性等都很敏感,并且强调了对残余位移估计时的不确定性[7]。Yazgan 对残余位移响应的可靠预测以及所需的恰当数值模型做了深入的研究,通过对比试验结果,提出了基于概率的、考虑残余变形的震后损伤评估方法[8]。Hatzigeorgiou 等基于SDOF体系的不同影响参数,推导出一个简洁、可靠的经验方程,旨在根据地震作用下的体系残余变形估算出体系最大变形[9]。
目前,残余位移这一指标的研究在我国主要集中于SDOF 体系。欧阳承新等研究了对不同结构参数,如阻尼比、自振周期、采用不同滞回特性等的SDOF 体系,输入地震动记录后研究体系残余位移[10]。叶列平等研究发现,屈服后刚度系数γ越大,结构残余位移越小[11]。郝建兵等研究了双线性SDOF 体系在不同强度折减系数和屈服后刚度系数情况下,体系残余位移与地震动强度指标之间的相关性,建议在计算体系残余位移时,以PGV强度指标作为地震动记录的主要指标[12]。余波等通过对桥梁结构进行大量非弹性动力分析,并对SDOF 体系定量分析了P-Δ效应、规一化屈服强度等结构残余位移的概率统计特征影响,结果表明残余位移与峰值位移之间的相关性[13]。
本文通过对3 个楼层数不同的多高层钢筋混凝土框架结构进行静力推覆分析,将3 个结构的pushover 曲线简化成三线性,从而得到结构整体性特性指标如屈服后刚度比和下降段刚度比,进而对3 个结构分别进行3 个强度水平、22 条地震动记录下的弹塑性时程分析,计算得到最大层间位移角和最大残余层间位移角的平均值、标准差和变异系数,并对结构整体特性如结构基本自振周期、屈服后刚度比、下降段刚度比等对最大层间位移角和最大残余层间位移角的影响和最大层间位移角与最大残余层间位移角之间的相关性进行了分析讨论。
1 结构模型和地震动选择与调整
1.1 结构概况与分析建模
首先依据我国现行《建筑抗震设计规范》(GB 50011—2010)[14]进行抗震设计,采用 PKPM系列软件对图1所示5层、8层和11层钢筋混凝土框架结构公寓楼进行建模分析计算。3 个结构所在地抗震设防烈度为8 度,设计基本地震加速度为0.20g,设计地震分组为第三组,Ⅱ类场地。混凝土强度等级均采用C35,受力主筋采用HRB400钢筋,箍筋采用HPB300 钢筋。不上人屋面,屋面活荷载标准值为0.5 kN/m2,楼面活荷载标准值为走廊2.5 kN/m2、其他部分2.0 kN/m2。第1 层层高为3.9 m,其余各层层高均为3.6 m,5 层、8层和11 层结构的总高度分别为18.3 m、29.1 m 和39.9 m。

图1 钢筋混凝土框架平面布置图(单位:mm)Fig.1 Floor plane of RC frame structure(Unit:mm)
根据图1 所示的结构平面布置图,取图中阴影部分即一榀横向框架作为计算单元。以5 层框架结构为例,其结构计算简图及配筋如图2 所示,利用OpenSees 有限元软件进行建模分析。采用中心线模型,以基于材料本构关系的纤维单元作为非线性分析模型,混凝土本构关系模型采用考虑抗拉的Concrete02,钢筋本构关系模型采用可考虑强度退化的ReinforcingSteel,梁柱单元均采用基于位移的梁柱单元(Displacement-Based Beam-Column Element),每个柱单元设置 5 个积分点。几何坐标转换选用P-Delta 转换(P-Delta Transformation),即考虑结构的P-Δ效应,楼板平面采用完全刚性假定。
1.2 地震动记录选择与调整
1.2.1 地震动记录选择
影响结构响应的地震动特性主要有幅值、频谱特性和持时。以2010 规范设计反应谱为目标谱,基于谱匹配方法从太平洋地震工程研究中心(PEER)地震记录数据库中选取22 条地震动记录,选择重要持时Ds(Significant Duration)作为强震持时[15-16]。为了避免重要持时变动过大,所选地震动记录的重要持时处于10~40 s。选取的地震动记录如表1所示。

表1 选取的地震动记录Table 1 Selected ground motion records
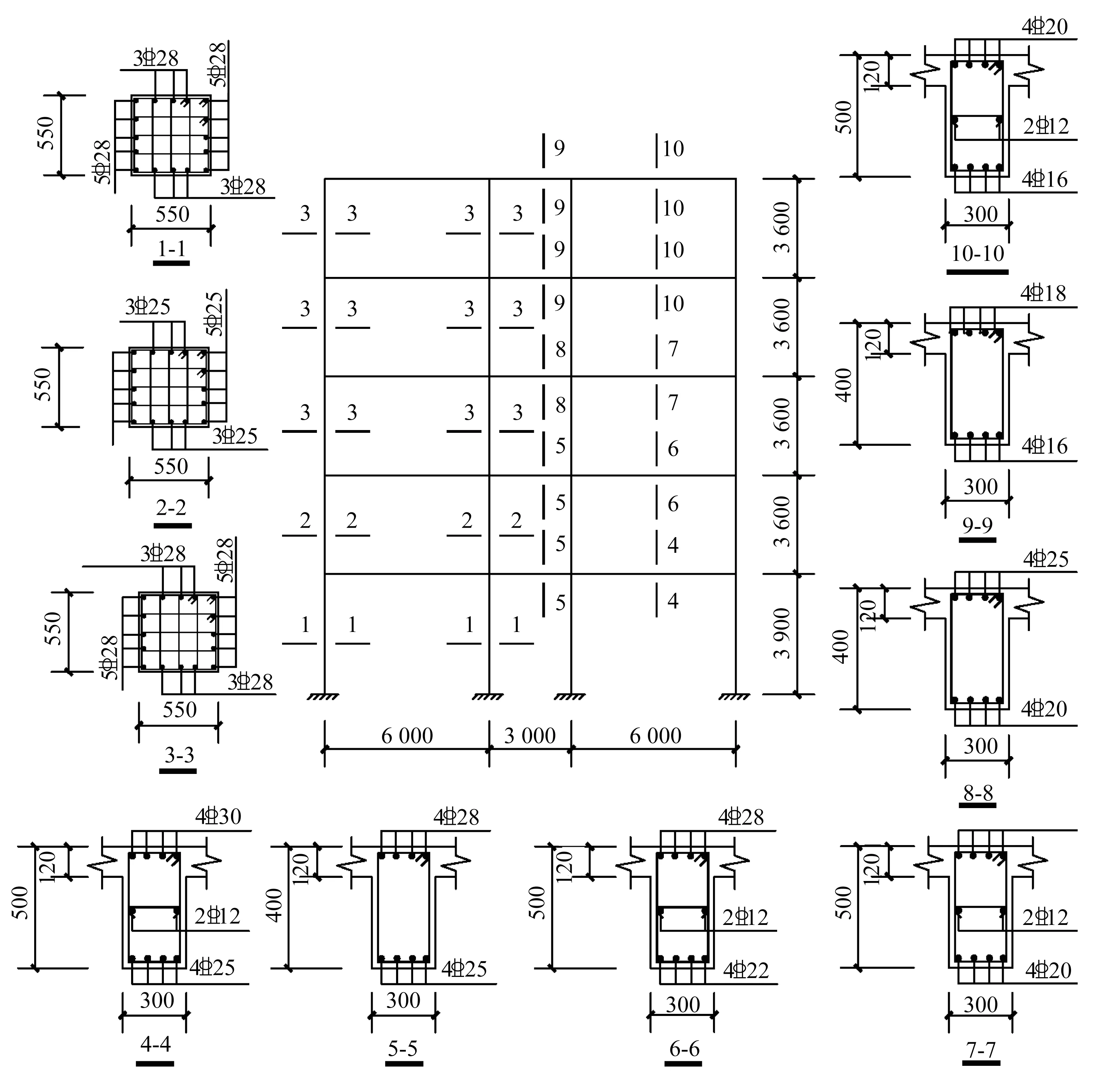
图2 5层钢筋混凝土平面框架结构模型Fig.2 Structural model of 5-story RC planar frame structure
1.2.2 地震动记录调整
与规范谱匹配前后的地震动记录的加速度反应谱分别如图3(a)和图3(b)所示。以匹配后的平均加速度反应谱平台段的谱值A 作为地震动强度指标,为了研究不同地震动记录强度水平下3 个结构模型的地震响应的大小和分布,将选取的地震动记录分别调整到水平1(A=0.9g)、水平 2(A=1.2g)和水平 3(A=1.4g),分别对应 8 度(0.2g)、8度(0.3g)和9度的罕遇地震水准。

图3 地震动记录加速度反应谱Fig.3 Acceleration response spectra of ground motion records
2 结构静力推覆分析
首先分别对3个结构模型进行模态分析,得到基本自振周期T1和第一振型向量Φ1。5层、8层和11 层结构基本自振周期分别为0.72 s、1.02 s 和1.42 s。取目标位移为1 000 mm,按F1=MΦ1分别对5层、8层和11层结构模型施加侧向水平力进行推覆分析,得到基底剪力和顶点位移的关系曲线,即结构的第一振型推覆曲线[17-18],如图4所示。

图4 结构第一振型推覆曲线Fig.4 First-mode pushover curves of structures
图4 结果表明,当顶点达到设定的目标位移1 000 mm 时,3 个结构的推覆曲线均出现了下降段,且每条曲线具有相似的规律,即加载初期近似于一条通过原点的直线;随着顶点位移的增大,结构刚度开始减小,结构出现强化段直至基底剪力达到峰值;过峰值点后,曲线出现下降段。据此将第一振型推覆曲线等效为三直线型曲线,如图5所示。
现以5层结构为例,通过图6说明等效及相关参数产生的过程:
(1)弹性段:以y=K5-1x+B5-1表示,直线过原点,截距B5-1为0,只需确定斜率参数K5-1,即确定结构的初始刚度。
(2)屈服段:以y=K5-2x+B5-2表示,直线通过原始曲线的峰值点,依据能量等效原理,原始曲线与坐标轴围成的面积与等效曲线与坐标轴围成的面积相等。

图5 结构等效三线形推覆曲线Fig.5 Equivalent trilinear pushover curves of structures

图6 5层结构第一振型推覆曲线及等效三线形推覆曲线Fig.6 First-mode pushover curve and its equivalent trilinear pushover curve of 5-story structure
(3)下降段:以y=K5-3x+B5-3表示,连接峰值点和位移最大处点的直线即为下降段,其中K5-3为下降段斜率,表示结构的负刚度。
基于此方法,分别求出3个结构模型的等效三线形推覆曲线各直线段方程的参数,如表2 所示。同时表2 中也给出了三个结构模型的屈服后刚度比和下降段刚度比。同样以5层结构为例,屈服后刚度比定义为屈服段刚度与初始刚度的比值,以α5=K5-2/K5-1表示,下降段刚度比定义为下降段刚度与初始刚度的比值,以β5=K5-3/K5-1表示。

表2 等效三线形推覆曲线各直线段方程参数Table 2 Parameters of straight line segments of equivalent trilinear pushover curves
表2 结果表明,随着结构层数的增加,即随着结构高宽比的增大,结构的初始刚度变小,屈服段的刚度也略有减小,下降段的刚度则无明显变化,而屈服后刚度比和下降段刚度比的绝对值则变大。
3 弹塑性时程分析
3.1 弹塑性时程分析结果统计
将调整到水平1、水平2和水平3的22条地震动记录分别输入3 个不同层数的结构模型,进行弹塑性时程分析。本文为研究结构静止后的残余位移,在每条地震动记录原持时的基础上增加10 s零强度持时,使结构做自由振动直至静止。分析得到每个结构在每条地震动记录作用下的最大层间位移角(IDRmax,Maximum Inter-story Drift Ratios)和最大残余层间位移角(RIDRmax,Maximum Residual Inter-story Drift Ratios),分别计算得到每个结构在相应地震动强度水平下两个指标的均值、标准差和变异系数,如表3所示。

表3 最大层间位移角、最大残余层间位移角的均值、标准差以及变异系数Table 3 Mean,standard deviation and variation coefficient values of maximum inter-story drift ratio and maximum residual inter-story drift ratio of the structures
表3 结果表明,对同一结构,最大层间位移角和最大残余层间位移角的均值均随地震动强度水平的提高而增大;最大层间位移角响应的离散性随着地震动水平的提高而增大,而最大残余层间位移角的离散性则无此规律。同一地震动强度水平下,最大层间位移角和最大残余层间位移角的均值随着楼层数的增加而增大;最大层间位移角的离散性随着楼层数的增加而增大,且最大残余层间位移角的离散性也基本上遵循此规律,但没有最大层间位移角响应的规律性明显。
3.2 最大层间位移角和最大残余层间位移角沿结构高度的分布
5 层、8 层、11 层结构在 3 个不同地震动强度水平下的最大层间位移角和最大残余层间位移角的均值沿结构高度的分布分别如图7 和图8所示。

图7 最大层间位移角沿楼层高度的分布Fig.7 Distribution of the maximum inter-story drift ratios along structural height

图8 最大残余层间位移角沿楼层高度的分布Fig.8 Distribution of the maximum residual inter-story drift ratios along structural height
图7、图8结果表明,随着楼层数的增加,结构的最大层间位移角和残余层间位移角也呈增大趋势。
3.3 屈服后刚度比对最大残余位移角响应RIDRmax的影响
依据静力推覆分析结果,得到不同结构对应的整体特性屈服后刚度比α和下降段刚度比β。在不同的地震动强度水平下,不同屈服后刚度比所对应结构在22 条地震动记录输入下的最大残余层间位移角平均值如图9所示。
图9 结果表明,3 个不同的地震动强度水平下,最大残余层间位移角的均值均随着屈服后刚度比的增大而增大,且其离散性也随着结构屈服后刚度比的增大而增大。对于单自由度体系,结构的屈服后刚度比是影响结构残余位移响应最关键的因素,即残余位移响应随着屈服后刚度比的增大而减小[19]。而多自由度体系钢筋混凝土结构的屈服后刚度比,作为结构的整体特性受结构的高度、质量、构件尺寸等多重因素的影响,这与单自由度的屈服后刚度比对结构残余位移响应的影响规律不同甚至截然相反。
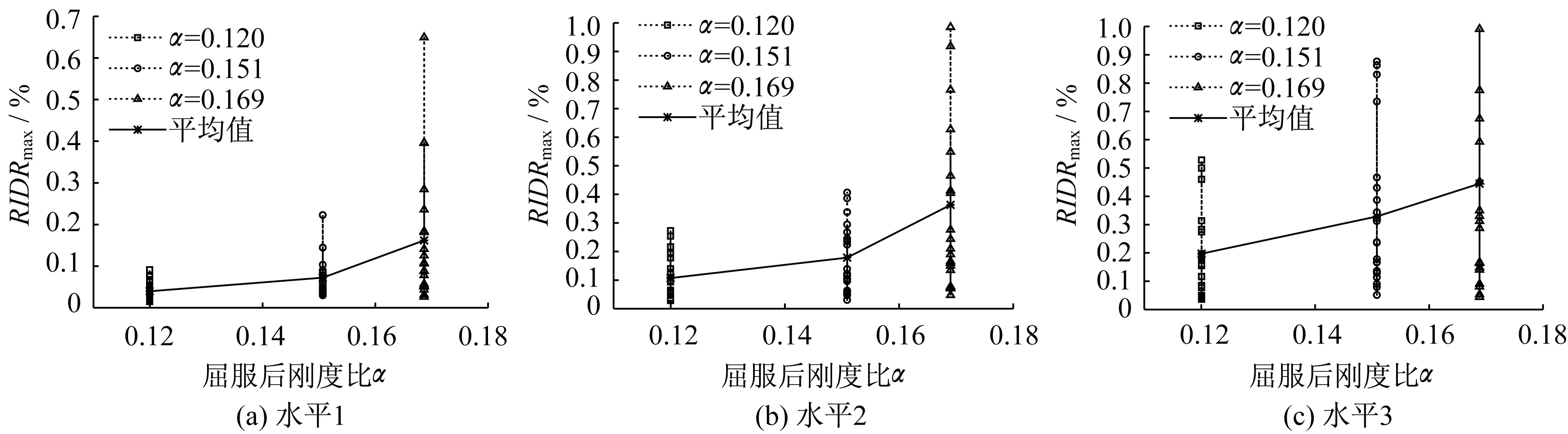
图9 屈服后刚度比对最大残余层间位移角的影响Fig.9 Effect of post-yielding stiffness ratios on maximum residual inter-story drift ratios
3.4 下降段刚度比对最大残余位移角响应RIDRmax的影响
在不同的地震动强度水平下,不同下降段刚度比所对应结构在22 条地震动记录输入下的最大残余层间位移角平均值如图10所示。
图10 结果表明,3 个不同的地震动强度水平下,最大残余层间位移角的平均值均随着下降段刚度比的绝对值的增大而增大;同时,其离散性也随着结构下降段刚度比的绝对值的增大而增大。与屈服后刚度比的影响类似,多层钢筋混凝土结构下降段刚度比对最大残余层间位移角的影响与单自由度体系下降度刚度比对残余层间位移响应的影响规律不同。
3.5 结构基本自振周期对最大层间位移角和最大残余层间位移角响应的影响
结构周期,特别是结构的基本自振周期,是结构本身最重要的整体性特性,因为它包含了结构的整体质量和抗侧刚度的信息[20]。结构基本自振周期对最大层间位移角和最大残余层间位移角在不同地震动强度水平下的影响如图11所示。
图11 结果表明,最大层间位移角和最大残余层间位移角均随着结构周期和地震动强度水平的增大而增大。结构响应,特别是最大残余层间位移角响应,受结构基本周期的影响相当明显。
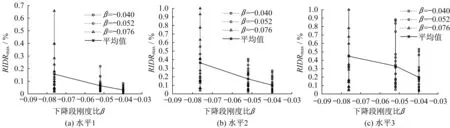
图10 下降段刚度比对最大残余层间位移角响应的影响Fig.10 Effect of post-capping stiffness ratios on the maximum residual inter-story drift ratios

图11 结构基本自振周期对最大位移响应和最大残余位移响应的影响Fig.11 Effect of fundamental vibration periods of structures on the maximum inter-story drift ratios and maximum residual inter-story drift ratios
3.6 最大层间位移角响应和最大残余层间位移角响应的相关性
为了通过层间位移角响应来估算残余层间位移角响应,利用线性相关系数ρ研究二者之间的相关性。图12 给出了三种不同结构模型在不同地震动强度水平下最大层间位移角IDRmax和最大残余层间位移角RIDRmax之间的线性相关系数沿着楼层的分布。
图12 结果表明,结构底部楼层的IDRmax和RIDRmax的相关性较好,随着楼层上移,两者的相关性趋弱。对于最大位移响应和残余位移响应均比较大的底部楼层,在较大的地震动强度水平下,其相关性一般都较大。这说明结构进入非线性越强,最大位移响应和残余位移响应的相关性越大。对于不同高度的结构而言,随着地震动强度水平的增大,两者的相关性沿着结构高度的分布没有明显的规律。
4 结 论
通过对3 个多高层钢筋混凝土框架结构进行静力推覆分析和22条地震动记录在3个不同地震动强度水平下的弹塑性时程分析,研究整体结构特性对钢筋混凝土框架包括残余位移指标的响应影响,得到结论如下:
(1)在同一地震动强度水平作用下,多高层钢筋混凝土框架结构的楼层数越多,最大层间位移角和最大残余层间位移角响应也越大。最大层间位移角响应的离散性随着楼层数的增加而增加,且残余层间位移角的离散性也基本上符合这一变化规律,但其变化没有最大层间位移角明显。
(2)最大层间位移角和最大残余层间位移角均受结构基本自振周期影响明显,同一地震动强度水平下,两者均随结构基本自振周期的增大而增大。相比最大层间位移角,最大残余层间位移角的增长速度更快。
(3)随着结构屈服后刚度比的增大和下降段刚度比绝对值的增大,最大残余层间位移角也增大,其离散性也随之变大。

图12 最大层间位移角和最大残余层间位移角的相关系数分布Fig.12 Correlation coefficient distribution of maximum inter-story drift and maximum residual inter-story drift
(4)结构下部楼层的最大残余层间位移角和最大层间位移角的相关性较好,随着楼层上移,两者的相关性趋弱。

