论健康与内生经济增长
龙益楠
(武汉大学经济与管理学院 湖北 武汉 430072)
一、引言
在经济发展中,要做到基础设施建设、健康投资和环境治理有机结合,相互协调,共同促进经济发展。本文即是从这一观点出发,在Barro(1990)内生增长模型的基础上,引入健康资本与环境,分析环境污染治理、健康影响经济增长的机制,并探讨基础设施建设、健康投资和环境治理的联系与分配问题,从而为经济、环境与健康和谐发展提供一个新的视角。
本文的结构安排如下:第二部分对已有的相关文献进行一个简短的回顾;第三部分建立了包含环境与健康的内生增长模型;第四部分分析该模型的动态均衡性质;第五部分结合中国的数据,对模型结果进行数值模拟,并对参数进行敏感性分析;最后对全文进行总结。
二、文献回顾
环境,健康与经济的关系一直是经济学研究的热点话题,实证研究表明环境和健康之前的确存在着密切关系。如环境污染的降低能显著降低婴儿死亡率(Currie&Neidell,2005),改善早产率和低出生体重问题(Currie&Walker,2011),降低儿童急性呼吸疾病发生率(Simeonova et al,2018)。基于这些事实,许多理论研究通过健康作为纽带,将环境与经济联系起来,以此研究环境政策与经济之间的关系。
其中一类研究在Blanchard(1985)世代交叠模型的基础上,引入环境与健康来分析治理环境与经济发展的关系。祁毓和卢洪友(2015)以产出是否依赖于环境质量为标准将生产部门分为两类,发现有污染导致的环境质量恶化将扩大收入不平等。陈素梅和何凌云(2017)研究了能源税收入在居民福利与减排活动之间的分配。
另一类在内生增长模型中将环境、健康做为流量变量或存量变量引入,来分析动态均衡。Agenor(2008)对Barro(1990)进行拓展,引入了生产性的健康支出,但没有考虑环境与经济增长的关系。Gupta&Barman(2010)进一步拓展,将环境质量直接纳入生产函数中,但没有考虑健康与环境的相互关系。黄茂兴和林寿富(2013)基于Romer(1990)模型,将环境作为一种特殊的生产要素,构建了考虑污染损害、环境管理等要素的五部门内生增长模型,但没有考虑环境与健康人力资本间的关系。
据了解,国内在环境、健康与经济的研究主要集中在长期均衡的研究上,只有少数文献基于内生增长模型完整地考虑环境、健康与经济的协调关系,如文建东和花福秀(2016),其重点放在公路、铁路基础设施与死亡率的实证研究上,对内生增长模型的性质没有进一步的讨论。本文在Barro(1990)内生增长模型的基础上,以健康作为环境影响经济的渠道,系统性地分析健康投资、基础设施建设与环境治理间的关系。
三、理论模型
考虑一个人口恒定的经济体和一个无限期存活的代表性家庭,生产和消费一种商品。
(一)生产
经济中的唯一生产部门使用物质资本、劳动力、健康资本和公共基础设施投入作为产品所需投入。在零人口增长的情况下,将人口数标准化为1。假设技术是Cobb-Douglas形,即:
(1)
其中,Y是产出水平,GI是公共基础设施投入,H是健康资本,K是物质资本。α,β和(1-α-β)分别表示公共基础设施,健康资本和物质资本在生产过程中总投入的份额,即产出弹性。
(二)家庭
假定瞬时效用是消费水平C的凹函数,σ表示边际效用关于消费的常弹性:
(2)
家庭将税后收入在消费C和储蓄(投资)间进行分配。物质资本的折旧率假设为0。τ是政府征收的收入税率:
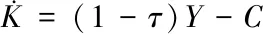
(3)
(三)环境与健康
环境质量随时间的改变取决于污染排放强度(δ是排放-产出系数)和治理行动TY(T为治理支出与收入的比率):

(4)
健康资本由政府的公共健康支出GH和环境质量E组成:
(5)
(四)政府
政府对代表性家庭征收收入税,且这是唯一税收来源。政府将税收收入同时分配到公共基础设施支出GI,治理支出TY和公共健康支出GH中。
GH+GI=(τ-T)Y
(6)
Gi=vi=(τ-T)Y,i=H,I
(7)
式(6)表示政府总支出等于总税收收入。除去环境治理支出的税收分别按比例vH和vI分配到公共基础设施支出GI和公共健康支出GH。因此vi≥0且vH+vI=1。
四、动态均衡
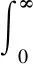
(8)
λ的最优时间路径和消费的增长率分别满足:
(9)
(10)
在平衡增长均衡下,所有的宏观经济变量都以相同的速率gm增长。即:
(11)
(一)唯一平衡增长均衡的存在性
在平衡增长均衡下,所有的宏观经济变量都以相同的速率gm增长:
(12)
(13)
(14)
根据式(12)-(14)得到关于gm的一个等式:
(15)
在满足0<δ 当δ=0时,可得τ*=(α+β),这与Agenor(2008)在只考虑健康资本而没有考虑环境的情况下的结果相一致。所以当我们考虑生产所带来的环境污染问题时,税率会有所提高且提高的程度与排放系数δ成正比。除此之外我们可以发现最优税率并不取决于健康部门的“技术”μ。虽然这一结果是依赖于规模报酬不变这一假定,但也直观地说明从最大化增长率的角度看,重要的是健康对劳动生产力的直接影响。 为了确保增长率非负,政府需要中和由污染引起的环境质量恶化,采取的方式是将δ比率的总产出分配到环境治理中。那么(T*-δ)表示最优净治理支出率,而(1-δ)β(1-μ)表示环境质量在最终产品部门的绿色(不产生污染)产出份额。因此该净最优率等于环境质量的绿色产出份额。类似地,最优总公共支出比率(τ*-T*)等于公共基础设施和公共健康支出的绿色产出份额之和(α+βμ)(1-δ)。该最优比率随污染排放系数反向变动,随公共健康支出的健康资本份额正向变动。 首先定义下列比率变量:x=C/K;y=E/K. 动态系统的移动方程为: 随着资本丰裕度的上升,其产出弹性在长期有着下降的趋势,因此本文借鉴汪伟(2012)的做法,基本情形下资本中国资本的产出份额为(1-α-β)=0.4;在环境污染物中我们选取废气中的烟(粉尘)作为目标污染物,根据《中国统计年鉴2017》,2016年全国废气中烟(粉尘)排放量达到1010.66万吨,GDP为744127.2亿元,计算可得平均每亿元产出排放0.0014万吨污染物,故设污染排放系数δ=0.0014。在环境质量对劳动生产率的影响上,参考陈素梅和何凌云(2017)的做法,假设大气中的污染物是均匀分布的,污染浓度上升1个百分点会使得劳动生产率下降0.09个百分点,即βμ=0.09。而在健康部门的“技术”中,我们假设基本情况下环境质量和公共健康支出同等重要,即μ=0.5。 在现实情况中,由于各方面复杂因素的影响,税收政策的制定是十分谨慎的。因此税率τ本身的数值大小并不具备实际意义,我们主要关心和研究的是税收收入中用于进行环境治理的支出比率,即(T/τ)。我们另一个关注的值是总公共支出中公共基础设施支出所占比率,即vI。由上述参数,我们可以得到T/τ=15.20%,vI=82.35%。从数值模拟结果来看,社会发展的核心(84.80%)依然是公共支出推动经济发展,同时也应注意环境治理工作的实施,来确保均衡发展。而在公共支出的方向及比重选择上,即要重视公共基础设施建设(82.35%),如电力、交通运输等,也要推动公共健康投资。 接下来我们在表1参数取值的基础上,与以往研究对关键参数的赋值及经济体的发展趋势相结合进行参数的敏感性检验。基础情况下只考虑了烟尘的排放量,因此实际环境污染系数可能高于设定值;而近年来党和政府大力推进生态文明建设,“绿色经济”日益成为被关注的热点,越来越多的企业开始研发绿色生产技术,未来排放系数很可能下降。因此考虑排放系数为0.001和0.002两种情况。在健康的形成过程中,很难找到可靠的证据表明环境质量和公共健康支出的相对重要性,因此考虑μ=0.4和μ=0.6两种情况。对于资本产出份额,一些文献估计的资本产出弹性为0.5,白重恩和张琼(2014)发现2008年金融危机后中国资本回报率大幅下降。因此考虑资本产出份额为0.5和0.38两种情况。上述敏感性检验的结果见下表1。 表1 参数取值的敏感性检验 从敏感性检验的结果看来,随着关键参数的变动,环境治理支出在税收收入中所占比重大致上在15%左右,只有当健康“技术”μ发生变化时才有较大波动,但依然处在10%-22%这一较小范围内。而公共基础设施支出在总公共支出占比始终在80%左右轻微浮动,可见基础情形的结论是具有稳健性的。 本文在内生增长的模型的框架下引入健康资本和环境,环境通过影响健康而间接对产出造成影响,研究公共基础设施建设、公共健康投资和环境治理三者间的关系。通过环境对健康的影响,即使在健康是流量变量的情况下,平衡增长均衡依然呈现出转移动态性质且为鞍点均衡。数值模拟结果表明,政府应将工作的核心放在公共支出对经济发展的推动上;同时也应注意环境治理工作的实施来确保均衡发展。而在公共支出的方向及比重选择上,重点在于像电力、交通运输一类的公共基础设施建设,也要推动公共健康投资,不能忽视健康在经济发展中的作用。(二)最优财政政策

(三)转移动态
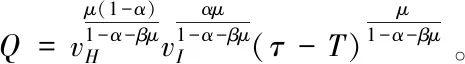
五、数值模拟

六、结论

