基于复杂网络的时间序列转换算法*

何茂雨，周 银，周静曦，沈 黎

(湖南农业大学信息与智能科学技术学院，湖南 长沙 410128)

复杂网络是具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络[1].现实生活中，大量真实的系统如互联网和电网等，都可以抽象成复杂网络，所以复杂网络已经成为学术界热门的研究领域.时间序列是指，将同一统计指标的数值按其发生的时间先后顺序排列而成的数列.时间序列存在于生产、生活的方方面面，如某地区的降雨量、某股票的交易情况、某物品的销售数量等.时间序列分析就是发现时间序列的变化规律并用于预测的统计技术，常见的时间序列分析法有频域分析、时域分析、模型分析和回归分析等.近年出现很多将时间序列转换成复杂网络后，利用复杂网络的特性间接分析时间序列特征的方法.例如，Lucas等[2]提出的可视图算法，田甜等[3]提出的基于频域复杂网络分解的局部特征提取建网方法，李姝等[4]提出的基于随机图的复杂网络建网方法.在经典可视图算法中，需要处理每个时间点对的可视情况，但是在实际情况中，绝大多数的点对都是互相不可视的，所以经典算法中存在大量无意义的计算，有必要对其进行改进.笔者拟引入最大值分裂算法和凸包发现算法来提升经典可视图算法的运行效率.

1 经典可视图算法

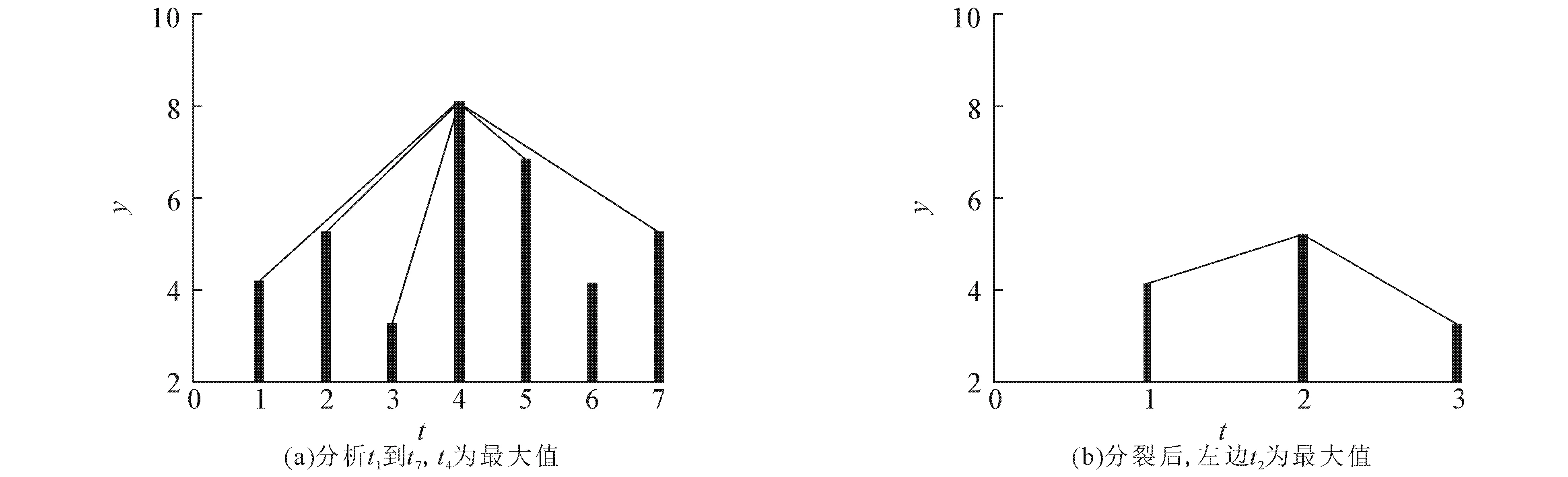
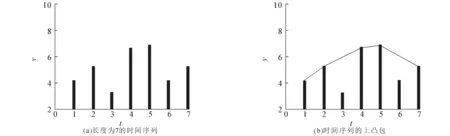
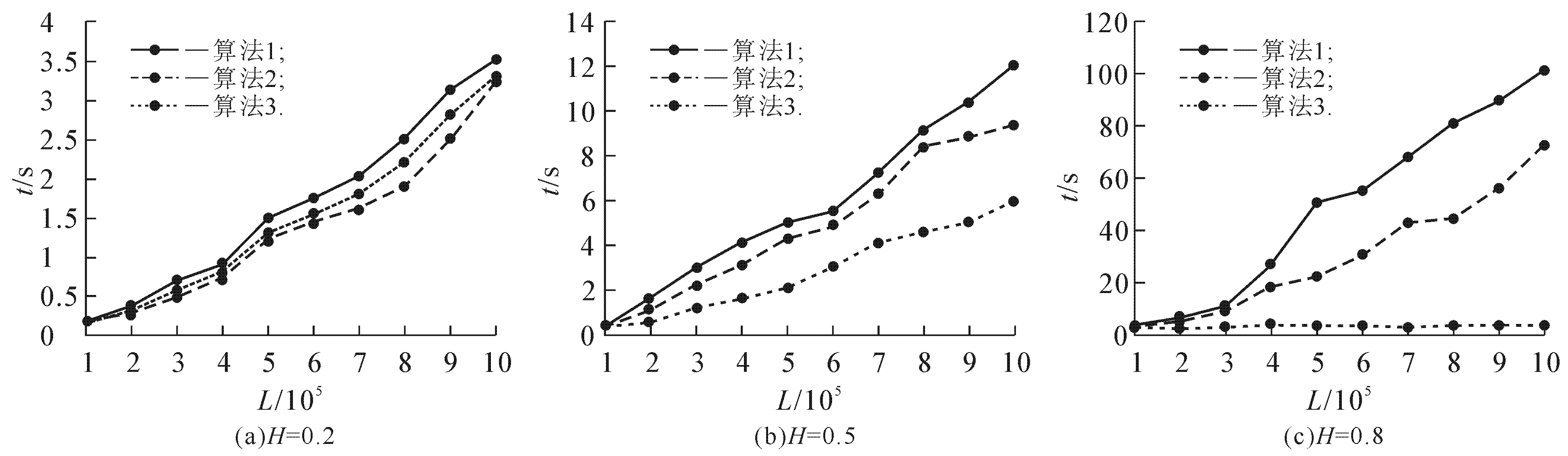
在众多时间序列映射成复杂网络的算法中，可视图算法是较新颖的一种.在离散的时间序列中，每个数据点被看作是网络中的一个节点，数据点之间若满足“相互可视”，则网络中对应的节点之间连线.对于任意2个数据点(ta,ya)和(tb,yb)(假定ta

经典可视图算法描述如下：

(ⅰ)初始化网络，将时间序列中的所有数据点添加到网络中；

(ⅱ)从时间序列第1个数据点i开始，定义每个数据点的初始斜率sl为无穷小；

(ⅲ)对于数据点i之后的每个数据点j，计算线段ij的斜率是否大于sl；

(ⅳ)若大于，则在网络中添加(i，j)连边，并将sl的值变为线段ij的值；

(ⅴ)重复步骤(ⅱ)～(ⅳ)，直到整个时间序列的点遍历完成.

从算法中可以看出，该算法的时间复杂度为O(n2).这就意味着，时间序列的数据点个数较多的情况下，生成复杂网络的代价是十分巨大的，因此有必要对经典可视图算法进行改进以提高效率.长度为10的时间序列的转换结果如图1所示.

图1 长度为10的时间序列的转换结果

2 经典可视图算法的改进

2.1 最大值分裂算法

通过观察发现，在时间序列中，最大值时间点的左边的任意点都看不到其右边的任意点，因此最大值的时间点就将时间序列恰好分裂为相互不可视的2个部分.若先求出时间序列的最大值，则其左右两边就是2个完全独立的时间序列，之后再分别对这2个部分求最大值，于是时间序列被分成独立的4个部分.这样继续分裂下去，直到每个小的时间序列长度为1才停止分裂.具体算法描述如下：

(ⅰ)初始化网络，将时间序列中的所有数据点添加到网络中；

(ⅱ)遍历时间序列，找到最大值，将序列分裂为2个部分；

(ⅲ)分别在2个分序列中找到最大值，将序列继续分裂；

(ⅳ)重复上述操作，直至分裂后的序列长度为1，算法终止.

图2为最大值分裂算法的一个简单示例.

图2 最大值分裂算法示例

在长度为7的时间序列中，t4为该时间序列的最大值，那么t4左边的时间点看不见右边的时间点，于是序列被分裂为2个部分.接下来分析t4左边的情况，t2为最大值，t1和t3互不可见.因分裂后的序列只有1个时间点，故分裂终止.然后分析t4右边的序列，t5为最大值，因t5左边没有时间点，而右边有2个时间点，继续分析t6和t7的情况.t7为最大值，因t7左边只有1个时间点，故算法终止.

2.2 凸包发现算法

点集的凸包是计算机图形学中的术语.在一个实数向量空间中，对于给定集合X，所有包含X的凸集的交集被称为X的凸包.即凸包是一个最小凸多边形，满足点集中的所有点或者在多边形边上，或者在其内部.

观察时间序列(图3(a))可注意到，时间序列上的分割点正好将其分成不可视的几个部分.事实上，如果连接所有的分割点，就正好形成了时间序列顶点的上凸包(图3(b)).

图3 长度为7的时间序列的分割点组成凸包的示例

对于求解二维坐标下的凸包，其算法主要有穷举法、分治法、Jarvis步进法和Graham扫描法等，但是这些算法的时间复杂度都较大.因此，引入凸包发现算法[5]，该算法适用于不自交的简单多线段，是使用双端队列存储凸包结果.

凸包发现算法的伪代码如下：

输入：n个顶点的简单多线段P[i]，这里为时间序列的顶点.

空的双端队列D[]，队列的首尾标签为b，t.

算法流程如下：

(ⅰ)将初始3个点P[0]，P[1]和P[2]加入队列D[]，满足队列的首尾都为P[2]，并使得P[0]，P[1]和P[2]为一个逆时针的三角形.

(ⅱ)依次处理i=2以后的每一个点，检查P[i]是否在D内部：

If P[i]在D[b]D[b+1]和D[t-1]D[t]的左侧，则跳过P[i]，处理下一个点

While P[i]在D[b]D[b+1]的右侧，则从D[]中删除D[b]

在D[]的首部插入P[i]

While P[i]在D[t-1]D[t]的右侧，则从D[]中删除D[t]

在D[]的尾部插入P[i]

输出：双端队列D[]就是最后的结果.

在时间序列转换为复杂网络的过程中，首先利用凸包发现算法计算时间序列的凸包，其点集就是时间序列的分割点，然后分别判断分割点与各个相邻区域的可视情况，从而得到相应的复杂网络.

3 实验部分

为了比较经典可视图算法(算法1)、经最大值分裂算法改进的可视图算法(算法2)和经凸包发现算法改进的可视图算法(算法3)的性能，将3个算法应用于经典的分形布朗运动时间序列中进行观察.分形布朗运动是布朗运动的拓展，是不规则扩散和分形随机行走的基础，其时间序列可以利用MATLAB中的内置函数wfbm(H，L)直接获得，其中H为Hurst指数，L为时间序列的长度.将3个算法应用于H=0.2，0.5，0.8,L=106的分形布朗运动时间序列中，进行20次实验后取平均结果，结果如图4所示.

图4 不同时间序列上3种算法的性能比较

从图4可以看出，相对于算法1，算法2和算法3都能够较好地缩短运行时间，提升效率；且随着Hurst指数的增加，算法3的优势更加明显.这主要是因为，算法3是线性时间算法，其时间复杂度为O(n)，故在时间性能上表现更突出.

4 结语

时间序列转换成复杂网络是当前复杂网络研究的热点问题.笔者分别引入最大值分裂算法和凸包发现算法对经典可视图算法进行改进，获得了较好的实验结果.不足的是，仍然存在时间复杂度较高的问题，找到可以大幅降低时间复杂度的转换算法是今后的研究方向.