面向深度神经网络训练的数据差分隐私保护随机梯度下降算法

李 英 贺春林

1(内江职业技术学院信息技术系 四川 内江 641000)2(西华师范大学计算机学院 四川 南充 637002)

0 引 言

深度神经网络算法在诸如图像分类[1]、语言表达[2]和视觉跟踪[3]等工程应用中取得了十分广泛的应用，但其依赖于采用大量训练数据集对神经网络进行训练[4]，而在使用这些训练数据集时首先需要保证不侵犯数据的隐私权限[5]。然而，对于深度神经网络而言，受到隐私保护的数据集作为训练集可能对算法最终运行结果的正确性产生影响[6-7]。因此，如何在运用深度神经网络算法的同时有效保护训练样本数据的隐私不受侵犯显得至关重要。

学者们针对神经网络的训练数据隐私问题进行了相关研究。例如，文献[8]针对含有加密后的数据分析计算问题，提出了基于同态加密技术的机器学习算法，在保证不解密的情况下直接对密文进行计算，并与解密后明文计算结果相同。然而，同态加密技术存在运算效率低的缺点。文献[9]提出了基于Flash排序算法与k-匿名保护算法相结合的分类机器学习算法，实现隐私数据保护的同时保持数据集的最优效用，但k-匿名算法本质上仍存在隐私信息泄露的可能性。

近年来，差分隐私技术被广泛应用于数据私密性保护中，其基本原理为对原始数据通过转换、添加噪声等方法来达到隐私保护的效果，从而确保数据集在执行插入或删除操作时对最终的计算结果不会产生影响。基于此，本文提出一种结合差分隐私的随机梯度下降算法，实现数据隐私保护与神经网络算法的有机结合，主要贡献包括：

(1) 针对传统随机梯度下降算法不考虑对数据隐私性的破坏影响，提出了基于差分隐私保护的随机梯度下降算法，引入附加高斯噪声对数据隐私性进行保护的同时，保证对深度神经网络的训练效果。

(2) 为衡量所提差分隐私随机梯度下降算法对数据隐私的破坏程度，提出隐私损失累积函数的概念对每次迭代过程中的数据隐私破坏程度进行度量。此外，还讨论了算法中关键参数对神经网络训练效果的影响。算例实验表明，所提算法能够有效实现数据隐私保护与算法执行效率间的折中平衡，具有较好的应用前景。

1 相关概念

1.1 基于附加高斯噪声的差分隐私保护机制

差分隐私算法[11]的数学基础为相邻数据集概念，具体的数学定义如下：

定义1对于一个随机映射机制M：D→R，其中D为域，而R为范围满足(ε,δ)为差分隐私的，若其满足对于任意两个响铃输入d,d′∈D和任意输出子集S⊆R有如下不等式成立：

Pr[M(d)∈S]≤eεPr[M(d′)∈S]+δ

(1)

式中：ε为差分隐私预算参数，其表征了隐私保护程度，ε越小表示隐私保护程度越高；而δ则表征了差分隐私被破坏的概率值。由定义1可知，差分隐私技术限制了任意对数据集的操作对算法运行结果的影响。具体操作为：令f表示某一算法，f(d)和f(d′)分别表示两个相邻数据的执行结果。差分隐私即通过调整参数ε来保证对数据集中对同一条数据进行删除或添加操作后输出同一结果的概率控制在eε之内，且差分隐私被破坏的概率小于δ。从上述分析可知，(ε,δ)同样反映了隐私保护的开销程度。此外，文献[12]提出，实现差分隐私的关键在于向数据添加随机噪声，最常见的是添加高斯随机噪声：

(2)

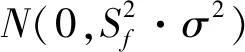
然而，添加噪声的程度与算法对数据的敏感度以及需要控制的隐私保护程度有关。换言之，若加入的噪声程度过大，则算法运行结果的可信度会下降；反之，若加入的噪声程度太小，则无法对数据提供可靠的安全保障。为衡量算法对添加噪声的敏感程度，引入如下定义：

定义2对任意算法f：D→R，算法的全局敏感度GS(f)定义为：

(3)

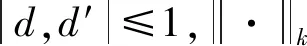
1.2 深度学习

如图1所示，深度神经网络基于模块化思想，通过在多个层次上部署多个神经元并通过逐层训练的手段调整神经元间的连接权值，从而实现原始特征数据进行多次非线性变换，对于任何有限给定输入/输出数据的拟合，最终获取到稳定的特征用于后续的问题分析。

图1 深度神经网络结构图

深度神经网络算法中，为评估所提神经网络输出预测值与真实值之间的差异程度，用损失函数L表示，文中采用均方差损失函数，表示为：

(4)

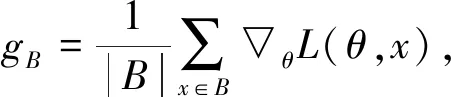
2 基于差分隐私保护的SGD算法

提出一种基于差分隐私保护的随机梯度下降算法。为约束算法迭代过程中对数据隐私性的侵犯，提出隐私损失累积函数的概念对隐私侵犯程度进行度量。

2.1 算法步骤

现有研究中，差分隐私和随机梯度下降算法之间参数的配合选取与交互影响机制尚不明确。例如，在训练数据中加入的噪声过于保守，则在实际算法运行时的准确率将受到影响。因此，通过定义一个数据隐私损失累积函数来量化度量随机梯度下降迭代过程中对数据隐私的侵犯程度。

算法1展示了所提差分隐私SGD算法的基本步骤，其目标函数通过不断训练和调整权重系数θ来最小化损失函数L。其基本思想为：在每次迭代过程中，首先计算随机生成的批量样本的梯度▽θL(θ,xi)，并基于计算生成的梯度值的L2范数进行梯度剪切。随后，考虑到样本数据的隐私保护，基于附加高斯噪声方法以梯度与随机噪声之和的均值对剪切后的梯度进行更新，得到下一步迭代的权重系数θ。最后除最终权重系数之外，还需要输出由于差分隐私保护机制带来的隐私损失。

算法1差分隐私SGD算法

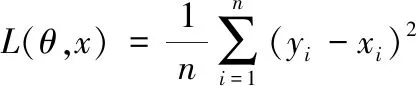
初始化：随机生成权重系数θ0

Fort∈[T]do

输出：θT和使用隐私损失累积函数计算得到的隐私开销(ε,δ)

相关术语解释如下：

神经网络各层参数：神经网络各层参数(即权重系数θ)都作为损失函数L的其中一部分参数。算法1同样表明，对于每一层而言均可以对剪切阈值和噪声程度进行单独设置，且可能随着训练迭代步骤t的增长而变化。

2.2 基于隐私损失累积函数的差分隐私侵犯计算

对于所提差分隐私SGD算法，除了确保算法运行的准确率以外，另一个重要的问题就是评估算法训练时的数据隐私损失成本。为此，提出隐私损失累积函数的概念来进行每次迭代过程访问训练数据的隐私损失以及随着训练进展时的累积隐私损失。

进一步地，对于两个相邻的数据集d,d′∈D和映射机制M，引入一个辅助输入变量aux和输出o∈R，定义映射机制M在输出o处的隐私损失为：

(5)

对于所提差分隐私SGD算法而言，神经网络各层权重系数的参数值与每次迭代过程中的差分隐私机制有着紧密的关联，从而对于给定的映射机制M，在第λ次迭代过程的隐私损失定义为:

(6)

进一步地，映射机制M的损失边界值定义为:

(7)

其满足如下特性:

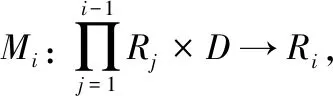
(8)

2) 差分隐私边界：∀ε>0，映射机制M是(ε,δ)差分隐私的，当且仅当:

(9)

上述2条性质确定了深度神经网络算法每次迭代的隐私损失以及所能够达到侵犯数据隐私容忍度的最大迭代次数。特别地，在附加高斯噪声的情况下，不妨令μ0、μ1分别为N(0,σ2)和N(0,σ2)的概率密度函数，而μ为两个高斯密度函数的混合概率密度函数，即μ=(1-q)μ0+qμ1。依据式(5)-式(7)可推导得α(λ)=log max(E1,E2)，其中：

(10)

(11)

隐私损失边界为：

α(λ)≤q2λ(λ+1)/(1-q)σ2+O(q3/σ3)

(12)

3 实 验

3.1 实验步骤

本文算法采用基于数据流编程(dataflow programming,DP)的TensorFlow符号数学系统[15]进行编程。为了保护数据隐私，需在进行梯度下降更新每一层权重系数参数值之前对数据进行清洗。此外，还需根据数据清洗的处理方式计算每次迭代过程中的隐私损失。故算例执行过程中主要包含两大部分：1) 数据清洗，梯度计算前对数据进行清洗以保护隐私；2) 隐私损失累积，在训练过程中计算每次的隐私损失。

算法2和算法3为基于TensorFlow框架下使用Python语言编程的所提差分隐私SGD算法的核心代码片段。其中：算法2为使用所提差分隐私SGD算法对损失函数不断优化，命名为DPSGD_Optimizer；而算法3则为隐私损失累积成本函数进行隐私损失迭代计算，命名为DPtrain。

算法2SGD算法核心代码

class DPSGD_Optimizer():

def_init_(self,accountant,sanitizer):

self_accountant=accoutant

self_sanitizer=sanitizer

def Minimize(self,loss,params,

batch_size,noise_options):

#计算梯度之前的累计隐私损失

priv_accum_op=

self._accountant.AccumulatePrivacySpending(

batch_size,noise_options)

with tf.control_dependencies(priv_accum_op):

#计算每个样本的梯度

px_grads=per_example_gradients(loss,params)

#数据清洗

sanitized_grads=self._sanitizer.Sanitize(

px_grads,noise_options)

#执行梯度下降操作

return apply_gradients(params,sanitized_grads)

算法3 隐私损失累积函数代码

def DPTrain(loss,params,batch_size,noise_options):

accountant=PrivacyAccountant()

sanitizer=Sanitizer()

dp_opt=DPSGD_Optimizer(accountant,sanitizer)

sgd_op=dp_opt.Minimize(

loss,params,batch_size,noise_options)

eps,delta=(0,0)

#在预定义的隐私损失限值内输出训练结果

while within_limit(eps,delta):

sgd_op.run()

eps,delta=accountant.GetSpentPrivacy()

多数情形下，神经网络模型可通过基于主成分分析(principal component analysis,PCA)将输入投影在主方向上或通过卷积层反馈的方式来提高训练效率与训练效果。同样地，算例中也使用差分隐私+PCA的方案在公共数据上进行神经网络卷积层的预训练。

3.1.1数据清洗操作

为实现对样本数据的隐私保护，数据清洗操作需要执行两项操作：1) 通过裁剪每个样本的梯度范数来限制样本中每个数据对最终生成梯度的影响；2) 在更新神经网络各层权重系数参数值之前，将随机噪声添加至批处理的梯度中。

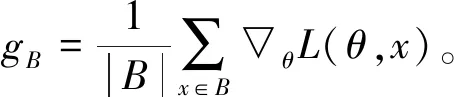
3.1.2隐私损失累积函数的主成分分析操作

进行隐私损失累积操作的主要目的在于跟踪计算每次训练迭代过程中的隐私损失成本。如第2节所述，可以根据所加噪声的分布参数进而确定每次叠加过程的隐私损失α(λ)。

此外，由于主成分分析(PCA)是捕获输入数据主要特征的有效方法。对于用于训练神经网络的随机样本，将其视为向量并进行L2范数归一化处理，形成对称矩阵(记为A)，其中每个向量是矩阵A中的一行,并基于所提附加高斯噪声的方法添加到协方差矩阵ATA，并计算噪声协方差矩阵的主方向。最终将每个输入的训练样本投影到主方向上作为神经网络最终的输入数据。

3.2 典型数据集验证与结果分析

为验证所提基于差分隐私的SGD算法的可行性与优异性，采用两个流行的图像数据集MNIST[17]和CIFAR-10数据集[18]对算法进行验证。此外，采用文献[19]所提无差分隐私的常规SGD算法作为对比算法。

3.2.1MNIST手写数字识别

MNIST数据集为手写数字识别数据集。首先将样本分为包含60 000幅图片的训练样本和包含10 000幅图片的测试样本。每幅样本均为28×28的灰度图像。神经网络采用前馈架构并具有ReLU激活函数以及10类的Softmax分类器。

(1) 差分隐私基准实验。选择PCA投影层维度为60维，包含1层具有1 000个ReLU激活单元的隐含层，并将Lot样本规模设置为600，设梯度剪切阈值为4。复杂的高斯噪声强度分为三类：小强度噪声(σ=2,σp=4)，中等强度噪声(σ=4,σp=7)和大强度噪声(σ=8,σp=16)。其中：σ为训练神经网络时选择的附加噪声标准差；σp为PCA投影时的噪声标准差。初始学习率设置为0.1，并在10个Epoch内线性地递减至0.052并在今后的训练过程中内保持不变(1个Epoch等于使用训练集内样本全部训练一次)。

采用固定变量法进行验证。首先令δ=10-5并保持不变，图2为不同噪声级别下神经网络算法对手写数字识别准确率随着训练次数以及差分隐私预算参数ε的变化情形。可以看出，训练完成后的神经网络在(0.5,10-5)-差分隐私、(2,10-5)-差分隐私和(8,10-5)-差分隐私水平下的准确率分别超过了90%、95%和97%，且训练集和测试集的识别准确率结果相差不大。反之，采用非差分隐私的SGD算法进行训练时，训练集和测试集的准确率差距则存在过度拟合的现象，即随着Epoch数量的增加，二者差距逐渐增大。此外，非差分隐私的SGD算法最终的测试准确度较所提算法虽然在大强度噪声情况下较为接近，但在中等强度噪声和低强度噪声时则比本文算法分别低6.2%和9.7%，这进一步说明本文算法具有更好的辨识性能。

(a) 大强度噪声

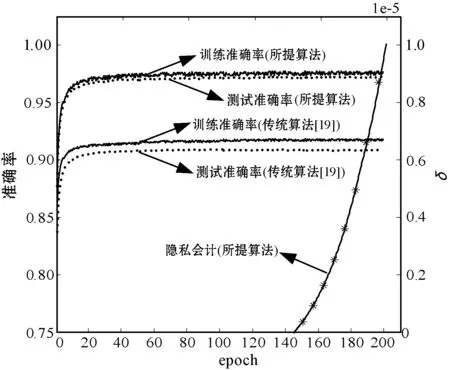
(b) 中等强度噪声

(c) 低强度噪声图2 MNIST数据集辨识准确度随噪声变化的趋势

(2) 相关参数对算法性能的影响。进一步研究所提差分隐私SGD算法中相关参数对算法性能的影响。算法参数包括PCA维度数量、隐含层激活单元的数量以及相关训练参数(如Lot样本规模、学习速率、梯度范数剪切阈值和噪声强度等)。与差分隐私基准实验类似，同样通过固定变量方法研究上述参数对算法性能的影响，即在其余参数不变的情形下单独研究某一参数对算法性能的动态影响。实验过程的基准参数同样采用3.1.2节中所述参数值。

PCA维度数量：图3(a)为辨识准确度随着PCA维度数量的变化趋势。无PCA和随机映射方法下准确率始终保持不变，而所提方法的辨识准确度随着映射维度的变化而发生波动，但总体上的辨识准确率优于前述两种方法。

隐含层激活单元的数量：图3(b)为辨识准确度随着隐含层激活单元数量的变化趋势。可知，对于常规的非差分隐私SGD算法而言，只要选择合理的手段来避免过度拟合，则准确率随着激活单元数量的增多而逐渐提升。但对于所提差分隐私SGD算法，激活单元数量的增多并不能必然保证准确率的提升，这是因为增多的激活单元增加了对梯度灵敏度的影响，从而导致在梯度更新时需要添加额外的随机噪声。此外还可得到另一结论是，对于所提差分隐私SGD算法，并不需要通过一味地使用非常大的神经网络也能得到令人满意的算法性能。

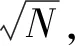
学习率：图3(d)为学习率对辨识准确度的影响。可见，当学习率维持在[0.01,0.07]且终值为0.05时，准确率保持稳定。若学习率过大，则准确度会显著下降。

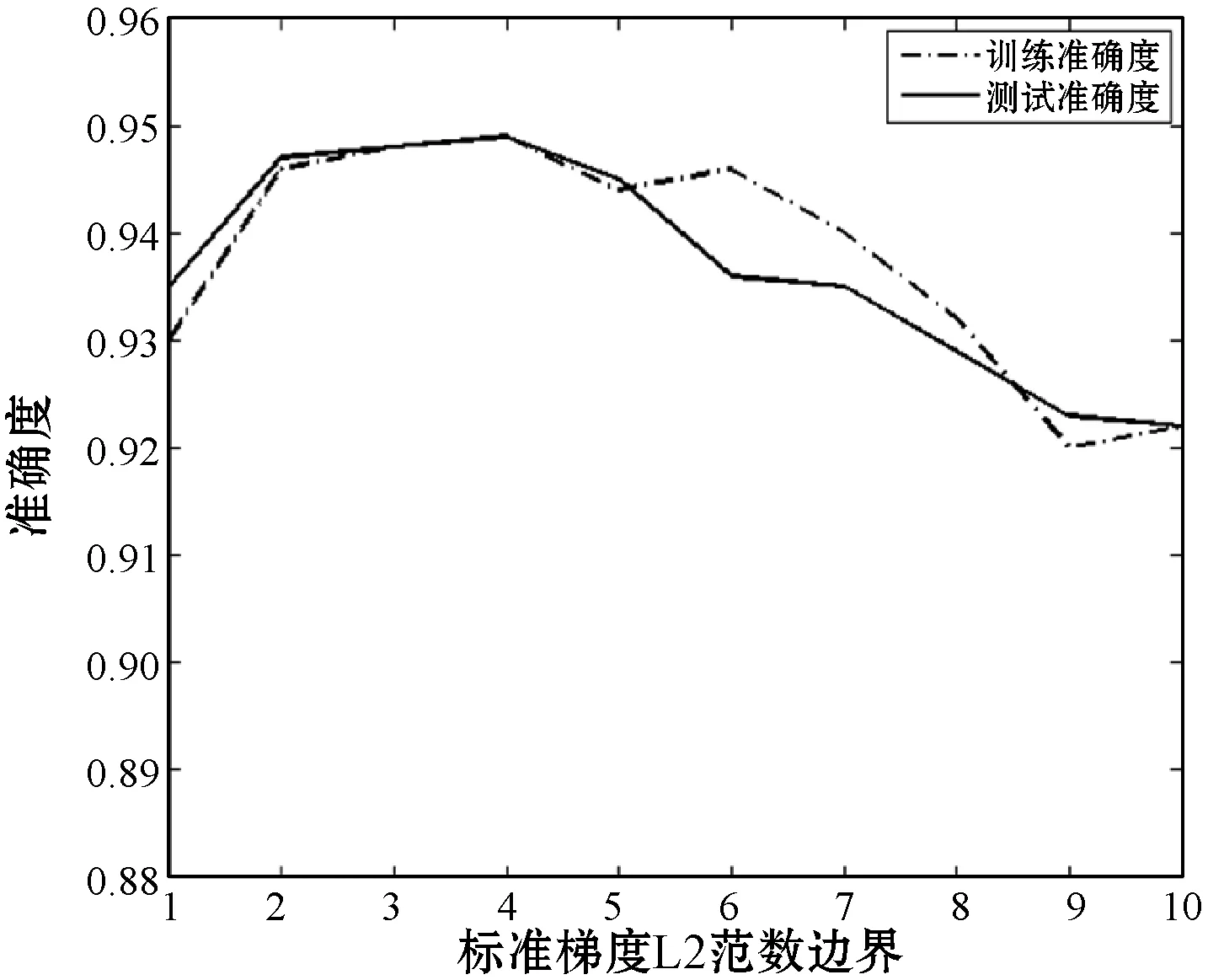
梯度范数剪切阈值：图3(e)为梯度范式剪切阈值对辨识准确率的影响。当剪切阈值在[2,5]时辨识准确率基本保持稳定，而阈值超过5后，辨识准确率出现了明显的下降。这是由于梯度范数剪切阈值的选取需要综合考虑如下两个因素：1) 若阈值取值过小，则最终以平均值代替真实梯度时可能造成误差过大；2) 若阈值取值过大，则由算法1可知，将会导致最终根性的梯度中注入过多的噪声。

噪声强度：图3(f)为附加高斯噪声强度对最终辨识准确率的影响。当σ取[3,4]时辨识准确率达到最优，而超过这一范围的σ，其辨识准确率出现了急剧的下降，这表明噪声强度的选取对最终准确率有着至关重要的影响。

(a) 映射维度变化

(b) 隐藏单元变化

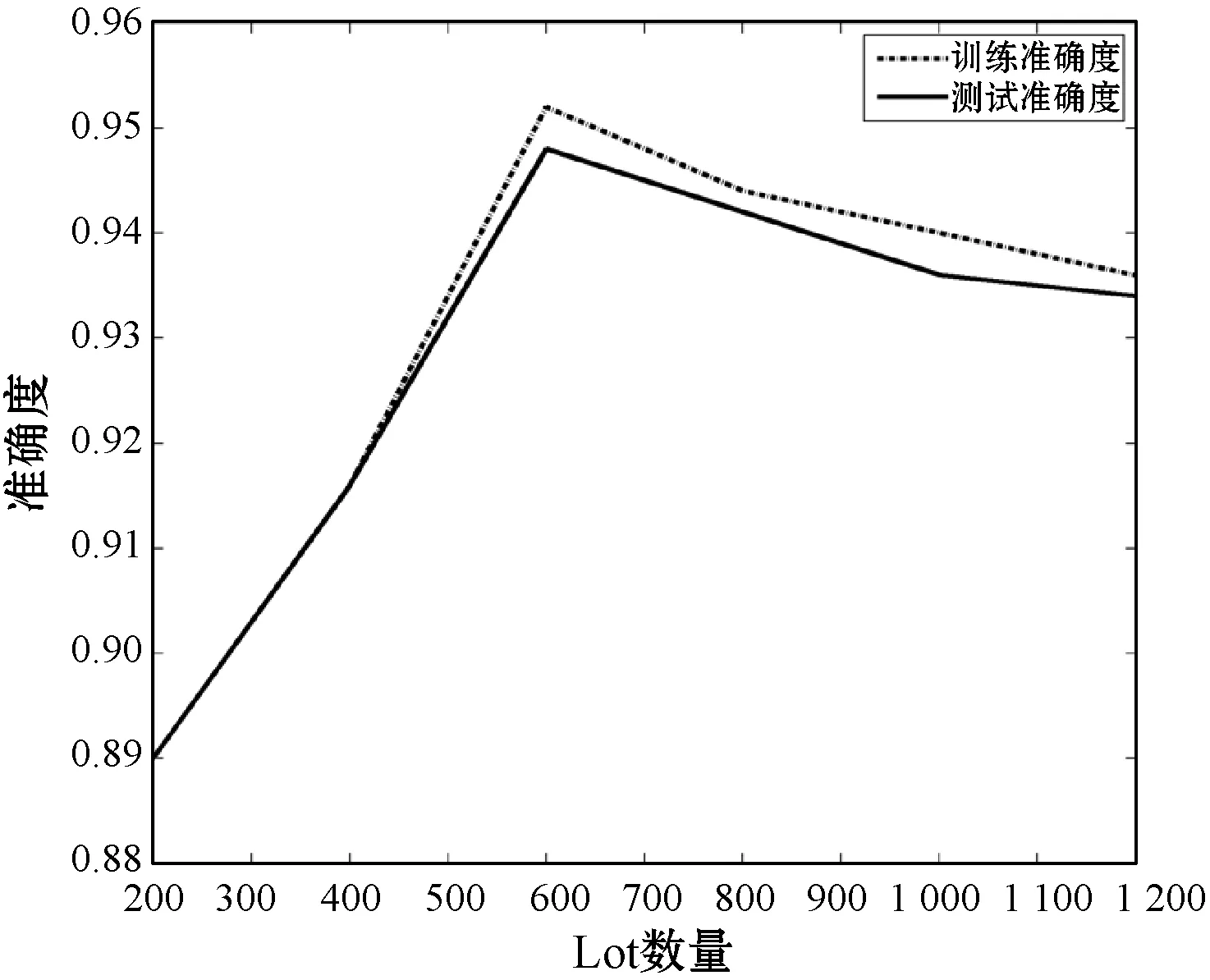
(c) Lot数量变化

(d) 学习率变化

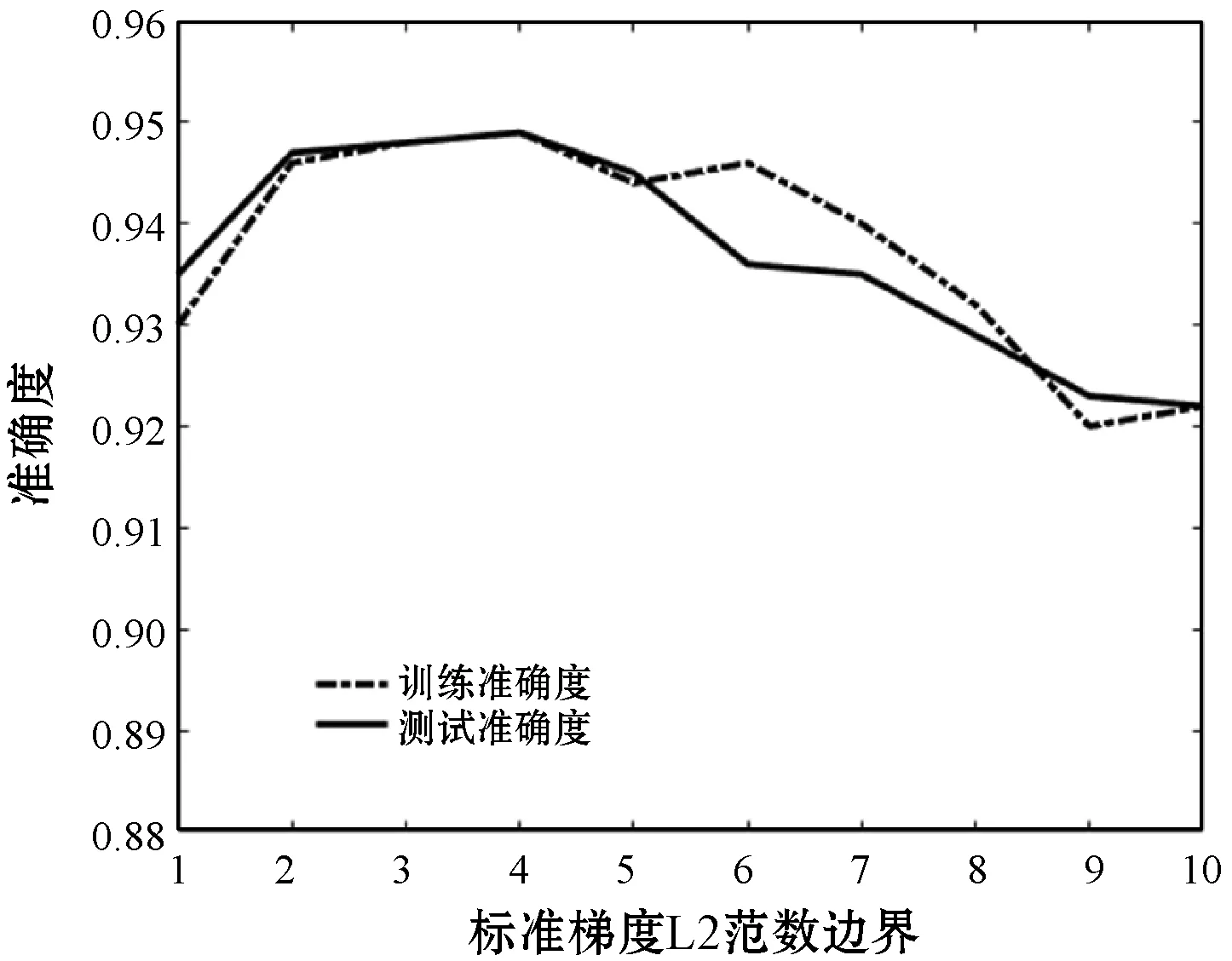
(e) 梯度剪切范数变化

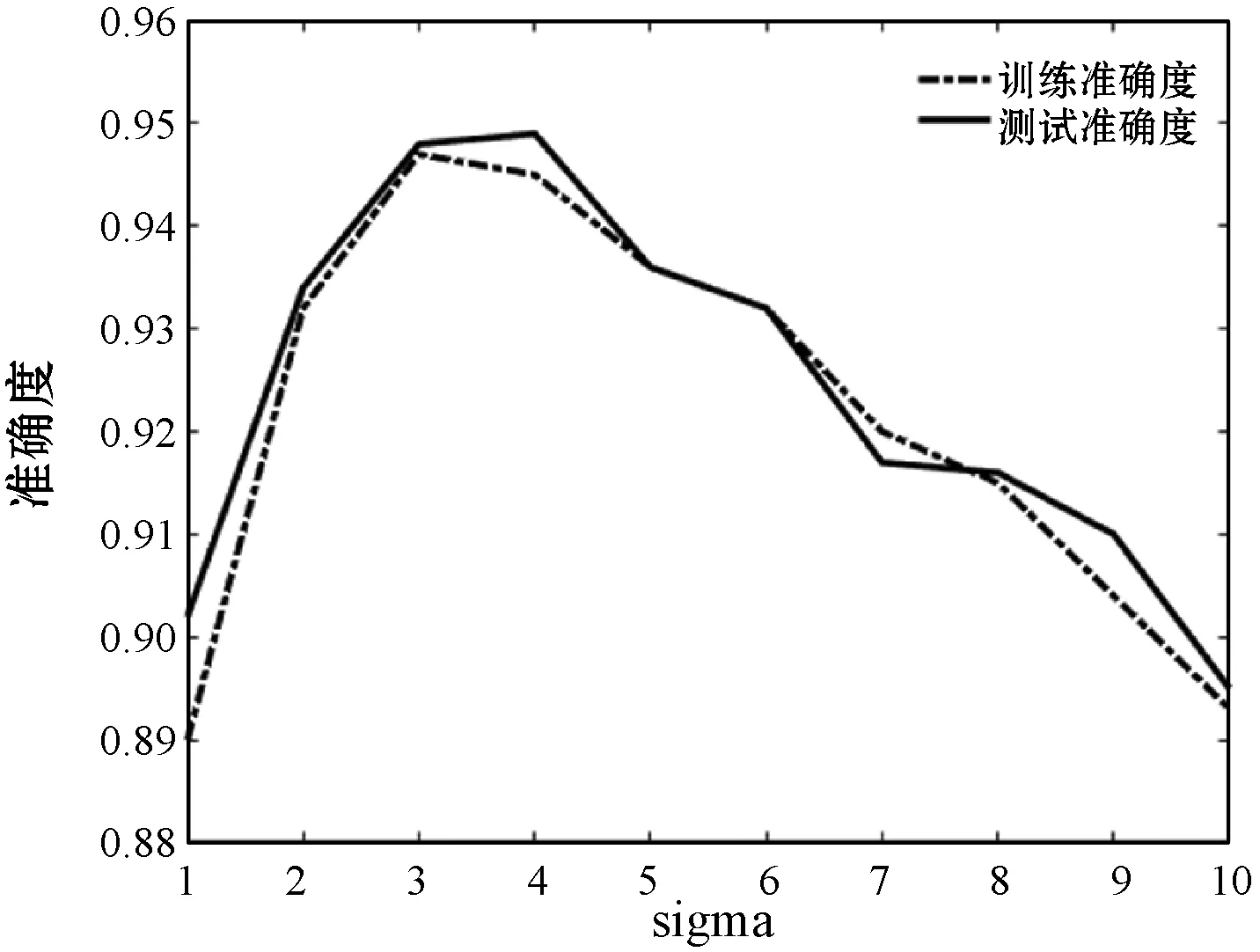
(f) 噪声强度变化图3 MNIST数据集辨识准确度随参数变化趋势

综上，对于MNIST数据集验证实验，可得到如下结论：

1) PCA提高了模型精度和训练性能。但PCA维度的选择对最终的辨识准确度没有明显的影响。

2) 隐含层激活单元数量对最终的辨识精度没有明显的影响，对于一个复杂求解问题而言，应用本文方法可以通过运行较小的神经网络来达到令人满意的效果。

3) 学习率、Lot样本规模和噪声强度对深度神经网络求解性能有着很大的影响。本文中仅通过人工经验选取的方法来确定，后续可进一步通过研究自适应参数选择方法来确定这类关键参数。

3.2.2CIFAR-10图像分类

为进一步说明所提差分隐私SGD算法的通用性，使用CIFAR-10图像数据集进行验证。其中，数据集由10类包含人类、交通工具和动物组成，选择50 000个样本用作训练而10 000个样本用作测试。

算法采用TensorFlow中卷积神经网络的示例网络架构。算例使用两级神经网络，附加高斯噪声参数σ=6，梯度范数剪切阈值选择为3，Lot样本规模选择为2 000和4 000。图4为分类准确度和隐私成本随着训练过程变化的趋势。其中，(a)-(c)对应ε=2,4，6，而Lot样本规模则分别为2 000、4 000和4 000。与2.2节类似，训练样本和测试样本的准确率较为接近，分别约为67%、70%和73%。可见，本文方法对图片分类较高的准确率，适用性强。

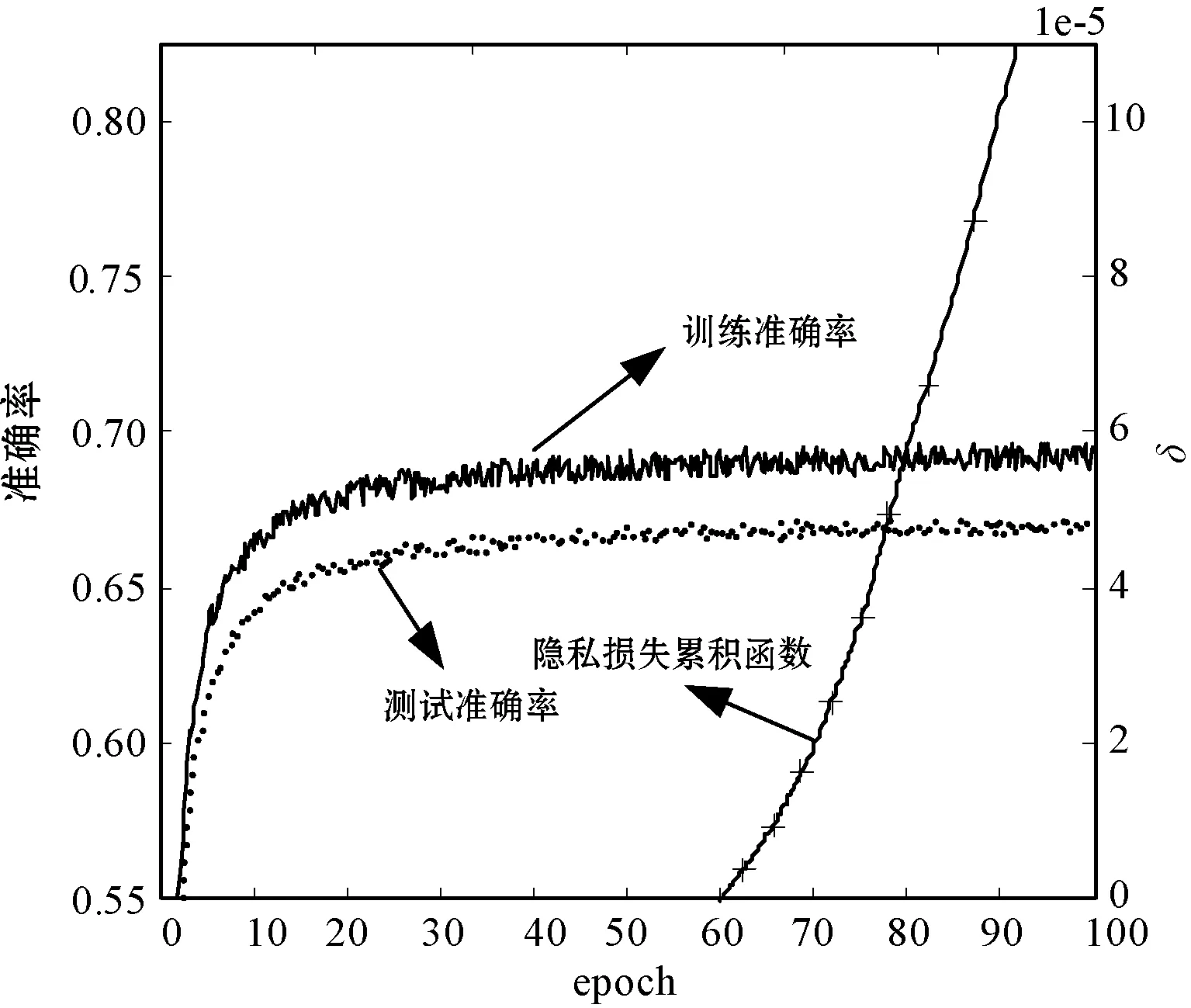
(a) 大强度噪声

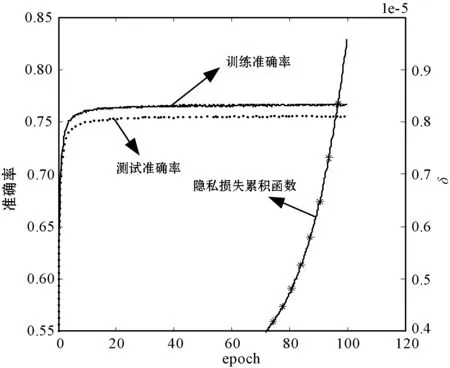
(b) 中等强度噪声

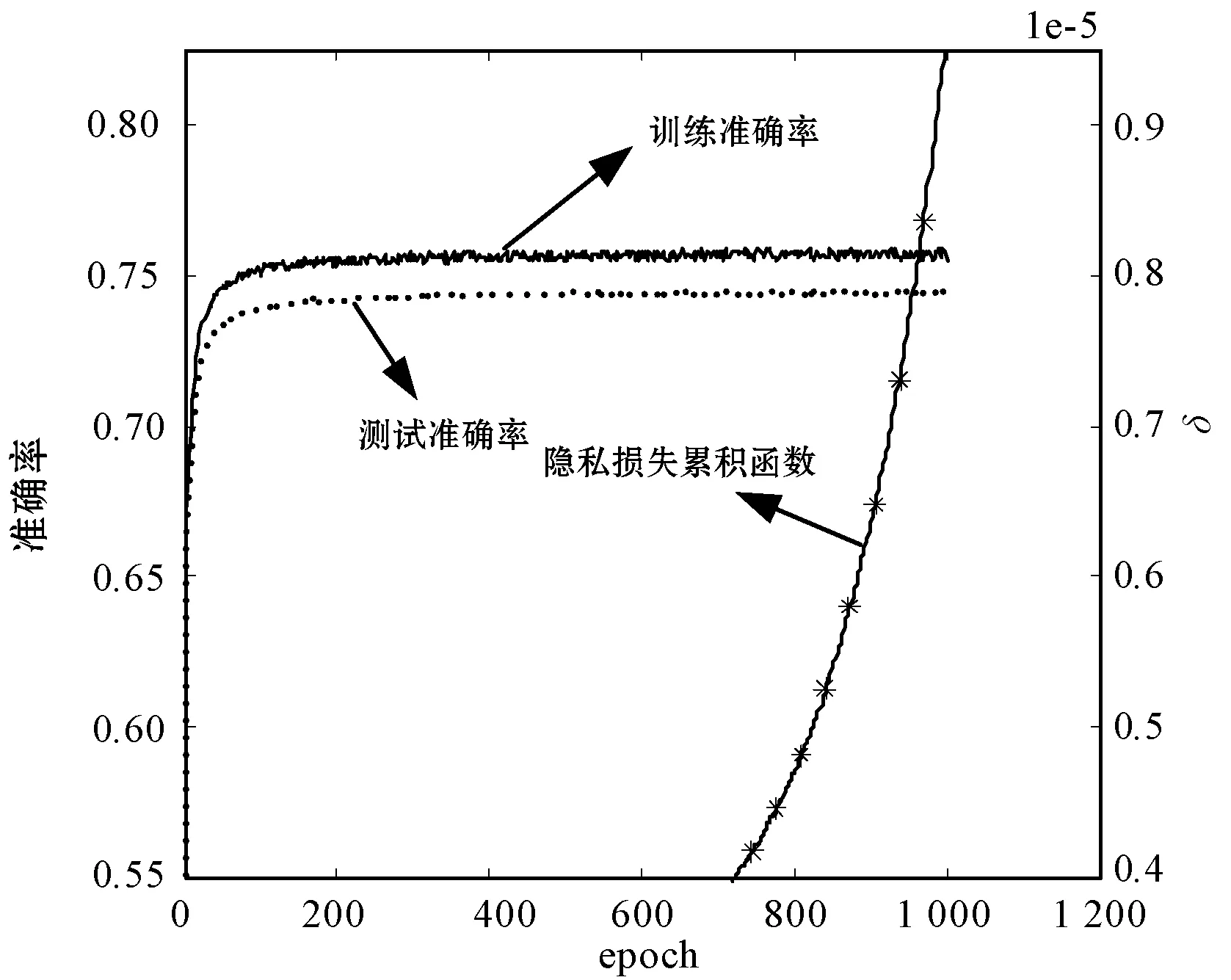
(c) 低强度噪声图4 CIFAR-10数据集辨识准确度随噪声变化的影响

4 结 语

为保证深度神经网络训练过程中对训练样本数据的隐私信息的保护，本文提出一种基于差分隐私随机梯度下降算法的深度学习网络算法。MNIST手写数字识别算例和CIFAR-10图像分类实验表明，本文算法的辨识准确度分别达到了90%和70%的同时，有效保护了数据的隐私性。结果表明，本文算法的适用范围广，并在辨识准确度以及数据隐私性方面取得了较好的折中平衡。未来将进一步研究对差分隐私-SGD算法参数的自适应选取策略以及辨识准确度，进一步提升策略。