地震波斜入射下层状TI饱和场地地震反应分析

巴振宁 ，张家玮 ，梁建文 ，吴孟桃

(1.中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学)，天津 300350；2.滨海土木工程结构与安全教育部重点实验室，天津300350；3.天津大学土木工程系，天津 300350)

场地自由场地震反应是研究地震波散射和土-结构动力相互作用的基础[1－2]，因此，该课题一直是岩土工程、地震工程和地震学等领域研究的重点。目前，国内外学者针对弹性波在不同介质中的传播问题已开展了较多研究。对于各向同性弹性介质，Haskell[3]和 Thomson[4]最先给出了层状介质中波传播问题的传递矩阵解；随后Kausel和Roësset[5]采用Haskell-Thomson传递矩阵的方法进一步推导了层状半空间动力刚度矩阵，并通过改变波型和控制点的位置，用刚度矩阵方法研究了层状弹性半空间场地竖直和水平运动分量变化对自由场的影响；Wolf和Obernhuber[6]推导了层状半空间精确动力刚度矩阵，并采用刚度矩阵的方法求解了不同波入射时层状半空间时的动力响应；于国友等[7]应用Haskell-Thomson传递矩阵方法，给出了不同性质场地对地震波的放大作用曲线；梁建文和巴振宁[8]将Wolf动力刚度矩阵推广至三维，分析了基岩上单一土层场地的动力响应。对于各向同性饱和多孔介质，Deresiewicz和Rice[9]推导了含粘性液体饱和多孔介质 Biot动力平衡方程的通解，并给出了相速度、衰减系数、反射角和振幅比的解析表达式；Deresiewicz[10]推导了含有液体的多孔半空间中表面波的速度衰减系数表达式；Yang和 Sato[11]基于Biot两相介质理论，模拟了饱和场地的地震反应，分析了饱和效应对单土层竖向地震激励的影响；Lin[12]研究了孔隙率、固结状态、边界排水等多种因素对无粘流体饱和多孔半空间动力响应的影响；李伟华等[13]应用显式有限元方法，分析了含有饱和软弱土层场地的动力响应；巴振宁和梁建文[14]在频域内求解了流体饱和半空间中埋置球面波源(球面膨胀P1和P2波源以及剪切SV波源)的动力响应。

值得指出的是，上述研究均基于各向同性介质(弹性或饱和)的假定。然而，天然土体具有固有各向异性和应力各向异性已逐渐成为岩土工程界的一种共识。由于风化沉积作用，天然土体的水平弹性模量往往大于其竖直弹性模量[15]，因此，采用横观各向同性(transversely isotropic，简称 TI)介质力学模型来描述土体的各向异性更为合理。对于弹性波在TI介质的传播问题，陈镕等[15]建立了层状TI场地模型，利用刚度矩阵的方法计算了其动力响应；薛松涛等[16]分析了 TI场地在三种不同底部边界条件下的动力响应。基于 Biot两相介质理论，Schmitt[17]推导了柱坐标系下 TI饱和介质的波动方程，研究了柱面波的频散和衰减曲线及与参数相关的灵敏度系数；Sharma[18]推导了直角坐标系下平面谐波的特征方程，并给出了三种准波波速的解析表达式；Liu等[19]考虑了流体粘度，研究了TI饱和多孔介质中的波传播问题；陈胜立和张建民[20]建立TI饱和半空间模型，并给出了受荷载作用时场地的动力响应；陆建飞等[21]建立了轴对称情况下 TI饱和土层的反射、透射矩阵，求解了集中力作用下TI饱和场地的频域响应。然而，目前很少有针对地震波斜入射下TI饱和场地时域响应分析的研究。

本文将Haskell-Thomson传递矩阵方法拓展到层状 TI饱和半空间，通过层间位移、应力连续条件及地表边界条件建立了传递矩阵方程，进而结合快速傅里叶变换，求解了地震波斜入射下层状 TI饱和场地的时域自由场反应。文中通过将退化后场地的计算结果与已有文献结果对比验证了方法的正确性，并进行了不同工况下的计算分析，研究了土体 TI性质及饱和特性对自由场响应的影响，得到了一些有益结论。

1 层状TI饱和半空间模型及其求解

层状TI饱和半空间模型如图1所示。模型中各土层的厚度为dj(j=1,2,…,N)，相对应的土层下表面深度为zj(j=1,2,…,N)。土层和半空间性质由五个工程常数(Eh、Ev、Gv、νh、vvh)和饱和相关参数(m1、m3、α1、α3、k1、k3、η、ϕ)以及质量密度ρ和阻尼比ζ进行描述。设波入射位置在基岩露头，入射方向与竖直方向夹角为θ。

具体求解时：首先，根据 TI饱和多孔介质动力平衡方程及孔隙流体运动方程求得其基本解；然后，根据层间连续条件建立传递矩阵，联立地表边界条件求得各层土中来波和去波的幅值；最后，代入基本解即可得到层状TI饱和半空间自由场响应。

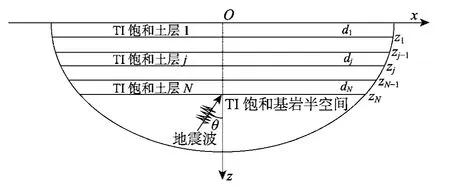
图1 层状TI饱和半空间模型Fig.1 The model of multi-layered TI saturated half-space

1.1 TI饱和多孔介质波动方程及其基本解

根据文献[19]，TI饱和多孔介质平面内应力-应变关系为：

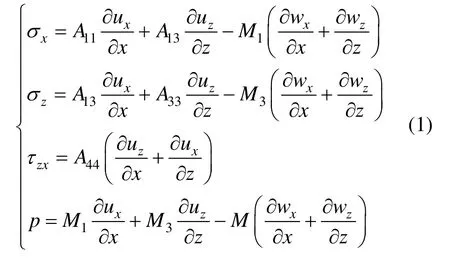
式中：σx、σz、τzx=τxz为总的应力分量；p为孔压；ux和uz为土骨架的位移；wx和wz为流体相对位移；A11、A13、A33、A44和M1、M3均为与两相材料有关的参数，其具体表达详见附录A。

直角坐标系下[22]，以u-w形式表示的Biot动力平衡方程为：

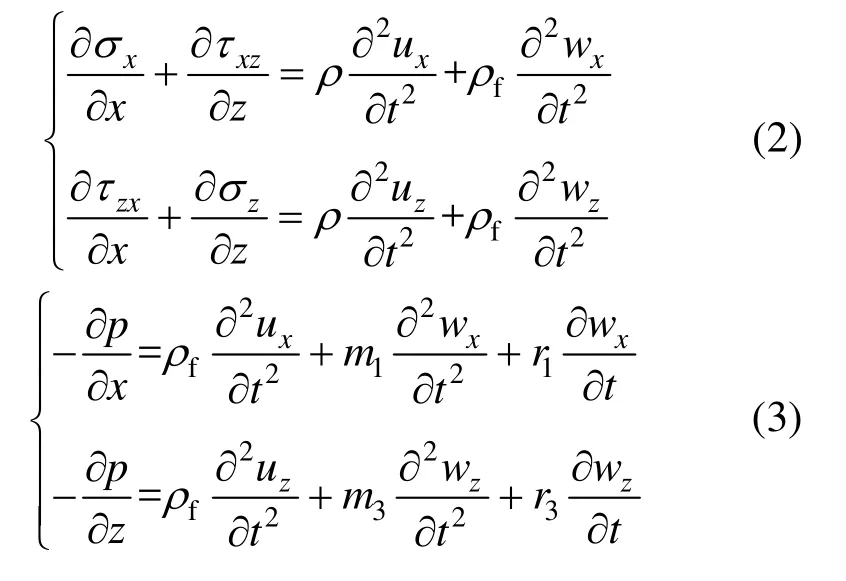
式中：ρm为 TI饱和多孔介质密度ρ=(1-ϕ)ρs+ϕρf，ρs和ρf分别为土体密度和孔隙流体密度；t为时间变量。

讨论简谐弹性波的传播，不失一般性可取解的形式为：

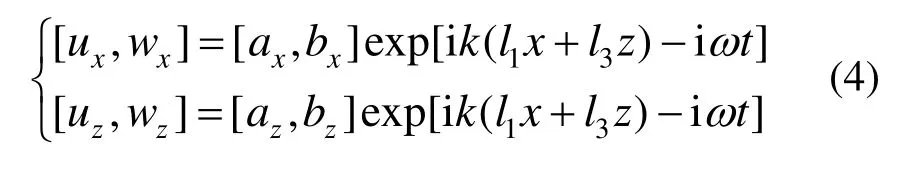
式中：l1=sinθ，l3=cosθ；ax、bx、az和bz为波幅值；k=ω/c为水平波数，ω为振动圆频率，c为视速度。

将式(4)代入式(2)和式(3)并考虑 qP1、qP2和qSV波所引起的位移之间的耦合关系，可得位移表达式如下：

式中：χ1~χ6、δ1~δ6具体表达式详见文献[23]；AqP1、AqP2和AqSV可视为在z轴负向传播的qP1波、qP2波和qSV波的幅值；BqP1、BqP2和BqSV可视为在z轴正向传播的qP1波、qP2波和qSV波的幅值；λqP1、λqP2和λqSV分别对应qP1波、qP2波和qSV波的波数，其具体表达式如下：

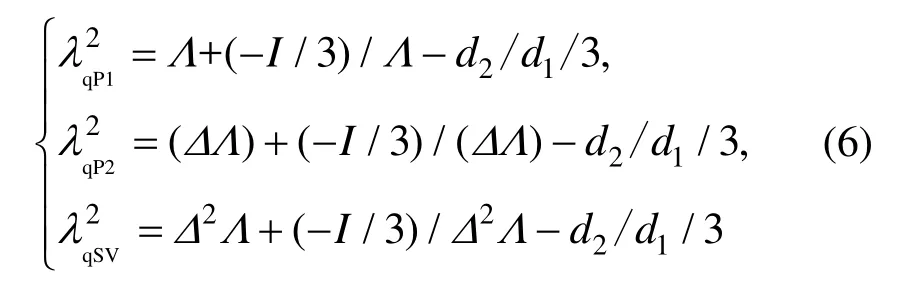
式中，Δ、Λ、І、d1及d2具体表达式见附录B。

将式(5)代入式(1)中，可得到平面内应力及孔压表达式如下：

1.2 层状TI饱和半空间平面内传递矩阵

如图1所示，结合式(5)以及式(7)并忽略e-ikx，可得第j层平面内部分位移、应力及孔压与上、下行波向量的关系如下：

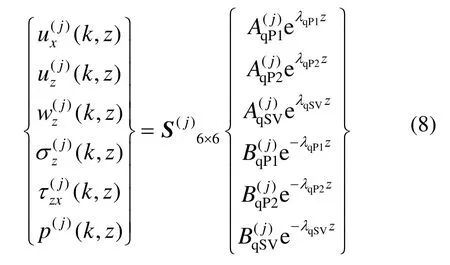
式中，S为系数矩阵，矩阵元素详见附录C。

如图2所示，在土层交界面处，应力、位移及孔压有以下连续条件：

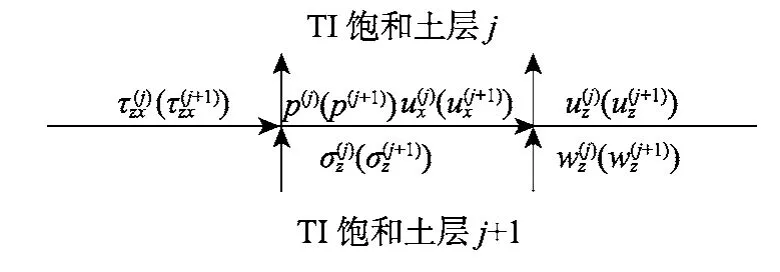
图2 TI饱和土层层间连续条件Fig.2 Continuity conditions between layers of TI saturated soil

将式(9)代入式(8)可得第j层上、下行波向量与第j+1层上、下行波向量的关系：

进一步变换式(10)并简化表达，可得第j层上、下行波向量幅值与第j+1层上、下行波向量幅值之间的关系：

式中，E(hj)(j)矩阵元素详见附录D。

由式(11)可得第j层上、下行波向量幅值与第j+1层上、下行波向量幅值之间的关系：

式中，T(j)=[S(j+1)]-1S(j)E(hj)(j)。

进一步，可以推得第N+1层上、下行波向量幅值与第1层上、下行波向量幅值之间的关系：

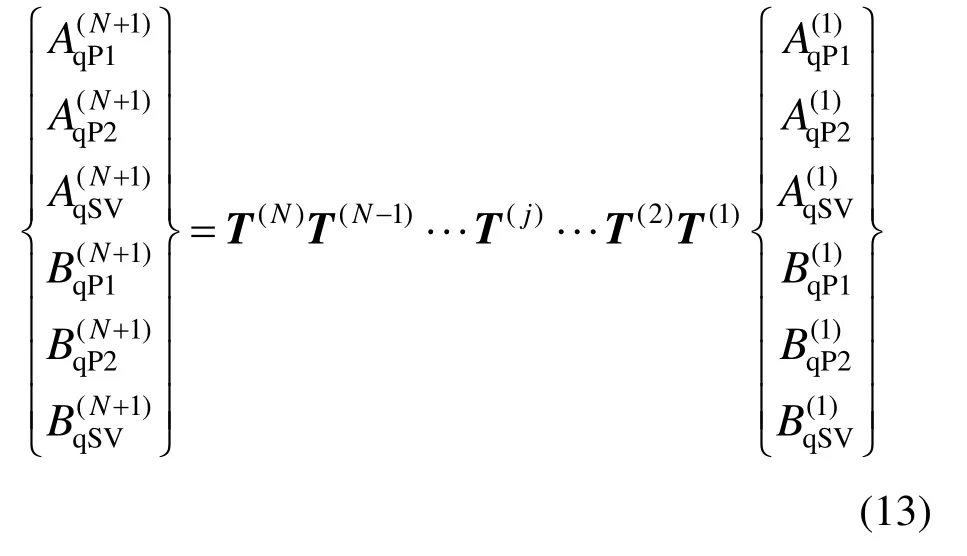
1.3 边界条件及地表动力响应

对于波在饱和层状半空间中传播问题的研究，由于传播介质为固液两相材料，建立边界条件时，不但要考虑土体的性质，还要考虑土体与孔隙流体的相互作用[24－25]。

假定半空间表面完全透水，边界条件可表示为：

假定半空间表面不透水时，边界条件可表示为：

分别将式(5)和式(7)代入透水边界条件和不透水边界条件，可得地表土层中入射波幅值与反射波幅值的关系：

式中：当边界透水时，M1~M9具体表达式见附录E；当边界不透水时；M1~M9具体表达式见附录F。

联立式(13)及式(16)，可求得地表处入射波及反射波幅值AqP1、AqP2、AqSV、BqP1、BqP2和BqSV，将其代入式(5)和式(7)可分别得到地表处位移及应力响应。

2 方法验证

为了验证本文频域结果的正确性，将退化结果与文献[26]结果进行比较。图3(a)和图3(b)分别给出了P波和SV波入射下各向同性弹性半空间中位移随深度的变化规律。计算参数取固体颗粒密度ρs=2000 kg•m-3，剪切模量G=2.0 GPa，泊松比v=0.33，阻尼比ζ=0.05，圆频率ω=100 rad/s，与孔隙流体相关的参数取为零。从图3可以看出，本文方法的结果与文献[27]结果吻合良好。其次，将TI饱和土层退化为TI弹性土层，与文献[27]计算结果进行比较。计算中，取土层厚度d=20 m，土层剪切模量Gh=26.7 MPa，Gv=13.3 MPa，基岩半空间剪切模量Gh=Gv=200 MPa，土层阻尼比取ζ=0.05，基岩阻尼比取ζ=0.02，密度均取ρs=ρR=2000 kg•m-3。从图4可以看出，本文结果与文献[27]结果一致，验证了本文方法的正确性。

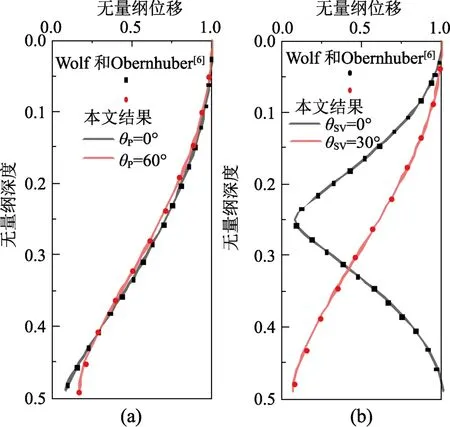
图3 各向同性半空间中位移幅值与深度的关系Fig.3 The relationship between displacement amplitude and depth in an isotropic half-space

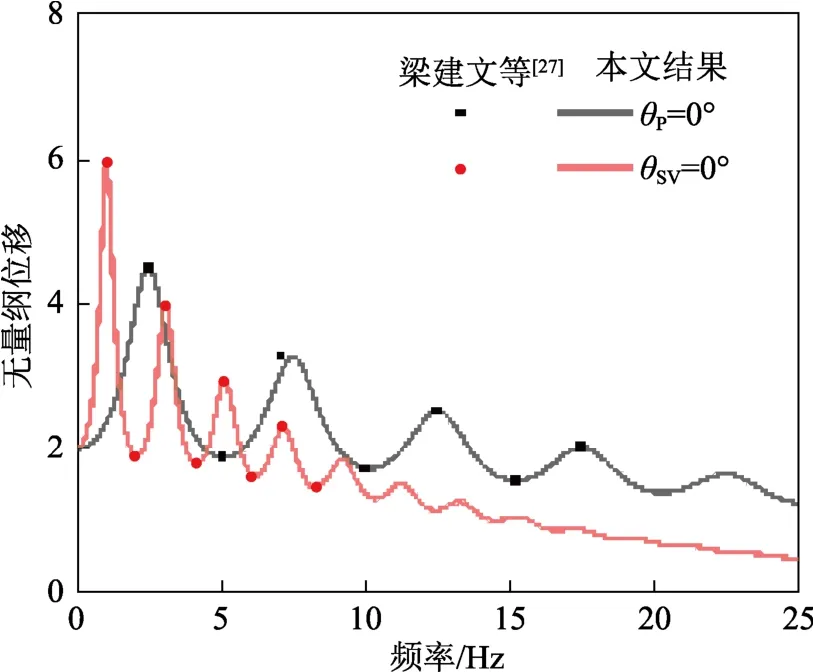
图4 层状TI场地地表位移幅值谱放大曲线Fig.4 Amplification curve of the surface displacement for the surface of a layered TI site

为了验证本文时域结果的正确性，将退化结果与EERA程序计算结果进行比较。以基岩半空间上单层各向同性场地为计算模型，计算参数取土层厚度d=10 m，土层剪切模量Gh=Gv=20 MPa，基岩半空间剪切模量Gh=Gv=200 MPa；密度均取ρs=ρR=2000 kg•m-3，阻尼比均取ζ=0.02。图5给出了 ElCentro波(0.1g)作用时场地地表的水平加速度时程曲线。从图5可以看出，结果吻合良好。其次，将TI饱和土层退化为TI弹性土层，与文献[27]计算结果进行比较。计算模型及计算参数取值为土层厚度d=100 m，土层剪切模量Gh=26.7 MPa，Gv=13.3 MPa，基岩半空间剪切模量Gh=Gv=200 MPa，土层阻尼比取ζ=0.05，基岩阻尼比取ζ=0.02，密度均取ρs=ρR=2000 kg•m-3。图6 给出了 El Centro 波(0.1g)作用时场地地表的加速度时程曲线。对比表明，两者结果一致，再次验证了本文方法的正确性。

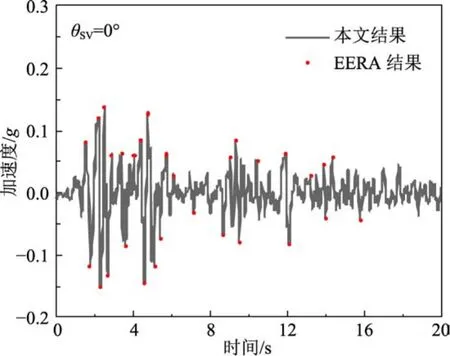
图5 层状各向同性场地地表加速度时程曲线Fig.5 Acceleration time-history curve for the surface of a layered isotropic site

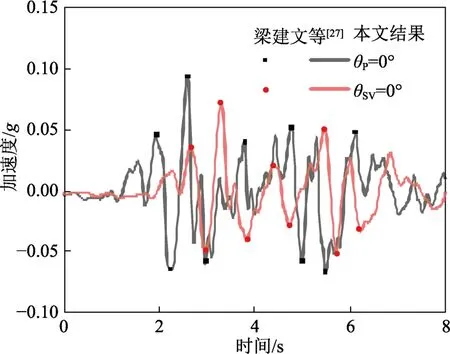
图6 层状TI场地地表加速度时程曲线Fig.6 Acceleration time-history curve for the surface of a layered TI site

3 算例和分析

算例模型为基岩上单一 TI饱和土层场地，研究了土体TI参数及饱和特性对场地自由场的影响，以归一化峰值为0.3g的CNTEWGXE地震波(2007年 8月 16日四川珙县地震长宁台记录，I0类基岩波)[28]作为输入地震动作用于露头处，获得了不同工况下场地地表的加速度时程曲线及其反应谱等动力响应结果。文中选取了3种具有不同模量比的TI饱和介质模型进行计算，具体参数见表1，其中，材料1为各向同性饱和介质。三种场地模型中，土层厚度d=60 m，阻尼比ζ=0.05，孔隙率ϕ=0.3。基岩半空间考虑为各向同性材料，剪切模量G=185 MPa，弹性模量Eh=Ev=462.5 MPa，阻尼比ζ=0.02，固体颗粒体积模量ks=1.8 GPa，其余参数与TI饱和土层参数相同。

图7和图8分别给出了qP1和qSV波以不同角度(θ=0°,30°,60°)入射时，层状 TI饱和场地地表的水平和竖向加速度时程曲线。从图中可以看出：

1)TI饱和场地与各向同性饱和场地地表的时程曲线存在一定差异。总体上，TI饱和场地(Gh/Gv=2.0和 3.0)的加速度峰值小于各向同性饱和场地(Gh/Gv=1.0)的加速度峰值。对于qP1波，TI饱和场地和各向同性饱和场地差异不大且波形相近；但对于qSV波，随着场地剪切模量比的增加，波的到时逐渐向右移动。这是由于土体的 TI性质改变了场地的动力特性及波在半空间中的传播速度，进而改变了加速度峰值及峰值时刻。

2)地震波垂直入射与斜入射时场地地表的时程曲线也有所不同，且主要体现在时程峰值方面。对于qP1波，其垂直入射下的竖向加速度峰值明显大于其斜入射下的峰值；对于qSV波，随着入射角的增加，峰值逐渐减小且土体 TI性质的影响逐渐减小。这主要是因为qP1和qSV波斜入射时，改变了波在水平和竖直两个方向的输入分量，同时，在土层交界面及地表处存在波型转换，进而改变了不同类型波的相互作用机制。

表1 TI饱和场地的材料参数Table 1 Material parameters for TI saturated site

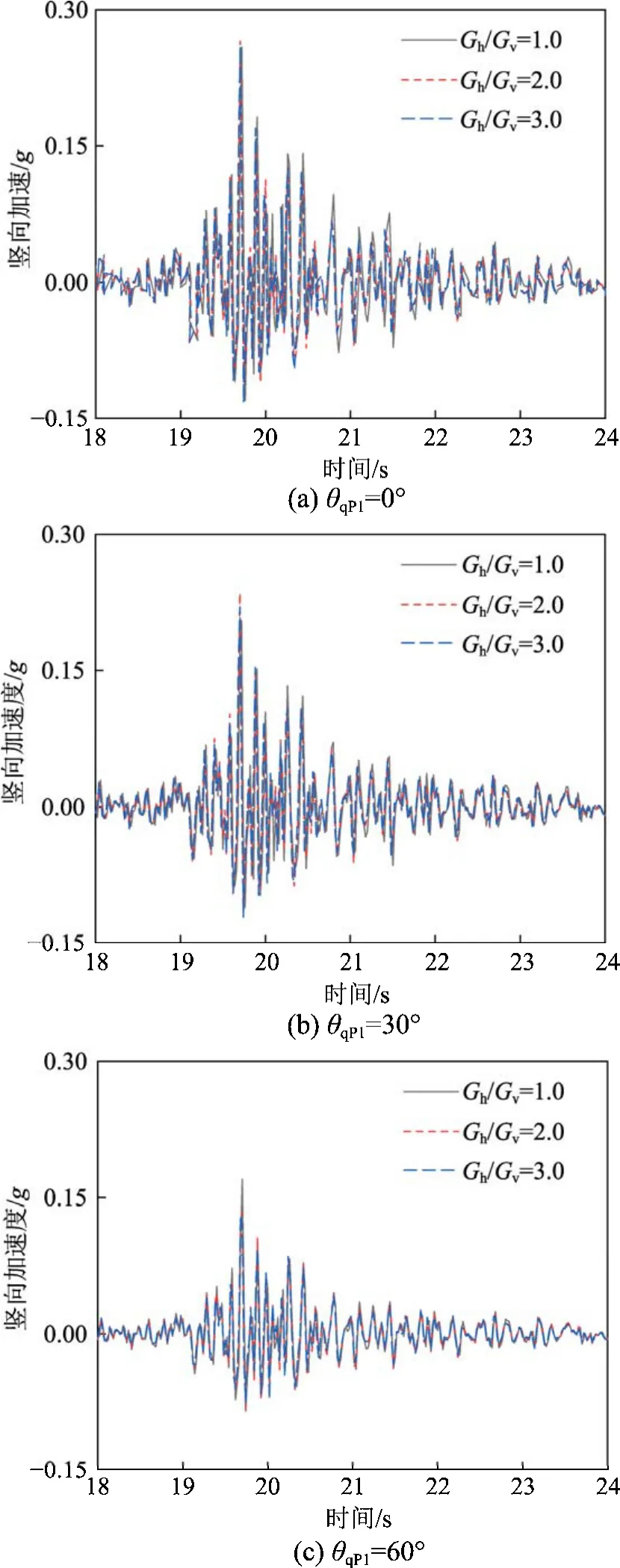
图7 qP1波入射下场地地表竖向加速度时程曲线Fig.7 Time-history curves of vertical acceleration for the surface under qP1 wave incidence

图9和图10进一步给出了相应的场地地表加速度反应谱。从图中可以看出：对于qP1波，TI饱和场地(Gh/Gv=2.0和 3.0)的反应谱幅值大于各向同性饱和场地(Gh/Gv=1.0)的反应谱幅值，且其在垂直入射下的幅值明显大于其斜入射下的幅值。对于 qSV波，随着Gh/Gv比值的增大，反应谱幅值逐渐减小；随着入射角度的增加，反应谱走势变得不再规律且其峰值变化不如qP1波显著。这是由于Gh/Gv比值的变化改变了场地的动力特性，不同TI参数场地对地震波产生了不同的滤波和放大效应，进而导致地表反应谱幅值及走势的改变。

图8 qSV波入射下场地地表水平加速度时程曲线Fig.8 Time-history curves of horizontal acceleration for the surface under qSV wave incidence

为研究场地饱和特性对场地地震响应的影响，给出了CNTEWGXE波(0.3g)作用在基岩露头处时，不同工况下场地地表的加速度时程曲线及其反应谱等动力响应结果。土层参数除渗透率k外取表1中材料1参数，基岩参数与上述算例取值一致。其中k1=k3=1000 m2表示不考虑两方向固液耦合作用(即粘滞性)，k1=k3=10-11m2表示考虑两方向固液耦合作用。

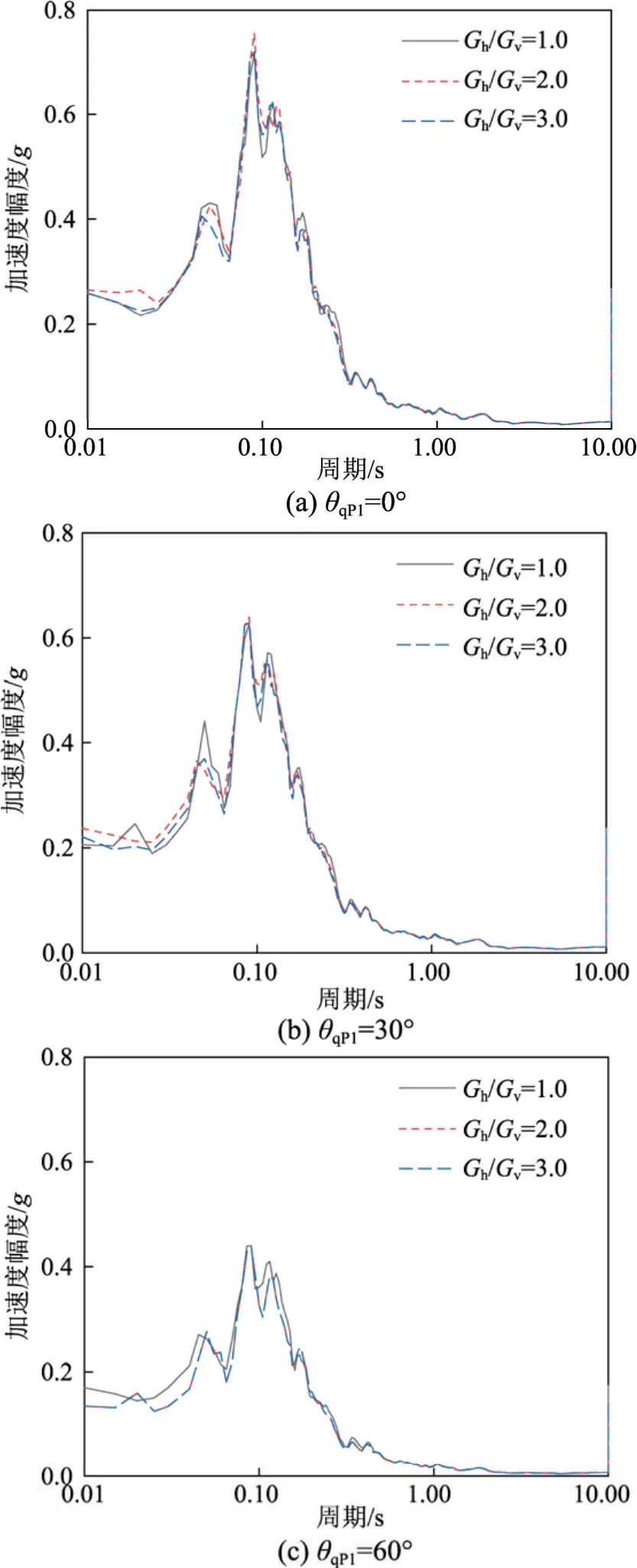
图9 qP1波入射下场地地表竖向加速度反应谱Fig.9 Response spectrum of vertical acceleration for the surface under qP1 wave incidence

图11和图12分别给出了qP1和qSV波以不同角度(θ=0°,30°,60°)入射时，层状 TI饱和场地地表的竖向和水平加速度时程曲线。从图中可以看出：对于qP1波，粘滞性对地表动力响应的影响很小，但在其垂直入射时的影响大于其斜入射时的影响；对于qSV波，粘滞性对地表动力响应影响显著，表现为考虑固液耦合作用时，地表动力响应明显减弱。这主要是因为波在饱和多孔介质中传播时，固液耦合作用所表现出的饱和多孔介质粘滞性会造成剪切波速的衰减及削弱[8]。

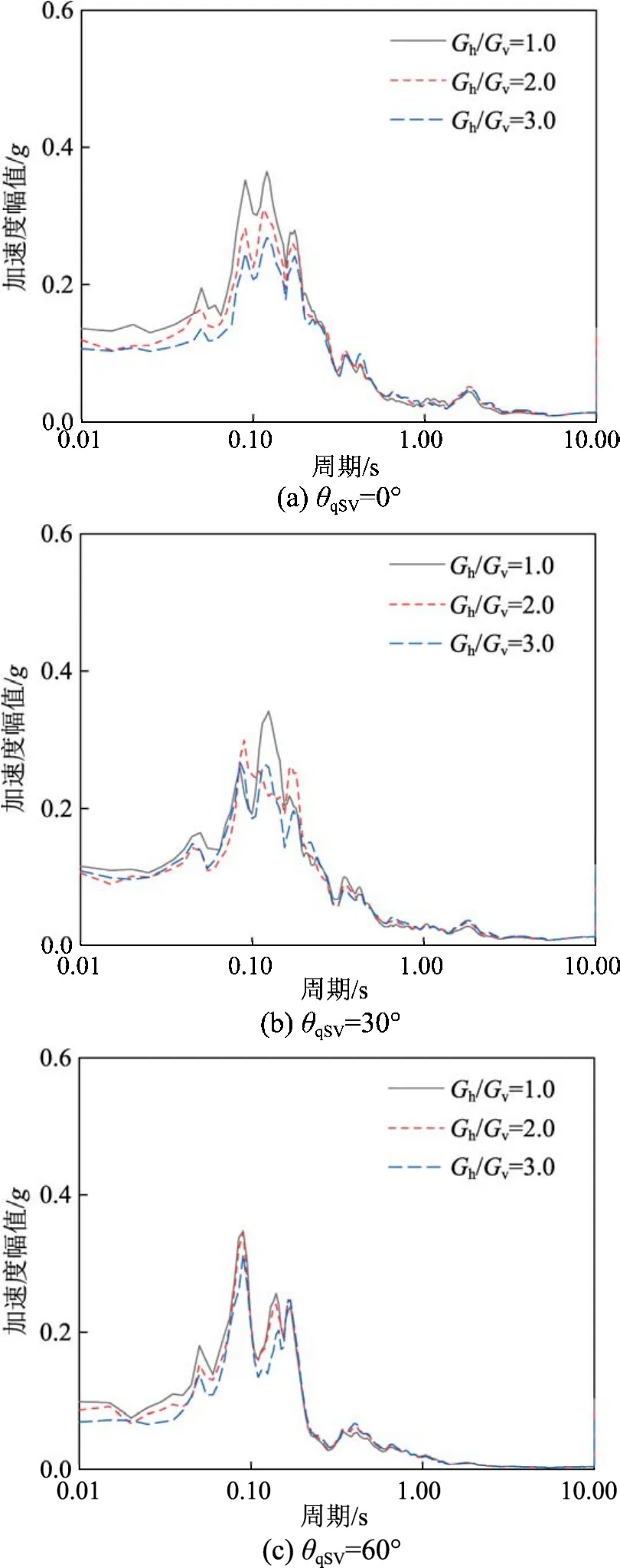
图10 qSV波入射下场地地表水平加速度反应谱Fig.10 Response spectrum of horizontal acceleration for the surface under qSV wave incidence

图13和图14进一步给出了相应的场地地表加速度反应谱。从图中可以看出，饱和多孔介质的固液耦合作用对于入射下的层状场地的动力响应具有削弱作用但未改变其峰值周期，且随着入射角度的逐渐增加，这种削弱作用逐渐减小。

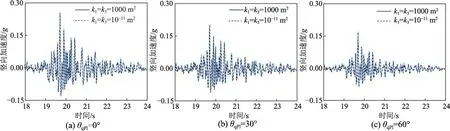
图11 qP1波入射下场地地表竖向加速度时程曲线Fig.11 Time-history curves of vertical acceleration for the surface under qP1 wave incidence

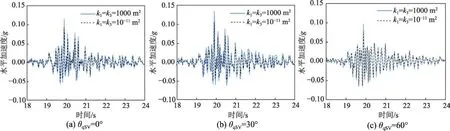
图12 qSV波入射下场地地表水平加速度时程曲线Fig.12 Time-history curves of horizontal acceleration for the surface under qSV wave incidence

图13 qP1波入射下场地地表竖向加速度反应谱Fig.13 Response spectrum of vertical acceleration for the surface under qP1 wave incidence

4 结论

本文采用传递矩阵方法求解了层状 TI饱和场地的地震动力响应，通过与已有文献进行对比验证了方法的正确性，进而进行了数值计算分析，研究了土体 TI参数及饱和特性对场地自由场响应的影响，得到以下主要结论：

(1)TI饱和场地与各向同性饱和场地地表的动力响应存在一定差异。总体上，TI饱和场地的加速度峰值小于各向同性饱和场地的加速度峰值，这一特性在qSV波入射下更为明显。随着Gh/Gv比值的增加，场地地表的反应谱峰值呈现减小的趋势，且场地的TI性质对qSV波的滤波作用更为明显。

(2)TI饱和场地的饱和特性对场地地表的动力响应存在重要影响且饱和特性对场地地表动力响应的影响主要体现在峰值方面。饱和多孔介质的固液耦合作用对波具有显著的削弱作用，这一特点在qSV波垂直入射时更为明显。

(3)地震波垂直入射与斜入射时场地地表的动力响应也有所不同。对于qP1波，其在垂直入射下的反应谱峰值大于其斜入射下的峰值；对于 qSV波，其在垂直入射和其斜入射下峰值变化并不显著但，但峰值周期有所变化。

附录A：

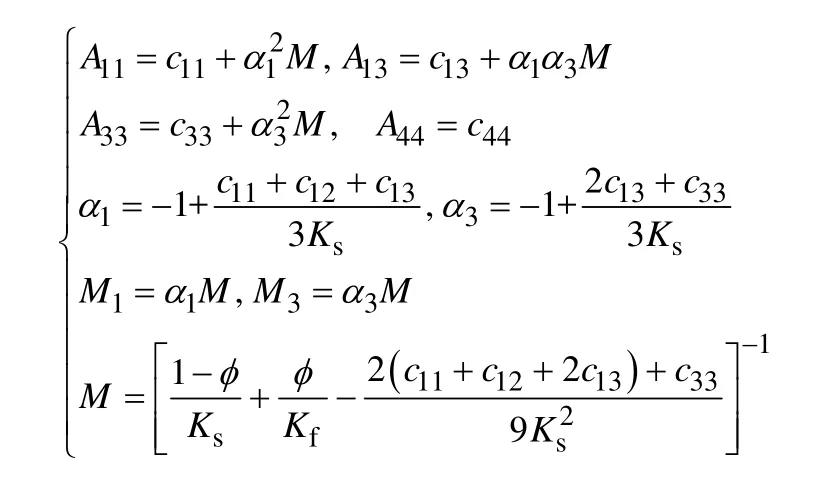
其中：

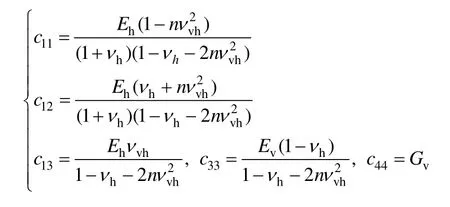
附录B：

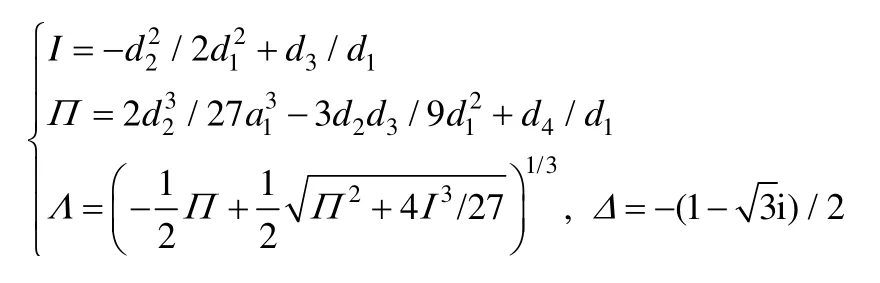
其中：

附录C：

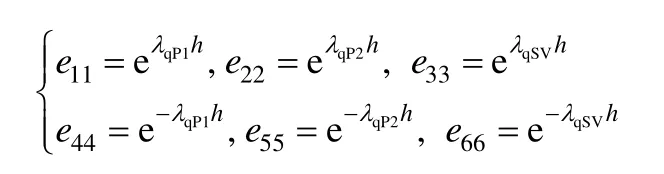
附录D：

附录E：

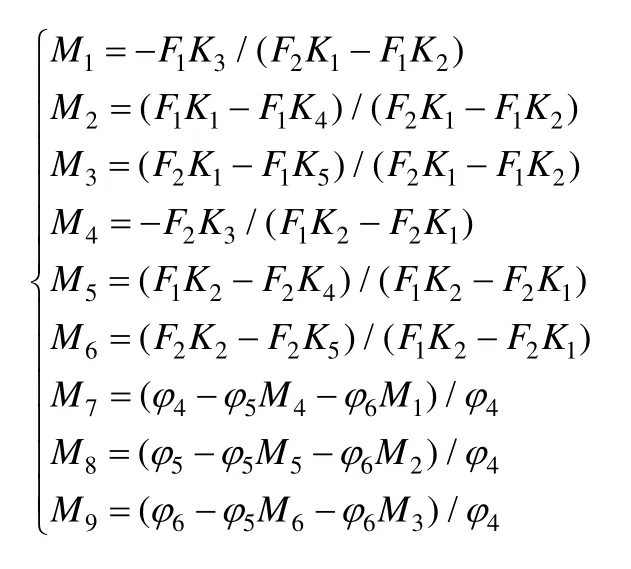
其中：

附录F：

其中：